HOW TO DEAL WITH SMALL OPEN READING FRAMES?
Małgorzata Wa
´
nczyk, Paweł Bła
˙
zej, Paweł Mackiewicz and Stanisław Cebrat
Department of Genomics, Faculty of Biotechnology, University of Wrocław, ul. Przybyszewskiego 63/77, Wrocław, Poland
Keywords:
Gene finding, Coding potential, Small ORFs, Short genes.
Abstract:
Current ’classical’ algorithms recognizing protein coding sequences do not work effectively with sequences
of small length. To deal with this problem we have proposed some improvements of the existing gene finders
without any assumed arbitrary threshold. Introduced parameters describe position of tested sequences in the
ranking of all small Open Reading Frames and short protein coding genes found in the analyzed genome. The
sequences can be ranked according to the coding potential calculated by ’standard’ gene prediction algorithms.
As an example, we used two algorithms for gene recognition and tested the set of selected small ORFs which
were selected from prokaryotic genomes using sequence similarity methods. The applied approach enabled to
identify promising sequence that can code for small proteins.
1 INTRODUCTION
The first step in the identification of protein coding
sequences in prokaryotic genomes is searching these
genomes for Open Reading Frame (ORFs), i.e. se-
quences beginning with a start translation codon and
ending at a stop translation codon. There are several
computer annotation tools which are able to evaluate
the coding potential of such sequences (see for re-
views (Azad, 2008), (Majoros, 2007)). For example,
the most common gene finding programs, which are
based on Markov chains, i.e. GeneMark (Borodovsky
and Mcinich, 1993), GeneMark.hmm (Borodovsky
and Lukashin, 1998), Glimmer (Delcher et al., 2007),
and EasyGene (Larsen and Krogh, 2003), recognize a
proper reading frame based on coding potential fac-
tors (a posteriori probabilities) computed for each of
six reading frames. These algorithms work generally
well for long ORFs (e.g. longer than 300 bp). Un-
fortunately, these methods become less reliable for
small Open Reading Frames (smORFs) - see also Fig.
1, Fig. 2 and Fig. 3. Because there are the enor-
mous number of short spurious ORFs found in every
genome, usually ORFs longer than 300 bp are con-
sidered and annotated. It allows to avoid many false
positives.
The output of the gene finding programs depends
also on the model parameters, for example the arbi-
trary threshold assumed on the coding potential level.
As a result of this, a lot of useful information is ’hid-
den’ from a user. For example coding potential for
alternative reading frames and ORFs with the subop-
timal coding probability are usually not given. The
lack of this information makes the gene finders in-
appropriate tool for the detection of smORFs which
usually have very weak coding potential. However,
the capabilities of these programs still can be used to
rank smORFs. Therefore, we have proposed an other
method using the gene finders to verify the coding ca-
pacity of short sequences. Our approach is based on
the measure of coding potential computed for a given
sequence without any assumed arbitrary threshold. In
the paper we have applied two algorithms for gene
recognition and assessed the coding potential of short
ORFs which were collected using other methods by
(Warren et al., 2010).
2 MATERIALS AND METHODS
In the analyses, we included 254 prokaryotic
genomes whose data were downloaded from Gen-
Bank (www.ncbi.nlm.nih.gov). All ORFs with anno-
tated function in these genomes were considered cod-
ing and were used as learning sets in the gene recogni-
tion algorithms. From the genomes we extracted the
set of all small ORFs of the length 30− 300 bp to eval-
uate efficiency of the applied methods. We also tested
the set of short ORFs found in intergenic regions by
(Warren et al., 2010). These frames escaped usually
from recognition by standard gene finding algorithms
but were identified by BLAST searches based on se-
246
Wa
´
nczyk M., Bła
˙
zej P., Mackiewicz P. and Cebrat S..
HOW TO DEAL WITH SMALL OPEN READING FRAMES?.
DOI: 10.5220/0003856202460250
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 246-250
ISBN: 978-989-8425-90-4
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

quence similarity within the selected set. Therefore,
according to the authors, we have referred to this set
as ’missing genes’ (’msg’). The authors listed 1153
such sequences. However, we excluded from this set
121 ORFs that had exactly the same nucleotide se-
quences. Finally, the analyzed non-redundant set in-
cluded 1032 ’msg’ sequences.
To calculate coding potential we applied PMC al-
gorithm (Bła
˙
zej et al., 2010), (Bła
˙
zej et al., 2011),
(Wa
´
nczyk et al., 2011) and constructed ’engine’ of
GeneMark (GM) (Borodovsky and Mcinich, 1993),
(Borodovsky and Lukashin, 1998). The PMC
algorithm considers six independent homogeneous
Markov chains to describe transition between nu-
cleotides for each of three codon positions in two
DNA strands separately. By the ’engine’ algorithm
we mean a typical GeneMark model that used three
periodic non-homogeneous Markov chain (model of
coding sequences) and homogeneous Markov chain
(model of non-coding sequences). The PMC and GM
algorithms were previously tested on many prokary-
otic genomes and achieved a good accuracy in the
recognition of protein coding sequences.
The decrease in prediction of shorter sequences as
coding (Fig. 1, Fig. 2 and Fig 3) indicates that this set
of sequences behaves in other way than longer ones.
Therefore it seems more appropriate to compare cod-
ing properties of smORFs with other short frames in-
stead of the longer ones. Then we proposed the fol-
lowing procedure for assessment of coding capacity
for smORFs in a given genome:
1. coding potential is computed for a tested set of
sequences as well as for short ORFs (30 − 300
bp) found in the genome including the set of short
ORFs annotated as coding;
2. the ORFs are arranged in the ascending order ac-
cording to their coding potential;
3. two parameters are calculated for a given tested
ORF:
• the frequency α
1
of all smORFs with the cod-
ing potential lower than the considered one (see
Fig. 4 for graphical interpretation);
• the frequency α
2
of all smORFs annotated in
genome with the coding potential lower than
the considered one (see Fig. 4 for graphical in-
terpretation).
3 RESULTS AND DISCUSSION
3.1 Relation between Coding Potential
and the Sequence Length
To depict the problem with gene recognition in the
dependence on their length we generated transition
probability matrices (describing transitions between
nucleotide states of the order h = 2) for Pseudomonas
putida NC 002947 protein coding genes in the same
way as in GeneMark algorithm. Next, using these
transition matrices, we generated 1000 random nu-
cleotide sequences of the length in the range of 30 −
600 bp with the increment of 3 bp. Finally, we run a
classification process using GeneMark ’engine’. As it
can be seen in Fig. 1, the fraction of sequences which
were recognized as coding is decreasing rapidly with
the sequence shortening from 300 bp. It is evident
that the efficiency of this method depends strongly on
the length of the analyzed sequence. It indicates that,
even if sequences are constructed acording to the ideal
model for protein coding genes, not all of them, espe-
cially shorter ones, are recognized as coding.
●
●
●
●●
●●
●
●
●●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●●
●●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●●
●●
●
●●
●
●
●
●
●●●●●
●
●●●●●●●●●●
●●
●
●
●●
●●
●●●●●●
●
●●●●●
●●
●●
●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
100 200 300 400 500 600
0.88 0.90 0.92 0.94 0.96 0.98 1.00
length [bp]
fraction
Figure 1: Fraction of sequences recognized as coding by
GeneMark ’engine’ in dependance on their length.
The compatible result is presented in Fig. 2 and
Fig 3 which shows that recognition of annotated short
protein genes as coding by PMC and GM algorithm
is less reliable than longer ones. 35% of the short
genes were classified in incorrect reading frames or
in non-coding sequences whereas only 4.9% longer
genes were misclassified. The corresponding values
obtained in GM algorithm are 39% and 4.3%, respec-
tively.
HOW TO DEAL WITH SMALL OPEN READING FRAMES?
247

Figure 2: Difference in classification efficiency of PMC al-
gorithm for long protein coding genes (over 300 bp) and
short protein coding genes (less than 300 bp) annotated in
Pseudomonas putida genome.
I II III IV V VI non−coding
long genes
short genes
frame of reading
frequency
0.0 0.2 0.4 0.6 0.8 1.0
Figure 3: Difference in classification efficiency of GM al-
gorithm for long protein coding genes (over 300 bp) and
short protein coding genes (less than 300 bp) annotated in
Pseudomonas putida genome.
3.2 Ranking of Small ORFs
Fig. 4 presents distributions of coding potential cal-
culated for annotated short protein coding genes and
all smORFs found in Pseudomonas putida genome
as an example. As expected, the coding potential of
these genes is usually higher than all smORFs which
represent mainly spurious non-coding ORFs. How-
ever, almost half of these genes show the potential
lower than 0.5 and they would be considered as non-
coding assuming the 0.5 threshold. It suggests that
the 0.5 threshold seems to be too restrictive for pro-
tein coding smORFs. On the other hand, only a low
fraction of these genes have the potential lower than
0.1, which, in turn, is typical of the false frames. The
application of parameters α
1
includes this informa-
tion about the relation of an analyzed sequence to the
whole set of all smORFs found in a given genome.
Similarly, α
2
considers the tested sequence among an-
notated short protein coding genes. The large value of
this parameter indicates that the analyzed ORF takes
a high position in the ranking and is likely coding.
a
1
a
2
annotated
0.0 0.2 0.4 0.6 0.8 1.0
0
2
4
6
8
coding potential
all
Figure 4: Graphical interpretation of α
1
and α
2
factors
and density functions of coding potential for all smORFs
and short protein coding genes annotated in Pseudomonas
putida genome calculated in PMC algorithm. The circle
represents a short sequence from the ’msg’ set character-
ized by α
1
= 0.70 and α
2
= 0.17.
These parameters were applied for the ’missing
gene’ set found by (Warren et al., 2010). As it was
shown in the previous section, we should not expect
high coding probabilities calculated in typical gene
recognition algorithms for sequences in this set be-
cause it consists only of smORFs. In fact, over 96%
and 87% of these sequences were classified to non-
coding or to one of alternative frames by GM algo-
rithm and PMC algorithm, respectively (Fig. 5). In-
terestingly, PMC algorithm proved slightly better and
classified some sequence to alternative frames. Nev-
ertheless, these algorithms can be used to make a
ranking of the tested ORFs and calculate for them α
parameters. There are no small genes annotated in
Pseudomonas putida genome at the end of the rank-
ing whereas some sequences from the ’msg’ set are
placed relatively high in the ranking (Fig. 6). These
’msg’ sequences posses quite high level of α
1
and low
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
248

Figure 5: Classification of sequences from ’msg’ set by
PMC and GM methods to six reading frames and non-
coding sequences.
Figure 6: Ranking made according to the coding poten-
tial calculated in PMC algorithm for different sets of ORFs
found in Pseudomonas putida genome.
level of α
2
although these values are slightly higher
for PMC than GM algorithm (Tab. 1). The relatively
high α values confirm high position of the tested se-
quences in the ranking and suggest that some of them
may be coding.
3.3 Analysis of α Parameters in All
Studied Genomes
The same analyses presented for Pseudomonas putida
genome were performed for each of 254 prokaryotic
genomes. Density functions of found α
1
parameter
Table 1: Comparison between α
1
and α
2
parameters com-
puted by PMC and GM algorithms for ’msg’ sequences
found in Pseudomonas putida genome.
coordinates PMC GM
left end right end α
1
α
2
α
1
α
2
741453 741581 0,77 0,06 0,74 0,02
741575 741730 0,70 0,02 0,57 0
741748 741578 0,71 0,03 0,72 0,01
1429534 1429644 0,80 0,07 0,76 0,02
1819786 1819917 0,77 0,06 0,76 0,02
2069197 2069307 0,80 0,07 0,76 0,02
3595887 3595756 0,77 0,06 0,76 0,01
4348783 4348953 0,71 0,07 0,72 0
4348956 4348801 0,70 0,02 0,57 0
4349060 4348950 0,80 0,07 0,76 0,02
for different types of sequences are shown in Fig. 7.
As expected, short annotated genes possess gener-
ally a narrow distribution shifted toward high α
1
val-
ues and show the peak around 0.9, which indicates
that majority of them are recognized with higher cod-
ing probabilities than all smORFs extracted from an-
alyzed genomes (Fig. 7). On the other hand, the gene
sequences read in alternative frames are characterized
by distribution skewed to lower α
1
values, which indi-
cates that many of them obtained relatively low values
in comparison to all smORFs. Interestingly, ORFs
from the ’msg’ set show distribution slightly shifted
to the gene distribution, with the peak around 0.6. It
suggest that substantial fraction of them can be cod-
ing.
a
1
Figure 7: Density functions of α
1
values computed by PMC
algorithm for annotated short ORFs, their alternative read-
nig frames, and ORFs belonging to ’msg’ set for all ana-
lyzed genomes.
HOW TO DEAL WITH SMALL OPEN READING FRAMES?
249

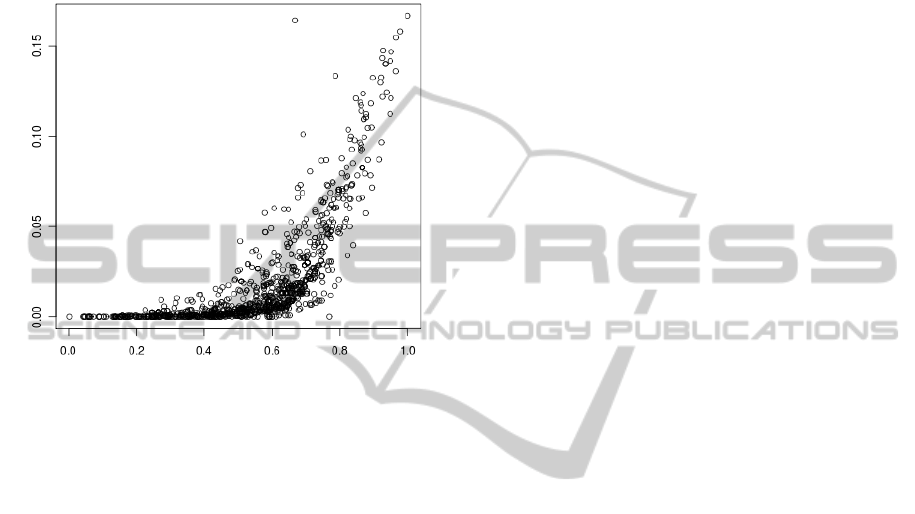
Fig. 8 presents a relationship between α
2
and α
1
calculated for sequences from ’msg’ set from all an-
alyzed genomes. It is clear that the increase in α
2
is
accompanied with the increase in α
1
for α
1
> 0.6. Se-
quences (especially those with high α values) which
probably code for proteins can be found in the subset
fulfilling the positive correlation.
a
1
a
2
Figure 8: Relationship between α
2
and α
1
calculated for
sequences from the ’msg’ set for all analyzed genomes.
4 CONCLUSIONS
The problem with recognition of short protein coding
sequences is still unsolved because ’classical’ algo-
rithms are less efficient for short sequences than for
longer ones. Therefore, every approach that could
improve this prediction is valuable. Here we have
proposed parameters that consider a tested sequence
in the ranking with all small ORFs and short protein
coding genes found in a given genome. This approach
can be used with every gene finding method that pro-
vides a coding potential factor. The recognition of
short genes is important because they may encode
peptides significant for cell functioning, e.g. fulfill-
ing various regulatory functions.
REFERENCES
Azad, R. K. (2008). Genes in prokaryotic genomes and their
computational prediction. College Press.
Bła
˙
zej, P., Mackiewicz, P., and Cebrat, S. (2010). Using the
genetic code wisdom for recognizing protein coding
sequences. In Proceedings of the 2010 International
Conference on Bioinformatics & Computational Biol-
ogy (BIOCOMP 2010), pages 302–305.
Bła
˙
zej, P., Mackiewicz, P., and Cebrat, S. (2011). Algo-
rithm for finding coding signal using homogeneous
markov chains independently for three codon posi-
tions. In Proceedings of the 2011 International Con-
ference on Bioinformatics and Computational Biology
(ICBCB 2011), pages 20–24.
Borodovsky, M. and Lukashin, A. (1998). Genemark.hmm:
new solutions for gene finding. Nucleic Acids Re-
search, 26(4):1107–1115.
Borodovsky, M. and Mcinich, J. (1993). Genmark: pararell
gene recognition for both DNA strands. Comput.
Chem., 17:123–133.
Delcher, A., Bratke, K., Powers, E., and Salzberg, S. (2007).
Identifying bacterial genes and endosymbiont DNA
with glimmer. Bioinformatics, 23(6):673–679.
Larsen, T. and Krogh, A. (2003). Easygene-a prokaryotic
gene finder that ranks orfs by statistical significance.
BMC Bioinformatics, page 4:21.
Majoros, W. (2007). Methods for Computational Gene Pre-
diction. Cambridge University Press, Cambridge, 1nd
edition.
Wa
´
nczyk, M., Bła
˙
zej, P., and Mackiewicz, P. (2011). Com-
parison of two algorithms based on markov chains ap-
plied in recognition of protein coding sequences in
prokaryotes. In Proceedings of the Seventeeth Na-
tional Conference on Applications of Mathematics in
Biology and Medicine, pages 118–123.
Warren, A., Archuleta, J., Feng, W., and Setubal, J.
(2010). Missing genes in the annotation of prokary-
otic genomes. BMC Bioinformatics, 11(131):12.
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
250