SURFACE-BASED SEGMENTATION OF 3D POINT CLOUD DATA

IN THE VECTOR FIELD REPRESENTATION

Van Tung Nguyen and Denis Laurendeau

Computer Vision and System Laboratory, Laval University, Quebec City, QC, Canada

Keywords:

3D Segmentation, Surface Modeling, Volumetric Representation.

Abstract:

In this paper, we propose an approach for 3D segmentation of point cloud data based on the vector ﬁeld

representation. A volumetric surface representation named the vector ﬁeld is ﬁrst computed for the input

point cloud. The data description in a voxel of the vector ﬁeld is then classiﬁed into eight surface types

by computing the sign of curvatures for the closest point of the voxel on the surface. A region-growing

sheme based on bivariate fuctions ﬁtting is ﬁnally applied to the closest points of these voxels for reﬁning the

segmented regions. This surface-based approach is entirely designed in the vector ﬁeld surface representation

and the advantages of using the vector ﬁeld are discussed. Experiments demonstrate the peformance of the

method.

1 INTRODUCTION

Segmentation is an essential step that can be found in

many research areas in computer vision such as shape

retrieval, compression, registration, and object recog-

nition. Basically, 3D segmentation consists of seg-

menting the input data into a set of meaningful “geo-

metric” parts or regions in the scene. Due to the im-

portance of this step in 3D applications, many seg-

mentation techniques have been developed that can

roughly be classiﬁed in two main categories: edge-

based and surface-based techniques (Hoover et al.,

1996)(Besl and Jain, 1988). In general, the former use

edge detection to create region boundaries (Hoover

et al., 1996)(Zhang et al., 2008) while the latter use

analytic surface description to divide the image into

disjoint regions (Besl and Jain, 1988)(Besl and Jain,

1986)(Zheng et al., 2008)(Gelfand and Guibas, 2004).

In this paper, a surface-based segmentation tech-

nique for 3D point cloud data is presented. Our goal is

to propose a segmentation technique that always min-

imizes computational load at every steps in the algo-

rithm by using the vector ﬁeld representation. The

vector ﬁeld representation, introduced in the next sec-

tions helps to reduce the complexity of neighbour-

hood operations often required by surface-based seg-

mentation approaches. Our approach ﬁrst computes

the vector ﬁeld from the input data. Then points be-

longing to regions with similiar geometric properties

are classiﬁed into eight types of surface geometry ba-

sed on local curvature properties computed from the

vector ﬁeld representation. A region growing scheme

based on the ﬁtting of low- order bivariate functions

is then performed on the initial set of regions to reﬁne

the segmentation.

The paper is organized as follows. First the vector

ﬁeld framework and curvature estimation approach

are presented in Section 2. Section 3 presents the

proposed segmentation technique including the ini-

tial region ﬁnding process and the reﬁnement process.

Next, experiments show the results demonstrating the

performance of the method. Section 5 discusses the

results and proposes future work.

2 CURVATURE ESTIMATION IN

THE VECTOR FIELD

REPRESENTATION

We ﬁrst introduce the terminology relevent to the vec-

tor ﬁeld surface representation computed for point-

set data and then extend the framework to introduce

a computational method for curvature estimation on

the vector ﬁeld.

2.1 The Vector Field Representation

In 3D modeling, representation of 3D data is a very

important issue since it has an impact on the compu-

157

Tung Nguyen V. and Laurendeau D..

SURFACE-BASED SEGMENTATION OF 3D POINT CLOUD DATA IN THE VECTOR FIELD REPRESENTATION.

DOI: 10.5220/0003857601570162

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 157-162

ISBN: 978-989-8565-02-0

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

tational complexity of the segmentation steps. Three

main 3D representation methods- mesh, volumetric

grids and polynomial representations- have been pro-

posed in the literature(Zheng et al., 2008)(Tubic et al.,

2002)(Zhang et al., 2008). Each type of representa-

tion has its advantages and disadvantages. In addition,

the chosen representation of the input data affects the

data segmentation and surface modelling steps sig-

niﬁcantly. In 2002, Tubic et al. (Tubic et al., 2002)

proposed a new implicit surface representation called

the “vector ﬁeld”. The vector ﬁeld framework has

demonstrated its capacity of unifying all steps of in-

terative 3D modeling (registration, integration, mod-

elling and visualization) in one type of data represen-

tation with linear computational complexity (Tubic

et al., 2004).

voxel

vector toward the

normal to the

closest point on

the surface

envelope

Point set

and surface

Figure 1: Vector ﬁeld representation.

In essence, the vector ﬁeld is a volumetric repre-

sentation where each voxel encodes the vector point-

ing from the voxel center to the closest point on the

surface to be modeled. Suppose that point cloud data

is available, the vector ﬁeld is built by updating the

covariance matrix C at each voxel located nearby data

point p

inside an envelope of size ε (Tubic et al.,

2002):

C =

∑

i=1

−

p)(p

−

∑

i=1

−p

(1)

where

p =

∑

i=1

and N the number of points that

have already participated in the voxel updates.

The eigenvector associated with the smallest

eigenvalue of the covariance matrix represents the

normal vector N to the tangent plane at the closest

point, then the direction of the vector ﬁeld F(v) at the

voxel v is computed as:

F(v) = N

p − v

(2)

where

is the scalar product.

Figure 1 shows a 2D view of a vector ﬁeld repre-

sentation, all the voxels within the envelope (bounded

by the dashed line) are updated with the information

of the point set on the surface (in black). The envelope

is used to determine the number of local voxels sur-

rounding the surface in which the vector ﬁeld is up-

dated for each incoming data point. The envelope size

and voxel size is always a trade-off. A large envelope

size or a small voxel size results in a dense vector ﬁeld

and increases the accuracy at the reconstruction step

but increases computational complexity and memory

requirements for storing the vector ﬁeld. Practically,

the envelope size is chosen twice the voxel size. As an

expansion to this basic deﬁnition of the vector ﬁeld,

we deﬁne two types of voxels: active voxels and sur-

face voxels. An active voxel is one that contains vec-

tor ﬁeld information pointing toward the closest point

on the surface (the voxels within the envelope in Fig-

ure 1). A surface voxel is an active voxel crossed by

the surface (for the point cloud data, that is an active

voxel contains the points on the surface). This con-

dition can be easily checked by ﬁnding whether or

not the closest point encoded by a surface voxel is lo-

cated inside this voxel (the surface voxels are colored

in red in the example on Figure 1). Given the exten-

sion, it will be shown next that only the curvatures at

the closest points of the surface voxels are computed

using the closest points of neighbouring active voxels

and only the closest points of the surface voxels con-

tribute to the estimation of the ﬁtting functions in the

segmentation process.

2.2 Curvature Estimation

Based on the vector ﬁeld framework described above,

we propose a scheme for estimating curvatures at the

closest point of each surface voxels (Nguyen and Lau-

rendeau, 2011). To do this, at a surface voxel, we de-

tect the closest point on the surface by the encoded

vector ﬁeld value then, the other closest points of

neighbouring active voxels are used to estimate the

curvature at this point. This approach based on the

vector ﬁeld departs signiﬁcantly from approaches that

compute curvature directly from the point cloud data.

As shown in Figure 2, to collect neighbouring points

of a given point p for estimating the curvatures, all

the points in the circle of radius r centered at p are

searched. In Figure 2.a, all points in the green re-

gion are obtained by the search. This search is hard to

achieve in a point cloud because nearest neighbours

must be found. However, in the vector ﬁeld represen-

tation, this search becomes an easy task by detecting

the neighbouring voxels, then collecting the closest

points of these active voxel that contribute to curva-

ture estimation because nearest information is stored

directly in the ﬁeld. In Figure 2.c, all neighbour vox-

els of a given voxel containing p are detected and

highlighted by light green colour, but only active vox-

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

158

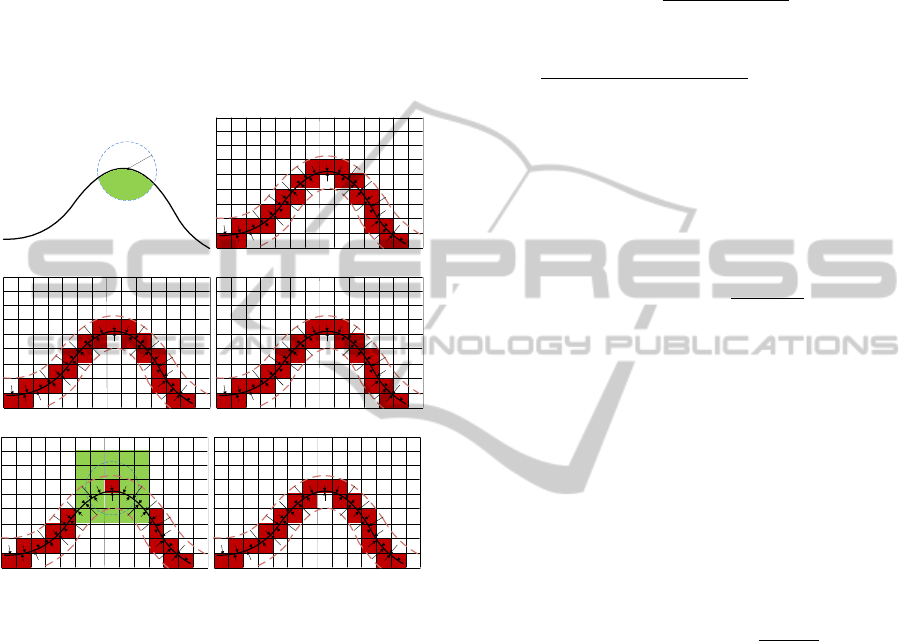
els are considered for the curvature estimation (light

green voxel in Figure 2.d). Changing the size of ra-

dius r to have more neighboring points in the search

is approximated by adding more layers of neighbour-

ing voxels in the curvature computation with the vec-

tor ﬁeld.(Figure 2.e and Figure 2.f show example of

two layers for detecting the neighbour voxels). Prac-

tically, the size of r or extention of more layers search

in the vector ﬁeld for collecting more neighboring

points is chosen suitable with the geometry of the

scene.

(a) (b)

(e) (f)

Figure 2: Illustration of neighbouring voxels detection for

cuvature computation using the vector ﬁeld. (a) shows the

search with point cloud directly, (b) is the encoded vec-

tor ﬁeld, (c) shows all the neighbouring voxels detected in

green for the center voxel in red and (d) shows the neigh-

bouring active voxels taken into account for curvature es-

timation, (e),(f) shows an example of the two voxel layers

search.

After detecting the neighbours to be considered

for curvature estimation, the method described by

Chen and Schmitt (1992) is used for estimating the

curvatures at a point using normal vectors and their

neighbouring points (Chen and Schmitt, 1992)(Dong,

2005). In our case, the normal vectors at the closest

points are implicitly encoded in the vector ﬁeld (as

shown in Figure 1) since the ﬁeld contains the direc-

tion of the closest point at the surface and Chen and

Schmitt’s method is exploited as follows.

Let us assume that a point p has m neighbours.

The main idea in this method is to choose a suitable

coordinate system (

) for a group of unit length

tangent vectors t on the local tangent plane at point p.

The normal vectors at that point and its neigbours are

used to estimate the normal curvatures k

) along

the tangent direction t

on the local tangent plane at p

as follows (Chen and Schmitt, 1992)(Dong, 2005):

) = −

− p,N

− N

− p,p

− p

(3)

− p) −

− p,N

− p) −

− p,N

(i=1,2..m) (4)

where

is the Euclidean norm of a vector and N

and N are normal vectors at p

and p. Suppose that

) is the maximum of the normal curvatures cor-

responding to the tangent direction t

. Then, the spe-

cial coordinate system (

) on the tangent plane at

p can be chosen as follows:

= t

× N

(5)

From this, a set of m equations is obtained according

to Chen and Schmitt’s method:

) = a cos

(θ

)+bcos(θ

)sin(θ

)+csin

(θ

) (6)

where θ

is the angle between t

and

(i=1,2..m).

A least-squares method is used for solving the set of

equations for the coefﬁcients a, b and c. This leads to

the Gaussian curvature(K), mean curvature (H) and

two principal curvatures k

1,2

as follows:

K = ac −b

/4, H = (a + c)/2, and

1,2

= H ±

− K (7)

3 SEGMENTATION IN THE

VECTOR FIELD

REPRESENTATION

As presented by Besl in 1988, using the sign of the

Gaussian and mean curvatures at points on a smooth

surface, the surface can be decomposed into a union

of simple surface patches that are approximated by bi-

variate polynomials with order lower than four (Besl

and Jain, 1986). In this section, we borrow Besl’s ap-

proach for segmenting surfaces based on the sign of

the curvatures and then use a region growing ﬁtting

process to reﬁne the initial segmentation. With some

assumptions, Besl’s approach is implemented in the

vector ﬁeld representation.

SURFACE-BASED SEGMENTATION OF 3D POINT CLOUD DATA IN THE VECTOR FIELD REPRESENTATION

159

3.1 Initial Segmentation with the Sign

of Curvatures

In section 2.2 we presented a method for estimating

the curvatures at the closest points of the surface vox-

els in the vector ﬁeld representation. Based on the

fact that surface characteristics are almost identical on

a small region surrounding a point, we use the clos-

est points as “prominent points” that characterize sur-

rounding regions occupied by the surface voxels. This

means that, based on the surface shape determined by

the curvature signs at a “prominent point” on the sur-

face, the region occupied by the corresponding sur-

face voxel belongs to the same surface type. Figure

3 shows the eight fundamental surface shapes possi-

ble based on the Gaussian and mean curvatures at a

prominent point (Besl and Jain, 1986).

Peak Surface

H<0, K>0

Flat Surface

H=0, K=0

Pit Surface

H>0, K>0

Ridge Surface

H<0, K=0

Minimal Surface

H=0, K<0

Saddle Ridge

H<0, K<0

Valley Surface

H>0, K=0

Saddle Valley

H>0, K<0

Figure 3: Eight fundamental surface types (Besl and Jain,

1986).

Therefore, in this initial segmentation step, the

surface is decomposed into small disjoint regions be-

longing to one of eight possible surface types by la-

beling surface types of “prominent point”. Figure 4

shows an example of how this initial segmentation is

obtained. A surface (Figure 4.a) is encoded by the

vector ﬁeld as shown in Figure 4.b. The surface voxels

with different colours express different shape types

(illustrated in Figure 3) of the “prominent point” of

these voxel respectively. Then the regions occupied

by these surface voxels have the same shape type (Fig-

ure 4.c). Figure 4.d shows the surface classiﬁed by

regions with different shape type expressed by differ-

ent colours. Section 4 will shows some typical results

obtained by the ﬁrst segmentation step.

3.2 Reﬁned Segmentation with Region

Growing

The region growing scheme is responsible for merg-

ing the coarse segmented regions obtained in the

above initial step to create larger surface patches. In

fact, it is the process of spreading out initial patches

from a seed region. As presented by Besl(Besl and

(a) (b)

Figure 4: Illustration of ideal results obtained from the ini-

tial segmentation. (a) is an example of input surface; (b) is

the vector ﬁeld with the surface types stored in the surface

voxels in different colours; (c) regions crossed by the voxels

have the same surface types; (d) regions in different colour

are obtained by the initial segmentation.

Jain, 1988), the curvature-sign primitives classiﬁed by

the initial step presented above can be approximated

well by a bivariate function with order lower than four

as illustrated next.

Suppose that a smooth surface is a twice-

differentiable function z=f(x,y). The form of the ﬁt-

ting function can be written as follows:

f (m,a;x,y) =

∑

i+ j≤m

i j

= a

+ a

x + a

y + a

xy + a

+ a

y + a

+ a

y + a

+ a

(8)

Where, m≤4 is the order of the function and the

function can be expressed for a planar, biquadratic,

bicubic and biquartic surface with the length of the

coefﬁcient vector a corresponding to 3, 6, 10 and

15. The surface ﬁtting function minimizes the least-

squares error metric

ε =

∑

i=1

(

f (m,a;x,y) − f (x,y))

(9)

Where N is the number of points contributing to the

estimation of the ﬁtting function. The region-growing

scheme based on this ﬁtting of functions in the vector

ﬁeld representation is as follows.

First, the surface shape types of the prominent

points set (the closest points of surface voxels) ob-

tained at the initial step are stored at the correspond-

ing surface voxels and coordinates of the prominent

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

160

points are extracted and stored in a list of set of promi-

nent points for the next processing step as shown in

Figure 5 (different colours of voxels are used for dif-

ferent shape types). This conﬁguration helps to avoid

checking all voxels to ﬁnd a surface voxel as a start-

ing point. Instead of checking all voxels to detect a

surface voxels, starting from a point in this list allows

to detect which surface voxel the point falls into.

List of

examined

prominent

points

A point in the

list and its

corresponding

voxel

Figure 5: Explanation of the conﬁguration for growing ﬁt-

ting in the vector ﬁeld.

Two key elements of a region growing process are

ﬁnding a starting seed point and deﬁning a stopping

criterion. For ﬁnding a good seed region, we start

with a prominent point in the list to detect to which

surface voxel it belongs to. Based on the detected

surface voxel, we consider its neighbouring surface

voxels to check whether or not these voxels are la-

beled with the same surface type. If it is the case, then

we have a “trustable” seed region to start the region

growing process with the closest points corresponding

to the surface voxels. The expansion process to ﬁnd

neighboring closest points for the surface ﬁtting pro-

cedure becomes easy by detecting neighboring sur-

face voxels (the same as shown in the Figure 2). When

a surface voxel is considered and its prominent point

has successfully contributed to the surface ﬁtting esti-

mation, it is assigned the label ’visited’ to avoid mul-

tiple scan for the corresponding closest point. For a

seed region, the stopping criterion is when the error

metric in the equation (9) is greater than a threshold

while the highest order of the bivariate function has

been reached (m=4). The idea of variable-order poly-

nomial ﬁtting proposed by Besl is used: each time a

seed region is chosen, we ﬁrst try to ﬁt with a plane to

the region (length of the coefﬁcent a is 3). If it is not

suitable (error metric is larger than the threshold), we

move to higher order surfaces (biquadratic, bicubic,

and biquartic surface, where a is 6, 10 and 15 respec-

tively). The overall decision to stop the ﬁtting process

of the region growing on the surface is to check if all

selected prominent points from the list fall into a ’vis-

ited’ surface voxel. This means that all regions on the

surface have been visited.

4 EXPERIMENTAL RESULTS

For validation, the proposed method is applied to

some popular testing objects. The envelope size of the

vector ﬁeld is always chosen as twice of voxel size,

and the size of voxel is chosen depending on resolu-

tion of object. To get the sign of Gaussian and Mean

curvatures, curvature is set to zero when it is smaller

than 0.4% of the maximum absolute value of curva-

ture. The threshold for the error in the ﬁtting process

is set to 0.5 of the voxel size.

For curvature estimation using the vector ﬁeld,

Figure 6 shows the colormap of Gaussian and Mean

curvatures estimated for the budda model. Colour

change corresponds to a change in minimum to max-

imum estimated value of the curvatures. The resolu-

tion of the budda model is good, so the estimated cur-

vature values are reliable given by the smooth change

in colours in the ﬁgure. With this model, the voxel

size is set 0.001.

(a) Gaussian curvature. (b) Mean curvature.

Figure 6: Colormap of estimated curvatures for the budda

model.

(a) (b)

(c)

Figure 7: Surface segmentation on a simple object. (a) view

of the surface of the surface object, (b) initial segmentation,

SURFACE-BASED SEGMENTATION OF 3D POINT CLOUD DATA IN THE VECTOR FIELD REPRESENTATION

161

Figure 7 shows the segmentation of a simple ob-

ject. Figure 7.b shows the result of the initial segmen-

tation. Surface regions of different surface types are

shown in different colours. The initial step includes

some fragmented regions caused by wrong estimated

curvature sign. Figure 7.c shows the improvement of

the result after applying the reﬁnement segmentation

process. Because the vector ﬁeld implicitly contains

reconstruction information, the algorithm for the re-

ﬁnement process is designed to reﬁne the shape type

of the surface to get segmented regions separated by

shape boundaries. The voxel size is set 0.18 for this

object.

(a) (b)

Figure 8: Surface segmentation on an object. (a) initial seg-

mentation, (b) reﬁned segmentation.

Figure 8.a shows the prominent points (closest

points on the surface of surface voxels) reconstructed

for another object after the initial segmentation step.

Different colours express different surface types of

the points. Figure 8.b shows the improved result com-

posed of reliable regions after the reﬁnement process.

Voxel size is set 0.065 for this object. The algorithm

is currently being improved to reduce the thickness of

boundaries on these objects.

5 CONCLUSIONS

A new mechanism for 3D segmentation was intro-

duced for point-set data in the vector ﬁeld surface

representation. An initial segmentation process is

ﬁrst proposed by segmenting the surface into disjoint

regions labeled by eight fundamental surface types.

Then the segmented regions are improved by a region

growing process based on bivariate function ﬁtting.

Designing the segmentation mechanism in the vec-

tor ﬁeld allows to keep computation simple and avoid

complex nearest neightbour search for curvature esti-

mation and spreading out in the region growing pro-

cess. Several directions are possible for future work.

For instance an adaptive scaling in computing local

features such as curvatures could help to avoid seed

region to be too fragmented. Robustness to noise will

also be investigated.

REFERENCES

Besl, P. J. and Jain, R. C. (1986). Invariant surface char-

acteristics for 3D object recognition in range images.

Computer Vision, Graphics, and Image Processing,

33:3380. ACM ID: 7056.

Besl, P. J. and Jain, R. C. (1988). Segmentation

through variable-order surface ﬁtting. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

10(2):167–192.

Chen, X. and Schmitt, F. (1992). Intrinsic surface prop-

erties from surface triangulation. In Proceedings of

the Second European Conference on Computer Vision,

ECCV ’92, pages 739–743, London, UK. Springer-

Verlag.

Dong, C. Wang, G. (2005). Curvatures estimation

on triangular mesh. Journal of Zhejiang Uni-

versity (SCIENCE), Journal of Zhejiang University

(SCIENCE):128–136.

Gelfand, N. and Guibas, L. J. (2004). Shape segmentation

using local slippage analysis. In Proceedings of the

2004 Eurographics/ACM SIGGRAPH symposium on

Geometry processing, SGP ’04, page 214223, New

York, NY, USA. ACM.

Hoover, A., Jean-baptiste, G., Jiang, X., Flynn, P. J., Bunke,

H., Goldgof, D., Bowyer, K., Eggert, D., Fitzgibbon,

A., and Fisher, R. (1996). An experimental compar-

ison of range image segmentation algorithms. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence.

Nguyen, V. and Laurendeau, D. (2011). A global regis-

tration method based on the vector ﬁeld representa-

tion. In 2011 Canadian Conference on Computer and

Robot Vision (CRV), pages 132–139. IEEE.

Tubic, D., Hebert, P., Deschenes, J., and Laurendeau, D.

(2004). A uniﬁed representation for interactive 3D

modeling. In 3D Data Processing, Visualization and

Transmission, 2004. 3DPVT 2004. Proceedings. 2nd

International Symposium on, page 175182.

Tubic, D., Hebert, P., and Laurendeau, D. (2002). A volu-

metric approach for the registration and integration of

range images: towards interactive modeling systems.

In Pattern Recognition, 2002. Proceedings. 16th In-

ternational Conference on, volume 3, pages 283–286

vol.3.

Zhang, X., Li, G., Xiong, Y., and He, F. (2008). 3D

mesh segmentation using mean-shifted curvature. In

Proceedings of the 5th international conference on

Advances in geometric modeling and processing,

GMP’08, page 465474, Berlin, Heidelberg. Springer-

Verlag.

Zheng, B., Takamatsu, J., and Ikeuchi, K. (2008). 3D model

segmentation and representation with implicit polyno-

mials. IEICE - Trans. Inf. Syst., E91-D(4):11491158.

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

162