HETEROGENEOUS ADABOOST WITH REAL-TIME

CONSTRAINTS

Application to the Detection of Pedestrians by Stereovision

ıc Jourdheuil

, Nicolas Allezard

, Thierry Chateau

and Thierry Chesnais

CEA, LIST, Laboratoire Vision et Ing

enierie des Contenus, Gif-sur-Yvette, France

LASMEA, UMR UBP-CNRS 6602, 24 Avenue des Landais, Aubiere, France

Keywords:

Adaboost, Stereovision, Real Time.

Abstract:

This paper presents a learning based method for pedestrians detection, combining appearance and depth map

descriptors. Recent works have presented the added value of this combination. We propose two contributions:

1) a comparative study of various depth descriptors including a fast descriptor based on average depth in a

sub-window of the tested area and 2) an adaptation of the Adaboost algorithm in order to handle heteroge-

neous descriptors in terms of computational cost. Our goal is to build a detector balancing detection rate and

execution time. We show the relevance of the proposed algorithm on real video data.

1 INTRODUCTION

The pedestrian classiﬁcation is one of the most re-

quested tools in the video surveillance ﬁeld. Some

speciﬁc solutions exist in the context of video ac-

quired with stationary cameras. In this case, im-

age features from the spatial and temporal domains

are fused in order to jointly learn the correlation be-

tween appearance and foreground information based

on background subtraction (Yoa and Odobez, 2008).

Some other works (Dalal et al., 2006), (Wojek et al.,

2009) have used the fusion of the appearance and

movement in the image in order to improve results.

The method described in this article can not use

these combinations because its implementation ﬁeld

is linked with the use of cameras embedded on mov-

ing vehicles. Issues linked with this class of appli-

cation are the reliability and the computing time of

the detector. During the last years, the community

has paid attention to depth map information coming

from sensors using stereovision (Walk et al., 2010),

(Enzweiler and Gavrila, 2011), (Ess et al., 2008),

in order to have an efﬁcient classiﬁcation. We will

present some of these descriptors and their perfor-

mances when they are used by an Adaboost learning

algorithm.

Works (Walk et al., 2010) combining both appear-

ance and disparity descriptors have been also pub-

lished recently. However, the fusion of several descr-

iptors often increases the processing time. In addi-

tion, this difference of computation time is never in-

cluded in the learning phase of the detector while the

objectives of the application are to achieve a real-time

solution. We propose a modiﬁcation of Adaboost al-

gorithm by introducing a penalty linked with algorith-

mic complexity of each descriptor.

In a ﬁrst part, we present different weak classi-

ﬁers based on depth information. Then we compare

them with the Histogram of Oriented Gradient (HOG)

method based on the image luminance. In a second

part, we will present an innovative learning method,

called Heterogeneous Adaboost (HAB), designed to

merge several detectors, by taking into account the

computing time of each algorithm.

2 DEPTH DESCRIPTORS

In this ﬁrst section four descriptors of the depth map

are presented. The ﬁrst three are based on local devia-

tions of depth. The last one is calculated on the depth

itself.

In the Figure 1, the left image shows a pedestrian

moving in an industrial environment. The pseudo im-

age on the right of the ﬁgure shows the representation

of the associated depth map.

The Figure 2 shows, in its upper part, a set of

depth maps for pedestrians (positive examples)and its

539

Jourdheuil L., Allezard N., Chateau T. and Chesnais T..

HETEROGENEOUS ADABOOST WITH REAL-TIME CONSTRAINTS - Application to the Detection of Pedestrians by Stereovision.

DOI: 10.5220/0003858305390546

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 539-546

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Example image (left) and the associated depth

map (right).

lower part examples of depth maps of the environment

(negative examples). The creation of this map is made

by a conventional method for dense depth map in real

time, not presented in this article.

Figure 2: Positive examples (upper) and negative examples

(lower) in the depth map.

A sliding window strategy (with a ratio of width

to height equals

) covering the ground level, is used

to scan the depth image ( Figure 3). For each window,

a feature vector composed a of set of local descriptors

from the depth map, is computed. Then vectors are

evaluated following a model created during off-line

learning stage.

Figure 3: Evaluation scheme of pedestrian classiﬁcation.

2.1 Comparison of Descriptors

The use of depth map-based descriptors is recent. We

have adapted well-known efﬁcient descriptors of ap-

pearance to be used on the depth map. We have also

created a speciﬁc descriptor of the depth map. We

present four depth map descriptors with HOG as a ref-

erence method on real images.

2.1.1 HOG-depth

This descriptor describes the depth map with as a His-

togram of Oriented Gradient (HOG) of depth. This

descriptor type is typically used to represent images

in appearance (Dalal and Triggs, 2005) generally. The

version used for the study, has been enriched with

the gradient magnitude, (Begard et al., 2008): a nor-

malized histogram of nine magnitudes of orientation

(from 0

◦

to 180

◦

) is built from the map of depth gra-

dient. Then this histogram is enriched with a tenth

value: the gradient magnitude.

2.1.2 Covariance Matrix (MatCov)

This descriptor, derived from the work of Tuzel (Tuzel

et al., 2008) offers a pedestrian coding from the co-

variance matrices of appearance and its spatial deriva-

tive, calculated on sub-windows of the scan. Our

proposition is the same as the previous one but using

information from the depth map with the data [x y d]

where x and y are the coordinates of pixel and d the

depth value of this pixel. Then the covariance matrix

is in a connected Riemannian manifold M

3×3

cov

: χ → M

3×3

(1)

Where M

3×3

is in R

3×3

. A function ψ : M

3×3

→ R

projects the manifold to the tangent space using the

formula:

ψ(X) = vec

(log

(X)) (2)

Where X and µ are two symmetric positive matrices.

With:

vec

(X) = upper(µ

−

Xµ

−

) (3)

And :

log

(X) = µ

log(µ

−

Xµ

−

)µ

(4)

µ is the point of the weighted average of the covari-

ance matrices, coming from the formula:

µ = arg min

Y ∈M

3×3

∑

i=1

,Y ) (5)

So an essential metric for the comparison of the two

covariance matrices is deﬁned.

2.1.3 Covariance, Depth Variance (CovVar)

The previous descriptor (MatCov) has the drawback

of being quite heavy in terms of computation time.

So one simpliﬁed version, consisting of the deﬁnition

of a distance which does not take any more account of

the properties of the Riemannian manifold, has been

used. In the covariance matrix 3 ∗ 3 created with the

data [x y d], the two ﬁrst columns are constant. Thus,

the matrix is reduced to its last column and we get the

vector [cov(x, d) cov(y, d) var(d)]. So the norm L2

to deﬁne the distance between two descriptors can be

used by this reduction.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

540

2.1.4 Average

We propose a simple descriptor based on the average

of the differences between the test depth d and mea-

sured depth z in a sub-area of the window of analysis.

This descriptor called M

is associated with the re-

gion r

, and it is deﬁned by the following equation:

∗

∑

d∈r



z − d if z deﬁned

0 if z undeﬁned

(6)

Where n is the number of deﬁned depth points z. The

sizes and positions of regions r

are deﬁned during the

learning phase.

This average depth-based descriptor may remem-

ber the descriptor DispStat (Walk et al., 2010) using a

ﬁxed cutting up of the disparity map.

2.2 Performance Comparison

The performance comparison of the different descrip-

tors was done by using a learning machine type Adap-

tive Boosting algorithm (Freund and Schapire, 1999)

and a decision stump classiﬁer type for HOG-depth,

CovVar, Average, and HOG on appearance. In the

case of a learning phase with MatCov, the weak clas-

siﬁer is a linear regression done on the components of

symmetric matrices.

2.2.1 Assessment Protocol

Learning has been done on a video shot inside a ware-

house where 10, 000 images of negative examples and

1, 500 images of positive examples have been ex-

tracted. Each tested area R is divided into 1, 482 rect-

angular regions r

In boosting methods, a new weak classiﬁer is cho-

sen at each round of learning. Then the n chosen

weak classiﬁers are combined in a new strong classi-

ﬁer. Each strong classiﬁer is evaluated on 10, 000 im-

ages of negative examples and 1, 500 images of posi-

tive examples taken from a test video shot in a differ-

ent warehouse of this one the learning one. Following

tests done, the maximum of performance on the test

database can be achieved through a strong classiﬁer,

created after the one which has reduced the learning

error to 0 in the learning phase. As about 100 rounds

of Adaboost are required by classiﬁers to reduce the

learning error to 0 on the learning database, we have

chosen to execute 300 rounds on the learning database

to maximize the probability of regulation of the max-

imum performance on the test database. The 300

Receiver Operating Characteristic (ROC) associated

with each classiﬁer are compared and the best curve

is selected, according to the criterion:

Best = arg

300

max

t=1

Sur f ace(Curve

) (7)

Thus, each classiﬁer type can be evaluated at its maxi-

mum performance regardless of the number of rounds

completed. A similar test of the HOG descriptor on

the appearance will be the reference curve.

2.2.2 Results

The ﬁgure shows ROC curves obtained by using the

previous protocol. The curves have been compared at

a detection rate of 90% to the reference HOG curve

(red). HOG-Depth curve (green) has a false positive

rate of 15% or 11% above the baseline (4%). Strong

classiﬁers selected of curves HOG-Depth and HOG

have been learned with a respective number of rounds

of 270 and 290. The false positive rate of the curve

MatCov (purple) is 8% (120 rounds), the curve Cov-

Var (dark blue) is 10% (208 rounds), respectively 4%

and 6% higher than the reference. The percentage of

false positive of the Average curve (light blue) is close

to 4% (212 rounds) similar to the reference.

Figure 4: Comparison of detection performance of weak

classiﬁers on the depth map (HOG is the reference).

The results obtained using our Average classiﬁer

created speciﬁcally to work on the depth map are as

good as the ones obtained using HOG appearance.

That conﬁrms our initial hypothesis: the depth map

is sufﬁcient to classify pedestrians. These encourag-

ing results, on the use of the depth map for the pedes-

trian classiﬁcation, open a new way of merger with a

appearance descriptor.

HETEROGENEOUS ADABOOST WITH REAL-TIME CONSTRAINTS - Application to the Detection of Pedestrians by

Stereovision

541

3 HETEROGENEOUS

ADABOOST

The work (Walk et al., 2010) of Walker et al. has

shown that the fusion of descriptors of appearance,

motion and disparity improves signiﬁcantly the clas-

siﬁcation results. However, this one generates an in-

crease in computing time which can be a limited fac-

tor not acceptable for real-time application.

In this second part, we propose to take account of

a constraint of algorithms cost, softened by α ∈ [0, 1],

in the Adaboost algorithm (Friedman et al., 1998)

(Heterogeneous Adaboost , HAB). It will be selec-

tion criteria of heterogeneous descriptors to create a

strong and fast classiﬁer. Also, the depth descriptors

presented in the previous section, will be combined

with HOG appearance in a global learning phase.

Following the results of the previous study, the

method CovVar will be preferred to MatCov method

because the change of the method MatCov by CovVar

method damages a little bit results while reducing the

computation time.

3.1 Algorithm HAB

Let C be the set of weak learning algorithms to Ad-

aboost. We deﬁne an algorithm as a component de-

scriptors. We associate to each algorithm, its algorith-

mic cost λ

. The algorithmic cost can be estimated

from the complexity of the descriptor, or measured

statistically on a target machine.

One algorithmic cost softened normalized

, en-

abling management of the inﬂuence of algorithmic

cost in the calculation of the pseudo error penalized,

is calculated using the equation:

∑

c=1,..,C

(8)

where α ∈ [0; 1] is a softening coefﬁcient choosen

empirically.

In the classical AdaBoost, the criterion to mini-

mize is calculated as follows:

= E[e

−y

] (9)

With

: x → {−1;1} the response of the weak

classiﬁer. We propose to penalize the criterion to min-

imize ε

by the algorithmic cost

in HAB. So the

new equation of the criterion to minimize (penalized)

becomes:

E[e

−y

] (10)

When one component of a descriptor is chosen by

the algorithm, other ones related components of the

same descriptor are calculated simultaneously. There-

fore, the algorithmic cost λ

of all components of de-

scriptors already calculated change and should be up-

dated. So we introduced the algorithmic cost λ

classiﬁcation without calculation.

For each component c already calculated, λ

is re-

placed by the algorithmic cost empty λ

. The new

normalized softened algorithmic cost

is recalcu-

lated.

Algorithm 1 on page 5 describes the different

stages of Heterogeneous Adaboost.

3.2 Algorithmic Cost

The evaluation of the complexity of the descriptor and

the statistical measure of processing time on a target

machine are among the possibilities to estimate the al-

gorithmic cost λ

of weak classiﬁers c ∈ C. We chose

to measure the average time (ns) of calculation re-

quired to calculate a weak classiﬁer. The ﬁgure 5 rep-

resents the algorithmic cost

for each method CovVar,

HOG, HOG-depth and Average, and the algorithmic

cost (called empty) cited in the HAB algorithm, eval-

uated by a classiﬁer that returns an empty vector.

Figure 5: Algorithmic cost λ

for each method Cov-

Var, HOG, HOG-depth and Average and empty cases in

nanoseconds (ns) per weak classiﬁer.

The algorithmic cost varies from 1, 100ns for Cov-

Var to 31ns for the Average classiﬁer which is close

to 22.5ns of the classiﬁer empty. This classiﬁer is

also four times faster than the reference HOG and its

derivative HOG-Depth (130ns).

We deﬁne the algorithmic cost Λ

of the strong

classiﬁer output of the rounds t of HAB following

All tests were performed on a PC computer equipped

with a 2.8GHz processor.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

542

Algorithm 1: Heterogeneous Adaboost.

Require: N a set of labelled examples {(x

, y

)}

n=1,..,N

, D a probability distribution associated with N exam-

ples, C a set of learning algorithms with low computational cost associated {(WeakLearn

, λ

)}

c=1,..,C

, λ

algorithmic cost of empty, α ∈ [0;1] a coefﬁcient of mitigations, T a number of iterations.

1: The weight vector w

= D(i) pour i = 1, .., N

2: A vector of normalized costs

∑

c=1,..,C

3: The initial error ε

= 0, 5

4: for t = 1 to T do

∑

i=1

6: for c = 1 to C do

7: Call the weak classiﬁer learner WeakLearn

with the distribution w

that returns a weak classiﬁer

(y=1|x)

(y=−1|x)

of algorithmic cost λ

8: Calculate the penalized criterion to minimize

E[e

−y

]

9: end for

10: Select the weak classiﬁer that minimizes the penalized criterion to minimize:

ˆc

| ˆc = arg min

c=1,..,C

11: Update the weight vector

t+1

= w

−y

)

12: Update of the new algorithmic cost λ

= λ

for all c calculated at the same time ˆc.

13: Normalization of the cost

∑

c=1,..,C

with α ∈ [0; 1]

14: end for

15: return the strong classiﬁer:

H(x) = sign

∑

t=1

(x)

equation:

= Λ

t−1

+ λ

(11)

where λ

is the algorithmic cost of the weak classiﬁer

selected round t.

3.3 Choice of the Softening Coefﬁcient

The magnitude of the algorithmic cost

greatly in-

ﬂuenced the choice of the weak classiﬁer in the HAB

algorithm. To manage this inﬂuence, a softening coef-

ﬁcient α is applied (equation 8). The latter is chosen

accordingly to the learning error and the computing

time Λ

In this section, we will present the inﬂuence

and the choice of a coefﬁcient α for HAB with

HOG+Average descriptor.

3.3.1 Learning Error

The AdaBoost algorithm minimizes the learning error

for each of his rounds. The ﬁgure 6 shows the learning

error ε

based on the number of rounds t for classical

Adaboost (red) and the HAB algorithm (blue). As

we can see, the learning error of Adaboost is less the

HAB error.

In the ﬁgure 7, we represented the learning error

based on the algorithmic cost of strong classiﬁers Λ

(equation 11) to account for the algorithmic cost. In

this case, algorithm HAB (blue) reduces the learning

error faster than classical Adaboost (red) regardless of

the algorithmic cost (Time).

HETEROGENEOUS ADABOOST WITH REAL-TIME CONSTRAINTS - Application to the Detection of Pedestrians by

Stereovision

543

Figure 6: Learning error based on the number of rounds for

HOG+Average learning with classical Adaboost and HAB.

Figure 7: Learning error based on the number of comput-

ing time (ms) for learning HOG+Average with classical Ad-

aboost and HAB.

3.3.2 Determination of the Coefﬁcient α

The experiments have showed that the algorithmic

cost inﬂuences strongly the selection of weak clas-

siﬁers. We have looked for to manage its inﬂuence

by assigning a softening coefﬁcient α (equation 8) to

it. The ﬁgure 8 shows the learning error based on the

algorithmic cost (time) for a representative sample of

possible values α ∈ {0; 0.06;0.12;0.25; 0.50; 1}. In

this ﬁgure, the curve α

(black) represents the learn-

ing error without softening coefﬁcient. The percent-

age error of the learning curve has reached only 5%

error at the end of 300 rounds of learning. The curve

(dark blue) represents the evolution of the learning

error without algorithmic cost (softening maximum,

similar to a classical AdaBoost). The other curves

are related to values of the coefﬁcient α ∈ [0; 1]. The

value of this coefﬁcient has a very signiﬁcant effect

on the performance of the algorithm. Curve α

0.12

(green) appears to be a good compromise between the

decrease of the learning error and computing time.

Figure 8: Learning error for HOG+Average

method based computation time (ms) for

α ∈ {0;0.06; 0.12; 0.25; 0.50; 1}.

To verify the effectiveness of the curve α

0.12

we used the data of the areas of ROC curves of

the protocol section 2.2.1 (page 3) that we posted

on a algorithmic cost Λ

. The ﬁgure 9 shows the

1-surface of the ROC curves as a function of time for

α ∈ {0; 0.06;0.12;0.25; 0.50; 1}.

It conﬁrms the performance of the curve α

0.12

(green).

Figure 9: 1-surface curves ROC for HOG+Average

method based computation time (ms) for

α ∈ {0;0.06; 0.12; 0.25; 0.50; 1}.

3.4 Fixed Computation Time

This section presents the experiments conducted on

the test dataset, to compare method performance

with those of HAB on the three classical Adaboost

weak classiﬁers HOG+Average, HOG+CovVar et

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

544

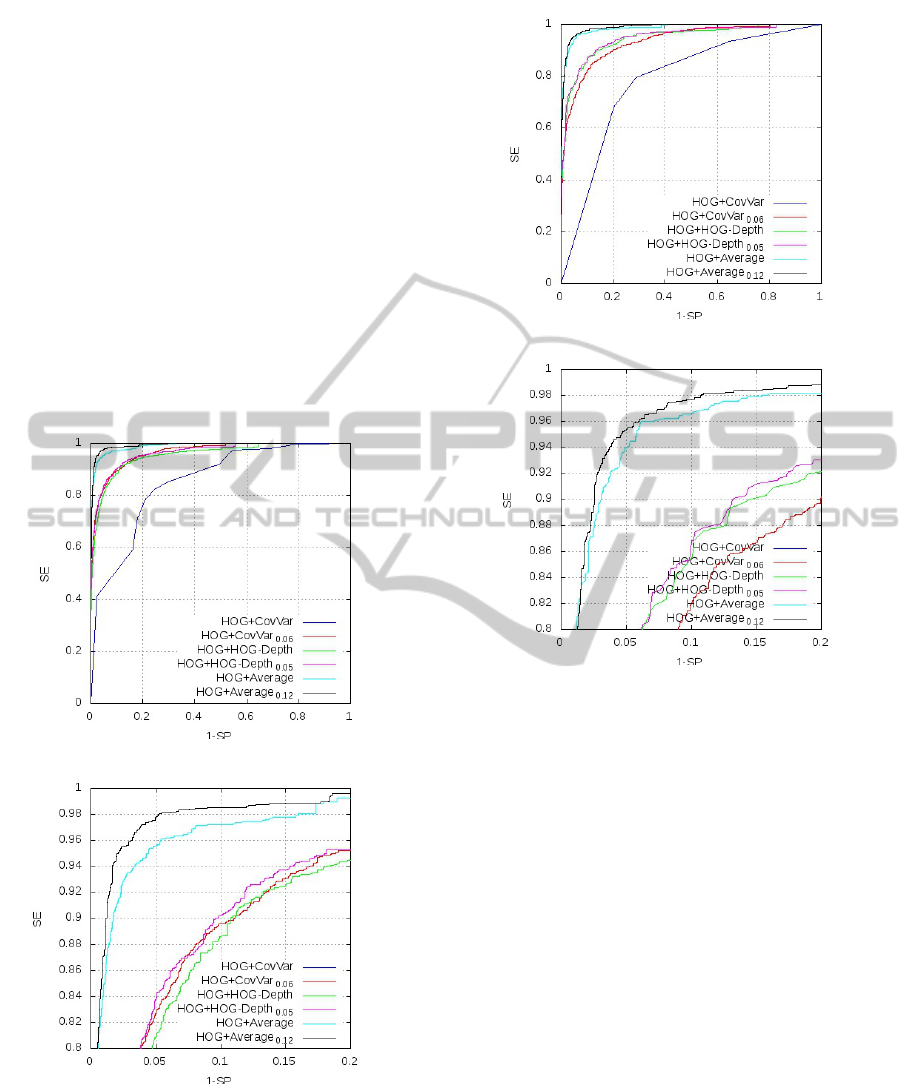
HOG+HOG-Depth. The protocol used is identical to

the one presented in section 2.2.1 (page 3). A maxi-

mum time limit lim for the time variable Λ

is deﬁned

to reﬂect the real-time constraint.

Best = arg

300

max

t=1



Sur f ace(Curve

) if Λ

6 lim

0 if Λ

> lim

(12)

The time limit lim is set to 2.5µs and 1.25µs cor-

responding respectively to 10 and 20 frames per sec-

ond. This time limit has been estimated to account

for a number of 40, 000 tests sub-window to evalu-

ate an image. Figure 10 (respectively 11) shows the

six ROC curves corresponding to lim = 2.5µs (respec-

tively lim = 1.25µs). Parts (a) represent the full curves

in the interval [0; 1] × [0;1], while parts (b) are zooms

in the interval [0; 0.2] × [0.8; 1].

(a) Interval [0;1] × [0; 1].

(b) Interval [0;0.2] × [0.8; 1].

Figure 10: ROC curves for comparison between a Ad-

aBoost and HAB for a computing time Λ

6 2.5µs.

In both ﬁgures, curves HOG+Average (light blue),

HOG+CovVar (dark blue) and HOG+HOG-Depth

(green) are learned with a classical Adaboost. The

(a) Interval [0;1] × [0; 1].

(b) Interval [0;0.2] × [0.8; 1].

Figure 11: ROC curves for comparison between a Ad-

aBoost and HAB for a computing time Λ

6 1.25µs.

others curves are learned with HAB and a coefﬁ-

cient α determined accordingly to the protocol pre-

sented above. The coefﬁcient α is equal 0.12 for

HOG+Average (black), 0.06 for HOG+CovVar (red)

and 0.05 for HOG+HOG-Depth (purple). In both ﬁg-

ures, the curves generated by HAB present a detec-

tion rate (SE) better than their counterparts produced

by classical Adaboost regardless of the false positive

rate (1-SP).

On the other hand, whatever the selected time, the

best strong classiﬁer is given by HOG+Average learn-

ing (black).

The ﬁgure 4 (of page 3), showed that the CovVar

method is more efﬁcient than HOG-Depth. However,

the CovVar algorithmic cost is ten times higher than

the HOG-Depth (ﬁgure 5). The ﬁgures 10 and 11

show that the merger by HAB leads to a combination

HOG+HOG-Depth that outperforms HOG+CovVar.

HETEROGENEOUS ADABOOST WITH REAL-TIME CONSTRAINTS - Application to the Detection of Pedestrians by

Stereovision

545

4 CONCLUSIONS AND

PROSPECTS

In this paper, in a ﬁrst part, we have proposed and pre-

sented different descriptors of the depth map. Follow-

ing of the tests results the Average descriptor provides

performance equivalent to HOG descriptor which is

our reference.

In a second part, we have proposed a change of

the Adaboost algorithm taking account of the algo-

rithmic cost λ

for the selection of each weak classi-

ﬁer. This new algorithm (HAB) has been evaluated on

the fusion of a appearance descriptor (HOG) with de-

scriptors of the depth map (CovVar, HOG-depth and

Average). The ROC curve which has a ﬁxed process-

ing time, is superior to the conventional Adaboost ap-

proach. The output of HAB algorithm evaluates Al-

gorithms cost of strong classiﬁer Λ

also.

The HAB algorithm could be adapted to the use

of a cascade (Viola and Jones, 2001) by setting a pro-

cessing time of each ﬂoor. In addition, the computa-

tional cost of each classiﬁer can be redeﬁned at each

stage in order to favour slow but efﬁcient detectors at

the end of the cascade.

REFERENCES

Begard, J., Allezard, N., and Sayd, P. (2008). Real-time hu-

man detection in urban scenes: Local descriptors and

classiﬁers selection with adaboost-like algorithms. In

Computer Vision and Pattern Recognition Workshops,

2008. CVPRW ’08. IEEE Computer Society Confer-

ence on, pages 1–8.

Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-

dients for human detection. In Computer Vision and

Pattern Recognition, 2005. CVPR 2005. IEEE Com-

puter Society Conference on, volume 1, pages 886–

893.

Dalal, N., Triggs, B., and Schmid, C. (2006). Human de-

tection using oriented histograms of ﬂow and appear-

ance. In In European Conference on Computer Vision.

Springer.

Enzweiler, M. and Gavrila, D. (2011). A multilevel

mixture-of-experts framework for pedestrian classiﬁ-

cation. Image Processing, 20(10):2967–2979.

Ess, A., Leibe, B., Schindler, K., , and van Gool, L. (2008).

A mobile vision system for robust multi-person track-

ing. In IEEE Conference on Computer Vision and Pat-

tern Recognition (CVPR’08). IEEE Press.

Freund, Y. and Schapire, R. E. (1999). A short introduction

to boosting. Journal of Japanese Society for Artiﬁcial

Intelligence, 14(5):771–780.

Friedman, J., Hastie, T., and Tibshirani, R. (1998). Addi-

tive logistic regression: a statistical view of boosting.

Statistics, Stanford University Technical Report.

Tuzel, O., Porikli, F., and Meer, P. (2008). Pedestrian

detection via classiﬁcation on riemannian manifolds.

Transactions on Pattern Analysis and Machine Intel-

ligence, 30:1713–1727.

Viola, P. and Jones, M. (2001). Rapid object detection using

a boosted cascade of simple features. Computer Vision

and Pattern Recognition.

Walk, S., Schindler, K., and Schiele, B. (2010). Disparity

statistics for pedestrian detection: Combining appear-

ance, motion and stereo. ECCV, pages 182–195.

Wojek, C., Walk, S., and Schiele, B. (2009). Multi-cue on-

board pedestrian detection. In Computer Vision and

Pattern Recognition, 2009. CVPR 2009. IEEE Con-

ference on, pages 794–801.

Yoa, J. and Odobez, J. (2008). Fast human detection from

videos using covariance features. In 8th European

Conference on Computer Vision Visual Surveillance

workshop, Marseille.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

546