ALGORITHM TO MAINTAIN LINEAR ELEMENT IN 3D LEVEL

SET TOPOLOGY OPTIMIZATION

Christopher J. Brampton, Alicia H. Kim and James L. Cunningham

Department of Mechanical Engineering, University of Bath, Bath, U.K.

Keywords: Level set method, 3D topology optimization, Voxel mesh.

Abstract: In level set topology optimization the boundary of the structure is defined by level set function values stored

at the nodes of a regular gird of simple bilinear elements. By changing the level set function values

according to optimization sensitivities the boundary of the structure is moved to create an optimal structure.

However it is possible for the boundary to cut an element more than once; violating the linear element

assumptions resulting in insufficient nodal information for the optimization sensitivity calculations. To

resolve this the local boundary of the structure is moved so that each element is only cut once. In 2D where

a square element mesh is used an element cut twice times is altered by moving one of the boundaries within

the element to intercept the node closest to it removing the extra cut from the element. In 3D where a voxel

mesh is used the process of moving the boundary within an element is more complicated due to the greater

number of boundary cuts possible and the effect that it can have on neighbouring elements. An algorithm is

developed which allows the boundary within a 3D element to be moved with these considerations taken into

account.

1 INTRODUCTION

Topology optimization is considered to have enabled

a step-change in structural design as it is the most

generalized form of structural optimization

producing a solution least dependent on the initial

design. It usually starts with a continuum of the

available design space and finds the optimal

topology as well as shape and size of the structural

members within it. One parameterization that is

receiving much interest in recent years is the level

set method due to its flexibility and stability in

handling topological changes (Allaire et al., 2004).

Topology optimization is an iterative process

where a finite element analysis is applied to carry

out the sensitivity analysis. The local sensitivities

are then used to update the level set function values,

thus modifying the structural boundaries to create an

improved structural geometry. To avoid the need for

a new finite element mesh every iteration the

geometry is usually projected onto a regular mesh of

elements (Allaire et al., 2004). Since the finite

element analysis is the computational bottleneck of

optimisation simple 1

order bilinear elements (4

node rectangular elements in 2D and 8 node brick

elements in 3D) are most commonly used in

topology optimisation (Dunning and Kim, 2011).

For convenience finite element nodes are used to

define the level set function. As the geometric

boundary defined by the level set function does not

always conform to the regular element edges, there

is a group of boundary elements which are cut by the

boundary. A variety of methods have been used to

estimate the material properties of these elements,

from simple element volume ratio based calculations

(Allaire et al., 2004) (Jang and Kim, 2005) (Wang et

al., 2007) to local remeshing approaches (Wang and

Wang, 2006).

A popular approach is to compute local

sensitivities per element for the level set function

update (Allaire et al., 2004) (Jang and Kim, 2005).

This means the elemental properties are

homogenised and the nodal properties are

approximately computed by interpolating the

elemental properties, instead of using the more

accurate nodal values from finite element analysis.

Nodal sensitivities can be used directly to update the

level set function (Dunning and Kim, 2011).

However this means an element can be cut by two

boundaries. In these cases, there are insufficient

nodes for the subsequent finite element analysis to

describe the linear displacement field of the element,

341

J. Brampton C., H. Kim A. and L. Cunningham J..

ALGORITHM TO MAINTAIN LINEAR ELEMENT IN 3D LEVEL SET TOPOLOGY OPTIMIZATION.

DOI: 10.5220/0003860003410350

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods (SADM-2012), pages 341-350

ISBN: 978-989-8425-98-0

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

thus sensitivities cannot be computed for the next

iteration.

Several methods have been devised to resolve

the problem of elements containing multiple

boundaries. The simplest is to declare cut elements

to be entirely outside the structure (Challis, 2010),

however this is a significant simplification and

increases the mesh density required for accurate

optimization. Researchers have employed the

extended finite element method (X-FEM). This has

been developed primarily for describing fractures

and multi-scale analysis where the elemental

stiffness matrix is “enriched” to describe the local

material distribution. However, higher order

elements must be used at the geometric boundary to

accomplish this (Belytschko et al., 2003) (Wei et al.,

2010). The local mesh refinement method splits each

cut element into multiple elements which are fitted

to the geometric boundary (Wang and Wang, 2006).

However both these methods require an increase of

the degrees of freedom with considerable additional

computation. This increases the computational cost

of the finite element analysis which is already a

processing bottle neck.

This paper proposes an alternative method to

resolve the problem of elements containing multiple

cuts without increasing the degrees of freedom in the

finite element model. The proposed approach is to

alter the local boundary geometry so that no

elements contain multiple boundaries allowing first

order bilinear elements to be used on the geometric

boundary. This allows the use of accurate nodal

properties to compute the sensitivities and avoids the

unnecessary additional computational complexity.

The numerical results show that the boundary “fix”

proposed in this paper is sufficiently minimal and

the algorithm consistently finds the optimum

solutions.

2 BOUNDARY MODIFICATION

IN 2D

2.1 Problem Statement

The level set topology optimization procedure

moves the structural boundary by cutting through

elements. As a result it is possible for multiple

boundaries to simultaneous cut through an element.

When 1

order elements are used, there is

insufficient nodal information for sensitivity

computation in elements containing multiple

boundary cuts and thus, they are considered

“illegal”. In order to proceed with the topology

optimization procedure any illegal elements must be

avoided.

In 2D this occurs when an element is cut twice,

usually due to a narrow strut or a small hole in the

structure. An example of a legal and illegal element

can be seen in Figures 1 and 2, respectively.

Figure 1: Legal 2D Element. The structure is indicated by

the shaded region.

Figure 2: Illegal 2D Element.

2.2 Treatment for Illegal Elements

A simple and computationally efficient method is to

move the boundary such that all elements contain a

maximum of one cut. To identify the illegal

elements we examine the status of the element

nodes.

The implicit level set function representation

usually has two node statuses, a node is inside the

structure (an I-node) if the level set function is

positive and is outside the structure (an O-node) if

the level set function is negative. An element is cut

by the boundary if it is made of both I-nodes and O-

nodes. Similarly an edge of the element is cut if it

has an I-node on one end and an O-node on the

other. In 2D an element is considered illegal if an

element contains two I-nodes and O-nodes in

opposite corners as seen in Figure 2. In this case the

element contains more than two cut edges, this

identifies an illegal element in 2D.

We introduce a new node status, a touching node

(a T-node) that is considered to be exactly on the

boundary of the structure. A T-node can be either

inside or outside depending on the status of the

nodes it shares an edge with. If a T-node shares an

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

342

edge with an I-node the edge is inside the structure,

if it shares an edge with an O-node the edge is

outside the structure. Hence, a T-node is inside the

structure if both edges it is connected to are inside

and outside if both edges it is joined to are outside.

If one edge is outside the structure and the other

inside the structure the boundary intercepts the T-

node.

Figure 3: Examples of boundary updates to avoid illegal

elements using T-nodes. The illegal elements on the left

and modified legal elements on the right.

By changing an I-node or O-node in an illegal

element to a T-node the boundary immediately

adjacent to the T-node is moved as shown in Figure

3. This moves the boundary outside the element so

that it no longer cuts the neighbouring edges and

only one boundary remains, making the element

legal. To minimize the modification, the node that is

the shortest distance away from the boundary, as

defined by its level set function value, is selected to

be changed to a T-node.

This boundary modification algorithm is applied

every iteration after an optimization step and Figure

4 shows an example of the effect it can have on the

topological solution. In order to minimize the effects

of this algorithm on the overall optimization

procedure, it is assumed that the mesh density is of a

reasonable density.

3 BOUNDARY MODIFICATION

IN 3D

The additional dimension in 3D level set topology

optimization significantly increases the complexity

of the necessary algorithm both to identify and

eliminate the illegal elements. To achieve robust

treatment of illegal 3D elements a more advanced

Figure 4: An example of how treating an illegal element

affects the global structure. Nodes A and B are changed to

T-nodes. The mesh density should be high enough for

these features to be considered to be minimal.

correction method is formulated as discussed in the

following.

3.1 Identification of Illegal 3D

Elements

A 3D element is considered illegal if a boundary of

the structure cuts the element in a manner that

cannot be represented by a single linear cut. Again

this occurs when the boundary of the structure cuts

an element more than once. Figure 5 shows

examples of legally cut 3D elements and Figure 6

features examples of illegal elements showing that in

3D between two and four separate cuts by the

boundary are possible. This complicates the

detection of illegal elements as there is not a clear

relationship between the number of cut edges and

the illegal elements. While the maximum number of

cut edges in a legal element is 6 (Figure 5), the same

number of cuts can produce an illegal element

(Figure 6). Introducing T-nodes does not lead to a

well-defined relationship between the number of cut

edges and illegal elements, as shown in Figure 7.

ALGORITHM TO MAINTAIN LINEAR ELEMENT IN 3D LEVEL SET TOPOLOGY OPTIMIZATION

343

Figure 5: Examples of legally cut 3D elements.

Figure 6: Example of illegal 3D elements that have been

cut more than once. It is possible for an element to be cut

four times.

Figure 7: Example of 3D elements containing T-nodes.

Element A is legal. Elements B and C illegal are as the T-

nodes are intercepted by the boundary within the element

in a manner that cuts the volume of material in two.

Another approach that could be used to identify

an illegal element would be to check that all the I-

nodes and O-nodes are linked by edges that are not

cut. This would suggest a single section of the

element containing all the I- and O-nodes and hence

a single linear cut. However, it is unclear how to

classify T-nodes; examples of this are shown in

Figure 7. In addition, Figure 8 shows an illegal

element with four I-nodes and O-nodes linked by

uncut edges. We nickname this case the “Impossible

4” because it is impossible to form a legal cut that

satisfies these node statuses, to do this two

overlapping cuts are required.

We therefore, propose a binary index method.

This method has been used to identify the type of

boundary cut through an element for surface

reconstruction (Bourke, 1994) and we develop this

concept to identify illegal elements. The method

assigns each node in the element a binary value

based on its status. All O-nodes are assigned 0. Node

0 in Figure 9 is assigned 1 if it is an I-node and 256

if it is a T-node, node 1 is given 2 if it is an I-node

and 512 if it is a T-node and so on with the values

doubling for each node as a binary number. The full

list of the values related to the node status is shown

Figure 8: Example of the “Impossible 4”. All the I-nodes

are connected to each other by uncut edges but two

boundaries meet inside the element, making it illegal.

in Table 1 and the local position of each node is

shown in Figure 9.

Figure 9: Local mode numbering of an element.

Table 1: Value assigned to each of the local nodes based

off the node status.

Node I-node T-node O-node

0 1 256 0

1 2 512 0

2 4 1024 0

3 8 2048 0

4 16 4096 0

5 32 8192 0

6 64 16384 0

7 128 32768 0

Summing up the value of each node produces a

number that is unique for each possible element cut.

The sum of the index value for each element

therefore, is used to identify the legal elements.

There are 2554 legal cuts whose values are all

stored in the index. Examples of this method of

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

344

Figure 10: Example of the binary point method. Element

A is legal; 25 is in the legal element index. Element B is

illegal; 89 is not in the legal element index.

identification are shown in Figure 10 applied to a

legal element (A) and an illegal element (B).

As well as having the advantage of being simple

the method is also computationally inexpensive.

This is an important characteristic as the binary

index method is used to check element legality at

every iteration of optimization.

3.2 Further Issues in 3D Elements

After an optimization step to update the structural

boundaries and the illegal elements are identified

using the binary index method the boundaries must

be modified to eliminate the illegal elements. This

step moves the boundaries in illegal elements such

that there is only one surface cut through the

element. This is implemented by changing the status

of nodes to T-nodes, which follow the same rules in

3D as in 2D. However there are several cases that

are unique to 3D geometry.

Firstly in 2D all the illegal elements could be

fixed by changing one node to a T-node. However

this is not the case in 3D. Figure 11 shows a case

where two nodes need to be changed to T-nodes to

remove one of the cuts. Investigation has shown that

the maximum number of node changes required to

correct any illegal element cut is two, including an

element cut four times and the Impossible 4 as

shown in Figure 12.

Figure 11: Cases where changing one node to a T-node

does not make the element legal. Two neighbouring nodes

must be changed.

The second issue is that unlike 2D modelling,

changing the node closest to the boundary to a T-

node does not guarantee the smallest shift in the

boundary. In Figure 13 the change that will produce

a legal element with the smallest movement of the

boundary is to change node A to a T-node and

remove the pyramid of material around it. However

changing the node closest to the boundary would

change node B which would not make the element

legal. A more robust method of node selection is

required in 3D.

Finally changing a node to a T-node can result in

an illegal neighbouring element that shares the node.

In Figure 14 changing node X to a T-node makes

element A legal but it causes the neighbouring

element B to become illegal. To prevent this it is

necessary to check that changing a node to a T-node

does not make neighbouring elements illegal.

Figure 12: Illustration of how only one or two T-nodes are

required to eliminate an illegal cut even when the element

is cut four times as in case A. One node is required to be

changed to a T-node make an Impossible 4 legal in case B.

ALGORITHM TO MAINTAIN LINEAR ELEMENT IN 3D LEVEL SET TOPOLOGY OPTIMIZATION

345

Figure 13: In this case changing the node closest the

boundary (node B) to a T-node does not make the element

legal. The least significant change to make the element

legal is to change node A to a T-node.

3.3 Fractured Elements

Due to the need to maintain legality in neighbouring

elements during the boundary modification

procedure in 3D it is possible that a simple change

of nodes of an illegal element to T-nodes is not

sufficient in eliminating all illegal elements. This

problem occurs in regions where there are multiple

structural boundaries close together. As a result

moving a boundary cut out of one element results in

an extra boundary cut appearing in neighbouring

elements. This suggests that the local structure is

porous, formed from struts that are narrower than an

element and/or islands of disconnected material.

Finite element analysis results in porous local

structures described by just a few disconnected

elements have poor accuracy and such structures are

usually a product of numerical instability such as

chequerboard patterns well-known in topology

optimization. We therefore, consider elements in

such local porous regions to be “fractured” where all

nodes in the elements are changed to T-nodes. With

no I-nodes left a fractured element is considered to

be outside the structure and hence makes no

contribution to its stiffness.

It is worth noting that fractured elements are not

a common occurrence in topology optimization;

none occur during either of the example models

shown in Figure 16 or Figure 18. If a model

produces many fractured elements, it means the

mesh is too coarse to further optimize the structure

and the mesh should be refined.

3.4 Boundary Update Algorithm for 3D

Level Set Topology Optimization

Having considered all cases for identifying and

eliminating illegal elements in 3D the following

algorithm is formulated for level set topology

optimization. This algorithm follows the usual level

set topology optimization boundary update to

eliminate illegal elements. A flow chart of this

method can be seen in Figure 15.

The first step is to identify the elements that the

Figure 14: An example when making element A legal by

changing node X into a T-node consequently makes

element B illegal.

boundary passes through by examining the node

statuses of each element. If an element contains at

least one I-node and one O-node then it is cut by a

boundary; if it has no I-nodes it is entirely outside

the structure; otherwise it is entirely inside the

structure. If an element is cut by a boundary its

legality is checked using the binary indexing method

described in Section 3.1, if the element is illegal then

it is added to the correction set. Only once the

legality of all the elements has been established does

the correction procedure begin.

For each of the elements in the correction set, the

algorithm searches for the correction that would

make the elements legal and minimize the necessary

boundary modification. The algorithm begins by

changing the status of one node only. Each node in

turn is temporarily changed to a T-node and the

binary index method is used to check if the change

has made the element legal. If so the legality of the

neighbouring elements that share the node and are

currently legal is checked to make sure the change

has not made any of these elements illegal. If all the

legal neighbouring elements remain legal then this

modification is considered a potential solution. If

there is more than one possible solution, the

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

346

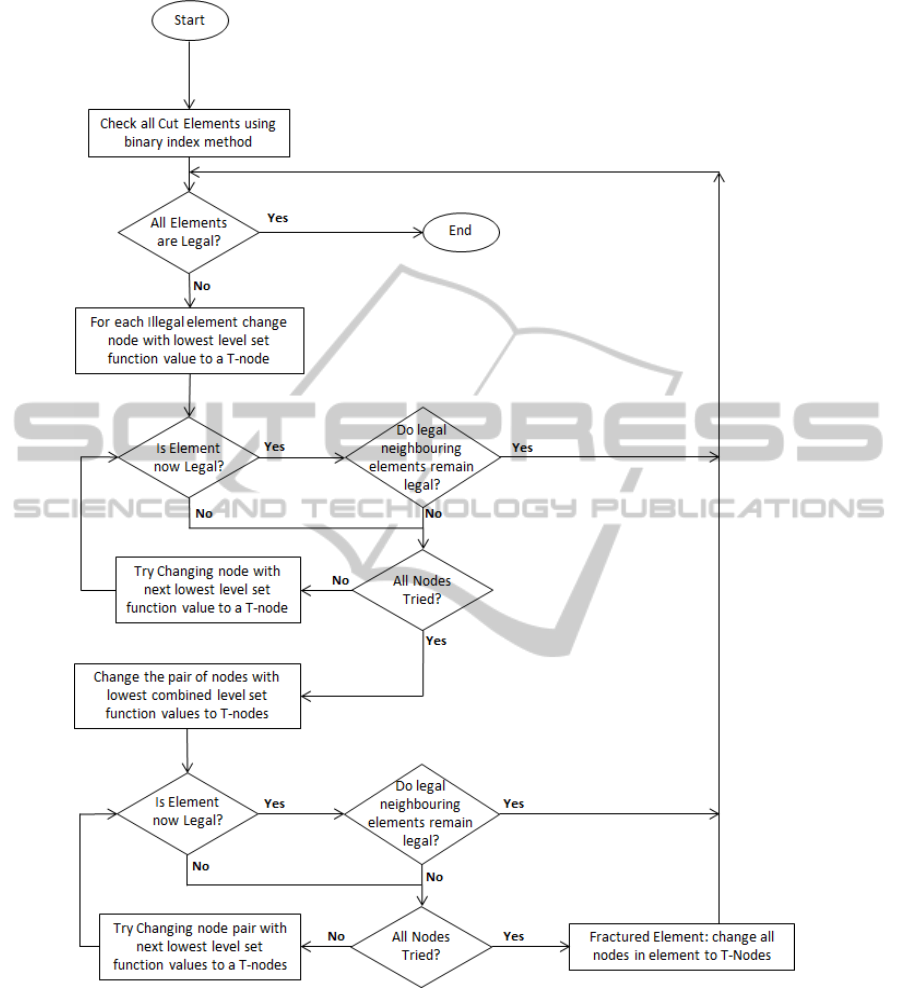
Figure 15: Flow chart for boundary correction algorithm.

one with the smallest level set function value (thus

closest to the boundary) is selected and turned into a

T-node to make the minimal change to the optimum

boundary.

If there are no possible solutions from simply

changing a single node to a T-node, a pair of nodes

is temporarily changed to T-nodes to find a two-

node solution. Again, of all the possible two-node

solutions, the lowest combined level set function

value is selected to be turned into T-nodes to make

the element legal.

In the rare situation that no suitable correction is

found changing either one or two nodes to T-nodes

then the element is considered to be fractured as

described in Section 3.3. All its nodes are turned into

T-nodes removing it from the structure. All the

neighbouring elements are then examined, to

investigate if this modification made the

ALGORITHM TO MAINTAIN LINEAR ELEMENT IN 3D LEVEL SET TOPOLOGY OPTIMIZATION

347

neighbouring elements illegal. All the new illegal

elements are then added to the correction set.

Once all illegal elements are considered and the

correction set is empty, the new solution is checked

for convergence and the optimization procedure

continues.

An example of the effect this algorithm can have

on the topological solution is shown in Figure 16. As

in 2D modelling a reasonable mesh density is

required to minimize the effect of this process on the

optimal boundary.

4 NUMERICAL RESULTS

The boundary update algorithm described in Section

3 ensures that there is always sufficient nodal

information to perform sensitivity computation

allowing the optimization process to reliably

proceed. This section illustrates the numerical

examples of the topology optimization.

Figure 17 shows level set topology optimization

of a 2D cantilever beam with aspect ratio 2. The

structure displays features that would be expected in

the optimum solution which is well-known (Michell,

1904). The thick beam is positioned at the top and

bottom of the design space to resist the bending of

the structure. In the centre where less bending is

strain is experienced smaller diagonal struts are

formed to provide support for the exterior structure.

A similar cantilever beam of aspect ratio 2 is

created in 3D on a course 61x30x10 mesh with a

central load downwards, as shown in Figure 18.

Figure 18 B to D shows how the structure develops

during the optimization procedure. Starting from

fully-populated continuum (B) the boundary moves

towards the optimum topology by removing material

in the centre of the beam first; leaving more material

at the top and bottom of the structure to maintain a

higher second moment of area and reduce bending.

The converged topology adopts similar features to

the 2D solution with thick beams around the outside

of the structure supported in the centre by a thinner

“web” made of multiple struts, similar to an I-beam.

5 CONCLUSIONS

During level set topology optimization it is possible

for the boundary of the structure to move in a

manner that cuts an element more than once. This

violates the modelling assumptions for 1

order

bilinear elements which cannot accurately represent

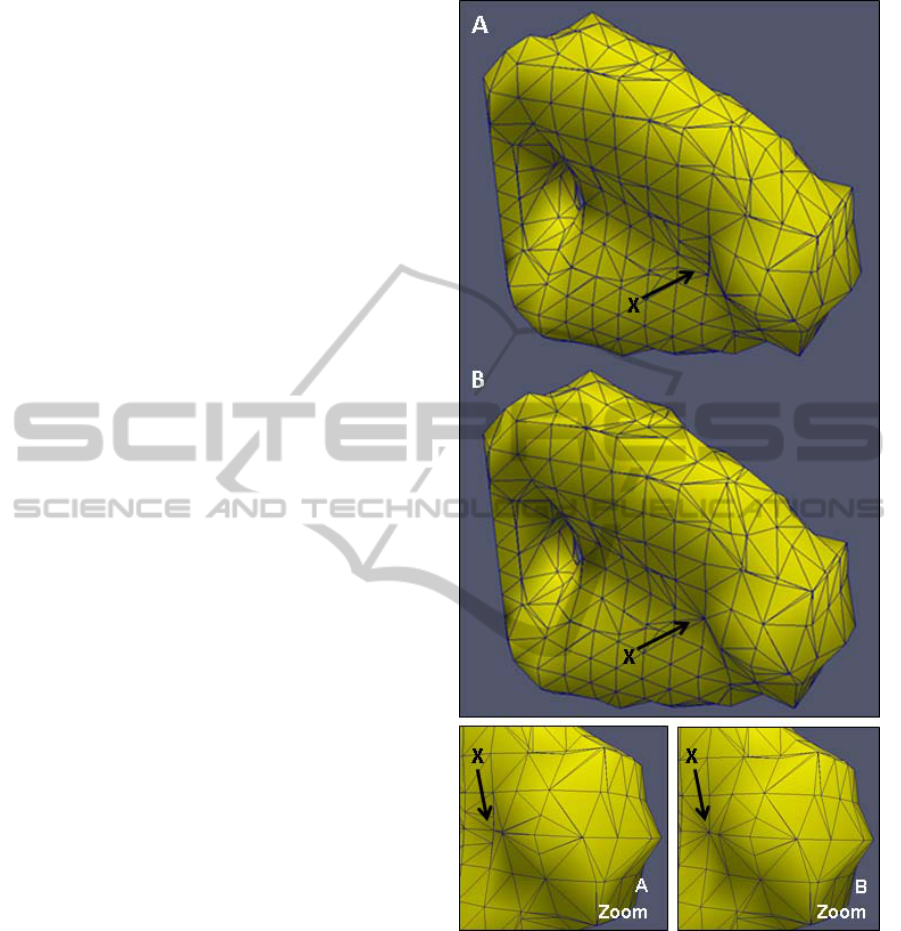
Figure 16: Example of how the treatment of illegal

elements affects the global structure. A shows the

structure before the element correction process. Arrow X

points to a sharp indent in the structure which cuts two

elements illegally. The correction procedure changes 4

nodes attached to these elements to T-nodes to make both

elements legal. The movement of the boundary flattens the

indent as can be seen in B; however this shift is small and

does not have a significant effect on the global topological

solution. (Note: the triangular surface mesh in these

images represents the mesh for visualization and is not

used for analysis or optimization. It is shown to highlight

the structural details.)

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

348

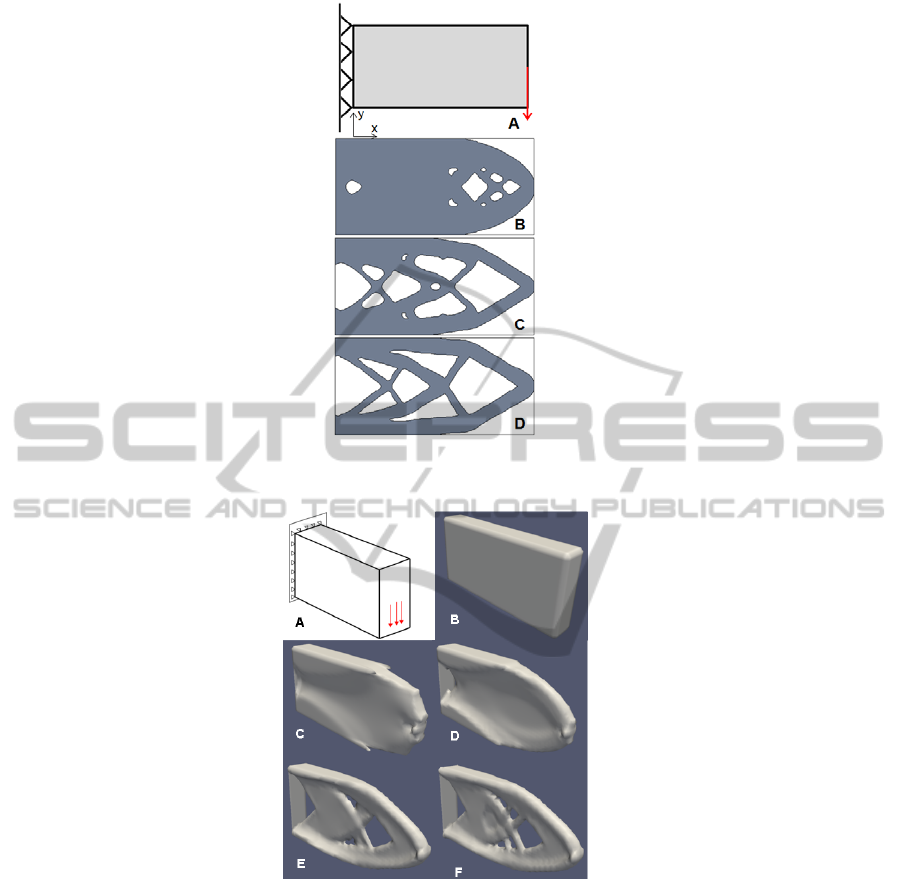
Figure 17: An Example of level set topology optimization applied to a simple cantilever beam in 2D. The modelled

situation is show in A with the development of the optimal structure is shown in images B to D.

Figure 18: Example of 3D level set topology optimization applied to a simple cantilever beam on a 61x30x10 mesh. A

shows the modelling situation and B to F show stages of the structure development from the initial continuum structure to

the final optimal structure.

two boundaries in one element. Such element cuts

are considered illegal. This paper presented a

method to make illegal element cuts legal during

level set topology optimization.

A binary index method is used to efficiently and

reliably detect illegal elements. The algorithm then

identifies the extra boundary, or boundaries, closest

to the edge of the elements and moves it outside the

element to make the element legal. The possibility of

this movement making a neighbouring element

illegal is considered by the algorithm and prevented.

Even with a relatively coarse mesh density this

method does not have a significant effect on the

global solution and produces the optimum topology.

The implementation of this method allows the

use of a regular grid of first order bilinear elements

on the geometric boundary of nodal sensitivity based

level set topology optimization. The successful

optimum solutions in 2D and 3D numerical

examples demonstrate the methods reliability and

suitability for level set topology optimization.

Possible extensions include the interface between

two materials in composite structures and contact

modelling between two surfaces. This will be

ALGORITHM TO MAINTAIN LINEAR ELEMENT IN 3D LEVEL SET TOPOLOGY OPTIMIZATION

349

investigated in future works.

REFERENCES

Allaire G., Jouve F., Toader AM., 2004. Structural

optimization using sensitivity analysis and a level-set

method. Journal of Computational Physics; 194(1):

363-393.

Dunning P D., Kim H A., 2011. Investigation and

improvement of sensitivity computation using the

area-fraction weighted fixed grid FEM and structural

optimization. Finite Elements in Analysis and Design;

47: 933-941.

Jang G., Kim Y Y., 2005. Sensitivity analysis for fixed-

grid shape optimization by using oblique boundary

curve approximation. International Journal of Solids

and Structures; 42: 3591-3609.

Wang S Y., Lim K Y., Khoo B C., Wang M Y., 2007, An

extended level set method for shape and topology

optimization. Journal of Computational Physics; 221:

395-421.

Wang S., Wang M Y., 2006, A moving superimposed

finite element method for structural topology

optimization. International Journal for Numerical

Methods in Engineering; 65:1892-1922.

Challis V J., 2010, A discrete level-set topology

optimization code written in Matlab. Structural and

Multidisciplinary Optimization; 41(3): 453-464.

Belytschko T., Parimi C., Moës N., Sukumar N., Usui S.,

2003, Structured extended finite element methods for

solids defined by implicit surfaces. International

Journal for Numerical Methods in Engineering; 56;

609-635.

Wei P., Wang M Y., Xing X., 2010, A study on X-FEM in

continuum structural optimization using a level set

model. Computer-Aided Design; 42: 708-719.

Bourke P., 1994. Polygonising a Scalar Field. http://

paulbourke.net

Michell A. G. M., 1904. The limits of economy of

material in frame-structures; Royal Society

Philosophical Magazine; 8: 589–597

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

350