UNITY IN DIVERSITY: DISCOVERING TOPICS FROM WORDS
Information Theoretic Co-clustering for Visual Categorization
Ashish Gupta and Richard Bowden
Centre for Vision, Speech and Signal Processing, University of Surrey, Guildford, United Kingdom
Keywords:
Co-clustering, Bag-of-Words, Visual Topic Model.
Abstract:
This paper presents a novel approach to learning a codebook for visual categorization, that resolves the key is-
sue of intra-category appearance variation found in complex real world datasets. The codebook of visual-topics
(semantically equivalent descriptors) is made by grouping visual-words (syntactically equivalent descriptors)
that are scattered in feature space. We analyze the joint distribution of images and visual-words using infor-
mation theoretic co-clustering to discover visual-topics. Our approach is compared with the standard ‘Bag-
of-Words’ approach. The statistically significant performance improvement in all the datasets utilized (Pascal
VOC 2006; VOC 2007; VOC 2010; Scene-15) establishes the efficacy of our approach.
1 INTRODUCTION
Visual categorization is a topic of intense research
activity in the computer vision and pattern recogni-
tion communities. Despite the progress made in the
past decade, a satisfactory model for a visual cate-
gory is missing. The difficulty lies in the fact that a
visual category is not a single entity is a composition
of distinct parts. These parts could be considered as
categories themselves. This contributes to significant
variation in appearance of a category. The high intra-
category appearance variation implies low-level fea-
tures associated with a semantically relevant part of
the category are scattered over feature space. A hard-
partitioning algorithm like Learning Vector Quantiza-
tion (LVQ) is unable to cluster these scattered features
together. This is the key issue that limits the abil-
ity of the standard ‘Bag-of-Words’ (BoW) approach
(Csurka et al., 2004), which uses LVQ, to build a
codebook of ‘visual-words’ that can effectively model
complex visual category data. Consequently, this pa-
per focuses on a novel approach that can cluster these
scattered features together, thereby providing a suc-
cinct and robust codebook of ‘visual-topics’ that can
better model complex category data.
The basic concept behind our approach can be vi-
sualized in figure 1. BoW partitions feature space
into disjoint regions and builds a codebook of ‘visual-
words’ using centroids of these regions. Two descrip-
tors from the same part of a category but located far
apart in feature space will be assigned to different
‘words’. The method we propose groups the ‘words’
Figure 1: Topic discovery from Words: semantically
equivalent but visually distinct words are grouped together.
The words of the same color in the bottom cube depict
words that have been grouped together, the color represents
a topic. Images are public domain samples generated by 3D
tessellation software Voro++, for details see (Rycroft et al.,
2006).
into which these descriptors fall and assigns them to
a ‘visual-topic’, thereby creating a codebook of ‘top-
ics’. This is depicted by regions in different parts of
space being of the same color, where color denotes
topic. This approach can also be considered as non-
contiguous clustering. The key insight is that clus-
628
Gupta A. and Bowden R..
UNITY IN DIVERSITY: DISCOVERING TOPICS FROM WORDS - Information Theoretic Co-clustering for Visual Categorization.
DOI: 10.5220/0003861206280633
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 628-633
ISBN: 978-989-8565-03-7
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

tering of descriptors should be jointly based on two
criteria: distribution density in feature space; distri-
bution across images. We utilize co-clustering which
optimally clusters on the joint distribution of these cri-
teria to discover topics from words.Some of the earli-
est work on co-clustering can be found in (Hartigan,
1972). It was further developed in the field of bio-
informatics for gene sequence clustering described in
(Cheng and Church, 2000). It was introduced as a
tool for data mining in (Dhillon et al., 2003) and in
(Dhillon, 2001). It was utilized in a computer vision
application in (Liu and Shah, 2007).
Our main contributions to this work are:
• We propose a novel approach to discovering vi-
sual topics from visual words using information
theoretic co-clustering.
• We thoroughly evaluate our approach against the
standard BoW approach and show consistent and
statistically significant improvement in classifica-
tion performance.
• We analyze the relevance of codebook size to dis-
cover an optimal size for the datasets considered.
• We explored the relation between our approach
and different types of visual categories to discover
special applicability to a specific type of category.
Figure 2: Visual Categorization System: data acquisition,
feature extraction, clustering, learning a word codebook,
co-clustering, learning a topic codebook, and classification.
Blue box has modules of the BoW approach, red box has
modules of our approach using co-clustering.
2 APPROACH
We first state the motivation for our novel approach
and then describe the system and the algorithm. We
have formulated our approach based on these insights:
• BoW is based entirely on feature space descrip-
tor density distribution to build a codebook and
ignores the distribution density of a codebook el-
ement across images.
• Unlike a visual word (particular instance of an cat-
egory part) a visual topic will almost always occur
in a positive sample of the category.
• Feature vectors sourced from a category part are
not completely scattered but exist in cliques in
feature space.
• Visual words from the same category have similar
occurrence distribution statistics across images.
Combining these insights, an algorithm that si-
multaneously considers: distribution in feature space;
distribution across images, when clustering feature
vectors should provide a codebook of topics we in-
tend to build. We arrange these two distributions as
a image-word data matrix, where the rows are im-
ages and columns are words. Co-clustering optimally
and simultaneously clusters the rows and column of
the data matrix. Therefore we employ it to discover
topics. The modules of a typical visual categoriza-
tion system is shown in figure 2. The modules in the
blue box are used in the traditional approach while
the red box contains modules implementing our ap-
proach. The remaining modules are common to both
approaches. This allows us an effective comparison
for both approaches. The stpng in our algorithm are:
1. Over-partition feature space: build a huge set of
words using an unsupervised clustering technique
based purely on descriptor density distribution in
feature space.
2. Compute the occurrence histogram of codebook
elements. In other words, compute their order-
less distribution in the image, for all images in the
dataset.
3. Analyze the joint distribution of images and
words. We utilize information theoretic co-
clustering to optimally cluster both images and
words. This translates to creation of blocks in the
image-word data matrix. The blocks tell us which
words are clustered together.
4. Combine the clustered words into topics and cre-
ate the topic codebook.
3 LEARNING CODEBOOK
In this section we discuss how a codebook is learned
by the BoW approach and by our approach.
3.1 Codebook-of-Words
The mathematical formulation of the BoW model: It
encodes visual data in high-dimensional space Ξ ⊆
R
d
by a set of code-words Q = {ψ
1
, ψ
2
, . . . , ψ
N
}.
These code-words are also called visual-words or
simply words, φ
i
[i]
N
1
∈ Ξ. The visual data is a set
of feature descriptor vectors {υ
1
, υ
2
, . . . , υ
M
}, where
UNITY IN DIVERSITY: DISCOVERING TOPICS FROM WORDS - Information Theoretic Co-clustering for Visual
Categorization
629

υ
j
[ j]
M
1
∈ Ξ. Each visual-word ψ
i
has an associated
section of the high dimensional space ξ
i
. So, the
visual data space Ξ is represented by {ψ
i
, ξ
i
} [i]
N
1
,
ψ ∈ R
d
, and ∪
N
i
ξ
i
= Ξ. There are several algorithms
for computing {ψ
i
, ξ
i
} [i]
N
1
, which is the codebook.
We use a LVQ algorithm which is called as k-means
clustering method. The algorithm poses the task as
an optimization problem, where the codebook Q is
optimized given data ϒ = {υ
1
, υ
2
, . . . , υ
M
} and a dis-
tortion measure D
φ
(·, ·). The distortion measure in an
information-theoretic setting using Kullback-Leibler
divergence is given as:
D
KL
(ψ, υ) =
D
p(υ), log
p(υ)
p(ψ)
E
(1)
The optimal solution for Kullback-Leibler metric is
given as:
{Q , Ξ}
∗
= arg min
Q
L
KL
(Q , D
KL
| ϒ) (2)
Consider a data-set Λ containing n images λ
i
[i]
n
1
.
An image λ
i
is described by a set of m feature vectors
υ
j
[ j]
m
1
(number of features m will vary in images).
The image λ
i
is encoded by an occurrence histogram
of the codebook elements. Each feature vector υ
j
in
λ
i
is associated with a visual word ψ
k
. The histogram
h
λ
i
of image λ
i
is an array {h
λ
i
,ψ
k
}[k]
N
1
, where h
λ
i
,ψ
k
is given by:
h
λ
i
,ψ
k
=
∑
m
j=1
1
ψ
k
,υ
j
1
ψ
k
,υ
j
=

1 if υ
j
∈ ξ
k
0 otherwise
(3)
3.2 Codebook-of-Topics
Co-clustering attempts to discover topics by analyz-
ing the joint distribution of images and visual words.
Visual topic is a selection of visual words that have
high occurrence frequency across images. The set of
visual words is given by {Q , Ξ} = {ψ
i
, ξ
i
}[i]
N
1
and the
set of visual topics is given by {T , Ξ} = {τ
j
, ζ
j
}[ j]
M
1
.
Each topic is a cluster of visual words acquired by co-
clustering. So, a visual topic τ
j
= {ψ
1
, ψ
2
, . . . , ψ
t
j
and
its associated section of feature space is ζ
j
= ∪
t
j
t=1
ξ
t
.
In the co-clustering scheme all visual words are as-
signed to some visual topic, and so the union of topic
space is the entire feature space, ∪
M
j=1
ζ
j
= Ξ. To vi-
sualize this see figure 1.
4 CO-CLUSTERING
A mathematical formulation of co-clustering: Let W
and Y be discrete random variables that take values
in sets w
u
, [u]
m
1
and y
v
, [v]
n
1
. Here W represents vi-
sual word and Y represents image. In the ideal case,
the joint distribution p(W, Y) is known. This is the
normalized joint distribution of visual words and im-
ages. The aim is to cluster W into k disjoint clusters
w
g
, [g]
k
1
, and Y into l disjoint clusters ˆy
h
, [h]
l
1
. Let
ˆ
W and
ˆ
Y denote the corresponding clustered random
variables. The information-theoretic approach to op-
timal co-clustering is to solve:
min
ˆ
W ,
ˆ
Y
I(W, Y ) − I(
ˆ
W ,
ˆ
Y )
where I(W, Y ) is the mutual information between W
and Y . As shown in (Dhillon et al., 2003), information
loss is:
I(W, Y ) − I(
ˆ
W ,
ˆ
Y ) = D(p(W, Y ) k q(W, Y )) (4)
where D(· k ·) denotes KL-divergence, and q(W, Y ) is
given by:
q(W, Y ) = p(
ˆ
W ,
ˆ
Y )p(W |
ˆ
W )p(Y |
ˆ
Y ) (5)
It combines both row and column clustering at each
step. Row clustering is done by computing proximity
of each row distribution, in relative entropy, to cer-
tain ‘row cluster prototypes’. These are the estimated
cluster centroids. Column clustering is carried out in
a similar way. This two-part process is iterated till
mutual information converges to a local minimum.
5 EXPERIMENTS AND RESULTS
To quantitatively evaluate our novel approach we test
it using several of the popular datasets in the commu-
nity selected on basis of: popularity for benchmark
testing; number of categories within the dataset; na-
ture of the constituent visual categories. The visual
feature descriptor utilized is SIFT (Lowe, 2004). We
use k-means clustering for the purpose of partition-
ing feature space. A k-nearest neighbor (kNN) classi-
fier is used to evaluate the performance gain achieved
by our approach over the standard BoW approach. A
popular alternative classifier is the SVM. Our choice
if motivated by the work in (Boiman et al., 2008),
which defends k-NN vs. classifier like SVM; and
use of k-NN in (Horster et al., 2008). In order to un-
derstand the performance of our approach with code-
book size, we experiment with different topic code-
book sizes.
5.1 Setup
In this paper we are learning category specific code-
books. Negative training samples are collated from
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
630

Table 1: Expt. Scene-15: Comparison of information theoretic co-clustering in terms of performance gain over the BoW
model. The dataset utilized is Scene-15. The graphs show the F
1
-score for each technique across the visual categories in the
dataset. The codebook sizes are 100, 500, and 1000.
Table 2: Expt. Pascal VOC-2006: Comparison of information theoretic co-clustering in terms of performance gain over the
BoW model. The dataset utilized is Pacal VOC-2006. The graphs show the F
1
-score for each technique across the visual
categories in the dataset. The codebook sizes are 100, 500, and 1000.
other categories in the dataset. The feature detec-
tor and descriptor SIFT detects on average a thou-
sand interest points per image. PCA (Ke and Suk-
thankar, 2004) is used to project the feature space
to 13 dimensions, based on a study of intrinsic di-
mensionality of visual descriptor data in (Gupta and
Bowden, 2011). K-means clustering is utilized with
Euclidean distance metric; randomly generated ini-
tial cluster centroids; and upper limit of 100 itera-
tions. The k-NN classifier had a neighborhood size
of 10. Classification performance was measured us-
ing F
1
score, which is the harmonic mean of precision
and recall. It is commonly used for measuring docu-
ment retrieval and classification performance.
F
1
= 2 ·
precision ·recall
precision +recall
(6)
We over-partition space to compute a huge codebook
of 10000 words. We compute a word codebook of the
same size as the topic codebook to be learned. We
use 10 fold cross-validation in estimating the classi-
fication performance for both approaches. In all the
graphs showing results of the experiments, the solid
line is the F
1
score for our approach and the dashed
line represents the BoW approach.
5.2 Expt. Scene-15
In this experiment we evaluate our approach against
BoW for Scene-15 dataset. It has 15 visual categories
of natural indoor and outdoor scenes. Each category
has about 200 to 400 images and the entire dataset has
4485 images. Details can be found in (Fei-fei, 2005).
We present results for different sizes of the topic code-
book: { 100, 500, 1000 }. The results are shown in
table 1. The graphs show the F
1
score for different
categories in Scene-15. The difference in F
1
scores
between our approach and BoW is consistently large
and remarkably better than it is for VOC-2006 and
VOC-2007. This is an interesting result and alludes to
the possibility that the nature of scene descriptor data
is comparatively more amenable to our approach.
5.3 Expt: Pascal VOC-2006
In this experiment we evaluate our approach against
BoW for Pascal VOC-2006 dataset. It is an early edi-
tion of the series of datasets used in the annual object
categorization challenge. Several papers in literature
report results using this dataset. It has 10 visual cat-
egories with about 175 to 650 images per category.
There are a total of 5304 images. Images do contain
instances of multiple categories. Details can be found
UNITY IN DIVERSITY: DISCOVERING TOPICS FROM WORDS - Information Theoretic Co-clustering for Visual
Categorization
631

Table 3: Expt. Pascal VOC-2007: Comparison of information theoretic co-clustering in terms of performance gain over the
BoW model. The dataset utilized is Pacal VOC-2007. The graphs show the F
1
-score for each technique across the visual
categories in the dataset. The codebook sizes are 100, 500, and 1000.
in (Everingham, 2006). We present results for differ-
ent sizes of the topic codebook: { 100, 500, 1000 }.
The graphs show the F
1
score for different categories
in VOC-2006. The results are shown in table 2. Our
approach performs significantly better than BoW for
most of the categories and only slightly worse for a
couple of categories.
5.4 Expt: Pascal VOC 2007
In this experiment we evaluate our approach against
BoW for Pascal VOC-2007 dataset. It is the next edi-
tion in the Pascal series and has 20 categories and
more images. The categories are in four themes: per-
son; animal; indoor; vehicle. Each category contains
images ranging from 100 to 2000, with 9963 images
in all. Details can be found in (Everingham, 2007).
We present results for different sizes of the topic code-
book: { 100, 500, 1000 }. The graphs show the F
1
score for different categories in VOC-2007. The re-
sults are shown in table 3. Our approach has per-
formed remarkably better than BoW for all codebook
sizes. The inherent difference between visual cate-
gories is reflected in the graphs which show consid-
erable variation in F
1
score between different cate-
gories.
5.5 Expt: Topic Codebook Size
We want to understand the effect of the size of the
topic codebook. Accordingly in this experiment we
build topic codebook of several different sizes ranging
from 50 topics to 5000 topics. These are extreme val-
ues and performance on them should provide a bound-
ing limit on a viable topic codebook size. We evaluate
our approach against BoW and we utilize the Pascal
VOC-2010 dataset. It is a compendium of previous
editions in 2008 and 2009 as well a new images in
2010. It is considered a very challenging dataset. It
has 20 visual categories with 300 to 3500 images per
category. There are a total of 21738 images. Details
can be found in (Everingham, 2010). The codebook
sizes considered are: {50, 100, 500, 1000, 5000}. The
results are collated in table 4. The graphs show the F
1
score for different categories in VOC-2010.
6 DISCUSSION
We have presented an approach for discovering
groups of descriptor vectors scattered in feature vec-
tor space. We argued that significant intra-category
appearance variation causes descriptors sourced from
the same object part to be scattered into different parts
of feature space. The traditional approach of BoW
in unable to combine these semantically equivalent
but visually different descriptors into the same clus-
ter. Consequently, the codebook of words fails to ad-
dress the issue of intra-category variation. We ana-
lyzed the image-word joint distribution and used co-
clustering to find clusters with optimal joint distri-
butions. Our technique assigned descriptors to topic
based on both distribution in feature space and across
images. The codebook of such topics is robust to
intra-category variation and consequently performed
better than BoW. Based on different codebook sizes,
we found that a size in the range of 500 to 1000 pro-
vides the best performance. The margin of improve-
ment is bigger for more difficult datasets which is an
impressive result in favor of our approach.
ACKNOWLEDGEMENTS
This work was supported by the EPSRC project
EP/H023135/1.
REFERENCES
Boiman, O., Shechtman, E., and Irani, M. (2008). In de-
fense of nearest-neighbor based image classification.
In CVPR08, pages 1–8.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
632

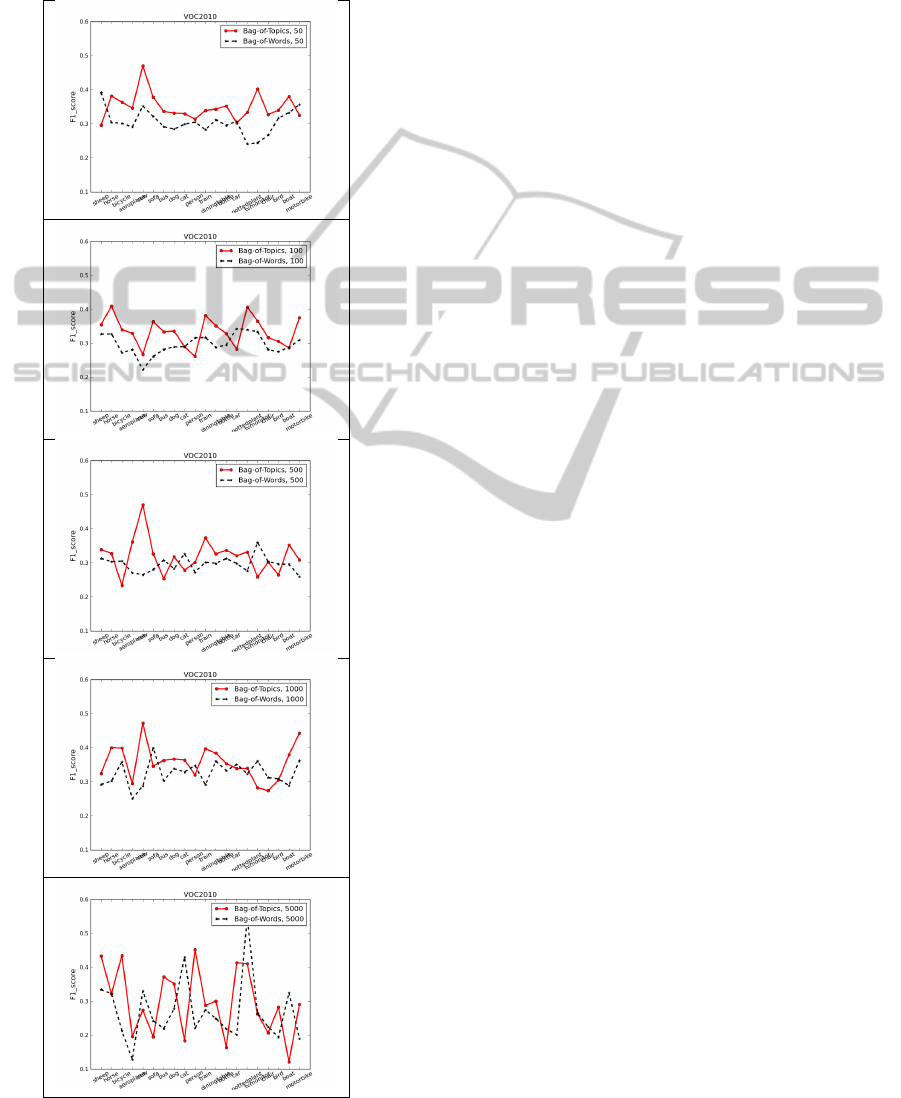
Table 4: Expt. Topic Codebook Size: Comparison of infor-
mation theoretic co-clustering in terms of performance gain
over the BoW model. The dataset utilized is Pacal VOC-
2010. The graphs show the F
1
-score for each technique
across the visual categories in the dataset. The codebook
sizes are 50, 100, 500, 1000, and 5000.
Cheng, Y. and Church, G. M. (2000). Biclustering of ex-
pression data. In Proc Int Conf Intell Syst Mol Biol.,
volume 8, pages 93–103.
Csurka, G., Dance, C. R., Fan, L., Willamowski, J., and
Bray, C. (2004). Visual categorization with bags of
keypoints. In In Workshop on Statistical Learning in
Computer Vision, ECCV, pages 1–22.
Dhillon, I. S. (2001). Co-clustering documents and words
using bipartite spectral graph partitioning. In Pro-
ceedings of the seventh ACM SIGKDD international
conference on Knowledge discovery and data min-
ing, KDD ’01, pages 269–274, New York, NY, USA.
ACM.
Dhillon, I. S., Mallela, S., and Modha, D. S. (2003).
Information-theoretic co-clustering. In In KDD, pages
89–98. ACM Press.
Everingham, M. (2006). The PASCAL Visual Object
Classes Challenge 2006 (VOC2006) Results. http://
www.pascal-network.org/ challenges/ VOC/ voc2006/
results.pdf.
Everingham, M. (2007). The PASCAL Visual Object
Classes Challenge 2007 (VOC2007) Results. http://
www.pascal-network.org/ challenges/ VOC/ voc2007/
workshop/index.html.
Everingham, M. (2010). The PASCAL Visual Object
Classes Challenge 2010 (VOC2010) Results. http://
www.pascal-network.org/ challenges/ VOC/ voc2010/
workshop/index.html.
Fei-fei, L. (2005). A bayesian hierarchical model for learn-
ing natural scene categories. In In Proc. CVPR, pages
524–531.
Gupta, A. and Bowden, R. (2011). Evaluating dimension-
ality reduction techniques for visual category recog-
nition using renyi entropy. In In Proc. of European
Signal Processing Conf., pages 913–917.
Hartigan, J. A. (1972). Direct clustering of a data ma-
trix. Journal of the American Statistical Association,
67(337):pp. 123–129.
Horster, E., Greif, T., Lienhart, R., and Slaney, M. (2008).
Comparing local feature descriptors in plsa-based im-
age models. In Proc. of the 30th DAGM symposium,
pages 446–455, Berlin, Heidelberg.
Ke, Y. and Sukthankar, R. (2004). Pca-sift: a more dis-
tinctive representation for local image descriptors. In
CVPR04, pages II: 506–513.
Liu, J. and Shah, M. (2007). Scene modeling using co-
clustering. In In Proc. ICCV, pages 1–7.
Lowe, D. (2004). Distinctive image features from scale-
invariant keypoints. International Journal on Com-
puter Vision, 60(2):91–110.
Rycroft, C. H., Grest, G. S., Landry, J. W., and Bazant,
M. Z. (2006). Analysis of granular flow in a pebble-
bed nuclear reactor. Physical Review E, 74.
UNITY IN DIVERSITY: DISCOVERING TOPICS FROM WORDS - Information Theoretic Co-clustering for Visual
Categorization
633