DICTIONARY BASED HYPERSPECTRAL IMAGE RETRIEVAL

Miguel A. Veganzones

, Mihai Datcu

and Manuel Gra˜na

Grupo de Inteligencia Computacional, Universidad del Pa´ıs Vasco, Bilbao, Spain

German Aerospace Agency (DLR), Wessling, Germany

Keywords:

Hyperspectral images, CBIR systems, Kolmogorov complexity, Dictionaries, Normalized compression

distance.

Abstract:

The normalized information distance (NID) is an universal metric distance based on Kolmogorov complexity.

However, NID is not computable in a Turing sense. The normalized compression distance (NCD) is a com-

putable distance that approximates NID by using normal compressors. NCD is a parameter-free distance that

compares two signals by their lengths after separate compression relative to the length of the signal resulting

from their concatenation after compression. The use of NCD for image retrieval over large image databases is

difﬁcult due to the computational cost of compressing the query image concatenated with every image in the

database. The use of dictionaries extracted by dictionary-based compressors, such as the LZW compression

algorithm, has been proposed to overcome this problem. Here we propose a Content-Based Image Retrieval

system based on such dictionaries for the mining of hyperspectral databases. We compare results using the

Normalized Dictionary Distance (NDD) and the Fast Dictionary Distance (FDD) against the NCD over differ-

ent datasets of hyperspectral images. Results validate the applicability of dictionaries for hyperspectral image

retrieval.

1 INTRODUCTION

Kolmogorov complexity lies in the core of algorith-

mic information theory (Chaitin, 2004; Solomonoff,

2009) that focuses on the information of individual

signals, an approach completely different to classi-

cal Shannon’s probabilistic approach to information

theory (Shannon, 2001). The normalized information

distance (NID) (Bennett et al., 1998) is an universal

metric distance based on Kolmogorov complexity (Li

and Vitanyi, 1997). However, NID is stated in terms

of Kolmogorov complexity which is uncomputable

in a Turing sense. The normalized compression dis-

tance (NCD) (Li et al., 2004) is a computable distance

that approximates NID by using normal compressors.

There has been an increasing interest in using NCD

for pattern recognition (Watanabe et al., 2002) and in

the last years NCD has been successfully applied to

different pattern recognition problems including re-

mote sensing (Cerra et al., 2010; Cerra and Datcu,

2010).

A Content Based Image Retrieval (CBIR) system

(Smeulders et al., 2000) is able to retrieve the images

stored in an image database using as image indexing

values the feature vectors extracted from the images

by means of computer vision and digital image pro-

cessing techniques. The increasing amount of Earth

Observation data provided by hyperspectral sensors,

motivates research in CBIR systems capable of min-

ing such a huge available data. There are some re-

cent works in hyperspectral CBIR systems focused on

computing the similarities between the spectral sig-

natures of the materials in the images (endmembers)

extracted by some endmember induction algorithm

(Plaza et al., 2007; Veganzones et al., 2008). The

NCD approach to pattern recognition is parameter-

free (except for the compressor’s internal parame-

ters conﬁguration) avoiding to tune up parameters to

realize operative implementations of CBIR systems.

Moreover, it does not require any feature extraction

process. However, the use of NCD in a CBIR system

demands a high computational cost due to the need of

performing the compression of the concatenations of

the query image to each of the images in the database.

The use of dictionaries (Macedonas et al., 2008; Cerra

and Datcu, 2010) has been proposed to provide an ap-

proximation to NCD when computational cost is an

issue. Thus, we propose a CBIR system based on dic-

tionaries for the mining of remote sensing large col-

lections of hyperspectral images. We compare the use

of dictionaries to the use of NCD in three datasets of

real hyperspectral images. Results validate the pro-

426

A. Veganzones M., Datcu M. and Graña M..

DICTIONARY BASED HYPERSPECTRAL IMAGE RETRIEVAL.

DOI: 10.5220/0003861904260432

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods (PRARSHIA-2012), pages 426-432

ISBN: 978-989-8425-98-0

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

posed dictionary-based hyperspectral CBIR system.

The paper is divided as follows: Sections 2 and 3

brieﬂy review the NCD and the dictionary distances,

FDD and NDD, respectively. Section 4 introduces the

proposed Dictionary-based hyperspectral CBIR sys-

tem. Section 5 presents the experimental methodol-

ogy. Section 6 gives the results. Finally, we present

some conclusions and further work in Section 7.

2 NORMALIZED COMPRESSION

DISTANCE

The conditional Kolmogorov complexity of a signal x

given a signal y, K (x|y), is the length of the shortest

program running in an universal Turing machine, that

outputs x when fed with input y. The Kolmogorov

complexity of x, K(x), is the length of the shortest

program that outputs x when fed with the empty sig-

nal λ, that is, K (x) = K (x|λ). The information dis-

tance, E (x, y), is an universal metric distance deﬁned

as the length of the shortest binary program in a Tur-

ing sense that, from input x outputs y, and from input

y outputs x. It is formulated as:

E (x, y) = max{K (x|y) , K(y|x)}. (1)

The normalized information distance, NID(x, y), is

deﬁned as:

NID(x, y) =

E (x, y)

max{K(x), K (y)}

. (2)

The NID is sometimes known as the similarity

metric due to its universality property. Here, uni-

versality means that for every admissible distance

D(x, y), the NID is minimal, E (x, y) ≤ D(x, y), up to

an additive constant depending on D but not on x and

y. However, NID(x, y) relies on the notion of Kol-

mogorov complexity which is non-computable in the

Turing sense.

The normalized compression distance,

NCD(x, y), is a computable version of (2) based

on a given compressor, C. It is deﬁned as:

NCD(x, y) =

C(xy) − min{C(x), C(y)}

max{C(x), C(y)}

(3)

where C(·) is the length of a compressed signal by

using compressor C, and xy is the signal resulting of

the concatenation of signals x and y. If the compres-

sor C is normal, then the NCD is a quasi-universal

similarity metric. In the limit case when C(·) = K (·),

the NCD(x, y) becomes “universal”. The NCD(x, y)

differs from the ideal NID(x, y)-based theory in three

aspects (Cilibrasi and Vitanyi, 2005): (a) The univer-

sality of NID(x, y) holds only for indeﬁnitely long

sequences x,y. When dealing with sequences of ﬁ-

nite length n, universality holds only for normalized

admissible distances computable by programs whose

length is logarithmic in n. (b) The Kolmogorov com-

plexity is not computable, and it is impossible to know

the degree of approximation of NCD(x, y) with re-

spect to NID(x, y). (c) To calculate the NCD(x, y)

an standard lossless compressor C is used. Although

better compression implies a better approximation to

Kolmogorov complexity, this may not be true for

NCD(x, y). A better compressor may not improve

compression for all items in the same proportion. Ex-

periments show that differences are not signiﬁcant if

the inner requirements of the underlying compressor

C are not violated.

3 DICTIONARY DISTANCES

The use of NCD (3) for CBIR entails an unafford-

ably cost due to the requirement of compressing the

concatenated signals, C(xy). To deal with this prob-

lem, we propose the use of distances based on the

codewords of the dictionaries extracted by means of

dictionary-based compressors, such as the LZW for

text strings. This dictionary approach only requires

set operations to calculate the distance between two

signals given that the dictionaries have been previ-

ously extracted. Thus, dictionary distances are suit-

able for mining large image databases where the dic-

tionaries of the images in the database can be ex-

tracted off-line.

Given a signal x, a dictionary-based compression

algorithm looks for patterns in the input sequence

from signal x. These patterns, called words, are subse-

quences of the incoming sequence. The compression

algorithm result is a set of unique words called dictio-

nary. The dictionary extracted from a signal x is here-

after denoted as D(x), with D(λ) =

0 only if λ is the

empty signal. The union and intersection of the dic-

tionaries extracted from signals x and y are denoted as

D(x∪ y) and D(x ∩ y) respectively. The dictionaries

satisfy the following properties (correspondent proofs

can be found in (Macedonas et al., 2008)):

1. Idempotency: D(x ∪ x) = D(x).

2. Monotonicity: D(x∪ y) ≥ D(x).

3. Symmetry: D(x∪ y) = D(y∪x).

4. Distributivity: D(x ∪ y) + D(z) ≤ D(x∪ z) +

D(y ∪ z).

We have found two dictionary distance functions on

the literature, the Normalized Dictionary Distance

DICTIONARY BASED HYPERSPECTRAL IMAGE RETRIEVAL

427

(NDD) (Macedonas et al., 2008) and the Fast Dictio-

nary Distance (FDD) (Cerra and Datcu, 2010):

NDD(x, y) =

D(x ∪ y) − min{D(x), D(y)}

max{D(x), D(y)}

, (4)

FDD(x, y) =

D(x) − D(x∩ y)

D(x)

. (5)

NDD and FDD are both normalized admissible dis-

tances satisfying the metric inequalities. Thus, they

result in a non-negative number in the interval [0, 1],

being zero when the compared ﬁles are equal and in-

creasing up to one as the ﬁles are more dissimilar.

4 HYPERSPECTRAL CBIR BY

DICTIONARIES

Figure 1 shows the Hyperspectral CBIR system

scheme based on dictionaries. The core of the CBIR

system is the dictionary distance between two hy-

perspectral images by means of their previously ex-

tracted dictionaries. The system interacts with a dic-

tionary database where the images dictionaries are

stored. These dictionaries have been previously ex-

tracted by off-line application of a dictionary-based

compression algorithm. System interrogation is done

using a query example approach. Firstly, the query

example is processed to extract its dictionary and sec-

ondly, it is compared to the images in the database

using the dictionary distance. A ranking of the im-

ages in the database is elaborated by ascending order

of dissimilarity (ascending distance) to the query. Fi-

nally, the system returns the k images in the database

corresponding to the ﬁrst k ranking positions, where

k is known as the query’s scope.

5 EXPERIMENTAL

METHODOLOGY

5.1 Datasets

The hyperspectral HyMAP data was made available

from HyVista Corp. and German Aerospace Center’s

(DLR) optical Airborne Remote Sensing and Calibra-

tion Facility service

. The sensed scene corresponds

to the radiance captured by the sensor in a ﬂight line

over the facilities of the DLR center in Oberpfaffen-

hofen (Germany) and its surroundings, mostly ﬁelds,

http://www.OpAiRS.aero

Figure 1: Hyperspectral CBIR based on dictionary schema.

forests and small towns. Figure 2 shows the scene

captured by the HyMAP sensor. The data cube has

2878 lines, 512 samples and 125 bands; and the pixel

values are represented by 2-bytes signed integers.

We cut the scene in patches of 64 × 64 pixels size

for a total of 360 patches forming the hyperspectral

database used in the experiments. We grouped the

patches by visual inspection in ﬁve rough categories.

The three main categories are ’Forests’, ’Fields’ and

’Urban Areas’, representing patches that mostly be-

long to one of this categories. A ’Mixed’ category was

deﬁned for those patches that presented more than one

of the three main categories, being not any of them

dominant. Finally, we deﬁned a ﬁfth category, ’Oth-

ers’, for those patches that didn’t represent any of the

above or that were not easily categorized by visual in-

spection. The number of patches per category are: (1)

Forests: 39, (2) Fields: 160, (3) Urban Areas: 24, (4)

Mixed: 102, and (5) Others: 35.

We deﬁned three datasets to validate the use of the

proposed Spectral-Spatial CBIR system in a real life

scenario. In the ﬁrst dataset we included the patches

belongingto the three main categories: Forests, Fields

and Urban Areas. In second dataset we add patches

from the fourth category: Mixed. Finally, third

dataset contains the patches from all ﬁve categories.

5.2 CBIR Performance Measures

Evaluation metrics from information retrieval ﬁeld

have been adopted to evaluate CBIR systems qual-

ity. The two most used evaluation measures are preci-

sion and recall (Smeulders et al., 2000; Daschiel and

Datcu, 2005). Precision, p, is the fraction of the re-

turned images that are relevant to the query. Recall,

q, is the fraction of returned relevant images respect

to the total number of relevant images in the database

according to a priori knowledge. If we denote T the

set of returned images and R the set of all the images

relevant to the query, then

p =

|T ∩ R|

|T|

(6)

r =

|T ∩ R|

|R|

(7)

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

428

Figure 2: Hyperspectral scene by HyMAP sensor captur-

ing the DLR facilities in Oberpfaffenhofen and its surround-

ings.

Precision and recall follow inverse trends when

considered as functions of the scope of the query.

Precision falls while recall increases as the scope in-

creases. To evaluate the overall performance of a

CBIR system, the Average Precision and Average Re-

call are calculated over all the query images in the

database. For a query of scope k, these are deﬁned as:

∑

α=1

) (8)

and

∑

α=1

). (9)

The Normalized Rank (Muller et al., 2001) is a

performance measure used to summarize system per-

formance into an scalar value. The normalized rank

for a given image ranking Ω

, denoted as Rank(H

is deﬁned as:

Rank(H

) =

∑

i=1

Ω

−

− 1)

, (10)

where N is the number of images in the dataset, N

the number of relevant images for the query H

, and

Ω

is the rank at which the i-th image is retrieved.

This measure is 0 for perfect performance, and ap-

proaches 1 as performance worsens, being 0.5 equiv-

alent to a random retrieval. The average normalized

rank, ANR, for the full dataset is given by:

ANR =

∑

α=1

Rank(H

). (11)

5.3 Methodology

We independently test the NCD (3), the NDD (4) and

the FDD (5) in three experiments corresponding to

each of the three previously deﬁned datasets. Each

hyperspectral image is ﬁrst converted to a text ﬁle in

two ways: pixel-wise and band-wise. Given that a

image in a dataset is 64× 64 pixels size and has 125

bands, in the pixel-wise ordering the text ﬁle is built

concatenating the pixels of the images in a zig-zag

way, where a pixel is a 125-components vector. In

the band-wise ordering the text ﬁle is built concate-

nating the bands of the image, where a band is re-

ordered in zig-zag to form a 64

-components vector.

The NDD and FDD are calculated using the dictio-

naries extracted by the LZW compression algorithm.

The NCD is calculated by CompLearn

software us-

ing default options, that is BZLIB compressor.

For each hyperspectral image H

in a dataset we

calculate the dissimilarity measure between H

and

http://www.complearn.org

DICTIONARY BASED HYPERSPECTRAL IMAGE RETRIEVAL

429

each of the remaining images in the dataset using a se-

lected distance. These dissimilarities are represented

as a vector s

= [s

α1

, . . . , s

αN

], where N is the number

of images in the dataset and s

α,β

is the dissimilarity

between the images H

and H

, with α, β = 1, . . . , N.

We can deﬁne the ranking of the dataset relative to the

query image, Ω

= [ω

α, p

∈ {1, . . . , N}; p = 1, . . . , N],

as the set of image indexes ordered according to in-

creasing values of their corresponding entries in the

dissimilarity vector s

. That is, we sort in increas-

ing order the components of s

, and the correspond-

ing rendering of image indexes constitute Ω

, so that

α,ω

α, p

≤ s

α,ω

α, p+1

Finally, we estimate the CBIR system perfor-

mance measures, average precision, average recall

and average normalized rank, as follows. For each hy-

perspectral image H

, a query Q

) is formulated

returning the k most similar (less dissimilar) images

in the dataset relative to the image H

, where k is

the scope of the query and takes values in the range

1 ≤ k ≤ N. The groundtruth for a query image H

a ranking, Ω

, given by the a-priori categorization

made by visual inspection. Given a query Q

the set of returned images T

) and the set of rele-

vant images V

) are deﬁned as follows:

) = Ω

α,k

α, p

s.t. s

α,ω

α, p

≤ s

α,ω

α,k

(12)

) = Ω

= [β s.t. C (β) = C (α)] (13)

where C (γ) indicates the category to which the

patch H

belongs. This way, the relevant set for a

query patch H

is formed for all those patches be-

longing to its same category C (α). Now T

) and

) can be used to calculate the average precision

and recall measures of the system, as well as the av-

erage normalized rank.

6 RESULTS

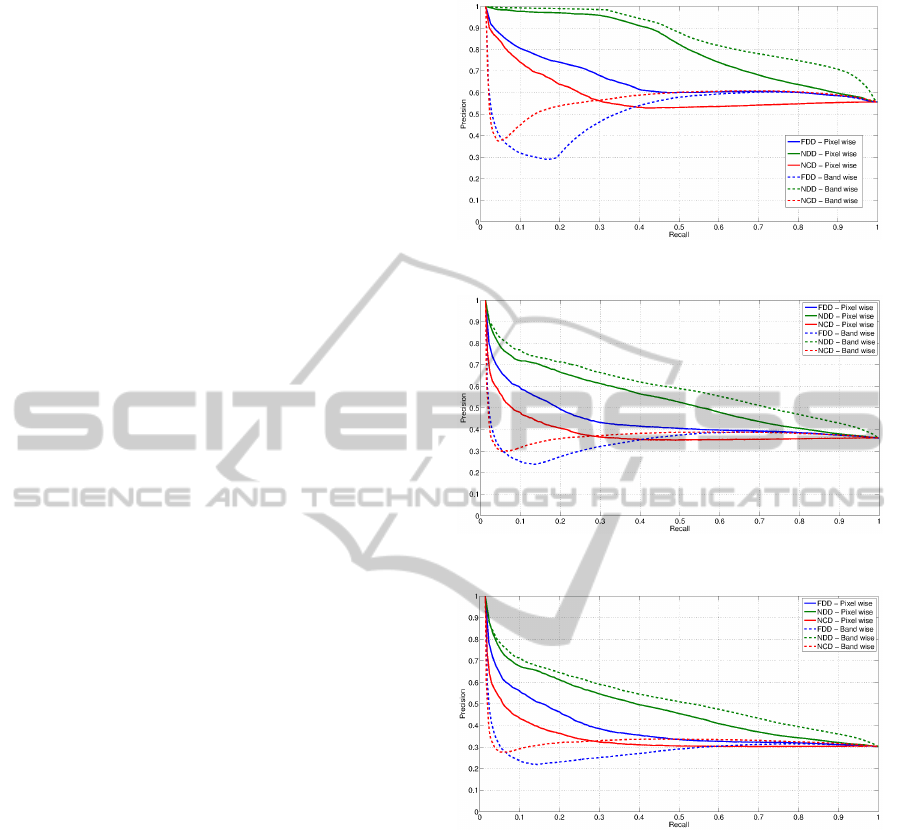
Figures 3-5 show the precision-recall curves for ex-

periments 1, 2 and 3 respectively. In each ﬁgure six

precision-recall curves are drawn, corresponding to

the three compared distances, NDD, FDD and NCD,

applied to the datasets converted into text strings us-

ing pixel-wise and band-wise orderings. In all the ex-

periments NDD outperforms the other distances inde-

pendently of the image to text string conversion or-

dering used. NCD outperforms FDD showing that

the lack of a normalization factor in the FDD is an

important issue, affecting the performance of the re-

trieval system. Furthermore, we expected the band-

wise ordering to perform better than the pixel-wise

Figure 3: Precision-recall curves for HyMAP experiment 1.

Figure 4: Precision-recall curves for HyMAP experiment 2.

Figure 5: Precision-recall curves for HyMAP experiment 3.

ordering due to the high correlation on consecutive

bands. Accordingly, the band-wise NDD gives the

best performance in all the experiments. However,

surprisingly, the band-wise ordering shows a bad per-

formance for low recall values using FDD and NCD,

improving as the recall values increase up to perfor-

mances similar to the pixel-wise ordering. In gen-

eral, the performance decreases smoothly as we in-

clude hardest categories, ’Mixed’ category in experi-

ment 2 and ’Others’ category in experiment 3, yield-

ing still good precision-recall values for the NDD

function. Also, NCD presents a general lower preci-

sion compare to dictionary-based distances, although

its performance decreases more slowly than the per-

formances of NDD and FDD as we add more difﬁcult

categories.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

430

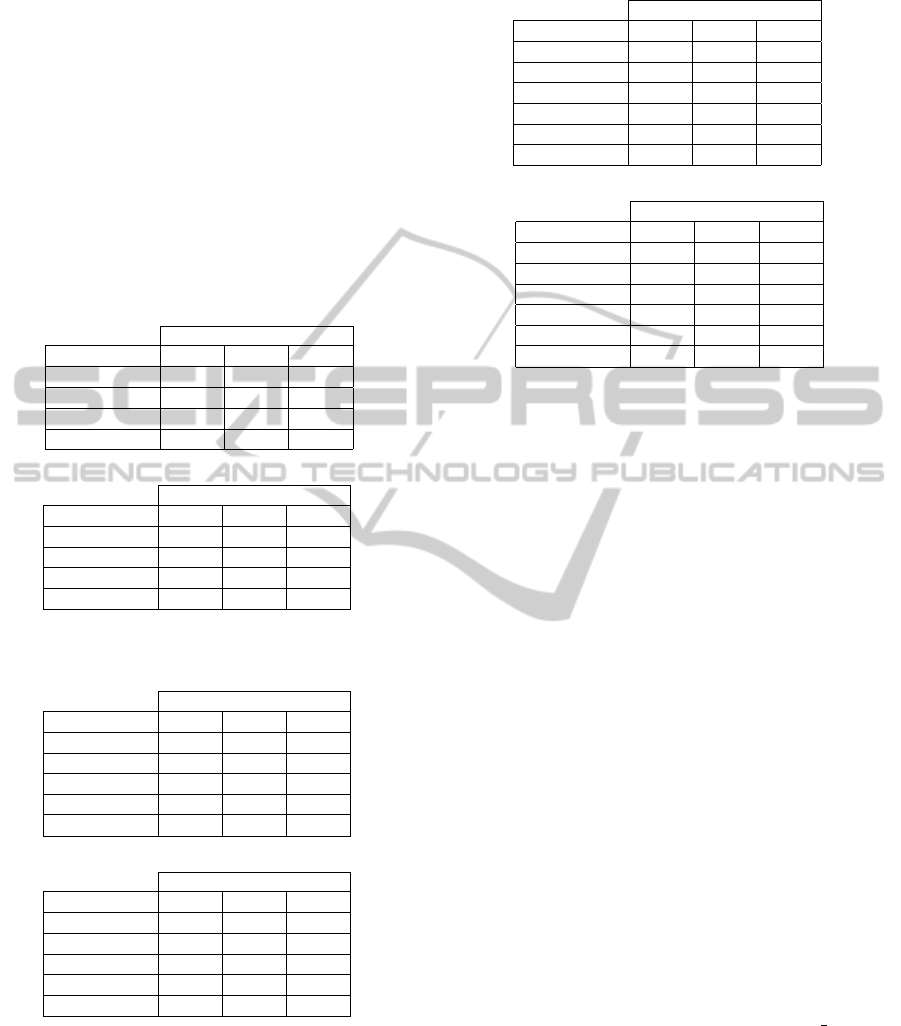
Tables 1-3 show the Average Normalized Rank

(ANR) for the experiments 1, 2 and 3 respectively.

ANR results conﬁrms the average outperform of

NDD over FDD and NCD, although FDD slightly

outperforms NDD in some cases. Interestingly, ANR

can partially explain the effect in the FDD and NCD

precision-recall curves using band-wise ordering for

low recall values, as it shows FDD is having problems

retrieving the ’Fields’ category and NCD is having

problems retrieving the ’Forests’ and ’Urban Areas’

categories. Further experiments must be conduced to

give a better explanation to why band-wise ordering

affects so much FDD and NCD performance.

Table 1: ANR results for HyMAP experiment 1.

ANR

Category FDD NDD NCD

Forests 0.015 0.010 0.129

Fields 0.143 0.090 0.180

Urban Areas 0.005 0.005 0.086

Average 0.055 0.035 0.132

(a) Pixel-wise ordering

ANR

Category FDD NDD NCD

Forests 0.073 0.014 0.292

Fields 0.159 0.038 0.118

Urban Areas 0.004 0.004 0.668

Average 0.079 0.019 0.359

(b) Band-wise ordering

Table 2: ANR results for HyMAP experiment 2.

ANR

Category FDD NDD NCD

Forests 0.069 0.053 0.168

Fields 0.283 0.210 0.299

Urban Areas 0.011 0.012 0.108

Mixed 0.223 0.236 0.311

Average 0.146 0.128 0.222

(a) Pixel-wise ordering

ANR

Category FDD NDD NCD

Forests 0.130 0.064 0.310

Fields 0.316 0.142 0.219

Urban Areas 0.005 0.006 0.681

Mixed 0.219 0.226 0.359

Average 0.167 0.109 0.392

(b) Band-wise ordering

7 CONCLUSIONS

We have introduced a Content-Based Image Retrieval

System for hyperspectral databases using dictionar-

ies. The use of a parameter-free approach based on

Table 3: ANR results for HyMAP experiment 3.

ANR

Category FDD NDD NCD

Forests 0.065 0.049 0.162

Fields 0.323 0.235 0.315

Urban Areas 0.011 0.013 0.107

Mixed 0.246 0.254 0.318

Others 0.197 0.232 0.425

Average 0.169 0.156 0.266

(a) Pixel-wise ordering

ANR

Category FDD NDD NCD

Forests 0.130 0.061 0.304

Fields 0.369 0.164 0.226

Urban Areas 0.006 0.008 0.674

Mixed 0.254 0.250 0.360

Others 0.177 0.210 0.570

Average 0.187 0.139 0.427

(b) Band-wise ordering

the Normalized Compression Distance (NCD) is not

possible due to the computational cost of compriss-

ing the query image together to each of every image

in the database. The dictionaries approach solves the

computational cost problem by approximating NCD

using dictionaries extracted ofﬂine from each of the

database images. Results using real hyperspectral

datasets show that the Normalized Dictionary Dis-

tance (NDD) outperforms the Fast Dictionary Dis-

tance (FDD) and the NCD. We also show that in or-

der to extract the dictionaries (or compress the sig-

nals for the NCD) the arrangement of the image data

in the conversion of the image to a text ﬁle affects

severelly the performance of the FDD and NCD sim-

ilarity functions. Further experiments must be con-

duced to ﬁnd an explanation of that unexpected effect.

Generally, we can conclude that the presented results

validate the use of dictionaries for hyperspectral im-

age retrieval.

ACKNOWLEDGEMENTS

The authors very much acknowledge the support of

Dr. Martin Bachmann from DLR. Miguel A. Vegan-

zones is supported by predoctoral grant BFI 07.225

from the Basque Government.

REFERENCES

Bennett, C., Gacs, P., Li, M., Vitanyi, P. M., and Zurek,

W. (1998). Information distance. Information Theory,

IEEE Transactions on, 44(4):1407–1423.

DICTIONARY BASED HYPERSPECTRAL IMAGE RETRIEVAL

431

Cerra, D. and Datcu, M. (2010). Image retrieval us-

ing compression-based techniques. In 2010 Interna-

tional ITG Conference on Source and Channel Coding

(SCC), pages 1–6. IEEE.

Cerra, D., Mallet, A., Gueguen, L., and Datcu, M. (2010).

Algorithmic information Theory-Based analysis of

earth observation images: An assessment. IEEE Geo-

science and Remote Sensing Letters, 7(1):8–12.

Chaitin, G. J. (2004). Algorithmic Information Theory.

Cambridge University Press.

Cilibrasi, R. and Vitanyi, P. (2005). Clustering by com-

pression. Information Theory, IEEE Transactions on,

51(4):1523–1545.

Daschiel, H. and Datcu, M. (2005). Information mining

in remote sensing image archives: system evaluation.

Geoscience and Remote Sensing, IEEE Transactions

on, 43(1):188–199.

Li, M., Chen, X., Li, X., Ma, B., and Vitanyi, P. (2004). The

similarity metric. Information Theory, IEEE Transac-

tions on, 50(12):3250–3264.

Li, M. and Vitanyi, P. (1997). An Introduction to Kol-

mogorov Complexity and Its Applications. Springer,

2nd edition.

Macedonas, A., Besiris, D., Economou, G., and Fotopou-

los, S. (2008). Dictionary based color image retrieval.

Journal of Visual Communication and Image Repre-

sentation, 19(7):464–470.

Muller, H., Muller, W., Squire, D. M., Marchand-Maillet,

S., and Pun, T. (2001). Performance evaluation in

content-based image retrieval: overview and propos-

als. Pattern Recognition Letters, 22(5):593–601.

Plaza, A., Plaza, J., Paz, A., and Blazquez, S. (2007). Paral-

lel CBIR system for efﬁcient hyperspectral image re-

trieval from heterogeneous networks of workstations.

In International Symposium on Symbolic and Numeric

Algorithms for Scientiﬁc Computing, 2007. SYNASC,

pages 285–291. IEEE.

Shannon, C. E. (2001). A mathematical theory of commu-

nication. SIGMOBILE Mob. Comput. Commun. Rev.,

5(1):3–55.

Smeulders, A., Worring, M., Santini, S., Gupta, A., and

Jain, R. (2000). Content-based image retrieval at the

end of the early years. Pattern Analysis and Machine

Intelligence, IEEE Transactions on, 22(12):1349–

1380.

Solomonoff, R. J. (2009). Algorithmic probability: Theory

and applications. In Information Theory and Statisti-

cal Learning, pages 1–23. Springer US, Boston, MA.

Veganzones, M. A., Maldonado, J. O., and Grana, M.

(2008). On Content-Based image retrieval systems

for hyperspectral remote sensing images. In Compu-

tational Intelligence for Remote Sensing, volume 133

of Studies in Computational Intelligence, pages 125–

144. Springer Berlin / Heidelberg.

Watanabe, T., Sugawara, K., and Sugihara, H. (2002). A

new pattern representation scheme using data com-

pression. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, 24(5):579–590.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

432