3D HUMAN BODY POSE ESTIMATION BY SUPERQUADRICS
Ilya Afanasyev, Massimo Lunardelli, Nicolò Biasi, Luca Baglivo, Mattia Tavernini, Francesco Setti
and Mariolino De Cecco
Department of Mechanical and Structural Engineering (DIMS), University of Trento, via Mesiano, 77, Trento, Italy
Keywords: Superquadrics, RANSAC Fitting, Human Body Pose Estimation, 3D Object Localization.
Abstract: This paper presents a method for 3D Human Body pose estimation. 3D real data of the searched object is
acquired by a multi-camera system and segmented by a special preprocessing algorithm based on clothing
analysis. The human body model is built by nine SuperQuadrics (SQ) with a-priori known anthropometric
scaling and shape parameters. The pose is estimated hierarchically by RANSAC-object search with a least
square fitting 3D point cloud to SQ models: at first the body, and then the limbs. The solution is verified by
evaluating the matching score, i.e. the number of inliers corresponding to a-piori chosen distance threshold,
and comparing this score with admissible inlier threshold for the body and limbs. This method can be used
for 3D object recognition, localization and pose estimation of Human Body.
1 INTRODUCTION
3D human body recognition and pose recovery are
the important problems in computer vision and
robotics with many potential applications including
motion capture, human-computer interaction, sport
and medical analysis, video surveillance, etc. The
human body pose estimation from 3D real data
obtained by a multi-camera system can be solved
different ways. A generic humanoid model
approximating a subject’s shape can use either
simple shape primitives (cylinders, cones, ellipsoids,
and superquadrics) or a surface (polygonal mesh,
sub-division surface) articulated using the kinematic
skeleton (Forsyth, et al., 2005; Moeslund, et al,
2006; Balan, et al. 2007; Mun Wai Lee and Cohen,
2004; Ivecovic and Trucco, 2006). We consider
below only “Direct-model-use” pose estimation
approach corresponding to an explicit 3D geometric
representation of human shape and kinematic
structure by SQ.
Some authors propose recovering a pose with a
shape detection stage (by hierarchical exemplar
matching in the individual camera views with 3D
upper body model based on tapered SQ), combining
with Viterbi-style best trajectory estimation, and a
filtering approach to 3D model texturing (Hofmann
and Gavrila, 2009). Other authors used a method for
restoring 3D human body motion from monocular
video sequences based on a robust image matching
metric, incorporation of joint limits and non-self-
intersection constraints, and a sample-and-refine
search guided by rescaled cost-function covariance
(Sminchisescu and Triggs, 2003). There is also a
method for recovering an object by SQ models with
the recover-and-select paradigm, filling range
images with a set of seeds (small SQ models), and
increasing these seeds with a growth iteration
approach selecting the suitable models. This
approach was tried out on a wooden mannequin
(Jaklic et al., 2000; Leonardis et al., 1997).
We propose using the hierarchical RANSAC-
based model-fitting technique with a composite SQ
model of human body and limbs. It is known that SQ
models permit to describe complex-geometry objects
with few parameters and generate simple
minimization function to estimate an object pose
(Jaklic et al., 2000 and Leonardis et al., 1997). We
assume the body shape and dimensions are known a-
priori to model body and limbs by SQ with correct
anthropometric parameters in the metric coordinate
system. The logic of our 3D Human Body pose
estimation algorithm is presented by the block
diagram (Figure 1). The object pose estimation starts
with pre-processing of the 3D point cloud captured
by multiple cameras. The preprocessing stage
realizes segmentation of the Human Body into 9
parts (body, arms, forearms, hips and legs). After
that the algorithm recovers 3D position of the body
as the largest object (“Body Pose Search”) and then
294
Afanasyev I., Lunardelli M., Biasi N., Baglivo L., Tavernini M., Setti F. and De Cecco M..
3D HUMAN BODY POSE ESTIMATION BY SUPERQUADRICS.
DOI: 10.5220/0003862202940302
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 294-302
ISBN: 978-989-8565-04-4
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

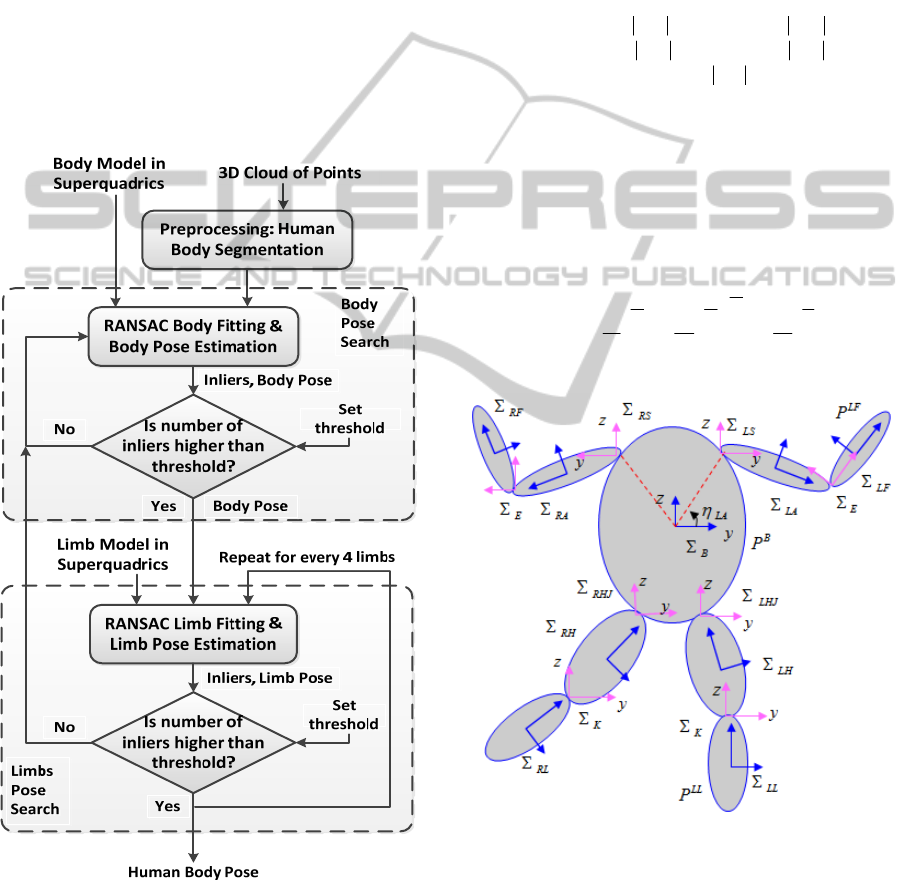
uses the information about body position to restore
human limbs poses (“Limbs Pose Search”). To cope
with measurement noise and outliers, the object pose
is estimated by RANSAC-SQ-fitting technique. We
control the fitting quality by setting inlier thresholds
for limbs (body). These thresholds are a ratio of the
optimal amount of inliers to whole data points of the
corresponding limb (body). The tests showed that as
a result of the Body Pose Search we can obtain a
hypothesis with a slightly wrong body position,
which can satisfy a body threshold, but can’t be
applied to overcome limb thresholds. For this
reason, when the limb inliers solution less than a
limb threshold, the algorithm restarts the Body Pose
Search until finding suitable results of RANSAC-
SQ-fitting for every limbs.
Figure 1: The block diagram of 3D Human Body Pose
Estimation algorithm.
2 SUPERQUADRICS MODEL OF
THE HUMAN BODY
2.1 SuperQuadric parameters
It is known (Jaklic et al., 2000 and Leonardis et al.,
1997) that the explicit form of the parametric
equation of the superquadrics, which is usually used
for SQ representation and visualization, is:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅⋅
⋅⋅⋅⋅
⋅⋅⋅⋅
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
1
21
21
sin)(sin
sin)(sincos)(cos
cos)(coscos)(cos
3
2
1
ε
εε
εε
ηη
ωωηη
ωωηη
signuma
signumsignuma
signumsignuma
z
y
x
(1)
where x, y, z – superquadric coordinate system;
a
1
, a
2
, a
3
– scale parameters of the object;
ε
1
, ε
2
– object shape parameters;
η, ω – spherical coordinates.
The implicit superquadric equation is more suitable
for mathematical modeling to do fitting 3D data:
()
1
1
2
22
2
3
2
2
2
1
,,
ε
ε
ε
εε
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
a
z
a
y
a
x
zyxF

(2)
Figure 2: Presentation of Human Body in 9 parts: B –
body, LA/RA – Left/Right Arms, LF/RF – Left/Right
Forearms, LH/RH – Left/Right Hips, LL/RL – Left/Right
Legs. Other abbreviations: LS – Left Shoulder, E – Elbow,
η
LA
– angle position of Left Shoulder, LHJ – Left Hip
Joint, K – Knee, etc.
The object under investigation is the Human
Body (Figure 2), which consists of 9 superquadrics –
3D HUMAN BODY POSE ESTIMATION BY SUPERQUADRICS
295

superellipsoids with the shape parameters ε
1
= ε
2
=
0.5 and the following scaling parameters for
different parts of the body:
- Body: a
1
= 0.095, a
2
= 0.18, a
3
= 0.275 (m).
- Arms: a
1
= a
3
= 0.055, a
2
= 0.15 (m).
- Forearms: a
1
= a
3
= 0.045, a
2
= 0.13 (m).
- Hips: a
1
= a
2
= 0.075, a
3
= 0.2 (m).
- Legs: a
1
= a
2
= 0.05, a
3
= 0.185 (m).
The scale parameters of SQ are presented in the
metrical superquadric object-centered coordinate
systems.
2.2 Human Body in SQ
The position of Human Body is defined by the
following rotation & translation sequences of the
Body Superquadrics:
1. Translation of center of BODY (x
c
, y
c
, z
c
), along
x, y, z-coordinates.
2. Rotation α among x (clockwise).
3. Rotation β among y (clockwise).
4. Rotation γ among z (clockwise).
The rotation matrix of BODY R
BODY
is:
() ()
() ()
() ()
() ()
() ()
() ()
10 0 0
cos 0 sin 0 cos sin 0 0
0cos sin 0
0100
sin cos 0 0
0sin cos 0 sin 0cos 0
0010
00 0 1 0 001 0 0 01
R
BODY
ββ γγ
αα
γγ
αα β β
−
⎡⎤⎡⎤⎡⎤
⎢⎥⎢⎥⎢⎥
−
=⋅⋅
⎢⎥⎢⎥⎢⎥
−
⎢⎥⎢⎥⎢⎥
⎣⎦⎣⎦⎣⎦
(3)
The transformation matrix T
BODY
for the BODY is:
.
1000
100
010
001
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅=
c
c
c
BODYBODY
z
y
x
RT

(4)
2.3 Human Arms and Forearms in SQ
Let’s consider the transformation equations for Left
Arm and Forearm.
The position of Left Shoulder according to the
center of the body coordinate system (Figure 2) is
estimated by SQ explicit equation (1):
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅⋅
⋅⋅=
⎟
⎠
⎞
⎜
⎝
⎛
===
1
1
sin)(sin
cos)(cos
0
2
,
3
2
ε
ε
ηη
ηη
π
ωηη
signuma
signumaPP
LA
B
S
(5)
Taking into account (5), the transformation Body
- Left Shoulder (B-LS) will be:
.
1000
100
010
001
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
"
"
B
S
B
LS
P
T

(6)
We can express the transformation: Left
Shoulder - Left Arm (LS-LA) by the following
rotation & translation sequences:
1. Rotation α among x (clockwise).
2. Rotation β among z (anticlockwise).
3. Rotation γ among y (clockwise).
4. Translation of SQ center on distance a
2
along y.
()
,
1000
0100
010
0001
,,
2
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅=====
a
RTT
LALALALA
LS
LA
LS
LA
γγββαα

(7)
where R
LA
is the rotation matrix of Left Arm:
() ()
() ()
(
)
(
)
() ()
(
)
(
)
() ()
10 0 0
cos sin 0 0 cos 0 sin 0
0cos sin 0
0100
sin cos 0 0
.
0sin cos 0 sin 0cos 0
0010
00 0 1 0 001 0 001
LA
R
ββ γ γ
αα
ββ
αα γ γ
⎡
⎤⎡ ⎤⎡ ⎤
⎢
⎥⎢ ⎥⎢ ⎥
−
−
=⋅⋅
⎢
⎥⎢ ⎥⎢ ⎥
−
⎢
⎥⎢ ⎥⎢ ⎥
⎣
⎦⎣ ⎦⎣ ⎦
(8)
The transformation Left Arm - Elbow (LA-E) is
.
1000
0100
010
0001
2
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
a
T
LA
E

(9)
The transformation Elbow - Left Forearm (E-LF) is
created by
1. Rotation δ
LF
among x (clockwise).
2. Translation of SQ center on -a
2
along y.
()
() ()
() ()
1
2
10 0 0
0cos sin
.
0sin cos 0
00 0 1
EE
LF LF LF
a
TT
δδ
δδ
δδ
−
⎡
⎤
⎢
⎥
−
===
⎢
⎥
−
⎢
⎥
⎣
⎦

(10)
Finally, taking into account equations (5)-(10),
the full transformation for every point of system
“Body - Left Forearm” (B-LF) can be calculated this
way:
() .
,
1
BE
LF
LA
E
LS
LA
B
LS
LF
LFE
LF
LA
E
LS
LA
B
LS
B
PTTTTP
PTTTTP
⋅⋅⋅⋅=
⋅⋅⋅⋅=
−

(11)
where P
B
, P
LF
- coordinates of Body and Left
Forearm points correspondingly (Figure 2).
The main equations for Right Arm and Forearm
are calculated the same way.
2.4 Human Hips and Legs in SQ
Analogically with previous equations (Section 2.3),
the full transformation for every point of system
“Body - Left Leg” (B-LL) is calculated this way:
() .
,
1
BK
LL
LH
K
LHJ
LH
B
LHJ
LL
LLK
LL
LH
K
LHJ
LH
B
LHJ
B
PTTTTP
PTTTTP
⋅⋅⋅⋅=
⋅⋅⋅⋅=
−

(12)
where P
B
, P
LL
– coordinates of Body and Left Leg
points respectively (Figure 2);
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
296

T – corresponding transformations (13)-(16).
The transformation Body – Left Hip Joint (B-
LHJ) is absolutely the same as T
LS
B
from equation
(6), except using the angle η
LL
in the equation (5) for
calculation of the Left Hip position.
The transformation Left Hip Joint – Left Hip
(LHJ-LH) uses other rotation sequences and
translation if compare with equations (7) and (8):
1. Rotation α among x (clockwise).
2. Rotation β among y (anticlockwise).
3. Rotation γ among z (clockwise).
4. Translation of SQ center on distance -a
3
along z.
()
,
1000
100
0010
0001
,,
3
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⋅=====
a
RTT
LHLHLHLH
LHJ
LH
LHJ
LH
γγββαα

(13)
where R
LH
is the rotation matrix of Left Hip:
() ()
() ()
(
)
(
)
() ()
(
)
(
)
() ()
10 0 0
cos 0 sin 0 cos sin 0 0
0cos sin 0
01 0 0
sin cos 0 0
.
0 sin cos 0 sin 0 cos 0
0010
00 0 1 00 0 1 0 0 01
LH
R
ββγγ
αα
γγ
αα β β
−−
⎡⎤⎡⎤⎡⎤
⎢⎥⎢⎥⎢⎥
−
=⋅⋅
⎢⎥⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥
⎣⎦⎣⎦⎣⎦
(14)
The transformation Left Hip - Knee (LH-K) is
.
1000
100
0010
0001
3
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
a
T
LH
K

(15)
The transformation Knee - Left Leg (E-LL) is
created by
1. Rotation δ
LL
among y (clockwise).
2. Translation of SQ center on a
3
along z.
()
() ()
() ()
1
3
cos 0 sin 0
01 0 0
.
sin 0 cos
00 0 1
KK
LL LL LL
TT
a
δδ
δδ
δδ
−
−
⎡⎤
⎢⎥
===
⎢⎥
⎢⎥
⎣⎦

(16)
The similar transformations for Right Hip and
Leg are described by almost the same equations.
3 3D HUMAN BODY FITTING
ALGORITHM
3.1 About Sensors, Object and Data
The 3D point cloud is captured with a multi-camera
system developed at the University of Trento in the
framework of the project VERITAS (De Cecco,
Paludet, et al., 2010). The multi-camera system for
acquiring range images consists of 8 pairs of
cameras, which are a multiple stereo system, like a
multi-camera system described in the paper (De
Cecco, Pertile, et al., 2010), employing
measurements a 3D-surface with superimposed
colored markers.
The multi-camera system gives 3D video of
Human Body movement consisted of 119 frames,
but we are analyzing every frame separately. The
total amount of 3D Human Body data points for
single 3D video frame is more than 2100.
3.2 Preprocessing: Segmentation
The segmentation of 3D point cloud of a human body
has been done automatically basing on the clothing
analysis. We extract the human being clusters (body
and eight limbs: left/right arms, forearms, hips and
legs) according to the special clothing marks on the
garment (Figure 6). These marks generate color
structures, which are pre-defined clothing models.
The result of this clothing analysis is a segmentation
matrix, the elements of which set belonging to the
definite limbs of the body for every data points.
Experimental results show that such clothing
segmentation is well-able to extract limbs of human
body from range images with variations in
background environment and lighting conditions.
The segmentation is completed with the use of
RANSAC fitting. The markers near to the body
joints have uncertain association with limbs. This
uncertainty can be solved using RANSAC-SQ-
fitting. As the result of this clothing segmentation
we have approximately 800 data points of the body,
30-70 points of left/right arms, 15-25 points of
forearms, 300-600 points of hips, and 80-150 points
of legs (Figures 6 and 7).
This method will also work with any 3D point
cloud data acquired by other sensors (for example
Kinect) with following segmentation of body parts
from single depth images invariantly to body
clothing, as an example, using randomized decision
forests (Shotton J., et al., 2011).
3.3 RANSAC Algorithm
We use RANSAC ("RANdom SAmple Consensus")
algorithm in estimating 3D Body and Limb Poses
with SQ Model Fitting. To remind the basic concept
of RANSAC algorithm, Figure 3 presents the
pseudocode of RANSAC algorithm based on Peter
Kovesi software (Kovesi, 2008). The number of
iterations performed by RANSAC (the parameter k)
can be determined from the following formula:
3D HUMAN BODY POSE ESTIMATION BY SUPERQUADRICS
297

log(1 )
.
log 1
s
p
k
inliers
n
−
=
⎛⎞
⎛⎞
−
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠

(17)
where p – is the probability desired for choosing
at least one sample free from outliers (in most of
applications: p=0.99);
s – is a number of points required to fit the
model.
The success of RANSAC usage depends on
choosing the right models. In our case it means
correct choice of SQ parameters (as anthropometric
sizes of human body and limbs) and logic of
recognition (i.e. the sequence of body/limbs fitting).
The attempt of one stage RANSAC recognition
whole parts of human body simultaneously will be
failed because of big amount of outliers. The test
showed that an acceptable quality of RANSAC-SQ-
fitting can be achievable by hierarchical human body
pose estimation (Figure 1).
3.4 RANSAC Model Fitting
The Body and Limbs Pose Search stages of the
algorithm are very similar and have common logic
and functions (Figure 1). The logic of RANSAC-
SQ-fitting algorithms both for the body and a limb
are explained by pseudocodes (Figures 4 and 5).
Let’s consider the RANSAC Body Fitting
algorithm. We are using the RANSAC-based Object
Search to find the body pose hypothesis, i.e. 6
variables: 3 angles of rotation (α, β, γ) and 3
translation coordinates (x
C
, y
C
, z
C
). Having these
variables we can calculate the transformation matrix
T
BODY
(4). We are fitting a model described by the
superquadric implicit equation (2) to 3D data of the
known object (i.e. the points of the body sorted by
segmentation). Each RANSAC sample calculation is
started by picking a set of random points (s = 6
points for Body fitting, which are the minimal
number of points to calculate the SQ position) from
3D datapoints in the world coordinate system (x
Wi
,
y
Wi
, z
Wi
). To transform these points to the
superquadric centered coordinate system (x
Si
, y
Si
, z
Si
),
we use the following equation:
,
1
),,(
1
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅=
−
i
i
i
iiii
w
w
w
BODYssss
z
y
x
TzyxF

(18)
where
1−
BODY
T
is the inverting homogeneous
transformation matrix of the body (4).
Then we are calculating the inside-outside
function according to the superquadric implicit
equation (2) in world coordinate system:
.
)()()(
1
1
2
22
2
3
2
2
2
1
ε
ε
ε
εε
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
a
zF
a
yF
a
xF
F
iii
i
ssssss
w

(19)
It is easy to see that the inside-outside function
for superquadrics has 11 parameters (Jaklic et al.,
2000; Solina, 1990):
),,,,,,,,,,,,,,(
21321 cccWWWw
zyxaaazyxFF
iiii
χ
β
α
ε
ε
=

(20)
where 5 parameters of the superquadric size and
shape are known (a
1
, a
2
, a
3
, ε
1
, ε
2
) and other 6
parameters (α, β, γ, x
C
, y
C
, z
C
) represent the
orientation and position of superquadrics in space
and should be found by minimizing the cost-
function:
(
)
,1)(min
2
1
2
1
−=
∑
=
ε
i
W
w
s
i
ii
F
FxF

(21)
where additional exponent ε
1
ensures that the points
of the same distance from SQ surface have the same
values of F
W
(Solina and Bajcsy, 1990).
So we are fitting SQ model to this random
dataset by minimizing an inside-outside function of
distance to SQ surface (applying the “Trust-Region
algorithm” or “Levenberg-Marquardt algorithm” in
the nonlinear least-square minimization method).
After this we are evaluating amount of inliers by
comparing the distances between every point of 3D
point cloud and SQ model with assigned distance
threshold t (to accelerate the calculations we took
the distance threshold t = 2 cm):
(
)
.1
2
321
1
−⋅⋅⋅=
ε
i
wi
Faaad

(22)
Analogically, we are realizing the RANSAC
Limb Fitting (Figure 5). Let’s consider the example
of the Limb Fitting of
Left Arm (LA) and Forearm
(LF). The main differences between RANSAC Body
and Limb Fitting are:
- in the minimal number of points to calculate the
SQ position for Limb fitting s = 3 (although we need
to set the body transform matrix T
BODY
, obtained
from the Body Fitting algorithm).
- in using 4 variables for Limbs Pose Search: 4
angles of rotation (α, β, γ, δ) equations (8,10).
- in minimizing the joint cost-function of two
superquadrics together, considering two limbs
simultaneously:
(
)( )
11
2
2
() ()
1
min ( ) 1 1 ,
LA LF
ii
W
s
ii wLA wLF
F
i
Fx F F
εε
=
⎡
⎤
=−⋅−
⎣
⎦
∑

(23)
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
298

where abbreviations LA and LF mean that
parameters and variables are related to the Left Arm
(LA) and Forearm (LF) Limbs correspondingly.
Figure 3: Pseudocode of RANSAC algorithm.
To speed up the fitting process, the position of
initial starting point of minimization searching in
world coordinates can be chosen in the center of
gravity of the body. Thus SQ modeling allows to
recovery an object in “clouds of points” with using
the limited number of 3D data points. The
minimization process with “Trust-Region” or
“Levenberg-Marquardt” algorithms is stable without
Figure 4: Pseudocode of RANSAC Body Fitting
algorithm.
Algorithm RANSAC
_
Body
_
Fitting (x,t)
s = 6; % min number of points to fit a SQ
t = 2·10
-2
; % a threshold: datapoint-SQ (2 cm)
% Trials - a number of iterations in algorithm
% x - a dataset x
n
of n points of a body, which
are a vector of the world coordinates
),,(
iii
www
zyx

% fittingfn - function to define SQ position by s, x.
function fittingfn (x
s
)
set x
0
s
= 0; % initial values of α,β,γ,x
c
,y
c
,z
c
set SQ
BODY
parameters a
1
-a
3
,ε
1
,ε
2
for all x
i
from x
n
() ()
() ()
(
)()
() ()
() ()
() ()
.
1000
100
010
001
1000
0100
00cossin
00sincos
1000
0cos0sin
0010
0sin0cos
1000
0cossin0
0sincos0
0001
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
c
c
c
BODY
z
y
x
T
γγ
γγ
ββ
ββ
αα
αα
;
1
),,(
1
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅=
−
i
i
i
iiii
w
w
w
BODYssss
z
y
x
TzyxF
;
)()()(
1
1
2
22
2
3
2
2
2
1
ε
ε
ε
εε
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
a
zF
a
yF
a
xF
F
iii
i
ssssss
w
(
)
.1)(min
2
1
2
1
−=
∑
=
ε
i
w
w
s
i
ii
F
FxF
end for
calculate variables α,β,γ,x
c
,y
c
,z
c
by minimizing
∑
=
s
i
ii
xF
1
2
)(min

return T
BODY
% distfn - a function to select distances from SQ to x
function
distfn (T
BODY
, x)
for all x
i
from x
n
;
1
),,(
1
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅=
−
i
i
i
iiii
w
w
w
BODYssss
z
y
x
TzyxF

;
)()()(
1
1
2
22
2
3
2
2
2
1
ε
ε
ε
εε
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
a
zF
a
yF
a
xF
F
iii
i
ssssss
w
(
)
.1
2
321
1
−⋅⋅⋅=
ε
i
wi
Faaad

if d
i
< t then x
i
= inliers
end for
return inliers
Trials = 1000; % a number of iterations
start RANSAC (x, fittingfn, distfn, s, t, Trials)
return bestT
BODY
, bestinliers
Algorithm RANSAC (x, fittingfn,
distfn, s, t, Trials)
% x - a dataset x
n
of n observations
% fittingfn - a function that fits a model to x
% distfn - a function that checks a distance
from a model to x
% s - min number of data to fit the model M
% t – a threshold (a distance: datapoint - model)
% Trials - a number of iterations in algorithm
iter := 0 % count of iterations
bestM := 0 % the best model
inliers := 0 % accumulator for inliers
score := 0 % amount of inliers
p := 0.99 % probability of a sample
without outliers
while k > iter
% randomly selected j values from data x
n
x
j
s
:= random(x
n
);
% model parameters, which fitted to x
j
s
M := fittingfn(x
j
s
);
for all x
i
from x
n
if distfn(M, x
i
n
) < t
inl
k
:= x
i
end if
end for
% amount of inliers
m := length(inl
m
);
% the test to check how good the model is
if m > score
score := m; % amount of inliers
inliers := inl; % inliers
bestM := M; % the best model
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
s
n
inliers
p
k
1log
)1log(

end if
increment iter
if iter > Trials
break
end if
end while
3D HUMAN BODY POSE ESTIMATION BY SUPERQUADRICS
299

Figure 5: Pseudocode of RANSAC Limb Fitting algorithm
on example of Left Arm (LA) and Forearm (LF) Limbs.
redundant complexity and time consuming. The
Figures 6 and 7 show the result of fitting by the
RANSAC-SQ-Fitting algorithm (pink points –
inliers, cyan – outliers). For most of 3D video
frames, the amount of inliers is more than 65% from
approximately 2100 points of 3D rawdata.
Figure 6: Illustration of RANSAC Limb Fitting algorithm.
At the top: left – a pose of a human in the garment, right –
“cloud of points”. At the bottom: left – the result of
RANSAC-fitting to 3D data (pink points – inliers, cyan –
outliers), right – final pose estimation.
The small amount of data points for arms and
forearms (Section 3.2) gives some displacements of
the upper limbs poses from one 3D video frame to
another. It spoils the impression of the Human Body
movement when we are preparing 3D video
collecting together 3D Human body models from the
individual video frames processed by RANSAC-SQ-
fitting. This problem can be solved in future by
Algorithm RANSAC_Limb_Fitting (x,t)
s = 3; % min number of points to fit a SQ
t =
2·10
-2
; % a threshold: datapoint-SQ (2 cm)
set T
BODY
; % from Body Fitting Algorithm
% x - a dataset x
n
of n points of a limb, which are
a vector of the world coordinates
),,(
iii
www
zyx

% fittingfn - function to define SQ position by s, x.
function fittingfn (x, T
BODY
)
set x
0
s
= 0; % initial values of α,β,γ,δ
set a
1
-a
3
,ε
1
,ε
2
for SQ
LA
and SQ
LF
set η
LA
; % the angle position of a Shoulder
for all x
i
from x
n
;
LS
LA
BODY
LSBODY
LA
TTTT
LIMB
⋅⋅= ;
E
LF
LA
E
LS
LA
BODY
LSBODY
LF
TTTTTT
LIMB
⋅⋅⋅⋅=
()
()
()
1
2
1
3
100 0
010 cos
;
001 sin
000 1
B
BODY
LA
LS LA
B
LA
a
T
a
ε
ε
η
η
η
⎡⎤
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
⎣⎦
2
100 0
010
;
001 0
000 1
LA
LS
LA LA
a
TR
⎡⎤
⎢⎥
=⋅
⎢⎥
⎢⎥
⎣⎦
() ()
() ()
(
)
(
)
() ()
(
)
(
)
() ()
10 0 0
cos sin 0 0 cos 0 sin 0
0cos sin 0
0100
sin cos 0 0
.
0sin cos 0 sin 0cos 0
0010
00 0 1 0 001 0 001
LA
R
ββ γ γ
αα
ββ
αα γ γ
⎡⎤⎡⎤⎡⎤
⎢⎥⎢⎥⎢⎥
−
−
=⋅⋅
⎢⎥⎢⎥⎢⎥
−
⎢⎥⎢⎥⎢⎥
⎣⎦⎣⎦⎣⎦
2
100 0
010
;
001 0
000 1
LA
LA
E
a
T
⎡⎤
⎢⎥
=
⎢⎥
⎢⎥
⎣⎦
()
() ()
() ()
2
1
10 0 0
0cos sin
.
0sin cos 0
00 0 1
LF
EE
LF LF LF
a
TT
δδ
δδ
δδ
−
⎡⎤
⎢⎥
−
===
⎢⎥
−
⎢⎥
⎣⎦

()
1
(, ,) ;
1
i
i
iiii LIMB
i
w
LA LA
w
ssss
w
x
y
Fxyz T
z
−
⎡⎤
⎢⎥
=⋅
⎢⎥
⎢⎥
⎣⎦
()
1
(, ,) ;
1
i
i
iiii LIMB
i
w
LF LF
w
ssss
w
x
y
Fxyz T
z
−
⎡⎤
⎢⎥
=⋅
⎢⎥
⎢⎥
⎣⎦

2
1
22 1
22 2
12 3
() () ()
;
ii i
i
ss ss ss
w
Fx Fy Fz
F
aa a
ε
ε
ε
εε
⎛⎞
⎛⎞⎛⎞⎛⎞
⎜⎟
=+ +
⎜⎟⎜⎟⎜⎟
⎜⎟
⎝⎠⎝⎠⎝⎠
⎜⎟
⎝⎠
()()
11
2
2
() ( )
1
min ( ) 1 1 .
LA LF
ii
W
s
ii wLA wLF
F
i
Fx F F
εε
=
⎡⎤
=−⋅−
⎣⎦
∑

end for
calculate variables α,β,γ,δ by
minimizing
∑
=
s
i
ii
xF
1
2
)(min

return α,β,γ,δ
% distfn - a function to select distances from SQ to x
function distfn (x,T
BODY
,α,β,γ,δ)
for all x
i
from x
n
()
1
(, ,) ;
1
i
i
iiii LIMB
i
w
LA LA
w
ssss
w
x
y
Fxyz T
z
−
⎡⎤
⎢⎥
=⋅
⎢⎥
⎢⎥
⎣⎦
()
1
(, ,) ;
1
i
i
iiii LIMB
i
w
LF LF
w
ssss
w
x
y
Fxyz T
z
−
⎡⎤
⎢⎥
=⋅
⎢⎥
⎢⎥
⎣⎦

2
1
22 1
22 2
12 3
() () ()
;
ii i
i
ss s s ss
w
Fx Fy Fz
F
aa a
ε
ε
ε
εε
⎛⎞
⎛⎞⎛⎞⎛⎞
⎜⎟
=+ +
⎜⎟⎜⎟⎜⎟
⎜⎟
⎝⎠⎝⎠⎝⎠
⎜⎟
⎝⎠
()
1
2
123
1.
i
iw
daaaF
ε
=⋅⋅⋅ −

if d
i
< t then x
i
= inliers
end for
return inliers
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
300

correcting 3D Human Body Pose Estimation
algorithm or improving 3D data point acquisition
process, or using other sensors (for example MS
Kinect) and other segmentation techniques
4 RESULTS
The Figures 6 and 7 show the workability of the
RANSAC-SQ-fitting algorithm for tasks of Human
Body Pose Estimation. For most of 3D video frames,
the amount of inliers is more than 65% from
approximately 2100 points of 3D rawdata.



Figure 7: Illustration of RANSAC Limb Fitting algorithm.
At the top: left – a pose of a human in the garment, right –
“cloud of points”. At the bottom: left – the result of
RANSAC-fitting to 3D data (pink points – inliers, cyan –
outliers), right – final pose estimation.
The small amount of data points for the upper
limbs gives some limb pose displacements and
spoils the impression from body movement if
collecting back 3D video from single frames.
This problem can be solved in future by
correcting 3D Human Body Pose Estimation
algorithm, or improving 3D data point acquisition
process, or using other sensor and segmentation
techniques.
The algorithm has been developed in MATLAB.
3D data have been captured from a multi-camera
system and then processed offline. The pose
estimation technique described has been tested at
processing 3D video of Human Body movement
consisted of 119 frames giving encouraging results.
The presence of loops in the algorithm (during the
hierarchical Body and Limbs Pose searches) can be
a problem for real-time body movement application.
But the correct comparative evaluation of speed and
accuracy of the body pose estimation can be realized
in the future if a) use other pose recognition methods
with the existing multicamera system, or b) apply
the proposed method with another sensor.
5 CONCLUSIONS
This paper describes a method of Human Body pose
estimation from 3D real data obtained by a multi-
camera system and structured by the special clothing
analysis. This method will also work with any 3D
point cloud data acquired by other sensors and
segmented using any other algorithms.
The human body was modeled by a composite
SuperQuadric (SQ) model presenting body and
limbs with correct a-priori known anthropometric
dimensions. The proposed method based on
hierarchical RANSAC-object search with a robust
least square fitting SQ model to 3D data: at first the
body, then the limbs. The solution is verified by
evaluating the matching score (the number of inliers
corresponding to a-piori chosen distance threshold),
and comparing this score with admissible inlier
threshold for the body and limbs.
This method can be useful for applications dealt
with 3D Human Body recognition, localization and
pose estimation.
ACKNOWLEDGEMENTS
The work of Ilya Afanasyev on creating the
algorithms of 3D object recognition and pose
estimation has been supported by the grant of
3D HUMAN BODY POSE ESTIMATION BY SUPERQUADRICS
301

EU\FP7-Marie Curie-COFUND-Trentino postdoc
program, 2010-2013. 3D data acquisition and
segmentation were executed in the framework of
project VERITAS funded by FP7, EU. Francesco
Setti was supported by the European Commission
and Provincia Autonoma di Trento under Marie
Curie Action – COFUND project ABILE. The
authors are very grateful to colleagues from
Mechatronics dep., UniTN, namely Alberto Fornaser
for his help and support of 3D data acquisition.
REFERENCES
Balan A., Sigal L., Black M., Davis J., and Haussecker H.,
2007. Detailed Human Shape and Pose from Images.
In IEEE Conf. Proc. CVPR '07. DOI:
10.1109/CVPR.2007.383340.
De Cecco M., Pertile M., Baglivo L., Lunardelli M., Setti
F., and Tavernini M., 2010. A unified framework for
uncertainty, compatibility analysis, and data fusion for
multi-stereo 3-D shape estimation. In IEEE
Transactions on Instrumentation and measurement,
Vol. 59, No. 11.
De Cecco M., Paludet A., Setti F., Lunardelli M., Bini R.,
Tavernini M., Baglivo L., Kirchner M., Da Lio M.,
2010. VERITAS poster at SIAMOC congress, Italy.
http://veritas-project.eu/2010/10/veritas-presented-at-
siamoc-congress/
Forsyth D., Arikan O., Ikemoto L., O’Brien J. and
Ramanan D., 2005. Computational studies of human
motion.Foundation & Trends in Computer Graphics &
Vision, V.1 No.2,3: 77–254.
Ivekovic S. and Trucco E., 2006. Human Body Pose
Estimation with PSO. IEEE Congress on Evolutionary
Computation CEC-2006, Canada. P.: 4399-4406.
Jaklic A., Leonardis A., Solina F., 2000. Segmentation and
Recovery of Superquadrics. Computational imaging
and vision 20, Kluwer, Dordrecht.
Hofmann M., Gavrila D.M., 2009. Multi-view 3D Human
Pose Estimation combining Single-frame Recovery,
Temporal Integration and Model Adaptation. In
CVPR: 2214-2221.
Kovesi P., 2008. RANSAC software in MATLAB.
www.csse.uwa.edu.au/~pk/research/matlabfns/.
Leonardis A., Jaklic A., Solina F., 1997. Superquadrics for
Segmenting and Modeling Range Data. In IEEE Conf.
Proc.. PAMI-19 (11). P. 1289-1295. DOI:
10.1109/34.632988.
Moeslund T., Hilton A. and Kruger V., 2006 A survey of
advances in vision-based human motion capture and
analysis. Computer Vision and Image Understanding,
104: 90–126.
Mun Wai Lee, Cohen I., 2004. Human Upper Body Pose
Estimation in Static Images. In ECCV (2): 126-138.
Shotton J., Fitzgibbon A., Cook M., Sharp T., Finocchio
M., Moore R., Kipman A., and Blake A. Real-Time
Human Pose Recognition in Parts from a Single Depth
Image. CVPR, IEEE, June 2011.
Sminchisescu C. and Triggs B., 2003. Estimating
articulated human motion with covariance scaled
sampling. Int. J. Robotics Research, 22(6): 371–393.
Solina F. and Bajcsy R., 1990. Recovery of parametric
models from range images: The case for superquadrics
with global deformations. IEEE Transactions PAMI-
12(2):131-147.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
302