
REAL TIME OBJECT TRACKING ON GPGPU
∗
Maciej Chociej and Adam Polak
Theoretical Computer Science Department, Faculty of Mathematics and Computer Science, Jagiellonian University,
Krak
´
ow, Poland
Keywords:
Motion Tracking, GPGPU, Optical Flow, Foreground Separation.
Abstract:
We propose a system for tracking objects in a video stream from a stationary camera. Our method, as of-
ten used, involves foreground-background separation and optical flow calculation. The major finding is fast
feedback process that leads to an accurate detection of background-object and object-object boundaries and
maintaining them during object occlusions. The contribution of this paper also includes improvements to com-
puting dense optical flow and foreground separation. The methods described were implemented on a GPGPU
and yield performance results sufficient for real time processing. Additionally, our approach makes no a priori
assumptions on the characteristics of tracked objects and can be utilized to track both rigid and deformable
objects of various shapes and sizes.
1 INTRODUCTION
Object tracking is one of central problems in com-
puter vision. Robust tracking algorithms need to com-
bine techniques from many areas of the field. Ques-
tions that need to be answered are:
• what are the objects we want to track;
• what are the cues that allow us to separate an ob-
ject of our interest from its surroundings;
• what abstractions to model an object with and how
to maintain their correspondence in time.
Even more questions arise when motion is taken into
account:
• how to detect movement accurately and fast in
terms of computation time;
• how should detection of movement influence the
way we partition objects in the image space;
• can we through motion analysis distinguish be-
tween objects that are involved in complicated,
dynamic interactions.
The literature on the subject is vast and presents many
methods that respond to most of these questions. In
a recent survey (Yilmazr et al., 2006) tracking algo-
rithms are divided based on the representation of the
∗
This paper is based on work funded by Polish Ministry
of Science and Higher Education (grant R00 0081 11) in
cooperation with AutoID Polska S.A.
objects as: a single point or points, simplified geo-
metric shapes, object contours and silhouettes and ar-
ticulated shape models constructed from the former
types. In (Bugeaue and P
´
erezz, 2008) the authors
reassign those algorithms to three distinct groups:
detect-before-track, track and combine partitions and
the third group: track distinct features or feature dis-
tributions. The first type of algorithms relies on ex-
ternal schemes that detect classes of well known ob-
jects (license plates (Donoser et al., 2007)(Zweng
and Kampel, 2009), vehicles (Feris et al., 2011), hu-
mans and human faces (Karlsson et al., 2008)(Wu and
Nevatia, 2007) and describe them in terms of simple
structures like points or bounding boxes, which then
can be tracked over time. The second type is based
on a primary detection of objects, possibly by exter-
nal means. Such objects silhouettes, usually repre-
sented by the contour or an energy function in the im-
age space, are then evolved to meet specific energy
preservation criteria. The last group consists of al-
gorithms focusing on the detection and tracking of
unique features in the appearance of the objects and
by their movement predicting and extrapolating the
movement of an object as a whole.
The paper (Bugeaue and P
´
erezz, 2008) contains
an interesting review of those three types of algo-
rithms, their strengths and drawbacks and proposes
a hybrid method combining those approaches. Our
method is based on similar premises, but varies sig-
nificantly in details. By exploiting the power of GPG-
303
Chociej M. and Polak A..
REAL TIME OBJECT TRACKING ON GPGPU.
DOI: 10.5220/0003862303030310
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 303-310
ISBN: 978-989-8565-04-4
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
PUs we compute dense optical flow that allows us
to predict object deformations with higher precision.
The quality of our optical flow also makes us less de-
pendent on detecting ’observations’ (in the sense of
(Bugeaue and P
´
erezz, 2008)), as object identification
can be propagated for much longer time. Finally in
(Bugeaue and P
´
erezz, 2008) object distinction is per-
formed via multiple graph-cuts, whereas we employ
a delayed voting scheme. In the scenario with a sta-
tionary camera this allows us to process high resolu-
tion inputs with real-time performance and compara-
ble accuracy.
It is worth to mention that there exist another ap-
proach to combine the three mentioned types of algo-
rithms, i.e. data fusion (Makris et al., 2011).
2 THE PROBLEM
In this paper we propose a method that can be used
to solve the following basic problem: In each frame
of a given video stream we want to separate moving
objects and assign to them unique identifiers. These
identifiers should be discovered as soon as the object
appears in the view and should be held as long as the
object is visible.
An additional goal is to strike a proper balance be-
tween the precision and the computational cost. We
strove for real-time performance and thus decided to
focus on algorithms where natural data parallelism in
the image space could be exploited.
Our method is intended to work at the lowest level
of a more complex tracking system. It is designed to
be easily integrated with higher level logic capable of
handling more difficult object-object interactions.
We define an object as a group of pixels forming
a connected component of the input image and mov-
ing in a coherent way. We do not make any other
assumptions about tracked objects. This makes our
method general and versatile, capable of tracking hu-
mans in motion, vehicles, as well as other moving ob-
jects, both rigid and deformable. However, we require
that the camera is stationary and that it is, without los-
ing generality, in an upright orientation.
When tracking the objects we face the following
major problems which need to be solved:
• detecting new objects, and separating them from
the background;
• resolving object occlusion;
• separating objects which move together in close
proximity in the same direction;
• splitting objects which we incorrectly tracked as a
single one;
• joining objects which we detected separately but
seem to be parts of one physical entity.
We have implemented our method on multicore CPUs
and CUDA based GPGPUs and performed extensive
tests that included footage from various indoor and
outdoor scenarios. These tests had shown that our
approach handles with reasonable accuracy all these
cases, apart from the last one – joining object parts.
We leave this to be solved with higher level logic,
which is the goal of our future work.
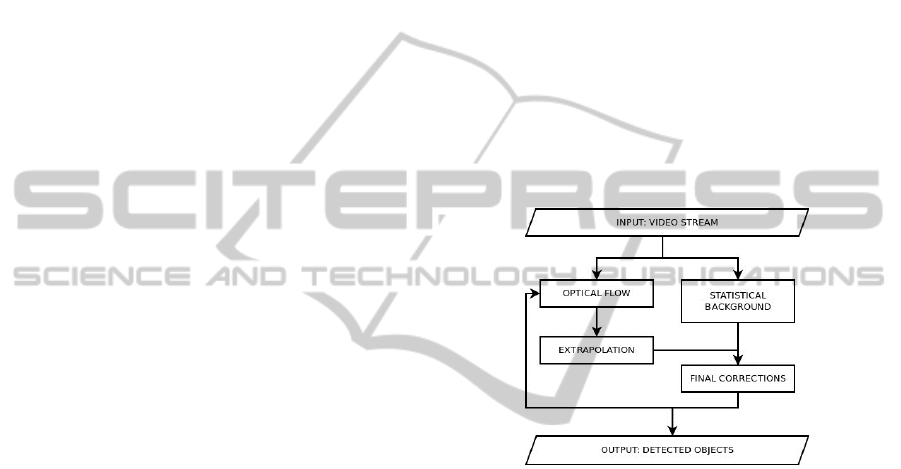
3 METHOD OVERVIEW
The main modules our method consists of are pre-
sented in the figure below. It is followed by the gen-
eral description of these modules.
Figure 1: Block diagram of our method.
Our procedure processes consecutive frames ap-
pearing in the video stream. After the frame is pro-
cessed we return its partition into a number of tracked
objects and the background.
When the new frame appears in the video stream,
we process it as follows:
1. Optical Flow. We compute the optical flow be-
tween the previous and the current frame. The
method we use exploits the object partition com-
puted for the previous frame.
2. Extrapolation. We predict the location of tracked
objects in the current frame using the computed
optical flow and the previous frame.
3. Statistical Background. We compute the
foreground-background separation in the current
frame based on statistical model of the back-
ground.
4. Final Corrections. We apply small corrections
to the extrapolated partition from the second step.
These include:
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
304

Figure 2: An example frame from the PETS 2006 dataset, left to right: the original frame, the optical flow, the extrapolation,
the foreground, the final object partition.
• splitting objects that are not coherent anymore;
• detecting new object that appeared for the first
time in the current frame;
• assigning IDs to pixels which are in the
foreground according to the foreground-
background separation but have no IDs
reasoned from the extrapolation phase.
The algorithms we devise to complete these steps are
described in details in the next section.
4 ALGORITHMS
4.1 Optical Flow
The optical flow pass we use is a block matching al-
gorithm organized in a coarse-to-fine way similar to
the well known Bouguet’s (Bouguet, 2000) imple-
mentation of the Lucas–Kanade window registration
scheme (Lucas and Kanade, 1981). This method had
been often discarded in application to dense optical
flow due to complications that arise when tracking ob-
jects with low texture or frequent occlusions. By care-
fully choosing appropriate features to track one can
limit the negative influence of the aperture problem,
but this in general results in sparse optical flow esti-
mation (Tomasi and Kanade, 1991)(Shi and Tomasi,
1993). Other methods incorporate many ways to in-
troduce a global constraint of smoothness (Horn and
Schunck, 1981). This solves the aperture problem but
on the other hand tends to distort information where
flow discontinuities appear. It is also computation-
ally more expensive as global constraints arise and
the solution cannot be tackled locally. State of the
art optical flow algorithms (Bruhn et al., 2005)(Xu
et al., 2010) exploit both these ideas with great ac-
curacy, but are prohibitively slow and do note seem
to fit for GPGPU architectures. In order to compute
dense optical flow with attention to fine object silhou-
ette tracking we introduced improvements to the pyra-
midal scheme of (Bouguet, 2000).
4.1.1 Basic Definitions
The optical flow algorithm processes the two consec-
utive images from the video stream L, C and an iden-
tifier map ID that contains the object partition of L.
The output consists of a matrix of size width × height
containing pairs: (u, v) ∈ Z
2
of displacements com-
puted for each pixel that belongs to an object.
In the first step two pyramids of image miniatures are
created for L and C. Let us denote these image minia-
tures by L
i
and C
i
(0 ≤ i ≤ l). Each of the l + 1 lev-
els is a matrix containing extended pixel touples, each
level half the width and half the height of the previ-
ous. We will refer to the level 0 as the top and to the
level l as the bottom. The extended pixel touples con-
tain three values representing the color components r,
g, b and two additional values h and v for the horizon-
tal and vertical gradient values. In order to downsize
the images we use a small Gaussian kernel. An aux-
iliary pyramid of identifiers, denoted ID
i
, is created
from the ID map. The selection of the pixel’s identi-
fier is performed by choosing the most frequent iden-
tifier from the four pixels directly above in the higher
pyramid level.
For the window registration algorithms we will use
a normalized dissimilarity measure, based on a
componentwise L
1
norm, that compares pixels’ r-
neighborhoods (for a given radius r).
d
IJ
(p
1
, p
2
) =
∑
v∈{−r,...,r}
2
kI[p
1
+ v] − J[p
2
+ v]k
(2r + 1)
2
(1)
4.1.2 Self-dissimilarity
The aperture problem arises most commonly from the
appearance of two types of regions in the analyzed
REAL TIME OBJECT TRACKING ON GPGPU
305

images: large spots with low or none texture (e.g.
solid blocks of one color) and regions with repeat-
ing self-similar patterns (e.g. a checkered fabric of
ones clothing). The dissimilarity between windows
on consecutive frames is low and near constant in the
local neighborhood or has multiple regular minimums
in those parts of the image. This leads to random op-
tical flow estimation when we minimize the dissimi-
larity in order to find the proper window registration.
To prevent such behavior we must first detect which
regions hold those unwanted properties. For a given
radius r we define a pixel’s self-dissimilarity as:
sd
I
(p) =
∑
v∈{−r,...,r}
2
d
II
(p, p + v) (2)
This quantity tells us weather a pixel’s local neighbor-
hood is similar to many such neighborhoods in near
proximity. High self-dissimilarity implies the pix-
els neighborhood is unique, low self-similarity hints
us that the pixels neighborhood might be mistaken
by a similar neighborhood nearby. Our experiments
have shown that in the areas of low self-dissimilarity
the standard unmodified optical flow algorithm often
finds illusionary movement where none has actually
happened, or detects no movement where there has
been some. The choice of using average dissimilarity
rather than minimum was based on experiments con-
ducted. The minimum of dissimilarities was much
more influenced by image noise and resulted in less
informative level sets.
For a given limit of dissimilarity lim we compute a
pyramid of matrices SD
i
matching the sizes of the im-
age and ID pyramids, that contains self-dissimilarity
information from the pyramid L
i
. We start at the bot-
tom and proceed to the top. The resulting level-0
self-dissimilarity map SD
0
describes the regions of
the image in terms of susceptibility to the aperture
problem. A level-0 pixel (i.e. SD
0
[x, y] = 0) has local
neighborhoods in every image in the image pyramid
at least lim dissimilar. Similarly: a level k pixel (i.e.
SD
0
[x, y] = k) has dissimilarity at least lim in the pyra-
mid levels l up to k.
4.1.3 Window Scaling and Object Masking
Our algorithm will utilize a registration windows of
different sizes. We incorporate the scaling factor c
into the dissimilarity measure d
IJ
:
d
IJ
(c, p
1
, p
2
) =
∑
v∈{−r,...,r}
2
kI[p
1
+ cv] − J[p
2
+ cv]k
(3)
Moreover, in order to improve the accuracy of the
window registration in regions with motion occlusion
we decided to incorporate an additional constraint to
Figure 3: The self-dissimilarity map: pixel values ranging
from 0 (blue) to 5 (red).
the dissimilarity measuring function. Optical flow
methods like (Sun et al., 2010) try to segment the im-
age based on coherency of optical flow, we use the ob-
ject assignment in a similar manner. For a given pixel,
we take into account only those pixels from it’s neigh-
borhood that belong to the same object. If a pixel has
an ID set (and only those are processed when com-
puting the optical flow) we consider only those pixels
from the r-neighborhood that share the same ID.
4.1.4 Coarse to Fine Window Registration
In the main part of our optical flow algorithm we
find the displacements with a dynamic window reg-
istration approach. Similar concept of adaptive win-
dow sizes and shapes has been mentioned in (Kanade
and Okutomi, 1994)(Yang et al., 2004). In the fol-
lowing we will use a new variable s which is to be
fixed afterwards due to some experiments. At each
level we limit ourselves to integer displacements can-
didates v ∈ {−1, 0, 1}
2
. With l + 1 pyramid levels this
results in maximal displacements of 2
l
in total. At
the bottom, for every pixel we choose s best displace-
ments that minimize the dissimilarity between the lo-
cal neighborhoods in the consecutive frames. At lev-
els l − 1 through 0 we utilize the s best candidates
from the level directly below as starting offsets for the
displacement vectors. We use the self-dissimilarity
map to scale the window when required. If process-
ing a pixel that has the self-dissimilarity level higher
than the currently processed pyramid level we need to
make the window larger.
For performance reasons we calculate the optical
flow only for the pixels where an object has been dis-
covered. Our experiments show that for the sake of
accuracy it is useful to rise the number of samples
that are compared when computing dissimilarity with
a bigger window. In most of our tests 6 levels of the
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
306

image pyramid were sufficient to detect the largest
displacements. Considering that a pixel at the bottom
level would represent a 32 × 32 pixel square at the
highest resolution, we increase the number of sam-
ples in the d
IJ
dissimilarity measure by a factor of 4
up to 16.
The nature of the other components in the tracker
allows us to limit the search to integer displacements.
Most differential optical flow algorithms find dis-
placements with sub-pixel precision. This often re-
quires bilinear interpolation as pixel values need to be
resolved at real coordinates. Our experiments have
shown that s = 3 not only compensates this lack of
precision in the lower levels, but in fact often gives
better results.
Figure 4: Behavior of optical flow algorithms on regions
with low texture: left – pyramidal LK, right – our method.
4.2 Extrapolation
The main task of this algorithm is to predict where
objects detected in the previous frame are going to ap-
pear in the current one. We do this in a rather straight-
forward manner. To extrapolate a location of an ob-
ject we process all pixels belonging to it and trans-
late them by vectors computed during the optical flow
phase. Apart from the object partition, from the pre-
vious frame we get the confidence value in each pixel.
During the extrapolation phase we will extrapolate
them as well, while the section 4.4 will elaborate in
detail on how these confidence values are initiated in
the first place. After some experiments we have de-
veloped two heuristics which improve the quality of
the extrapolation.
The optical flow computed using our method falls
victim to some irregularities and in each frame a frac-
tion of pixels is extrapolated in the wrong direction.
To prevent this, we check for each pixel whether it’s
optical flow vector is close enough to the average opti-
cal flow calculated in the pixel’s neighborhood. If this
condition fails we do not extrapolate the given pixel
at all.
Two pixels from the previous frame (possibly be-
longing to two different objects) can be extrapolated
to the same pixel in the current frame. It means that
one object occludes another and we need to decide
which of them is closer to the camera. In order to
resolve this we assume, without losing of generality,
that the camera is in an upright orientation. Thus we
assume that an object located lower in the image is
also closer. This method performs fine when object
movement is limited to a plane, or close to a plane.
Many surveillance scenarios allow such an assump-
tion. More complicated tracking cases, where the ob-
jects can move freely in all three dimensions, would
require a different method.
4.3 Statistical Background/Foreground
Detection
In order to reinforce the information coming from the
extrapolation phase we detect foreground objects by
analyzing statistical properties of the video stream.
The foreground detection module maintains a long
term model of the background that contains the color
value mean and standard deviation for each pixel.
Apart from the long term model we keep two short
term statistics (mean and standard deviation) that are
gathered over the span of a limited number of frames
(say, by 0.5 sec). The long term color statistics are
used to decide weather a pixel from a new frame
belongs to the foreground. The short term parame-
ters inform us about the volatility of the pixel, which
is used to determine the background learning speed.
Additionally, we forbid changes to the background
model in the regions where the extrapolation phase
has already predicted an object.
The short term parameters are updated componen-
twise, by means of a moving average, with a constant
rate every time a new frame appears. The rate is high
(i.e. 0.1) in order to accumulate information over a
short period. The long term parameters are updated
componentwise with a much lower learning rate (i.e.
0.01) that also depends on the volatility of the pixel
and the contents of ID
0
. If volatility is high or we see
that the region belongs to an object, the learning rate
drops significantly. If the short term parameters are
stable, we increase the long term learning rate.
In order to detect regions belonging to the fore-
ground the difference between the color values in the
frame and the background model is measured and
thresholded. The long term deviation is used to de-
termine the threshold levels. We also introduce a
constant additive and a constant multiplicative factors
that can be used to scale the deviation, and control the
background-foreground separation sensitivity.
4.4 Final Corrections
The purpose of this phase is to combine data we acq-
REAL TIME OBJECT TRACKING ON GPGPU
307

uired from the extrapolation phase and the
background-foreground separation and then uti-
lize it to introduce corrections in the predicted ID
0
map of the current frame.
The algorithm consists of three steps, which are
preceded by computing new foreground map. A pixel
is said to be in the foreground if it belongs to any ex-
trapolated object or the statistical foreground.
4.4.1 Splitting Objects
This step is performed to assure that every extrapo-
lated object is coherent.
First, we find the connected components of the
foreground map. Each foreground pixel is connected
to its four neighbors and the resulting graph is a sub-
graph of a 2D-grid.
Then, for each extrapolated object we decide
which component it belongs to and remove parts of
this object from the remaining. We rank candidate
components summing confidence values of pixels be-
longing to the intersection of this component and a
given object.
The parts of the object that lie outside of the high-
est ranked connected component are subtracted from
the object.
4.4.2 Detecting New Objects
In this step we detect objects that were not present on
the previous frame. These are objects that appeared in
the view at this moment or were tracked as a part of
another object and were detached from it in the previ-
ous step. If there exists a connected component that
has an empty intersection with all the extrapolated ob-
jects we assign a new unique identifier to all the pixels
inside and set their confidence value to 1.
4.4.3 Filling Gaps
We define a gap as a pixel which is believed to belong
to the foreground but has no identifier assigned. Usu-
ally, at this stage of processing there are still such pix-
els left. We assign them to an object with a procedure
that searches the ID
0
map in a breadth-first manner.
For every gap pixel (x, y) we check its eight neigh-
bors and find the most frequent ID among them. If
this ID appears at least three times, we assign it to
this gap pixel. Pixel’s new confidence is set to the dif-
ference between the average confidence of neighbors
with the chosen ID and the second best. If such differ-
ence turns out to be negative, we leave the gap pixel
unchanged.
This procedure is iterated until no gap pixel
changes its identification.
5 IMPLEMENTATION DETAILS
The methods described have been prototyped in C++
and tested on x86 CPUs. The algorithms have been
then ported to NVIDIA CUDA environment. We have
implemented the foreground separation, the optical
flow, extrapolation and code related to processing the
foreground connected components on the GPU. The
only part that relies on CPU computation is the gap
fixing phase that requires a breadth-first approach.
Although there are BFS algorithms on GPGPUs we
have not decided to implement them for simplicity
reasons. The overhead related to synchronizing GPU
and CPU execution, transferring partial data and run-
ning BFS on the CPU has no major influence on over-
all performance.
The foreground separation proved to be easily par-
allelized, as pixels could be processed independently.
The optical flow phase is the most time consuming
part of the algorithm, thus its efficient implementa-
tion was the biggest challenge. The problem was
memory bandwidth constrained and required careful
attention when reading and writing data. A number of
approaches has been developed in order to make co-
alesced memory accesses possible. The optical flow
code had a deeply nested structure that had to be prop-
erly unrolled for performance reasons. The perfor-
mance tuning of the optical flow required a good bal-
ance between the shared memory usage and the num-
ber of simultaneously working blocks.
6 RESULTS
The figures at the end present the object segmentation
produced from various test scenarios. The scenario
depicted in the first figure shows a group of 6 persons
involved in complicated occlusions. The dimensions
of the image are 800 × 600 running at 15 frames per
second. The scenarios from the two middle figures are
taken from the PETS 2006 workshop datasets. These
streams have PAL resolution (i.e. 720 × 576) and are
recorded at 25 frames per second. The last scenario
was recorded with a 960 × 640 frame size at 12.5
frames per second.
Our software run on a Tesla C2050 GPU reaches
sustained real-time performance in these scenarios.
The average frame processing time varies from 15 to
25 milliseconds. The performance is greatly depen-
dent on the optical flow phase and thus on the total
area of tracked objects.
We have also tested the optical flow alone on
frames in PAL resolution counting displacement vec-
tors in every pixel. The processing time of 200 mil-
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
308

Figure 5: 6-person occlusions.
Figure 6: PETS 2006 dataset S1, camera 3.
Figure 7: PETS 2006 dataset S1, camera 4.
Figure 8: Parking lot.
liseconds is the pessimistic case we might be facing.
The prototype of our algorithms has been imple-
mented as a pure CPU solution. In simpler scenarios
(i.e. the parking lot) it reached near real-time per-
formance when run on a multicore Intel Xeon X5650
processor.
REAL TIME OBJECT TRACKING ON GPGPU
309

7 FURTHER WORK
Our tracker is a low-level solution and in order to im-
prove the detection and tracking quality higher level
logic might be implemented. In particular such logic
could observe the objects in the context of a longer
period of time, maintaining its history.
Our future work will focus on following issues:
• When a tracked person hides behind an obstacle
and then reappears it is detected as a completely
new object.
• Large number of objects appearing simultane-
ously in the stream results in lower tracking qual-
ity and performance, especially in cases with
complicated occlusions. There is need for an al-
gorithm for deciding which of the tracked objects
can be ignored (e.g. tracking only humans or ve-
hicles).
• Some surveillance scenarios include monitored
zones covered by more than one camera. Combin-
ing data from multiple trackers can lead to better
results.
With the above issues resolved our tracker to-
gether with those high level components might be
considered as an important part of a robust surveil-
lance system.
ACKNOWLEDGEMENTS
The authors would like to thank the PETS workshops
organizers for publishing the datasets we extensively
used in our tests.
REFERENCES
Bouguet, J.-Y. (2000). Pyramidal implementation of the
lucas kanade feature tracker description of the algo-
rithm.
Bruhn, A., Weickert, J., and Schn
¨
orr, C. (2005). Lucas
kanade meets horn schunck: Combining local and
global optic flow methods. International Journal of
Computer Vision.
Bugeaue, A. and P
´
erezz, P. (2008). Track and cut: Simul-
taneous tracking and segmentation of multiple objects
with graph cuts. Journal on Image and Video Process-
ing.
Donoser, M., Arth, C., and Bischof, H. (2007). Detecting,
tracking and recognizing license plates. In Proceed-
ings of the 8th Asian conference on Computer vision -
Volume Part II, Berlin, Heidelberg. Springer-Verlag.
Feris, R., Siddiquie, B., Zhai, Y., Petterson, J., Brown,
L., and Pankanti, S. (2011). Attribute-based vehicle
search in crowded surveillance videos. In Proceedings
of the 1st ACM International Conference on Multime-
dia Retrieval, New York, NY, USA. ACM.
Horn, B. and Schunck, B. (1981). Determining optical flow.
Artifical Intelligence.
Kanade, T. and Okutomi, M. (1994). A stereo matching
algorithm with an adaptive window: Theory and ex-
periment. IEEE Trans. Pattern Anal. Mach. Intell.
Karlsson, S., Taj, M., and Cavallaro, A. (2008). Detection
and tracking of humans and faces. Journal on Image
and Video Processing.
Lucas, B. and Kanade, T. (1981). An iterative image regis-
tration technique with an application to stereo vision.
In Proceedings of the 7th International Joint Confer-
ence on Artificial Intelligence - Volume 2, San Fran-
cisco, CA, USA. Morgan Kaufmann Publishers Inc.
Makris, A., Kosmopoulos, D., Perantonis, S., and Theodor-
idis, S. (2011). A hierarchical feature fusion frame-
work for adaptive visual tracking. Image Vision Com-
put.
Shi, J. and Tomasi, C. (1993). Good features to track. Tech-
nical report, Cornell University, Ithaca, NY, USA.
Sun, D., Sudderth, E., and Black, M. J. (2010). Layered
image motion with explicit occlusions, temporal con-
sistency, and depth ordering.
Tomasi, C. and Kanade, T. (1991). Shape and motion from
image streams: a factorization method - part 3 detec-
tion and tracking of point features. Technical report,
Pittsburgh, PA, USA.
Wu, B. and Nevatia, R. (2007). Detection and tracking of
multiple, partially occluded humans by bayesian com-
bination of edgelet based part detectors. International
Journal of Computer Vision.
Xu, L., Jia, J., and Matsushita, Y. (2010). Motion detail pre-
serving optical flow estimation. In Computer Vision
and Pattern Recognition. IEEE Computer Society.
Yang, R., Pollefeys, M., and Li, S. (2004). Improved real-
time stereo on commodity graphics hardware. In Pro-
ceedings of the 2004 Conference on Computer Vision
and Pattern Recognition Workshop (CVPRW’04) Vol-
ume 3 - Volume 03, Washington, DC, USA. IEEE
Computer Society.
Yilmazr, A., Javed, O., and Shah, M. (2006). Object track-
ing: A survey. ACM Computing Survey, 38.
Zweng, A. and Kampel, M. (2009). High performance im-
plementation of license plate recognition in image se-
quences. In Proceedings of the 5th International Sym-
posium on Advances in Visual Computing: Part II,
Berlin, Heidelberg. Springer-Verlag.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
310
