OBJECT VOLUMETRIC ESTIMATION BASED ON GENERIC

FITTED PRIMITIVES FOR SERVICE ROBOTICS

Tiberiu T. Cociaș, Sorin M. Grigorescu and Florin Moldoveanu

Departament of Automation, Transilvania University of Brașov, Brașov, Romania

Keywords: Robot Vision, 3d Object Reconstruction, Surface Approximation, Primitive Fitting, Service Robotics.

Abstract: This paper present an approach for object surface estimation from a single perspective using a stereo camera

configuration. The goal of the method is to capture the particularity of an object of interest by fitting a

generic primitive who best models the recognized shape. The shape modeling process is performed on 3D

Regions of Interest (ROI) obtained by classifying the objects present in disparity maps. The principle uses a

number of control points, calculated from the primitive Point Distribution Model (PDM). These control

points drive the modeling behavior in the disparity point cloud data based on the principle of active

contours, or snakes. Finally a compact 3D object mesh can be generated using Delaunay triangulation. The

obtained PDM models are intended to be used for the purpose of precise object manipulation in service

robotics applications.

1 INTRODUCTION

Nowadays most service robotics applications use

depth perception for the purpose of environment

understanding. In order to precisely locate, grasp and

manipulate an object, a robot has to estimate as good

as possible the pose and the structure of that object

of interest. For this reason different visual

acquisition devices, such as stereo cameras, range

finder or structured light sensors, are used (Trucco

and Verri, 1998).

For online manipulation, together with the pose

of the object, it is needed to determine the 3D

particularities of the viewed structure in order to

estimate its shape (Hartley and Zisserman, 2004).

There are several types of methods that focus on

the 3D reconstruction of objects using multiple

perspectives. Such methods try to reconstruct the

convex hull of the object (Matsuyama et al., 2004),

or to recover its photo-hull (Kutulakos and Seitz,

2000). Other algorithms explore the minimization of

the object’s surface integral with a certain cost

function over the surface shape (Lhuillier and Quan,

2005).

On the other hand, the reconstruction can be

addressed also from a single view. This technique is

usually efficient when applied to regular surface

objects. An early approach for this challenge was

investigated for piecewise planar reconstructions of

paintings and photographs (Horry et al., 1997).

Subsequent improvements of the technique

(Criminisi et al., 2000), (Sturm and Maybank, 1999)

increased the geometric precision especially for

scenes with multiple vanishing planes.

In terms of reconstruction resolution and

accuracy, range images (e.g. from laser scanners)

provide one of the best surface estimations from all

techniques. However, it has speed deficiency, sensor

dimension and power consumption (Kim et al.,

2009).

The main challenge encountered during 3D

reconstruction is the automatic computation of the

3D transformations that align the range data. Thus,

the registration of different perspective point clouds

into one common coordinate system represents one

of the most researched topics in the vision

community (Kim, 2009), (Stamos et al., 2008).

The rest of the paper is organized as follows. In

Section 2 a brief description of the image processing

chain is provided. The main contribution of the

paper, that is the 3D shape modeling approach, is

given in Section 3. Finally, before conclusions,

performance evaluation results are presented in

Section 4.

191

CociaÈ

Z T., Grigorescu S. and Moldoveanu F..

OBJECT VOLUMETRIC ESTIMATION BASED ON GENERIC FITTED PRIMITIVES FOR SERVICE ROBOTICS.

DOI: 10.5220/0003862801910197

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 191-197

ISBN: 978-989-8565-04-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

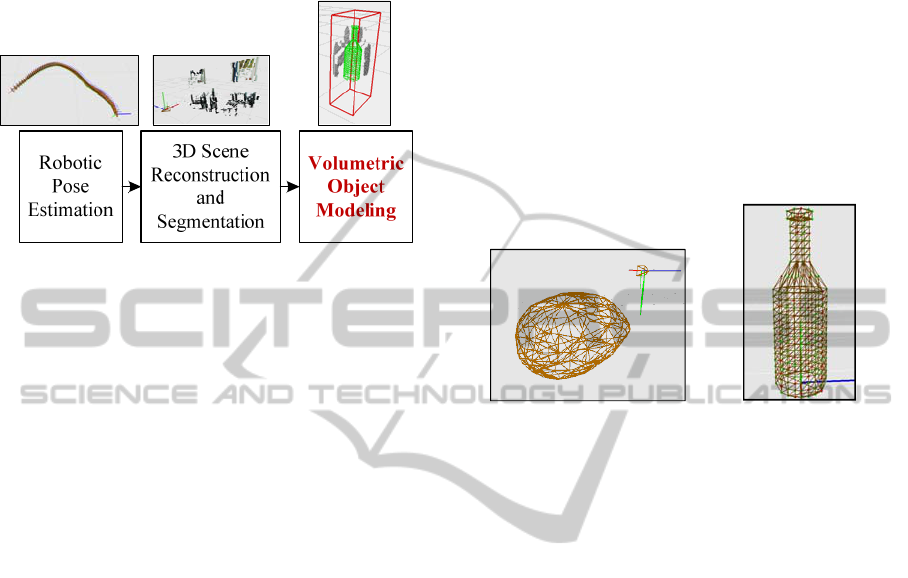
2 MACHINE VISION APARATUS

The block diagram of the proposed scene perception

system can be seen in figure 1.

Figure 1: Block diagram of the proposed scene perception

system.

The reference coordinates of the obtained visual

information is related to the on-line determined

position and orientation (pose) of a robot, that is, of

a robot’s stereo camera system (Grigorescu et al.,

2011). Once a certain pose is determined, the

imaged scene can be reconstructed and segmented

for the purpose of environment understanding. The

main objective here is to get the depth, or disparity,

map which describes the 3D structure of an imaged

scene. This information is further used by the final

object volumetric modeling algorithm, which is

actually the main focus of this paper. One of the

main algorithms used in the proposed vision system

is the object classification method which delivers to

the volumetric modeling method the object class and

the 2D object ROI. The classification procedure is

based on color and depth information. A detailed

description of the approach can be found in

(Grigorescu et al., 2011).

3 OBJECT VOLUMETRIC

MODELLING

The object volumetric modeling system is based on

the active contour principle used to manipulate a set

of pre-defined Point Distribution Models (PDM) by

stretching them over a disparity point cloud

describing an object in a given Region of Interest

(ROI). In the considered process, three main

challenges arise: the sparse nature of the disparity

maps, the calculation of the 3D ROI and the

nonlinear object modeling.

3.1 PDM Primitive

In the presented work, an object generic primitive is

defined as a PDM model which serves as a backbone

element forconstructing a particular object, or shape.

The generic PDM primitive is represented by a data

structure that has as background component a shape

vector  which contains 3D feature points

describing the model of an object class. Such

example models are shown in figure 2. Additionally,

the structure contains a scale factor , a rotation

matrix  and a translation matrix  that relates the

PDM to a canonical reference coordinate system.

(a)

(b)

Figure 2: Generic meshed PDM models. (a) Potato.

(b)Bottle.

Since in the considered source of visual

information, that is disparity images, only one

perspective of the imaged object is available, the

PDM model is actually used to compensate for the

missing information. In this case we consider objects

that have a symmetrical shape. Nevertheless, the

proposed approach can be applied on irregular

shaped entities. Depending on the complexity and

regularity of the surface object, the primitive model

can be defined either by a low or a high number of

3D feature points. For example, the bottle shown in

figure 2 is described by 382 feature points. Since the

PDM describing such an object represents a regular

surface, not all these points are important for the

object modeling process. The so-called control

points, namely those points that define the shape of

an object, can be automatically determined based on

three main characteristics (Cootes, 1995):

1. Points marking the center of a region or sharp

corners of a boundary;

2. Points marking a curvature extreme or the

highest point of an object;

3. Points situated at equal distance around a

boundary between two control points obeying

rule one.

In the same time, control points can be

determined manually under the guidance of a human

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

192

(Zheng et al., 2008). This last method captures the

features of an object more efficiently but suffers

from subjectivity on features definition since the

process is controlled by a human person. Depending

on the modeled object, in our approach we used both

the automatic and the manual techniques to

determine control points. Using the introduced

points, the computation time is increased since the

number of points describing the shape of an object is

usually much lower than the total number of points

from the PDM. The 3D positions of the PDM points

are actually directly dependent on the positions of

the control points, as it will later be shown in this

section. For example, from a total of 382 points

describing the bottle primitive from figure 2(b), only

71 of them (marked with red dots) are considered to

be control points. On the other hand,for a complex

object, this number can be equal to the initial PDM

features number, meaning that all points from the

primitive are considered to be control points since

all of them are needed to capture a specific feature.

Taking into account a lower number of control

points will considerably increase the computational

speed of the modeling process.

3.2 Disparity Map Enhancement

As opposed to newer structured light sensors, such

as the MS Kinect

, one main drawback of the

considered visual information is the sparse 3D

structure of disparity maps. Namely, it contains

“holes” or discontinuities in areas where no stereo

feature matching exists (Brown, 2003). Such

discontinuities are present in low textured regions or

constant color areas from the environment.

To overcome this issue we propose an

enhancement method which deals with disparity

maps discontinuities. Basically, the idea is to scan

each point from a disparity image and determine if

there is a gap between the considered point and a

neighboring point situated at a certain distance, as

shown in figure 3(a). Since we apply the principle

on disparity maps, which are defined on the 2D

domain, there are only 5 main neighboring

directions from a total of 8 in which we search for

discontinuities. The untreated 3 directions refer to

the back of the centered point and it is assumed that

are no discontinuities in that direction since the

position is already searched.

The disparity map is actually a grey scale image

with pixel intensities inverse-proportional to the

distance between the considered 3D world point and

the camera’s position. Having in mind that the

disparity image is represented using 8 bits, we

sample it using 256 layers, each corresponding to

certain intensity in the disparity domain. The

enhancement process searches for discontinuities

only in one layer at a time, since there is no

information about the connectivity of the intensities.

In this sense, the layers are stored using a 256 bins

histogram. For each pixel in each layer the number

of the same intensity along a direction is calculated.

In order not to merge two different objects, the

search area is reduced to a finite value, dynamically

calculated. The search process starts from the lowest

neighboring distance value, which has a two pixels

length, and ends when a discontinuity is found or the

maximum length is reached. The discontinuity is

determined by comparing the length of the direction

with the number of the same intensity pixels found

along this direction. If the number of pixels found is

below the length of the considered direction, the

missing positions are filled with pixels with the

same intensity as the ones alreadyfound.

(a)

(b)

(c)

Figure 3: Disparity enhancement algorithm. (a) Missing

pixels searching principle. (b)Original disparity map. (c)

Enhanced disparity image.

There is a slight chance that two closely

positioned objects are merged by the algorithm. In

order to overcome this challenge, a variance driven

image of the disparity map has been used (Turiac et

al., 2010). From the variance image only object

contours are extracted. In this way it can be

determined if the points which take part in the fill

process belong to one single region or to a

neighboring region. The result of the presented

method will be a compact and dense representation

of the disparity image, as shown in figure 3(c). On

the other hand, it is needed to connect the layers

OBJECT VOLUMETRIC ESTIMATION BASED ON GENERIC FITTED PRIMITIVES FOR SERVICE ROBOTICS

193

which are very close (in terms of disparity) in the 3D

model. This can be achieved by diffusing the

gradient separating two neighboring intensities. In

order to preserve the 3D features of the object, the

diffusing process will occur only for regions with

translation of intensity no grater then 5 intensities

layers. In this way, the obtained layers are smoothly

connected.

3.3 3D ROI Definition

The 2D segmentationand classification process

provides, besides the class to which the object

belongs, a ROI feature vector

],[

,  = 1,2,3,4

defined in the stereo image pair domain. This

description restricts the object search area to a

quadratic region of interest. By computing the

disparity between the left and right ROI points we

obtain a 3D representation of the considered ROI. In

this way only a planar representation (slice)in the 3D

space is obtained. The volumetric property is

evaluated starting with the assumption that the pixels

inside the 2D ROI describe only the object. The

depth is determined statistically by finding the

highest density of 3D points which lie inside the

planar ROI along the Z 3D Cartesian axis. A 3D

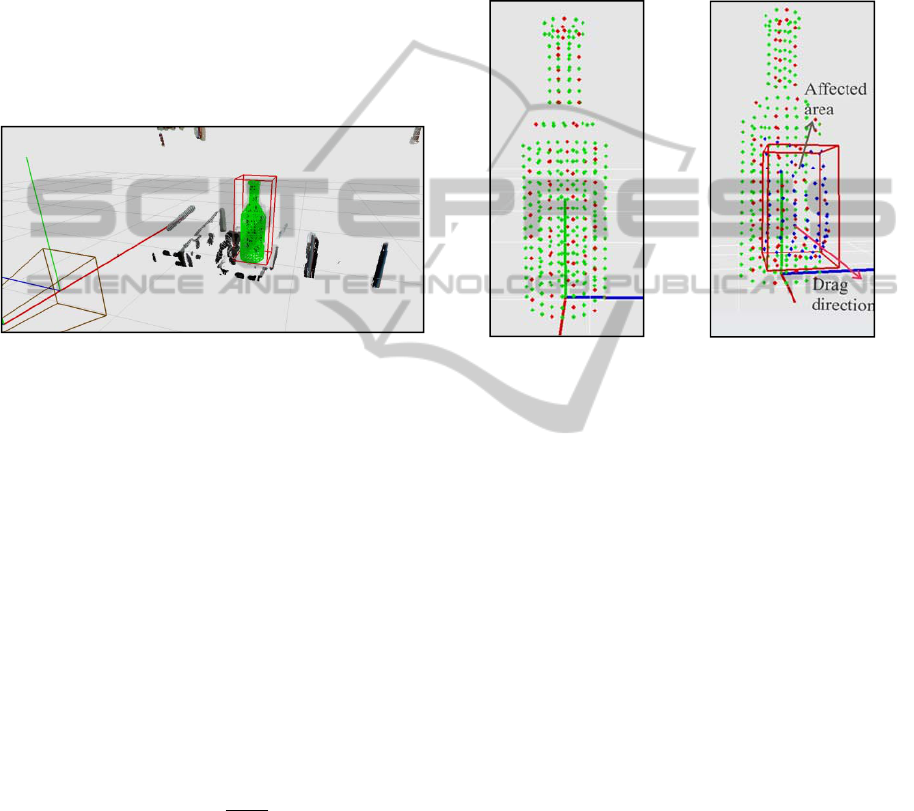
representation of the ROI can be seen in figure 4.

However, there is a possibility that the highest

density of 3D points belongs to a noise entity outside

the object border but still inside the ROI.

(a) (b)

Figure 4: 3D ROI computation. (a) Input image together

with the calculated 2D ROI. (b) 3D ROI reprojection.

To overcome this problem, a histogram of the

disparity image is calculated. Instead of searching

only the top density value of the intensities in

histogram, we check also the highest aperture of the

histogram for the considered top density. Basically

we determine the highest distribution of connected

points by summing all the densities from the slices

of the aperture belonging to a top value of the

histogram as:

∑

ihd ))(max(

(1)

Where d represent the highest cluster of 3D points,

ℎ() is the number of pixels for a certain bin i and a,

b are the closest and farthest non zero ℎ

(



)

relatively

to the considered intensity i, respectively. The

margin of the aperture is actually defining the first

and last planes of the 3D ROI volume along the Z

axis, respectively.

3.4 PDM Shape Alignment

The 3D alignment process deals with the calculation

of the rotation and translation of the primitive shape

with respect to the point cloud distribution of the

disparity information inside the 3D ROI. Because

each PDM, that is primitive and point cloud, is

defined in its own coordinates system, a similarity

transformationis used to align the two models. Since

the ROI’s PDM is related to the same coordinate

system as the 3D virtual environment, we have

chosen to bring the primitive’s PDM into a reference

3D environment coordinate system. The reference

coordinate system is given by the on-line determined

pose of the stereo camera (Grigorescu et al., 2011).

In this sense, the primitive is considered to be a

translational shape, while the 3D ROI is marked as a

static cube. The similarity transformation is

described by:





=(



−),

(2)

where,

old

X and

new

X represent the 3D coordinate

of a point before and after the similarity

transformation, s is a scale factor, while R and t are

the matrices defining the rotation and translation of a

point, respectively. These coefficients represent the

Degrees of Freedom (DoF) of a certain shape.

The scale factor is determined based on the 3D

point cloud information inside the ROI. Since a

disparity enhancement is considered before the 3D

reprojection process, it can be presumed that inside

the ROI exist one or more large densities of points

which describe the object of interest. Thus, by

evaluating the distribution of these densities we can

compute a percentage of the size difference between

the object PDM shape and the point cloud within the

3D ROI.

The translation of the moving shape is easily

determined by adding the center of gravity of the

points inside the 3D ROI from the center of gravity

of the primitive PDM, as follows:

∑∑

(3)

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

194

where,

represent the number of points of the

model and a and b are the two densities of points,

that is of the object’s shape (primitive model) and of

the fixed point cloud inside the 3D ROI. The

rotation matrix R is determined by evaluating the 3D

distribution of the disparity point cloud information,

that is, 3D slope from which the point data is

aligned.

By using the proposed alignment method, a

rough object volumetric estimation is obtained based

on the fitting primitive principle. An example result

of the similarity transformation can be seen in figure

5, where, the green silhouette represents the PDM

primitive shape.

Figure 5: Primitive PDM shape alignment example.

3.5 PDM Primitive Modeling

The points which drive the modeling process are the

control points described in a previous subsection.

The behaviorof the other points in the PDM model is

automatically derived from the movement of the

control points. The modeling process is achieved by

dragging after each control point the neighbors from

the surrounding area. Each of the neighbor point is

moved based on a physical relation describing the

property of the considered object. This relation can

be either linear, as in equation 4, or non-linear for

more complex surfaces. For simplicity if

explanations, we have considered in this work a

linear relation between control and the rest of the

PDM points:

max

⎟

⎠

⎞

⎜

⎝

⎛

curr

oldnew

(4)

where,

new

X and

old

X represent the new and old 3D

coordinates of the considered neighboring points,

respectively,

max

d is the distance between the

control point and the farthest neighbor within the

affected area and

curr

represent the distance

between the control point and the translated

neighbor. The results of such a linear modeling are

shown in figure 6, where control points are marked

with red, their neighbors are labeled with blue the

rest of the PDM points are green.The surrounding

dragged area has the shape of a cube centered on the

control point 3D coordinate and has its area defined

as double the distance between the initial and the

new position of the control point, as depicted in

figure 5.

(a) (b)

Figure 6: A linear dependency between a control point and

its neighbors. (a) Initial PDM shape model.(b) Point

deformation along a considered direction.

The proposed approach for estimating an object’s

volume starts with a generic object PDM model,

namely a primitive, and ends by capturing by each

primitive control point the local features of the

modeled object of interest. As explained, this is

achieved by minimizing the distance between the

control point and the PDM in a respective

neighborhood. The minimization procedure is based

on the active contours principle, better known as

snakes (Kass et al., 1988). This approach represents a

deformable contour model of the considered object.

In an image, an active contour is a curve

parameterized by the minimization of and energy

functional:

,))](())(([)()()(

intint

∫

+=ε+ε=ε dsscEscEccc

extext

(5)

where,

int

E and

ext

E are the internal and external

energies, respectively and () = [(), (), ()]

represents the curve describing the object’s surface.

while

]1,0[∈s

. By defining an initial contour within

an image, it will move under the influence of

OBJECT VOLUMETRIC ESTIMATION BASED ON GENERIC FITTED PRIMITIVES FOR SERVICE ROBOTICS

195

internal forces computed based on the derivatives

from the active contour an also under the influence

of the external forces captured from the image.

In the presented 3D object modeling approach,

the disparity image domain is equivalent to the 3D

representation of the scene. For this reason the same

energy minimization principle has been used to

model the shape of an object. Instead of using an

initial active contour, as in the original method, we

propose the use of a 3D generic primitive PDM

model. The movement of the contour surface is thus

described by the direction of the lowest functional

energy, that specific region actually corresponding

to aprobable contour in the image (Mark et al.,

2002). In the considered 3D case being the highest

density of points from the 3D scene.

The idea of using forces to move the primitive

points is that the primitive PDM must be attracted

and fitted on the border of the object. The internal

forces, which refer exclusively to the primitive

PDM, are responsible for supervising the shape

smoothness and continuity. As described in the

equation 6, the continuity property is controlled by

the first derivate while smoothens is define by the

second derivate of the surface.

),)()()()((

int

svssvsEEE

curvcont

β+α=+=

(6)

where,

cont

is the energy responsible for the

continuity of the surface and

curve

deals with the

bending property of the hull of the object.

and

are two parameters which influence the

cont

and

curve

E forces, while

)](),(),([)( szsysxsv =

represent

the coordinates of a point from the shape vector X.

In the discreet domain the two energies can be

rewritten as:

)()()(

−−−

−+−+−=

iiiiiicont

zzyyxxE

(7)

,)2(

)2()2(

+−

+−+−

+−+

+−++−=

iii

iiiiiicurv

zzz

yyyxxxE

(8)

where,

x ,

y ,

X∈

ni ...1=

and

is the

number of points in the shape PDM vector. In the

original formulation of the principle, each point

from the shape can be moved in one of the eight

possible 2D directions. In current3D approach,

because of the third dimension, a number of 24

directions are taken into account.

The correct moving direction is mainly

influenced by the external energy

ext

E which

evaluates for each direction the highest density of

3D points. Because this density can be spatially very

close, a weight factor for the external energy is

introduced. Thus, if these candidate positions have

an appropriate number of points, the weight factor

will be considered zero.

Since we have only one perspective of the

object, there are large object areas with no 3D point

cloud description needed to drive the contour

energies. The un-imaged back side of an object

represents such an example. In the proposed

approach, the missing information is filled by the

generic data introduced by the PDM primitive

model.

4 EXPERIMENTAL RESULTS

For evaluation purposes, a Point Grey Bumblebee

stereo camera system mounted on an autonomous

platform equipped with a robotic manipulator was

used. The objects used during tests were placed at

random location on flat surfaces present. The exact

location of an object is unknown. We tested the

algorithm on two different types of objects, namely

bottles and potatoes having different irregular

shapes. The bottles object class represents a large

number of geometrical regular shapes frequently

encountered in domestic settings. The potato is used

to test the algorithm against complex irregular

surfaces.

The Ground Truth (GT) data against which the

proposed method has been tested is composed of a

number of manual measurements conducted on the

objects: width, height, thickness, translation and

rotation. The translation and rotation was measure

with respect to a fixed reference coordinate system

represented by an ARToolKit

marker.

Table 1: Performance evaluation results for the proposed volumetric modelling system.

Shape Width[m] Height[m] Thickness[m] Φ[deg]

θ[deg] ϕ[deg]

[m] [m] [m]

Bottle

GT 0.085 0.35 0.08 0 1.3 5.7 0.1 0.05 0.850

Online 0.086 0.3491 0.0749 1.121 2.12 5.27 0.088 0.061 0.869

Potato

GT 0.087 0.059 0.06 0 2.5 1.5 0.1 0.05 0.850

Online 0.0855 0.0637 0.0651 2.08 1.67 -0.38 0.09 -0.055 0.873

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

196

Because of its regular shape, the volumetric

estimation of bottles had the lowest modeling error,

as can be seen from Table. 1. The modeled primitive

captured efficiently the particularity of the surfaces,

thus resulting in a precise surface estimation. On the

other hand, due to their irregular shape, a higher

estimation error has been determined for the

considered potatoes. An example of obtained test

results can be seen in Table 1, were

Φ, θ and ϕ are

Euler angles and x, y, and z are positions along the

three Cartesian axes, respectively.

5 CONCLUSIONS

In this paper, an object volumetric modeling

algorithm for objects of interest encountered in real

world service robotics environments has been

proposed. The goal of the approach is to determine

as precisely as possible the 3D particular surface

structure of different objects. The calculated 3D

model can be further used for the purpose of visually

guided object grasping. As future work the authors

consider the time computation enhancement of the

proposed procedure through parallel computational

devices (e.g. Graphic Processors), as well as the

application of the method to other computer vision

areas, such as 3D medical imaging.

ACKNOWLEDGEMENTS

This paper is supported by the Sectoral Operational

Program Human Resources Development (SOP

HRD), financed from the European Social Fund and

by the Romanian Government under the projects

POSDRU/107/1.5/S/ 76945 and POSDRU/

89/1.5/S/59323.

REFERENCES

Brown, M., Burschka, D., Hager, G. 2003. Advances in

Computational Stereo, IEEE Transaction on Pattern

Recognition and Machine Intelligence, 25(8):993–

1008.

Cootes, T., Taylor, C., Cooper, D., Graham, J. 1995.

Active Shape Models-Their Training and Application,

Comp. Vision and Image Understanding, 61(1):38-59.

Criminisi, A., Reid, I., Zisserman, A. 2000. Single View

Metrology, International Journal on Computer Vision,

40(2):123–148,

Grigorescu, S., Cocias, T., Macesanu, G., Puiu, D.,

Moldoveanu, F. 2011, Robust Camera Pose and Scene

Structure Analysis for Service Robotics, Robotics and

Autonomous Systems, 59(11):899-909.

Hartley,R., Zisserman, A. 2004. Multiple View

Geometryin Computer Vision, Cambridge University

Press.

Horry, Y.,Anjyo, K., Arai, K. 1997. Tour into the Picture:

Using a Spidery Mesh Interface to Make Animation

from a Single Image, Proc. ACM SIGGRAPH.

Kass, M., Witkin, A., Terzopoulos, D. 1998. Snakes:

Active Contour Models, International Journal of

Computer Vision, 1(4):321-331.

Kim, T., Seo, Y., Lee, S., Yang, Z., Chang, M. 2009

Simultaneous Registration of Multiple Views with

Markers,Computer-Aided Design, 41(4):231–239.

Kutulakos, K., Seitz, S. 2000. A Theory of Shape by

Space Carving, International Journal of Computer

Vision, 38(3):199–218.

Lhuillier, M., Quan, L. 2005. A Quasi-Dense Approach to

Surface Reconstruction from Uncalibrated Images,

IEEE TPAMI, 27(3):418–433.

Matsuyama, T., Wu, X., Takai, T., Wada, T. 2004. Real-

Time Dynamic 3-D Object Shape Reconstruction and

High-Fidelity Texture Mapping for 3-D Video, In

IEEE Transactions on Circuits and Systems for Video

Technology, 14(3), 357–369.

Stamos, I., Liu, L., Chao, C., Wolberg, G., Yu, G., Zokai,

S. 2008. Integrating Automated Range Registration

with Multi-view Geometry for the Photorealistic

Modeling of Large-Scale Scenes. International

Journal of Computer Vision, Springer, 78(2/3):237–

260.

Sturm, P., Maybank, S. 1999. A Method for Interactive 3D

Reconstruction of Piecewise Planar Objects from

Single Images, In BMVC.

Trucco, E., Verri, A. 1998.Introductory Techniques for 3-

D Computer Vision, Prentice Hall PTR.

Turiac, M., Ivanovici, M., Radulescu, T. 2010.Variance-

driven Active Contours, International Conference on

Image Processing, Computer Vision, and Pattern

Recognition.

Zheng, Y., Barbu, A., Georgescu, B., Scheuering, M., and

Comaniciu, D. 2008. Four-Chamber Heart Modeling

and Automatic Segmentation for 3D Cardiac CT

Volumes Using Marginal Space Learning and

Steerable Features,IEEE Transaction on Medical

Imaging, 27(11):1668–1681.

OBJECT VOLUMETRIC ESTIMATION BASED ON GENERIC FITTED PRIMITIVES FOR SERVICE ROBOTICS

197