
VISUALISING SMALL WORLD GRAPHS
Agglomerative Clustering of Small World Graphs around Nodes of Interest
Fintan McGee and John Dingliana
School of Computer Science and Statistics, Trinity College Dublin, Dublin, Ireland
Keywords:
Graph Visualisation, Graph Theory, Clustering Algorithms, Graph Display.
Abstract:
Many graphs which model real-world systems are characterised by a high edge density and the small world
properties of a low diameter and a high clustering coefficient. In the ”small world” class of graphs, the
connectivity of nodes follows a power-law distribution with some nodes of high degree acting as hubs. While
current layout algorithms are capable of displaying two dimensional node-link visualisations of large data sets,
the results for dense small world graphs can be aesthetically unpleasant and difficult to read, due to the high
level of clutter caused by graph edges. We propose an agglomerative clustering which allows the user to select
nodes of interest to form the basis of clusters, using a heuristic to determine which cluster each node belongs
to. We have tested three heuristics, based on existing graph metrics, on small world graphs of varying size and
density. Our results indicate that maximising the average cluster clustering coefficient produces clusters that
score well on modularity while consisting of a set of strongly related nodes. We also provide a comparison
between our clustering coefficient heuristic agglomerative approach and Newman and Girvan’s top-down Edge
Betweenness Centrality clustering algorithm.
1 INTRODUCTION
Many real-world networks across different fields have
similar characteristics and can be classified as small
world graphs (Watts and Strogatz, 1998). Small world
networks are characterised by two properties. The
first is the average of the shortest path between each
pair of vertices for the entire graph. The second prop-
erty is the average local clustering coefficient of the
graph, which is defined as the average of the clus-
tering coefficients for each vertex. Given an undi-
rected graph G = (V,E), where V is a set of vertices
{v
1
,v
2
...v
n
} and E is a set of edges e ∈ E connect-
ing vertices x ∈ V and y ∈ V with e(x,y) = e(y, x), the
neighbourhood of a vertex v, denoted Γ
v
is defined
as the set of all vertices adjacent to v, not including
v itself. The clustering coefficient for a vertex , de-
noted by γ
v
is most commonly defined as the ratio
of edges connecting the neighbours of a vertex to the
maximum number of edges that could possibly con-
nect the neighbours of the vertex (Watts, 2003). The
clustering coefficient c for a vertex v in an undirected
graph is given by
γ
v
=
|E(Γ
v
)|
k
v
2
(1)
where |E(Γ
v
)| is the magnitude of the set of edges
connecting neighbours of the vertex, k is the neigh-
bourhood size of the vertex, i.e.|Γ
v
|and
k
v
2
is the
maximum possible number of edges in Γ
v
. From
the above it can be seen that a vertex needs at least
two neighbours to have a valid clustering coefficient
value. To determine if a graph can be considered a
small world graph, it is compared to a randomly gen-
erated graph with the same number of vertices and
edges. A small world graph has approximately the
same average path length, but a considerably higher
(by orders of magnitude) clustering coefficient.
1.1 Motivation
Our motivation is to make graphs more comprehen-
sible. We are focusing on small world graphs specif-
ically due to the presence of groups of highly con-
nected nodes and the strong likelihood of clusters
within the graph as well as the common occurrence
of small world properties in real world networks. If
a user has nodes of specific interest to them, reorgan-
ising the layout of the graph based on the nodes of
interest may aid in their analysis. For example a user
may want to view a graph describing a large program
focusing on specific classes. The purpose of our clus-
678
McGee F. and Dingliana J..
VISUALISING SMALL WORLD GRAPHS - Agglomerative Clustering of Small World Graphs around Nodes of Interest.
DOI: 10.5220/0003864306780689
In Proceedings of the International Conference on Computer Graphics Theory and Applications (IVAPP-2012), pages 678-689
ISBN: 978-989-8565-02-0
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: A small world graph based on the connection be-
tween a small set of Wikipedia articles (|V | = 91|E| = 418)
laid out using a simple force directed algorithm.
tering approach is to aid in the layout by clustering
nodes around the user’s nodes of interest. The cluster-
ing assigns nodes in such a way that they are clustered
around nodes that they are more conceptually related
to. If grouping a node with one node set over another
results in a higher heuristic score for that clusters, we
can infer that the node conceptually belongs more to
that set. In less dense graphs a clustering may be obvi-
ous as there will be few links between clusters. How-
ever for more dense graphs useful clusterings may not
be so obvious and the density of edges can make the
graph more difficult to read. The purpose of this pa-
per is to determine what heuristic is best suited for our
approach to clustering.
1.1.1 Edge Density
The links in a node link visualisation convey impor-
tant information. However if they become too dense
the graph becomes less comprehensible, resulting in
nodes and other links becoming obscured. In terms of
graph theory the density of a graph is usually consid-
ered the ratio of edges to the maximum possible num-
ber of edges in the graph (Coleman and Mor, 1983).
For an undirected graph this can be described as
d =
|E|
|(V |(|V | − 1)/2)
(2)
A graph is then considered dense in theoretical terms
if this ratio approaches 1.0. However in practical
real world examples of information visualisation such
dense graphs are rarely seen. If we consider the
density of a graph to be the ratio of edges to nodes
d
l
= |E|/|V |, often referred to as the linear density,
most real graphs have a value of d
l
<= 10 (Melan-
con, 2006), however this is still enough to cause a
large amount of clutter. Melacon et al. give an exam-
ple of real world graphs which have even higher den-
sities, such as webcrawl graphs with d
l
= 25.57. The
Figure 2: The graph from figure 1 clustered using our ap-
proach around the four most well connected nodes, us-
ing clustering coefficient as a clustering heuristic, and
bundling(Holten, 2006) of inter-cluster edges.
graph in figure 1 has a density value d
l
= 4.59, which,
while not the most dense example, still appears diffi-
cult to read due to the number of edges. It is clear that
graph theoretic density scales the number of edges
more dramatically for a change in vertex count, so for
comparison of densities between graphs with different
node counts linear density provides a clearer result.
However for understanding the impact of density on
graphs with a constant node count, the graph theoretic
density is clearer as it does scale evenly between the
maximum and minimum edge count. Purchase (Pur-
chase, 1997) has demonstrated how the crossing of
edges is the graph aesthetic which affects most hu-
man understanding of the graph. Unfortunately in
large dense graphs edge crossings are unavoidable.
We hope that by clustering the graph intelligently,
strongly related nodes will appear closer to each other
within the same cluster. This will reduce long edges
and the likelihood of edge crossings.
2 RELATED WORK
2.1 Small World Graphs
Milgram (Milgram, 1967) first described small world
graphs in his work focused on social networks. The
concept was more recently revived by (Watts and
Strogatz, 1998) and has been shown to hold true for a
variety of networks, such as the relationships between
actors and films (Auber et al., 2003) as well as com-
puter systems (Cai-Feng, 2009), models of biological
networks(Watts and Strogatz, 1998) and citation net-
works (van Ham, 2004).
VISUALISING SMALL WORLD GRAPHS - Agglomerative Clustering of Small World Graphs around Nodes of Interest
679

2.2 Clustering
(Eades and Feng, 1997) describe clustered graphs as
graphs with recursive clustering structure over the
vertices. In their example the clustering structure is
an attribute of the graphs and vertices. However in
many cases, if a graph is to be clustered, there may
be no intrinsic attribute or parameter which describes
the clustering hierarchy. There are many different ap-
proaches to generating an optimum clustering as it
is a difficult problem that is NP-complete (Newman
and Girvan, 2004). Approaches to graph clustering
can be considered geometric or non-geometric. The
aim of geometric clustering is to have vertices that
are geometrically close to each other share a cluster
and vertices that are distant from each other appear
in separate clusters. An example of such a cluster-
ing is given by Quigley and Eades’ FADE algorithm
(Quigley and Eades, 2001) in which a quad-tree is
used alongside a modified force directed algorithm.
There are many different methods of non-geometric
clustering. Some methods such as Markov Cluster-
ing (MCL) (Van Dongen, 2000) and spectral portion-
ing (Frishman and Tal, 2007) use an algebraic ap-
proach, working on a mathematical representation of
the graph. Other methods such as Edge Betweenness
Centrality Clustering (Newman and Girvan, 2004)
use a graph based approach, calculating properties of
vertices or edges that are then used to partition the
graph into clusters. Quigley and Eades’ geometric
approach can be considered a bottom up (agglomer-
ative) approach while Newman and Girvan’s is con-
sidered top-down (divisive) approach. An agglomera-
tive clustering algorithm merges set of nodes together
to form clusters, a divisive approach divides the full
set of nodes into clusters. Schaeffer (Schaeffer, 2007)
provides an in depth review of clustering methods and
methods for evaluating cluster quality.
2.2.1 Clustering Evaluation
Newman and Girvan (Newman and Girvan, 2004) de-
fine a measure of the quality of a division of a net-
work graph, referred to as modularity. The measure
is used to evaluate their community detection algo-
rithm (which is essentially a top-down clustering al-
gorithm). The measure has also been used in work
by Newman (Newman, 2004) as a heuristic value for
building clusters. This metric is based upon the num-
ber of edges that start and end in the same cluster (re-
ferred to as communities in Newman and Girvan’s pa-
per). Auber et al (Auber et al., 2003) and Chiricota et
al. (Chiricota et al., 2003) use a quality measure de-
veloped by (Mancoridis et al., 1998) and utilised in
their clustering tool ”Bunch”. This measure, denoted
MQ (Modularisation Quantity) computes a value for
any given partition of a graph. Chiricota et al. and
Auber et al. use a slightly modified version of MQ
that is defined only for undirected graphs as an eval-
uation measure. The MQ value is used by the Bunch
tool as a function to be optimised to provide a good
clustering, rather than as a metric to evaluate one.
Boutin and Hascoet (Boutin and Hascoet, 2004) dis-
cuss many clustering evaluation approaches (referred
to by them as clustering validation indices) and they
note that these evaluations are often difficult to inter-
pret and compare.
Difference between Modularity and Modularisa-
tion Quantity. The MQ metric differs to Newman
and Girvan’s modularity measure. The latter com-
pares the fraction of all edges that are intra-cluster
edges to the fraction of all edges that are inter-cluster
edges. The former is a measure of the difference be-
tween the average ratio of actual intra-cluster edges
to the maximum amount of intra-cluster edges possi-
ble and the average ratio of the amount of inter-cluster
edges to the maximum amount of inter-cluster edges
possible. This means that modularity depends purely
on the number of edges, which is bounded to the num-
ber of nodes. MQ depends on the number of edges
and the number of nodes directly, as the maximum
possible number of edges between two clusters is a
function of the number of vertices.
3 PROPOSED APPROACH
Our approach consists of an agglomerative clustering
algorithm, focused on nodes of interest selected by
the user. We grow the clusters around each of these
nodes of interest by adding nodes based on a heuristic
evaluation of the quality of the resulting clustering of
the graph.
3.1 Chosen Heuristics
Modularity. Per Newman and Girvan (Newman
and Girvan, 2004) the modularity, Q, is calculated as
Q =
∑
i
(e
i
i −a
2
i
) (3)
Where e
i
i is the fraction of all edges that start and
end in cluster i and a
i
is the fraction of all edges that
terminate in cluster i. A modularity score of 1.0 indi-
cates that all edges are intra-cluster edges, a score of
0.0 indicates the clustering is equivalent to a random
one. Newman (Newman, 2004) uses modularity as a
guiding heuristic for a greedy agglomerative cluster-
ing process.
IVAPP 2012 - International Conference on Information Visualization Theory and Applications
680

Modularisation Quantity (MQ). We calculate MQ
using Auber et al’s approach (Auber et al., 2003) for
undirected graphs. Let A and B be two sets of disjoint
nodes in a graph G = (V,E) , let s equal the ratio of
edges between the two sets to the maximum possible
number of edges between the two sets.
s(A,B) =
|E(A,B)|
|A| ·|B|
(4)
Note that this ratio can be calculated for a set with
itself. For a cluster A in an undirected Graph without
self linking edges
s(A,A) =
2(|E(A,A)|)
|A| ·(|A| − 1)
(5)
If cluster A is a clique s(A,A) = 1. A clique is a set of
nodes where every node is connected to every other
node in the set. If none of the nodes in A are con-
nected s(A,A) = 0. If a cluster contains only a sin-
gle node, we define the s-value for that cluster to be
0. Given a partition ( also referred to as a clustering)
C = (C
1
,C
2
,....,C
p
) that divides the graph G = (V,E)
into p partitions the MQ score for that partition is
given by:
MQ(C;G) =
∑
p
i=1
s(C
i
,C
i
)
p
−
∑
p−1
i=1
∑
p
j=i+1
s(C
i
,C
j
)
p(p −1)/2
(6)
Essentially this is a measure of the difference be-
tween the s ratio of intra-cluster edges (denoted by
s(C
i
,C
i
) and the s ratio of inter-cluster edges (denoted
by s(C
i
,C
j
).
Clustering Coefficient. The clustering coefficient
of a graph is described in section 1. When we cal-
culate the average clustering coefficient of a cluster,
we only consider the nodes and their neighbours from
within that cluster. The average clustering coefficient
of a cluster describes how well inter-connected the
cluster is. This implies that the higher the cluster-
ing coefficient of a cluster the more strongly related
the nodes within the cluster are. Unlike the previous
two metrics, this metric only applies to a single cluster
and not to all of the clusters so far defined within the
graph. Therefore a high average of the average clus-
tering coefficient for each cluster does not imply that
all clusters have a high average clustering coefficient.
A large standard deviation between the average clus-
tering coefficients of the clusters indicates that some
clusters have been created with a low quality of clus-
tering. In the cases where a clustering using a heuris-
tic other than clustering coefficient produces clusters
containing only one or two nodes, it is not possible to
calculate the average clustering coefficient of the clus-
ter so we assign the cluster a clustering coefficient of
-1.0. This results in a suitably decreased score that re-
flects to poor quality of the clustering, when rating the
graph using the average cluster clustering coefficient.
Random Assignment. In order to provide a com-
parison clustering in which no heuristic is used, we
have also implemented a random assignment of nodes
to clusters. A node is chosen at random from the
combined neighbourhood of the clusters and then ran-
domly assigned to one of the clusters that it is con-
nected to. The process is then repeated until all nodes
are assigned. Nodes can only be assigned to clusters
in which they have a neighbour, to allow a reasonable
comparison with the preceding heuristics.
3.2 Initial Cluster Set Up
The initial set of nodes that are to form the basis of
the clustering is selected by the user. We term these
nodes supernodes. If our heuristic is either modularity
or MQ, or we are using the random approach, we can
begin to add further nodes to the clusters once the ini-
tial cluster nodes have been specified. This is because
it is possible to calculate modularity and MQ heuris-
tic value, or randomly choose a node, if a cluster con-
tains only 1 node. However this is not the case for the
clustering coefficient heuristic, as we need to have at
least two nodes existing already in the cluster before
we can calculate a valid heuristic value for a new node
being added. Therefore, before we start adding candi-
date nodes to the cluster using clustering coefficient as
a heuristic we need to add a second node to the cluster
of each of the supernodes. The nodes that are consid-
ered to be added are nodes within the neighbourhood
of the supernode. We would like to add a node that is
similar as possible to each of the supernodes, so we
use the Jaccard index of the supernode and the can-
didate second node’s respective neighbourhoods. The
Jaccard index of two sets of nodes A and B, ρ is de-
fined as:
ρ(A,B) =
|A| ∩|B|
|A| ∪|B|
(7)
If the super-node is denoted by v and the candidate
node is denoted by u we can write the Jaccard index
as
ρ(Γ(v),Γ(u)) =
Γ(v) ∩Γ(u)
Γ(v) ∪Γ(u)
(8)
The node which is used as the secondary node of
the cluster based around v is the node u for which
ρ(Γ(v),Γ(u)) is the largest. Ideally we aim to se-
lect a node where the neighbourhood Jaccard index
is 1. If the node chosen has already been assigned as
a neighbour of one of the other supernodes, we as-
sign the node to the supernode which results in the
VISUALISING SMALL WORLD GRAPHS - Agglomerative Clustering of Small World Graphs around Nodes of Interest
681

Figure 3: An example considering whether the green node
should be clustered with either the red or blue clusters us-
ing the clustering coefficient heuristic. The green node is
added to the blue cluster increasing the cluster’s local av-
erage clustering coefficient to 0.48. Adding it to the red
cluster would reduce its average local clustering coefficient
to 0.33.
best Jaccard neighbourhood index. The supernode
with the lower resulting Jaccard index is assigned the
node with the next highest resulting Jaccard index. If
this replacement node has also been assigned, we re-
peat the revaluation until all supernodes have been as-
signed distinct neighbours.
3.3 Assignment of Nodes to Clusters
Once the initial clusters are created, we store the
neighbourhood of each cluster and use this as input set
of nodes which can be potentially added to a cluster.
Given a clustering of p clusters C = (C
1
,C
2
,....,C
p
)
where each element of C contains a disjoint subset
of the graph G = (V,E) such that C
i
= v
1
,v
2
,...v
n
,
n = |C
i
| and C
i
⊂ V , we define the neighbourhood of
a cluster i as
Γ(C
i
) = (Γ
G
(v
1
) ∪Γ
G
(v
2
)... ∪Γ
G
(v
n
)) (9)
Each of the candidate nodes is added temporarily to
a cluster and a score based on that addition is calcu-
lated. The node which maximises the heuristic score
of the graph (or of each cluster) is permanently added
to the cluster. Once a node is added the process is
repeated until all nodes have been assigned to clus-
ters. The modularity and MQ heuristics are scored
for the graph as a whole, so once a node is added all
scores will have to be recalculated in the next round
of assignments. If the clustering coefficient heuristic
is being used, only the cluster average clustering coef-
ficient of the cluster which has had a node added will
have changed. The average clustering coefficients
calculated for the other clusters and their candidate
nodes will be unchanged from previous rounds. This
allows caching of the results for later reuse, therefore
it decreases computation time.
4 EVALUATION
4.1 Evaluation Graphs
We use Watts and Strogatz’s beta approach for cre-
ating small world graphs (Watts and Strogatz, 1998)
for evaluating the effectiveness of the heuristics. This
approach allows us to create a large set of graphs
of various densities and various levels of structure,
from regular lattices, to small worlds graphs, to com-
pletely random graphs. The approach begins by cre-
ating a lattice like structure with edges uniformly dis-
tributed across vertices, k edges per-vertex resulting
in |E| = k|V |. Each edge is rewired to a random target
vertex with a probability P. For a low value of P the
resulting graph is well structured and exhibits small
world properties. As P approaches 1 the graph be-
comes more like a randomly connected graph. Each
graph in our test set consists of 200 vertices. We have
generated graphs varying the input probability to the
beta model from 0.5 to 0.95. We have also varied
the Edge density of the graph from a graph theoretic
value of value of d = 0.015 to d = 0.3 , resulting in the
most dense graph having 11,940 edges. This is equiv-
alent to a range of linear edge densities from d
l
= 1.49
to d
l
= 29.85. We have clustered each graph using
our described heuristics. For evaluating the graphs
we also rate them using the MQ score and modular-
ity score of the resulting clustered graph, as well as
examining the average of per cluster average cluster-
ing coefficients and the standard deviation of the per
cluster average clustering coefficient. The four nodes
with the largest neighbourhoods have been selected as
the nodes of interest, resulting in four clusters. Due to
the random nature of the graph generation we have
averaged each result across 3 graphs generated with
the same input parameters. Our full test set of data
consist of 285 graphs for each of the three generation
runs. We display the results of the clustering for a
sample of the low density graphs in figure 4, a sample
of the high density graphs in figure 5, a sample of the
more structured graphs in figure 6 and a sample of the
more random graphs in figure 7. The standard devia-
tion of the heuristics across the 3 graphs is displayed
as the error bounds.
4.2 Results and Analysis
The effectiveness of each heuristic differs depending
on the density of the graph, how random the graph
is as a result of the input probability p of the gener-
ation algorithm, and the metric used for evaluation.
There are some constants however. Throughout the
graphs displayed in figures 4 through 7 it can be seen
IVAPP 2012 - International Conference on Information Visualization Theory and Applications
682
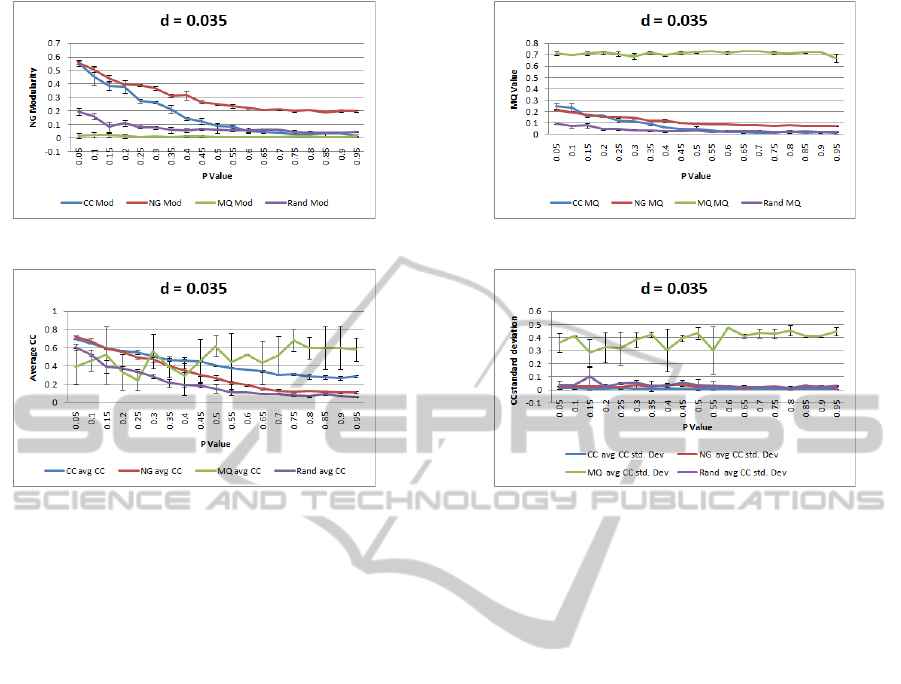
(a) Resulting graph modularity for each heuristic. (b) Resulting graph MQ score for each heuristic.
(c) Resulting average cluster clustering coefficient
for each heuristic.
(d) The standard deviation of the average cluster
clustering coefficient of each of the four clusters
for each heuristic.
Figure 4: Evaluation of graphs with 200 Nodes and a density of 0.035 (d
l
= 3.483), and an increasing level of randomness,
denoted by p value.
that the random approach of assignment of nodes to
clusters generally scores close to zero when evaluated
using modularity or MQ. This is to be expected as
both of these metrics lie in the range [−1,1] with zero
being equivalent to a random clustering. In the less
dense graphs sometimes the random approach does
score slightly above zero for a low input probability p,
when the graphs are less random. This is because of
the fact that our random approach does rely on nodes
to be connected to the clusters they are added to, re-
ducing the number of options for less well connected
nodes. For higher density graphs this is not evident
as a node will have a larger set of clusters it can be
assigned to. It is clear from each of these figures that
a graph scores well when it is rated with a metric that
is also used as the heuristic to build the clusters. It
also seems surprising that using MQ as a heuristic
results in a high average per cluster clustering coef-
ficient, however looking at the standard deviation of
the per cluster clustering coefficients shows that the
individual clusters vary wildly in quality. This is a re-
sult of a very imbalanced clustering, which will not be
of benefit to a user if the majority of nodes are placed
in a cluster with a low average clustering coefficient.
This means that the nodes within the cluster will be
less strongly related to each other.
4.2.1 Low Density Graphs
Figure 4 shows the resulting modularity, MQ and
clustering coefficient values when the algorithm is run
on graphs of increasing randomness with a relatively
low density, d = 0.035,d
l
= 3.483. Due to the rela-
tively low density, there are fewer nodes to be chosen
from when adding new nodes to the clusters, so nodes
being added to a cluster are more likely to closely re-
late to several of the other nodes within the cluster.
This is reflected by the higher scores for the random
layout approach for each heuristic for a low levels of
rewiring probability, see figure 4. Rating the graph
based on modularity (figure 4a) results in the best
results for the modularity heuristic with the cluster-
ing coefficient approach not far behind. The MQ ap-
proach noticeably scores similarly to the random ap-
proach. Rating the graph based on MQ (figure 4b)
results in a consistently high score regardless of the
level of randomness when using MQ as a heuristic.
Using the average cluster clustering coefficient as a
heuristic results in a low score of 0.2 for the more
structured graphs, but this diminishes toward 0.0 as
the graph becomes more random, making it no more
effective than the random approach. The modularity
heuristic scores similarly to the clustering coefficient
VISUALISING SMALL WORLD GRAPHS - Agglomerative Clustering of Small World Graphs around Nodes of Interest
683

(a) Resulting graph modularity for each heuristic. (b) Resulting graph MQ score for each heuristic.
(c) Resulting Average Cluster clustering coeffi-
cient for each heuristic.
(d) The standard deviation of the average cluster
clustering coefficient of each of the four clusters
for each heuristic.
Figure 5: Evaluation of a graphs with 200 Nodes and a density of 0.255 (d
l
= 25.3725), and an increasing level of randomness,
denoted by p value.
heuristic, for structured graphs and also diminishes,
but to a lesser degree than the clustering coefficient
approach. Rating the graph using average cluster
clustering coefficient (figure 4c), we can see that clus-
tering coefficient and modularity perform similarly
for structured graphs and diverge as the graphs be-
come more random. We can also see from the error
bounds that the MQ heuristic produces varying re-
sults for each of the 3 input graphs, where the other
approaches are consistent in their results. Even with
the large error bounds, once the graph becomes suf-
ficiently random, MQ appears to provide the highest
average clustering coefficient of the resulting clusters,
but if we look at the standard deviation of the average
clustering coefficient of each of the clusters created
by the MQ heuristic (figure 4d), we can see that the
quality of the clustering is quite poor. A large stan-
dard deviation of the average of the clustering coeffi-
cients of the 4 clusters indicates that while some clus-
ters have a high clustering coefficient others will have
a very poor one. This means the MQ does not in fact
provide a good consistent average cluster clustering
coefficient, therefore clusters will be created where
adjacent nodes do not have many mutual neighbours,
and will be less conceptually alike.
Conclusions: For graphs of low density clustering
coefficient and modularity are the preferred heuristics
when the graph contains structure. As the graphs be-
come more random modularity becomes the sole pre-
ferred heuristic.
4.2.2 High Density Graphs
Changing the density of the graph has an impact on
the performance of each of the heuristics. Figure
5 show results for graphs with a high density, d =
0.255,d
l
= 25.3725199. Rating the graphs based on
modularity (figure 5a), we see that overall the scores
are lower when compared to the less dense graphs,
however the same trends hold true as for the lower
density graphs. Rating the graphs based on MQ score
(figure 5b), we again see the MQ heuristic perform
well. A noticeable difference is the improved perfor-
mance of the clustering coefficient heuristic for the
more structured graphs. The modularity metric per-
forms better relative to clustering coefficient as graphs
become more random, but the scores are less con-
sistent, with larger standard deviations. Rating the
graphs based on average cluster clustering coefficient
results in the clustering coefficient heuristic perform-
ing the best for the more structure graphs. As the
graphs become more random, the MQ heuristic per-
IVAPP 2012 - International Conference on Information Visualization Theory and Applications
684

(a) Resulting graph modularity for each heuristic. (b) Resulting graph MQ score for each heuristic.
(c) Resulting average cluster clustering coefficient
for each heuristic.
(d) The standard deviation of the average cluster
clustering coefficient of each of the four clusters
for each heuristic.
Figure 6: Evaluation of a graph with 200 Nodes and a constant input rewiring probability p = 0.1, and an increasing density.
formance does appear to perform slightly better, but
the larger standard deviation in results across the in-
put graphs reveals it does not do so. Also, as for the
less dense graphs, the standard deviation of the av-
erage clustering coefficient (figure 5d) of each clus-
ter is much higher than the clustering coefficient ap-
proach. It is noticeable that for most of the graphs the
modularity heuristic performs even worse than using
the random approach and that the clusters generated
vary largely in average clustering coefficient. Conclu-
sions: Clustering Coefficient is the most consistently
high performing heuristic across all metrics. Modu-
larity results in a large deviation in the average clus-
tering coefficient of individual clusters within a graph
as long as there is some structure in it. As the graph
approaches random, modularity performs similarly to
clustering coefficient, but there is not enough differ-
ence to recommend it above clustering coefficient.
4.2.3 Low Randomness Graphs
These are the graphs which exhibit small world prop-
erties. Rating the graphs based on modularity (fig-
ure 6a), we see the modularity heuristic score best as
expected, however the score decreases as the graphs
become more dense. The average clustering coeffi-
cient scores best out of the other heuristics and also
decreases similarly to the modularity approach as the
graphs become more dense. Using MQ as a heuris-
tic, modularity behaves erratically, with large error
bars and scores worse than random for the less dense
graphs, and similar to random for the more dense
graphs, with a large standard deviation. Rating the
graphs based on MQ (figure 6b), we see the expected
high score for MQ. Interestingly we see low scores
for modularity for both the less dense and most dense
graphs, however for graphs in the mid range of densi-
ties it does improve considerably, just about outper-
forming the clustering coefficient approach. Look-
ing at the average cluster clustering coefficient (figure
6c), we see clustering coefficient performs the best
at all densities, with close competition from modu-
larity at lower graph densities. The average cluster
clustering coefficient rating for the MQ heuristic still
exhibits a large standard deviation between individual
clusters (6b) for all densities. For more dense graphs,
the use of modularity as a heuristic performs quite
poorly.
Conclusions: The clustering coefficient heuristic
performs relatively well across all levels of density
for all metrics. The closest rival is modularity, which
is similarly effective until a density of approximately
0.19 (d
l
= 18.905) is reached.
VISUALISING SMALL WORLD GRAPHS - Agglomerative Clustering of Small World Graphs around Nodes of Interest
685
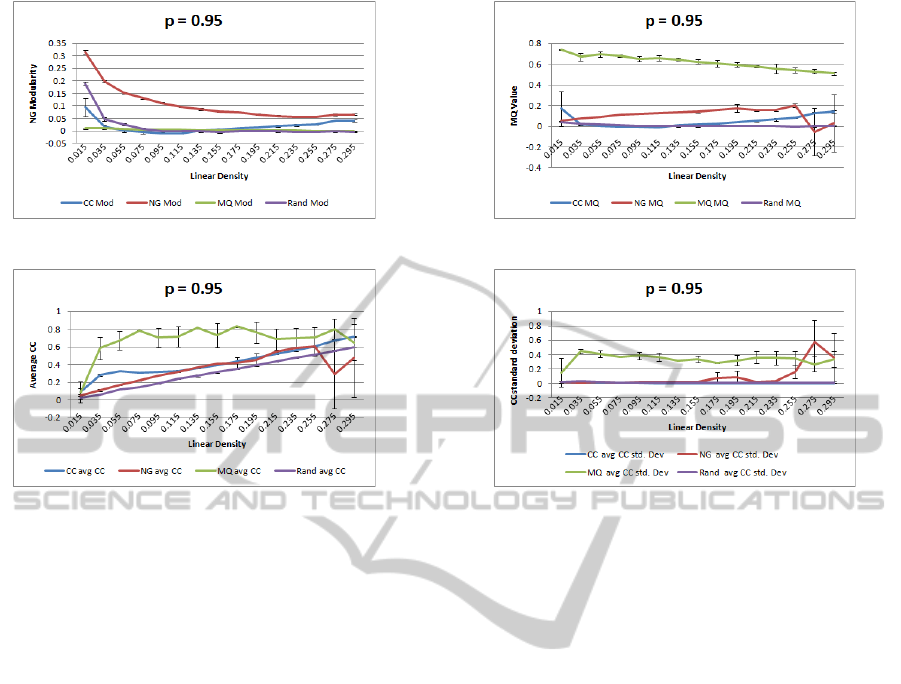
(a) Resulting graph modularity for each heuristic. (b) Resulting graph MQ score for each heuristic.
(c) Resulting average cluster clustering coefficient
for each heuristic.
(d) The standard deviation of the average cluster
clustering coefficient of each of the four clusters
for each heuristic.
Figure 7: Evaluation of a graph with 200 Nodes and a constant input rewiring probability p = 0.95, and an increasing density.
4.2.4 High Randomness Graphs
These are the graphs which exhibit a high level of ran-
domness, and thus exhibit no small world properties.
These graphs can give us insight into what approaches
are affected most by the absence of a high cluster-
ing coefficient. All heuristics other than modularity
perform poorly when rated using graph modularity
(figure 7a). Rating the graph using MQ (figure 7b),
we see, as expected, MQ performs very well, with
modularity performing poorly but better than random
or the clustering coefficient heuristic. When we rate
the graphs using average cluster clustering coefficient
(figure 9c) we see that there are some small improve-
ments over random using modularity and clustering
coefficients as heuristics, and that as graph density in-
creases the scores for these approaches increases in a
manner similar to the random approach. This is to be
expected given the random nature of the graph. From
this figure and figure 5b, we can see that when using
MQ as a heuristic and rating the final clustered graph
using MQ, the results are not reliable as they appear to
be independent of graph randomness and only slightly
affected by graph density.
Conclusions: Overall the best heuristic for graphs
which are more random and less structured appears
to be modularity, until the graphs become very dense
d = 0.26,(d
l
= 25.87), when average clustering coef-
ficient becomes marginally better.
4.2.5 Comparison with Edge Betweenness
Centrality Clustering
To provide a comparison with a state of the art cluster-
ing approach we performed a similar analysis on our
test data set having applied Edge Betweenness Cen-
trality clustering (Newman and Girvan, 2004). This
is a top town clustering approach which tries to find
naturally occurring clusters within the data. Unlike
our approach, the number of clusters is not usually
specified and there is no equivalent of a user specify-
ing nodes of interest. However it is an effective algo-
rithm which can distinguish the clusters which natu-
rally occur within a small world graph. The algorithm
generates a hierarchy of partitions. The partitioning
with the best modularity score is chosen from this hi-
erarchy as the final clustering. This can result in a
high number of clusters depending on the density and
structure of the graph, as can be seen in figure 10. In
many cases a very large number of clusters are cre-
ated, thus for our comparison we are constraining the
number of clusters formed by the Newman and Gir-
van approach to 4, the same number used for our ag-
glomerative clustering analysis. Evaluation uses the
same approach as that used for evaluating our cluster-
ing heuristics and the results can be seen in figures 8
IVAPP 2012 - International Conference on Information Visualization Theory and Applications
686
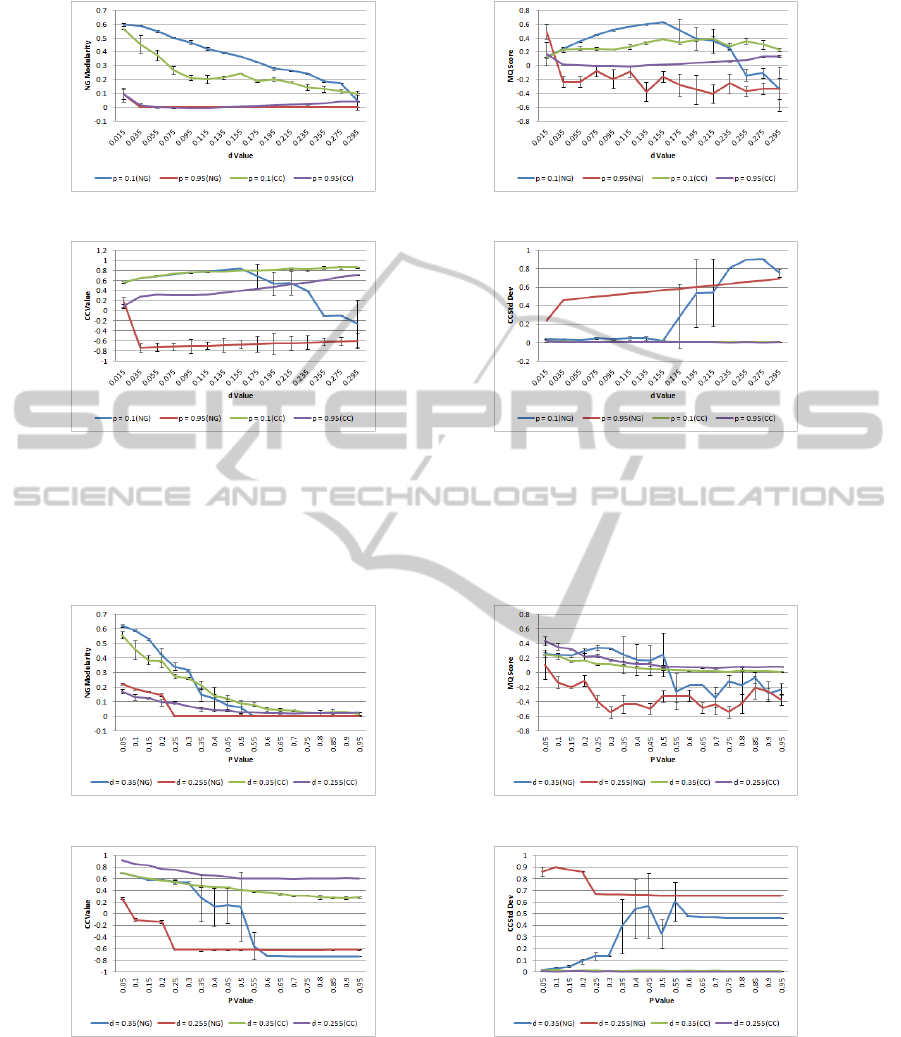
(a) Graph Modularity. (b) Graph MQ score.
(c) Average cluster Clustering Coefficient
of the 4 clusters.
(d) The standard deviation of the average
cluster Clustering Coefficient of each of
the clusters.
Figure 8: Evaluation of test graphs when clustered using Newman and Girvan’s Edge Betweenness Centrality clustering (NG)
and our clustering coefficient heuristic (CC) for comparison. The graphs display the metrics for well structured (p = 0.1) and
unstructured graphs (p = 0.95) of increasing density, where the number of clusters is constrained to 4.
(a) Graph Modularity. (b) Graph MQ score.
(c) Average cluster Clustering Coefficient
of the 4 clusters.
(d) The standard deviation of the aver-
age cluster clustering coefficient of each
of the clusters for high and low density
graphs, both with and without a predeter-
mined number of clusters.
Figure 9: Evaluation of test graphs when clustered using Newman and Girvan’s Edge Betweenness Centrality Clustering
(NG) and our clustering coefficient heuristic (CC) for comparison. The graphs display the metrics for low density (d = 0.035)
and high density graphs (d = 0.255) with an decreasing level of structure (p increasing), where the number of clusters is
constrained to 4.
VISUALISING SMALL WORLD GRAPHS - Agglomerative Clustering of Small World Graphs around Nodes of Interest
687
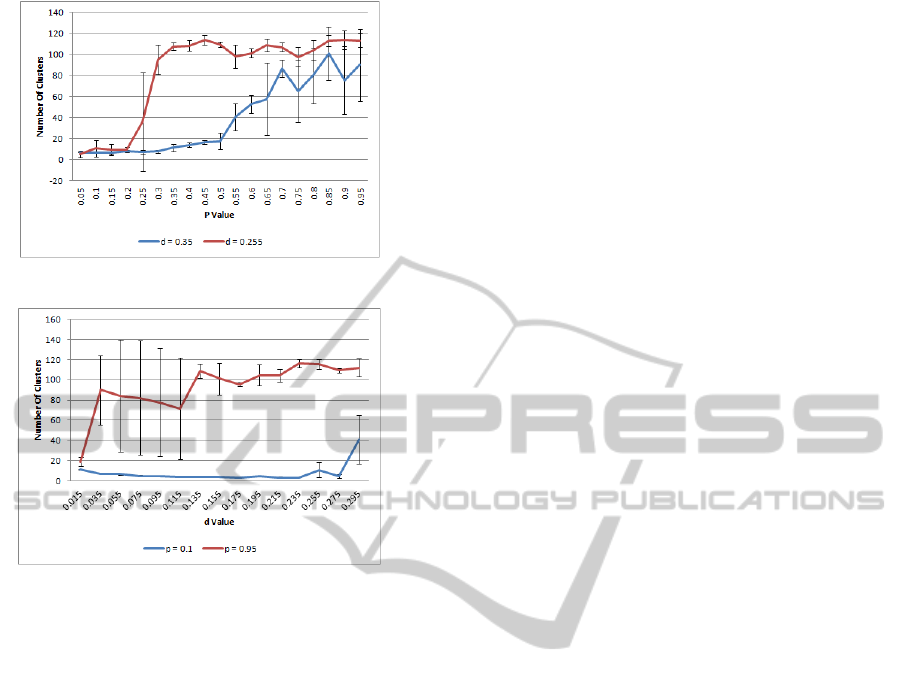
(a) Graphs with a constant density.
(b) Graphs with a constant rewiring probability.
Figure 10: Number of clusters generated using Edge be-
tweenness Centrality Clustering.
and 9.
Less Dense Graphs. When clustering lower density
graphs, compared to cluster coefficient heuristic ag-
glomerative approach, the cluster count limited ver-
sion of Edge Betweenness Centrality lustering pre-
dictably scores higher on modularity (figure 9a). This
is as the clustering is not constrained by the user spec-
ifying supernodes to form the basis of clusters and
the algorithm is very effective at finding the small
amount of clusters in the more structured graphs (see
figure 10). Predictably as the graph becomes more
random this difference diminishes until the cluster co-
efficient approach produces cluster with a higher level
of modularity, as there are fewer naturally occurring
communities for more random graphs. For the MQ
score, (see figures 9b , 8b) Edge Betweenness Cen-
trality clustering is superior, however the difference is
not as large, and once the graphs become less struc-
tured the performance of the approach drops off sig-
nificantly. In terms of clustering coefficient Edge Be-
tweenness Centrality clustering performs similarly for
the more structured graphs but drops off significantly
as the graphs become more random.
More Dense Graphs. From figure 8 it can be seen
that graphs with stronger small world graph character-
istics modularity is slightly better, but the clustering
coefficient approach performs better once the graphs
become slightly more random (at approximately p =
0.2, so the underlying structure is still quite strong).
However for the MQ score we find that, for the more
dense graphs, the clustering coefficient consistently
outperforms the Edge Betweenness Centrality clus-
tering approach. Our approach also provides equiva-
lent and better average clustering coefficient for clus-
ters and far higher clustering coefficient values for
the more random graphs (due to all of the singleton
clusters). Our approach also maintains more consis-
tently high clustering coefficient values for the more
dense graphs (d > 0.235, d
l
> 23.38) than Newman
and Girvan’s approach. The low standard deviation
between the clustering coefficients also indicates that
the resulting average clustering coefficient is balanced
across multiple clusters.
5 CONCLUSIONS AND FUTURE
WORK
Based on the preceding analysis the most consis-
tently effective heuristic for agglomerative clustering
around nodes of interest is clustering coefficient, es-
pecially for small world graphs. It scores well on
modularity and produces clusters with a high average
clustering coefficient that is balanced across all clus-
ters. The MQ scores for all heuristics other than MQ
are generally quite low, but average clustering coef-
ficient does perform well for dense graphs and with
a high level of structure. The clustering coefficient
heuristic was also was more stable when run over dif-
ferent graphs generated with the same input parame-
ters, as evidenced by the smaller error bars on the pre-
ceding graphs. Modularity also works as an effective
heuristic for agglomerative clustering, and is more ef-
fective than clustering coefficient when the graphs be-
come more random. However for small world graphs
clustering coefficient produces more consistent re-
sults in terms of the average clustering coefficient of
resulting graphs. MQ performed the least success-
fully of the heuristics when used for agglomerative
clustering. We also compared our agglomerative ap-
proach using clustering coefficient as a heuristic to
Newman and Girvan’s Edge Betweenness Centrality
algorithm, constrained to produce four clusters. The
comparison is not a direct one as the agglomerative
algorithm focuses on building clusters around nodes
of interest and the betweenness centrality algorithm
defines clusters without any such constraints. As ex-
IVAPP 2012 - International Conference on Information Visualization Theory and Applications
688

pected the Edge Betweenness Centrality clustering al-
gorithm performs very well on structured graphs with
low density. However as the graphs become more
dense the agglomerative algorithm performs close to
the level of the centrality algorithm and by some met-
rics (MQ and clustering coefficient) it outperforms the
algorithm for graph with a density of d = 0.255, d
l
=
25.373. Given that the agglomerative approach is de-
signed to focus around nodes of interest to aid in vi-
sualisation rather than discover communities, we feel
our algorithm compares favourably with the Edge Be-
tweenness Centrality algorithm.
This paper has examined the effectiveness of the
clustering heuristics purely using calculated metrics.
Further evaluation is required using user experiments
to determine fully the effect of the clustering on graph
comprehensibility. Such an evaluation could also
be extended to cover examples of real-world graphs,
rather than large sets of procedurally created ones.
Further work is required concerning the layout of
these clusters and their visualisation. Currently when
visualising the graphs we use a simple force directed
layout of individual clusters, however a graph layout
with consideration given to inter-cluster edges to re-
duce edge crossing could be very beneficial. Node
hierarchies are frequently used to aid layout, so one
potential application of the above clustering approach
is to recursive apply it to generated cluster to generate
a hierarchy to aid in layout and in the routing of edges
within large graphs. The routing of edges between
and within clusters also impacts graph comprehensi-
bility, so an approach such as Holten’s hierarchical
edge bundling (Holten, 2006) may be useful here.
REFERENCES
Auber, D., Chiricota, Y., Jourdan, F., and Melancon, G.
(2003). Multiscale visualization of small world net-
works. In Information Visualization, 2003. INFOVIS
2003. IEEE Symposium on, pages 75–81.
Boutin, F. and Hascoet, M. (2004). Cluster validity in-
dices for graph partitioning. In Information Visuali-
sation, 2004. IV 2004. Proceedings. Eighth Interna-
tional Conference on, pages 376 – 381.
Cai-Feng, D. (2009). High clustering coefficient of com-
puter networks. In Information Engineering, 2009.
ICIE ’09. WASE International Conference on, vol-
ume 1, pages 371–374.
Chiricota, Y., Jourdan, F., and Melancon, G. (2003). Soft-
ware components capture using graph clustering. In
Program Comprehension, 2003. 11th IEEE Interna-
tional Workshop on, pages 217 – 226.
Coleman, T. F. and Mor, J. J. (1983). Estimation of sparse
jacobian matrices and graph coloring problems. SIAM
Journal on Numerical Analysis, 20(1):pp. 187–209.
Eades, P. and Feng, Q.-W. (1997). Multilevel visualization
of clustered graphs. In Graph Drawing, pages 101–
112. Springer-Verlag.
Frishman, Y. and Tal, A. (2007). Multi-level graph lay-
out on the gpu. Visualization and Computer Graphics,
IEEE Transactions on, 13(6):1310–1319.
Holten, D. (2006). Hierarchical edge bundles: Visualization
of adjacency relations in hierarchical data. Visualiza-
tion and Computer Graphics, IEEE Transactions on,
12(5):741 –748.
Mancoridis, S., Mitchell, B., Rorres, C., Chen, Y., and
Gansner, E. (1998). Using automatic clustering to pro-
duce high-level system organizations of source code.
In Program Comprehension, 1998. IWPC ’98. Pro-
ceedings., 6th International Workshop on, pages 45
–52.
Melancon, G. (2006). Just how dense are dense graphs in
the real world?: a methodological note. In Proceed-
ings of the 2006 AVI workshop on BEyond time and
errors: novel evaluation methods for information vi-
sualization, BELIV ’06, pages 1–7, New York, NY,
USA. ACM.
Milgram, S. (1967). The small world problem. Psychology
Today, 2:60–67.
Newman, M. E. J. (2004). Fast algorithm for detect-
ing community structure in networks. Phys. Rev. E,
69(6):066133.
Newman, M. E. J. and Girvan, M. (2004). Finding and eval-
uating community structure in networks. Physical Re-
view E, 69(2):026113. Copyright (C) 2009 The Amer-
ican Physical Society Please report any problems to
prola@aps.org PRE.
Purchase, H. C. (1997). Which aesthetic has the greatest
effect on human understanding? In Proceedings of the
5th International Symposium on Graph Drawing, GD
’97, pages 248–261, London, UK. Springer-Verlag.
Quigley, A. and Eades, P. (2001). Fade: Graph drawing,
clustering, and visual abstraction. In Graph Drawing,
pages 77–80. Springer-Verlag.
Schaeffer, S. E. (2007). Graph clustering. Computer Sci-
ence Review, 1(1):27 – 64.
Van Dongen, S. M. (2000). Graph Clustering by Flow
Simulation. PhD thesis, University of Utrecht, The
Netherlands.
Van Ham, F. (2004). Case study: Visualizing visualization.
In Information Visualization, 2004. INFOVIS 2004.
IEEE Symposium on, pages r5–r5.
Watts, D. (2003). Small worlds: the dynamics of networks
between order and randomness. Princeton studies in
complexity. Princeton University Press.
Watts, D. and Strogatz, S. (1998). Collective dynamics of
”small-world” networks. Nature, 393:440–442.
VISUALISING SMALL WORLD GRAPHS - Agglomerative Clustering of Small World Graphs around Nodes of Interest
689
