ON STOCHASTIC TREE DISTANCES AND THEIR TRAINING VIA

EXPECTATION-MAXIMISATION

Martin Emms

School of Computer Science and Statistics, Trinity College, Dublin, Ireland

mtemms@tcd.ie

Keywords:

Tree-distance, Expecation-Maximisation.

Abstract:

Continuing a line of work initiated in (Boyer et al., 2007), the generalisation of stochastic string distance to

a stochastic tree distance is considered. We point out some hitherto overlooked necessary modiﬁcations to

the Zhang/Shasha tree-distance algorithm for all-paths and viterbi variants of this stochastic tree distance. A

strategy towards an EM cost-adaptation algorithm for the all-paths distance which was suggested by (Boyer

et al., 2007) is shown to overlook necessary ancestry preservation constraints, and an alternative EM cost-

adaptation algorithm for the Viterbi variant is proposed. Experiments are reported on in which a distance-

weighted kNN categorisation algorithm is applied to a corpus of categorised tree structures. We show that a

67.7% base-line using standard unit-costs can be improved to 72.5% by the EM cost adaptation algorithm.

1 INTRODUCTION

The classiﬁcation of tree structures into cate-

gories is necessary in many settings. In natu-

ral language processing an example is furnished by

Question-Answering systems, which frequently have

a Question-Categorisation sub-component, whose

purpose is to assign the question to one of a number of

predeﬁned semantic categories (section 5 gives some

details). Often one would like to obtain such a clas-

siﬁer by a data-driven machine-learning approach,

rather than by hand-crafting one. The distance-

based approach to such a classiﬁer is to have a pre-

categorised example set and to compute a category

for a test item based on its distances to examples in

the example set, such as via k-NN.

With items to be categorised represented as trees,

a crucial component in such a classifer is the mea-

sure used to compare trees. The tree-distance ﬁrst

proposed by (Tai, 1979) is a well motivated candidate

measure (see later for further details). This measure

can be seen as composing a relation between trees out

of several kinds of atomic operations (match, swap,

delete, insert) the costs of which are dependent on the

labels of the nodes involved. The performance of such

a distance-based classiﬁer is therefore very dependent

on the settings of these atomic costs.

In the work presented below probabilistic variants

of the standard tree-distance are considered and then

Expectation-Maximisation techniques are considered

as potential means to adapt atomic costs given a cor-

pus of training tree pairs.

Section 2 recalls the standard deﬁnitions of string-

and tree-distance. Section 3 goes on to ﬁrst recall the

stochastic string-distance as proposed by (Ristad and

Yianilos, 1998) and then deﬁnes stochastic variants of

tree-distance, which we term All-scripts and Viterbi-

script stochastic Tai distances D

(S,T) and D

(S,T).

The standard algorithm of (Zhang and Shasha, 1989)

for the tree-distance is then recalled and some nec-

essary modiﬁcations to allow correct and efﬁcient

computation of the All-scripts and Viterbi variants

are described. Section 4 concerns how one might

adapt atomic costs from a training corpus of same-

category neighbours via Expectation-Maximisation.

The string-case is recalled and then a brute-force, ex-

ponentially expensivemethod for adapting the param-

eters of the All-scripts distance is outlined. Whilst for

the linear case, a particular factorisation is applica-

ble which permits efﬁcient implementation of the EM

all-scripts method, we show by means of a counter-

example that for the tree case this kind of factori-

sation is not applicable, although it has been sug-

gested in (Boyer et al., 2007) that it is. This leads

to a proposed method for adapting the parameters of

the Viterbi-script distance, something which is feasi-

ble. Section 5 then reports some experimental out-

comes obtained with this EM procedure for adapting

the Viterbi-script distance.

Emms M. (2012).

ON STOCHASTIC TREE DISTANCES AND THEIR TRAINING VIA EXPECTATION-MAXIMISATION.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 144-153

DOI: 10.5220/0003864901440153

 SciTePress

2 NON-STOCHASTIC SEQUENCE

AND TREE DISTANCES

Let us begin by formulating some deﬁnition relation

to the familiar notion of string-distance. The formu-

lations follow closely those of (Ristad and Yianilos,

1998) and are chosen to allow an easy transition to

the stochastic case.

Let S be an alphabet. Let the set of edit operation

identiﬁers, EdOp, be deﬁned by

EdOp = ((S ∪{l } ) × (S ∪ {l }))\hl ,l i

and let an edit-script be a sequence e

...e

#, n ≥ 0,

with each e

∈ EdOp and with # as a special end-of-

script marker. Given an edit-script A , it can be pro-

jected into a ’source’ string src(A ) ∈ S

∗

, by contenat-

ing the left elements of the contained operations, and

likewise into a ’target’ string trg(A ) ∈ S

∗

src(#) = e trg(#) = e

src(hl ,yiA ) = src(A ) trg(hx,l iA ) = trg(A )

src(hx,yiA ) = x src(A ) trg(hx,yiA ) = y trg(A )

The yield of edit-script A can be deﬁned as pair

of strings hsrc(A ),trg(A )i. If (s,t) = yield(A ), each

∈ A is interpretable as an edit operation in a process

of transforming s to t: deletion (a,l ), insertion (l , b),

or match/substitution (a, b). Let E(s,t) be all scripts

which yield (s,t). The multiple scripts in E(s,t) de-

scribe alternative ways to transform s into t.

If costs are deﬁned for such edit-scripts, a string-

distance between s and t can be deﬁned as the cost of

the least-cost script in E(s,t).

Alternatively one can consider the partial, 1-to-

1, order-respecting mappings from s to t. Costs can

be deﬁned for such mappings and a distance mea-

sure deﬁned via minimising these costs. Script-based

and mapping-based deﬁnitions are equivalent (Wag-

ner and Fischer, 1974): fundamentally an edit-script

is viewable as a particular serialisation of a mapping.

For ordered, labelled trees, the analogue to stan-

dard string distance was ﬁrst considered by (Tai,

1979). We develop the deﬁnitions relevant to this

below, starting ﬁrst with a mapping-based deﬁnition.

The equivalent script-based deﬁnition follows this.

A Tai mapping is a partial, 1-to-1 mapping s from

the nodes of source tree S to a target tree T which re-

spects left-to-right order and ancestry

. For the pur-

pose of assigning a score to such a mapping it is con-

venient to identify three sets:

So if (i

, j

) and (i

, j

) are in the mapping, then (T1)

le ft(i

) iffle ft( j

, j

) and (T2) anc(i

) iff anc( j

, j

)

M the (i, j) ∈ s : the ’matches’ and ’swaps’

D the i ∈ S s.t. ∀ j ∈ T,(i, j) 6∈ s : the ’deletions’

I the j ∈ T s.t. ∀i ∈ S,(i, j) 6∈ s : the ’insertions’

Where S is the label alphabets of source and target

trees, let g (i) be the label of node i. Let C be a cost

table of dimensions |S | + 1 × |S | + 1. The cost of a

mapping is the sum over the atomic costs deﬁned by

for (i, j) ∈ M cost is C [g (i)][g ( j)]

for i ∈ D cost is C [g (i)][0]

for j ∈ I cost is C [0][g ( j)]

The so-called unit-cost matrix, C

has 0 on the diag-

onal and 1 everywhere else. For a given cost matrix

C , the Tai- or tree-distance D (S,T) is deﬁned as the

cost of the least-costly Tai mapping s between S and

There is an alternative, more procedural deﬁnition

route, via tree-edit operations analogous to string-edit

operations. The table below depicts the three edit op-

erations:

operation script element

l (x

d)~r)

→ (m

d~r)

(x,l )

d~r)

→ (m

l (y

d)~r)

(l ,y)

x y

l (x

d)~r)

→ (m

l (y

d)~r)

(x,y)

Thus deletion involves making the daughters of some

node x into the daughters of that node’s parent m,

insertion involves taking some of the daughers of a

node m and making them instead the daughters of a

newdaughter y of m, and swapping/matching involves

simply replacing some node x with a node y at the

same position.

The right-hand column shows the script element

which is used to record the use of particular edit op-

eration. Using the same table of cost C as was used

for costing a mapping, a cost can be assigned to the

script describing the operations to transform a tree S

into a tree T, and a script-based deﬁnition of distance

then given via minimising this cost.

The mapping- and script-based deﬁnitions are

equivalent (Tai, 1979; Kuboyama, 2007), with a script

serving as a serialised representation of a mapping.

(Zhang and Shasha, 1989) provided an efﬁcient algo-

rithm for its calculation.

See also (Emms and Franco-Penya, 2011) in these pro-

ceedings.

To illustrate, below is shown ﬁrst a mapping be-

tween two trees, and second the sequence of edit-

operations corresponding to it, with some of the inter-

mediate stages as these operations are applied; with

unit-costs the distance is 3

ba b

a b

ba b

a b

(b,b)(a,a)(b,b)(.,a)

(b,b)(a,.)

(a,c)

a b

b b

It is easy to see that for strings encoded as linear,

vertical trees, the string-distance and tree-distance co-

incide. We will use tree-distance and Tai-distance in-

terchangeably, though the literature contains several

other, non-equivalent notions bearing the name tree-

distance. Based, as it is, simply on the notion of map-

pings respecting the two deﬁning dimensions of trees,

the Tai distance seems a particularly compelling no-

tion.

3 STOCHASTIC SEQUENCE AND

TREE DISTANCES

(Ristad and Yianilos, 1998) introduced a probabilis-

tic perspective on string distance, deﬁning a model

which assigns a probability to every possible edit-

script. Edit-script compoments e

∈ EdOp∪ {#} are

pictured as generated in succession, independently of

each other. There is an emission probability p on edit-

script components, such that

e∈EdOp∪{#}

p(e) = 1,

and a script’s probability is deﬁned by

P(e

... e

) =

p(e

)

For a given string pair (s,t), as before E(s,t) de-

notes all the edit-scripts which have (s,t) as their

It is worth noting that for the equivalence between

mapping-based costs and script-based costs, the scripts

which correspond to mappings mention each source and tar-

get symbol exactly once. Thus the ’short’ script segments

shown in the picture are not representative of the scripts

which correspond to a mapping

yield. They then deﬁne the all-paths stochastic edit

distance, P

(s,t), as the sum of the probabilities of all

scripts e ∈ E(s,t), whilst the viterbi version P

(s,t) is

the probability of the most probable one.

It is natural to consider to what extent the proba-

bilistic perspectiveadopted for string-distance by Ris-

tad and Yianilos can be applied to tree-distance. The

simplest possibility is to use exactly the same model

of edit-script probability, which leads to the notions:

Deﬁnition 1 (All-scripts stochastic Tai similari-

ty/distance). The all-scripts stochastic Tai similarity,

(S,T), is the sum of the probabilities of all edit-

scripts which represent a Tai-mapping from S to T.

The all-scripts stochastic Tai distance, D

(S,T), is its

negated logarithm, ie.

−D

(S,T)

= Q

(S,T)

Deﬁnition 2 (Viterbi-script stochastic Tai similari-

ty/distance). The Viterbi-script stochastic Tai similar-

ity, Q

(S,T), is the probability of the most proba-

ble edit-script which represents a Tai-mapping from

S to T. The Viterbi-script stochastic Tai distance,

(S,T), is its negated logarithm, ie.

−D

(S,T)

= Q

(S,T)

For Q

and Q

the probabilities on each possi-

ble component of an edit script, EdOp ∪ {#}, must

be deﬁned. In a similar fashion to the non-stochastic

case, let this be deﬁned by a table C

of dimensions

|S | + 1 × |S | + 1 such that:

for hx,yi ∈ S × S p(hx,yi) = C

(x,y)

for x ∈ S p(hx,l i) = C

(g (i),0)

for y ∈ S p(hl , yi) = C

(0,g ( j))

p(#) = C

(0,0)

For convenience C

(0,0) is interpreted as p(#). The

sum over all the entries in this table should be 1. It

is clear that an equivalent cost-table C

can be de-

ﬁned, containing the negated logs of the C

entries,

and that D

(S,T) can be equivalently deﬁned by an

additive scoring of the scripts using the entries in C

Therefore D

(S,T) coincides with the standard no-

tion of tree-distance

if the cost-table is restricted to

be the image of a possible probability-table under the

negated logarithm mapping. We will call such tables

stochastically valid cost tables. Again it is easy to see

that with sequences encoded as vertical trees, these

notions coincide with those deﬁned on sequences by

Ristad and Yianilos.

(S,T) will include a contribution from the negated

log of p(#). As all pairs will share this contribution, any

application ranking pairs can ignore this contribution.

For the Viterb-script distance D

(S,T), the well

known Zhang/Shasha algorithm is an implementa-

tion. The Viterbi-script similarity Q

can also be ob-

tained by a variant replacing + with ×. Implementing

the All-script distance D

(S,T) (or equivalent simi-

larity Q

(S,T)) turns out though to require one sub-

tle change to the original Zhang/Shasha formulation.

This is explained at further length below.

Figure 1 gives an algorithm for D

and D

. To dis-

cuss it ﬁrst some deﬁnitions from (Zhang and Shasha,

1989) are required. The algorithm operates on the

left-to-right post-order traversals of trees. If k is the

index of a node of the tree, the left-most leaf, l(k), is

the index of the leaf reached by following the left-

branch down. For a given leaf there is a highest

node of which it is the left-most leaf and any such

node is called a key-root. For any tree S, KR(S) is

the key-roots ordered by position in the post-order

traversal. If i is the index of a node of S, S[i] is the

sub-tree of S rooted at i (i.e. all nodes n such that

l(i) ≤ n ≤ i). Where i is any node of a tree S, for

any i

with l(i) ≤ i

≤ i, the preﬁx of S[i] from l(i) to

can be seen as a forest of subtrees of S[i], denoted

For(l(i),i

The description instantiates to two algorithms,

with x = V for Viterbi, and x = A for All-Scripts.

In both cases, it is a doubly nested loop ascending

through the key-roots of S and T, in which for each

pair of key-roots (i, j), a sub-routine tree dist

(i, j) is

called. Values in a tree-table T are set during calls to

tree dist

(i, j) and persist. Each call totree dist

(i, j)

operates on a sub-region

of the forest-table F , from

l(i) − 1,l( j) − 1 to i, j. The loop is designed so that

F [i

][ j

] is the forest-distance from For(l(i), i

) to

For(l( j), j

). F -entries do not persist between sep-

arate calls to tree dist

(i, j).

In the Viterbi case, TD

, there is no inversion

from neg-logs to probabilities, and the algorithm can

be applied when C

is an arbitrary table of atomic

costs.

It is the design of case 2 that enforces that only

Tai mappings are considered: when a forest distance

][ j

] is to be computed, the possibility that i

mapped to j

is factored into a forest+tree combina-

tion TM

= F

[l(i

) − 1][l( j

) − 1] + T

][ j

], so

that descendants of i

can only possibly match with

descendants of j

and vice-versa.

Setting x to V for Viterbi, the algorithm is almost

identical to that in (Zhang and Shasha, 1989), except

The initialisation sets the left-most column of this to

represent the pure deletion cases For(l(i), i

) to

0, and the

uppermost row to represent the pure insertion cases

0 to

For(l( j), j

)

input:

traversals S and T of two trees

a cost table C

compute KR(S), KR(T)

create table T

, size | S | × | T |

create table F

, size | S | + 1 × | T | + 1

(S,T) {

for each i ∈ KR(S) in ascending order {

for each j ∈ KR(T) in ascending order {

execute tree dist

(i, j)}

}

return

[|S|][|T|]

}

tree dist

(i, j) {

where

= l(i) − 1, j

= l( j) − 1

][ j

] = 0 initialize

for

= l(i)

= i {

][ j

] = F

− 1][ j

] +C

(g (i

),0) }

for

= l( j)

= j {

][ j

] = F

][ j

− 1] +C

(0,g ( j

)) }

for

= l(i)

= i

for

= l( j)

= j loop

= F

− 1][ j

− 1] +C

(g (i

),g ( j

))

= F

− 1][ j

] + C

(g (i

),0)

= F

][ j

− 1] + C

(0,g ( j

))

= F

[l(i

) − 1][l( j

) − 1]+T

][ j

]

:if(

l(i

) == l(i)

and

l( j

) == l( j)

)

{

][ j

] = OP

)

][ j

] = M

(∗)}

:if(

l(i

) 6= l(i)

l( j

) 6= l( j)

)

][ j

] = OP

,TM

)}

Figure 1: Viterbi and All-paths tree-distance algorithms.

Set x to V throughout for Viterbi, with OP

= min,

and x to A for All-paths, with OP

= logsum, where

logsum(x

.. .x

) = −log(

−x

)).

for the asterixed line, which in the original would be:

][ j

] = F

][ j

](∗∗)

Whereas the original (**) formula for updating the

tree table in case 1 updates it to store the true tree-

distance between S[i

] and T[ j

], the (*) variant stores

just M

, the cost of the least-cost script for an align-

ment of For(l(i

),i

) to For(l( j

), j

) in which nodes

and j

are mapped to each other. For the Viterbi

cost, (*) and (**) could be interchanged and so have

][ j

] store a cost in which i

and j

might not be

mapped to each other: in such a case when the values

in T

are called on in case 2, the TM

component

will just be equal to one or other of the I

or D

com-

ponents over which the minimum is calculated.

Reading the algorithm now with x set to A, T

and

represent the ’all-scripts’ probabilities, sums over

all scripts which serialize a Tai mapping between the

relevant trees or forests. Looking again at the aster-

ixed line, through not setting T

][ j

] = F

][ j

] is not the log of the sum of the probabilities

of all the scripts which can align S[i

] and T[ j

] but in-

stead the sum over all the cases in which i

is mapped

to j

. For the subsequent use of T

in case 2, this is

now a necessary feature: if T

][ j

] does not have

this interpretation then when these values are called

upon in case 2, probabilities of scripts ending in either

deletion of i

or insertion of j

are doubly counted.

Example. Let t

= t

= (b (b) (a b)), and suppose

the cost-table to the right below, which represents as

negated logs the assumptions that all probabilites are

0 except for p(a,l ) = 1/8 = p(l ,a), p(b, b) = 1/4,

and p(#) = 1/2. The left is the only Tai-mapping

which is associated with a non-zero probability edit-

script in this setting

l a b

l 1 3 inf

a 3 inf inf

b inf inf 2

By inspection, Q

) = (1/2)

(1/64),

) = (1/2)

(1/128), and these are the

values, or rather their negated logs, which will be

calculated

by the algorithm in Figure 1. However,

if T

][a

] were to include the probabilities for

scripts involving the deletions or insertions of a,

) would be incorrectly calculated to be

(1/2)

(3/64).

As a ﬁnal remark concerning the algorithm for the

Viterbi case, it is straightforward to extend the algo-

rithm so that it returns not just the cost of the best

script but also the best script itself. Hence we shall

write (v,V) = TD

(S,T).

4 EM FOR COST ADAPTATION

As noted in section 1, a possible use of a distance

measure is for deployment in a k-NN classiﬁer, deter-

mining a category for a test item based on its distances

to examples in a pre-categorised example set. This is

the case in the experiments reported on in section 5.

In those experiments the categorised items are the

syntax-structures of natural language questions, and

the categories are broad semantic categories, such as

HUM

(’the question expects a human being to be iden-

tiﬁed as the answer’) or

LOC

(’the question expects a

The reason for the premultiplying (1/2)

factor in these

numbers is that it is easier in this case to calculate ﬁrst ig-

noring p(#) and from a table in which all entries are twice

as large, and thento correct for the over-estimation; the only

scripts making any contribution all have length 5

location to be identiﬁed as the answer’).

For the tree-distance measures, the performance

of the classiﬁer is going to vary with the atomic pa-

rameter settings in the cost-table C

. One might ex-

pect that scripts between pairs of trees (or strings)

that belong to the same category differ from scripts

between pairs of trees (or strings) that belong to dif-

ferent categories. For example, for the question-

categorisation scenario, on same-category pairs one

might expect that the substitution (who/when) to

be less frequent that the substitution state/country.

In terms of the parameters of the stochastic dis-

tances this would correspond to P(who,when) <<

P(state,country), or equivalently in terms of negated

logs, C

(who,when) >> C

(state,country). This

leads to the idea that one might be able to use

Expectation-Maximisation techniques (Dempster et

al., 1977) to adapt edit-probs from a corpus of same-

category nearest neighbours.

adaptation

of costs

nearest

same−category

neighbours

Such a technique, for the case of stochastic string

distance, was ﬁrst proposed by (Ristad and Yianilos,

1998).

4.1 All-scripts EM

As a ﬁrst step towards a cost-adaptation algorithm,

consider the following brute-force all-scripts EM al-

gorithm, EM

, consisting in interations of the fol-

lowing pair of steps

(Exp)

generate a virtual corpus of scripts by treat-

ing each training pair (S,T) as standing for all the

edit-scripts s , which can relate S to T, weighting

each by its conditional probability P(s /Q

(S,T),

under current probalities C

(Max) apply maximum likelihood estimation to the

virtual corpus to derive a new probability table.

A virtual count or expectation g

S,T

(op) contributed by

S, T for an operaton op can be deﬁned by

S,T

(op) =

s :S7→T

[

P(s )

(S,T)

× freq(op ∈ s )]

and the (Exp)

accumulating these values g

S,T

(op)

for all possible op’s over all training pairs. The pic-

ture below attempts to illustrate this for a particular

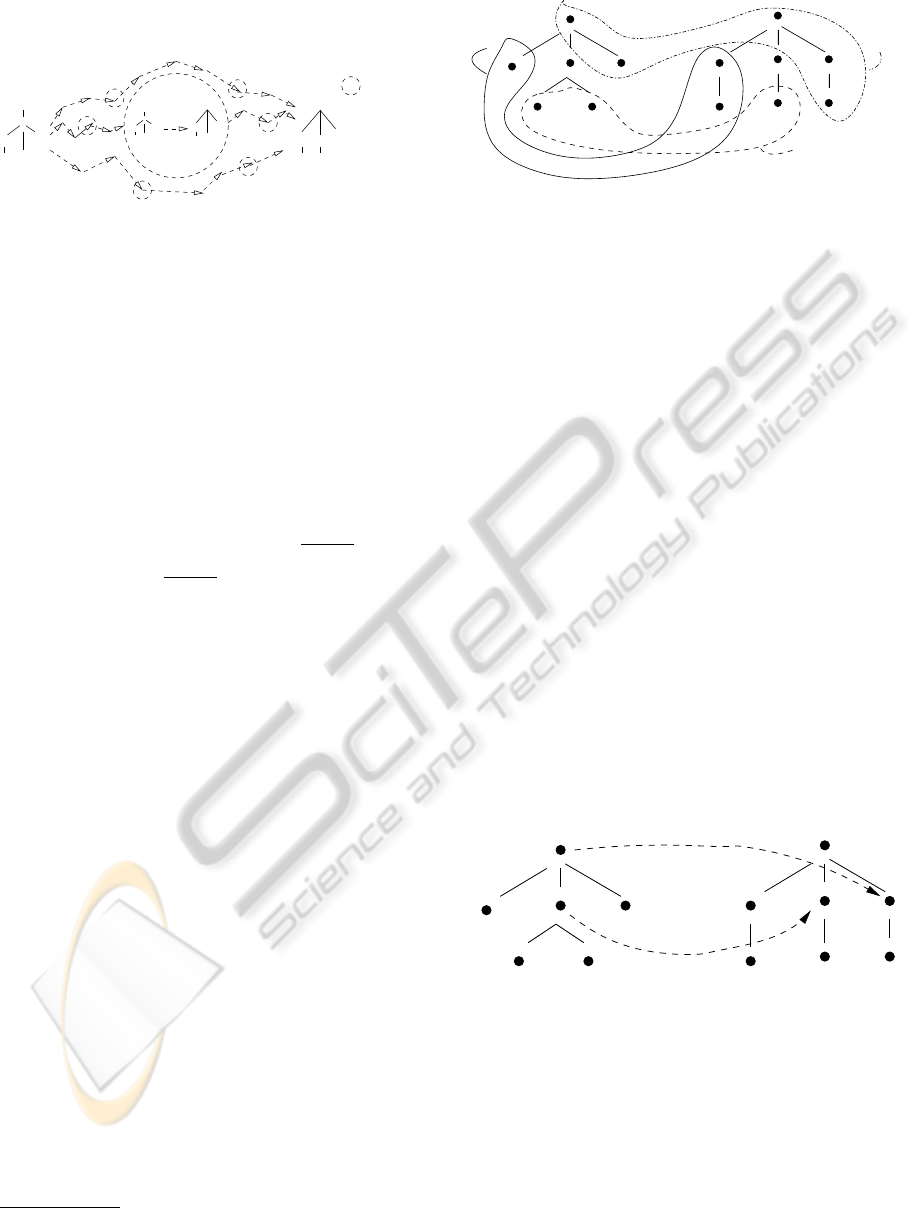
operation (a,l ) occuring in various scripts between a

particular tree pair

a b

b b

)P(

= occ. of (a,.)

(a,.)

a b

b b

For the case of linear trees, this amounts to the same

adaptation proposal as that put forward by (Ristad

and Yianilos, 1998). This brute-force algorithm is

exponentially expensive. To obtain a feasible equiv-

alent algorithm one may attempt to apply the same

strategy as that used by (Ristad and Yianilos, 1998)

for the case of linear trees, which is for each tree

pair (S,T), to ﬁrst compute position-dependent ex-

pectations g

(S,T)

[i][ j](op) for each operation and then

sum these position-independent expectations to give

the expecations per-pair g

(S,T)

(op). In this approach,

(S,T)

[i][ j](m,m

′

), the expectation for a swap (m, m

′

)

at (i, j) has the semantics

(S,T)

[i, j](m,m

′

) =

s ∈E(S,T ),(m

′

)∈s

[

p(s )

(S,T)

]

(S,T)

s ∈E(S,T),(m

′

)∈s

[p(s )]

or in words, it is the sum over the conditional prob-

abilities of any script s containing a m

′

substitu-

tion, given that it is a script between S and T.

For the case of linear trees, the position-

dependent expectations g

(S,T)

[i][ j] can be computed

feasibly because ﬁrstly, the summation in the above

can be factorised into a product of 3 terms

s ∈E(S,T),(m

′

)∈s

[p(s )]

pre

∈E(S

1:1−1

1:j−1

)

[p(s

pre

)]×

p(m,m

′

)×

suf f

∈E(S

i+1:I

j+1:J

)

[p(s

suf f

)]

(1)

and secondly the summations over the possible scripts

preﬁxing (m

′

), and the possible scripts sufﬁxing

′

) can be straightforwardly calculated; the ﬁrst

is the all-scripts algorithm, and the second an easily

formulated ’backwards’ variant.

For the case of general trees (as opposed to linear

trees) (Boyer et al., 2007) propose such a factorisa-

tion approach. Their proposal turns out, however, to

be unsound, factorizing the problem in a way which

is invalid giventhe ancestry-preservationaspect of Tai

mappings

. To explain this, consider Figure 2, which

reproduces the essentials of an example from their pa-

per

A fact which they concede p.c.

Fig. 3 p61

3 5

2 3

m’

(i)

(ii)

(iii)

Figure 2: The swap-case in expectation calculation.

For the pair of trees, we wish to calculate the position-

dependent expectation g [4,4](m,m

′

). (Boyer et al.,

2007) propose an algorithm implying the correctness

of the factorisation

s ∈E(S,T),(m

′

)∈s

[p(s )]

∈E([(·

)],(·

(·

)))

[p(s

)]× [(i)]

∈E([(·

)(·

)],[(·

)])

[p(s

)] × p(m,m

′

) [(ii)]

∈E([(·

(·

))],[(·

(·

)))])

[p(s

)] [(iii)]

(2)

where the terms (i)–(iii) corresponds to the indicated

regions in Figure 2. The problem is with ﬁnal term

(iii) in the product. Each edit-script s ∈ E(S, T) rep-

resents a Tai mapping between S and T. The summa-

tion

s ∈E(S,T),(m

′

)∈s

[p(s )] refers to those scripts

which represent a Tai mapping with the property that

is mapped to m

′

. This means that if an ances-

tor of m

is in the mapping (ie. not deleted) then

its image under the mapping must be an ancestor of

′

, and vice-versa. The ﬁnal term in the product,

∈E([·

(·

)],[·

(·

))])

[p(s

)], sums over any script

between these two sub-trees of S and T and this will

include scripts in which node ·

of S is mapped to ·

of T, and this corresponds to a mapping in which an

ancestor of m

is mapped to a non-ancestor of m

′

3 5

2 3

m’

For example if the only non-zero probability script

from (·

(·

)) to (·

(·

))) is one mapping the ·

S to the ·

of T then g [4, 4](m,m

′

) should be zero,

though according to (2) it will not be.

For general trees, a feasible equivalent to the

brute-force EM

remains an unsolved problem.

4.2 Viterbi EM

An approximation to the the All-scripts proposal con-

sists in simply in replacing the Exp

step by

(Exp)

generate a virtual corpus of scripts by treat-

ing each training pair (S,T) as standing for

the best edit-script s , which can relate S to

T, weighting it by its conditional probability

P(s )/Q

(S,T), under current costs C

Where V is the best-script, the virtual count or expec-

tation g

S,T

(op) contributedby S, T for the operaton op

would in this case be deﬁned by

(S,T)

(op) =

(S,T)

× freq(op ∈ V )

and the (Exp)

step accumulates these values

(S,T)

(op) for all possible op’s over all training pairs.

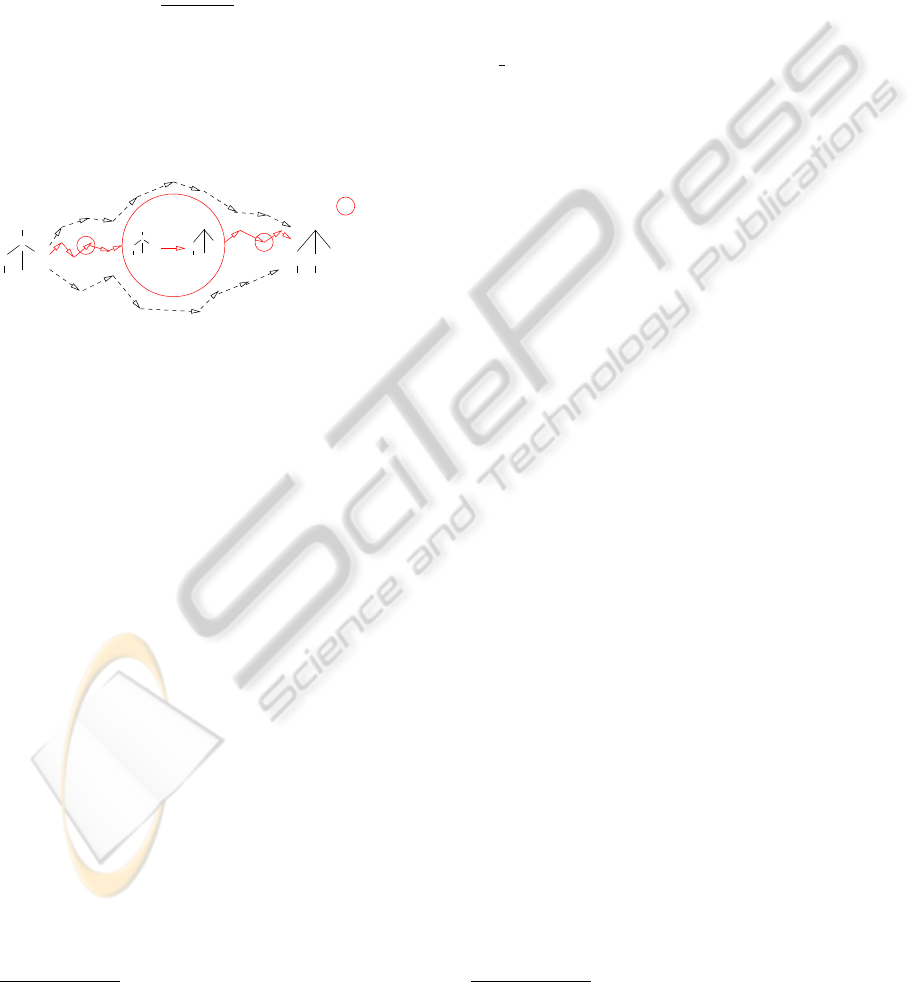
The picture below attempts to illustrate this for a par-

ticular operation (a, l ) occuring on the best-path V

between a particular tree pair

a b

b b

V)P(

(a,.)

a b

b b

= occ. of (a,.)

on best−path V

)P(

=SQ

Figure 3 spells out this Viterbi cost-adaptation algo-

rithm for stochastic tree-distance.

input:

a set P of tree pairs (S,T)

a cost table C, size |S | + 1 × |S | + 1

create tables g ,C

new

same size as C

while(

conv 6= true

)

{

zero all entries in g

for each

(S,T) ∈ P {

let

(v, V ) = TD

(S,T), a = TD

(S,T)

g [l ][l ]

−v

−a

for each

(x,y) ∈ EdOp {

g [x][y]

( freq o f (x, y) in V ) × 2

−v

−a

}

new

= −log(g /sum(g ))

new

6= C){C = C

new

} else {conv = true}

}

return

Figure 3: Viterbi EM cost adaptation for tree-distance. Note

S is the label alphabet of the tree-pairs in P . The algorithms

and TD

are as deﬁned in Figure 1.

Such Viterbi training variants have been found

beneﬁcial, for example in the context of parameter

training for PCFGs (Bened´ı and S´anchez, 2005).

Simple modiﬁcations of the algorithm as formulated

force it to generate a symmetric expectation table g .

5 EXPERIMENTS WITH VITERBI

EM COST-ADAPTATION

We have conducted some experiments with this

Viterbi EM cost-adaptation approach. In particular

we have considered how it might adapt a tree-distance

measure that is put to work in a k-NN classiﬁcation

algorithm.

Figure 4 outline the distance-weighted kNN clas-

siﬁcation algorithm which was used in the experi-

ments.

knn class(

Examples,C

;T)

{

let D = SORT({(S,D

(S,T)) | S ∈ Examples }

while(!resolved)

{

P = top(k, D ), V = weighting( P )

if(

no winner in V

)

{

set k = k + 1

}

else

{

resolved = true

}

return

category with highest vote in V

}

Figure 4: Distance-weighted k nearest neighbour classiﬁca-

tion.

top(k,D ) basically picks the ﬁrst k items from D

The weighting converts the panel of distance-rated

items to weighted votes for their categories, and in the

experiments reported later, the options for the con-

version of an item of category C, at distance d, into

a vote vote(C,d) are Majority: vote(C, d) = 1; Du-

dani: vote(C, d) = (d

max

− d)/(d

max

− d

min

), or 1 if

max

= d

min

, where d

max

and d

min

are maximum and

minimum distances in the panel (Dudani, 1976).

It can arise that the test tree T contains a symbol

for which C

has no entry. One option is to assign

all operations involving the symbol some default cost

k . See the Appendix for a proof that the ordering of

neigbours is independent of the value chosen for k

In applying the EM

cost-adaptation in the con-

text of the k-NN classiﬁcation algorithm, the training

set for cost-adaptation was taken to consists of tree

pairs (S,T), where for each example-set tree S, T is a

nearest same-category neighbour. The training algo-

rithm should less the stochastic tree-distance between

these trees.

like all other EM algorithms needs an ini-

tialisation of its parameters. We will use C

(d) for

a ’uniform’ initialisation with diagonal factor d. This

will mean that C

(d) is a stochastically valid cost-

table, with the additional properties that (i) all diag-

onal entries are equal (ii) all non-diagonal entries are

equal (iii) diagonal entries are d times more probable

Modulo some niceties concerning ties which space pre-

cludes detailing

than non-diagonal. For these purposes the cost-table

entry for p(#) is treated as non-diagonal. As an illus-

tration, for an alphabet of just 2 symbols, the initiali-

sations C

(d) for d = 3, 10, 100, and 1000 are:

3 l a b

l 3.7 3.7 3.7

a 3.7 2.115 3.7

b 3.7 3.7 2.115

10 l a b

l 4.755 4.755 4.755

a 4.755 1.433 4.755

b 4.755 4.755 1.433

100 l a b

l 7.693 7.693 7.693

a 7.693 1.05 7.693

b 7.693 7.693 1.05

1000 l a b

l 10.97 10.97 10.97

a 10.97 1.005 10.97

b 10.97 10.97 1.005

As a smoothing option concerning a table C

de-

rived by EM

, let C

be its interpolation with the

original C

(d) as follows

−C

[x][y]

= l (2

−C

[x][y]

) + (1− l )(2

−C

(d)[x][y]

)

with 0 ≤ l ≤ 1, with l = 1 giving all the weight to the

derived table, and l = 0 giving all the weight to the

initial table.

The dataset used was a natural language process-

ing one, being a corpus of (broadly) semantically cat-

egorised, and syntactically analysed questions, which

was created by from two pre-existing datasets. Ques-

tionBank (QB) is a hand-corrected treebank for ques-

tions (Judge et al., 2006; Judge, 2006b), (Judge,

2006a). A substantical percentage of the questions

in QB are taken from a corpus of semantically cat-

egorised, syntactically unannotated questions (CCG,

2001). From these two corpora we created a corpus

of 2755 semantically categorised, syntactically anal-

ysed questions, spread over the semantic categories as

follows

Cat HUM ENTY DESC NUM LOC ABBR

N 647 621 533 461 455 38

% 23.48 22.54 19.35 16.73 16.52 1.38

For further details of the software and data see

(Emms, 2011). Figure 5 shows some results of a

ﬁrst set of experiments, with unit-costs and then with

some stochastic variants. For the stochastic variants,

the cost initialisation was C

(3) in each case. All

the experiments followed a stratiﬁed 10-fold cross-

validation approach. The data was randomly split into

10 equal size folds, with approximately equal distri-

bution of the categories in each. Then in turn each

fold has taken as the test data, and the remaining 9

folds used as the example set. When cost-adaptation

was applied this means that the training pairs for EM

come from the example set. The ﬁgure shows re-

See (CCG, 2001) for details of the semantic category

labels

sults using the Dudani-voting variant of k-NN; the

Majority-voting variant was less effective.

k values

% accuracy

1 5 10 20 30 50 100 200

40 43 46 49 52 55 58 61 64 67

untrained stochasticuntrained stochastic

trained stochastic unsmoothed

trained stochastic smoothed

unit costs

Figure 5: Categorisation performance with unit costs and

some stochastic variants.

The ﬁrst thing to note is that performance with unit-

costs (▽, max. 67.7%) exceeds performance with the

non-adapted C

(3) costs (◦, max. 63.8%). Though

not shown, this remains the case with far higher set-

tings of the diagonal factor. Performance after ap-

plying EM

to adapt costs (△, max. 53.2%) is

worse than the initial performance (◦, max. 63.8%).

A Leave-One-Out evaluation, in which example-set

items are categorised using the method on the remain-

der of the example-set, gives accuracies of 91% to

99%, indicating EM

has made the best-scripts con-

necting the training pairs too probable, over-ﬁtting the

cost table. The vocabulary is sufﬁciently thinly spread

over the training pairs that its quite easy for the learn-

ing algorithm to ﬁx costs which make almost every-

thing but exactly the training pairs have zero proba-

bility. The performance when smoothing is applied

(+,max. 64.8%), interpolating the adapted costs with

the initial cost, with l = 0.99, is considerably higher

than without smoothing (△), attains a slightly higher

maximum than with unadapted costs (◦), but is still

worse than with unit costs (▽).

The following is a selection from the top 1% of

adapted swap costs.

8.50 ? .

8.93 NNP NN

9.47 VBD VBZ

9.51 NNS NN

9.78 a the

11.03 was is

11.03 ’s is

12.31 The the

12.65 you I

13.60 can do

13.83 many much

13.92 city state

13.93 city country

For the data-set used, these learned preferences are to

some extent intuitive, exchanging punctuation marks,

words differing only by capitalisation, related parts of

speech (VBD vs VVZ etc), verbs and their contrac-

tions and so on. One might expect this discounting of

these swaps relative to others to assist the categorisa-

tion, though the results reported so far indicate that it

did not.

Recall that the cost-table for the stochastic edit

distance is a representation of probabilites, with prob-

abilities represented by their negated base-2 loga-

rithms. A 0 in this case represents the probability

1. Because in a stochastically valid cost table, the

sum over all the represented probabilities must be 1,

a single 0 entry in a cost table implies inﬁnite cost

entries everywhere else. This means that a stochasti-

cally valid cost table cannot have zero costs on the

diagonal, which is the situation of the unit-cost ta-

ble, C

. This aspect perhaps mitigates against suc-

cess. The diagonal factor d in the cost initialisation

is designed to make the entries on the diagonal more

probable than other entries, but even with very high

values for d, indicating a high ratio between the diag-

onal and off-diagonal probabilities, the diagonal costs

are not negligible. This means that the unit-cost set-

ting, C

, which is clearly ’uniform’ in a sense, is not

directly emulated by the ’uniform’ stochastic initiali-

sations C

(d). The performance with the unadapted

uniform stochastic initialisation was below the perfor-

mance with unit-costs. Although results in Figure 5

show just the outcomes with C

(3), this remained the

case with far larger values of the diagonal factor d.

This invites consideration of outcomes if a ﬁnal step

is applied in which all the entries on the cost-table’s

diagonal are zeroed. In work on adapting cost-tables

for a stochastic version of string distance used in du-

plicate detection, (Bilenko and Mooney, 2003) used

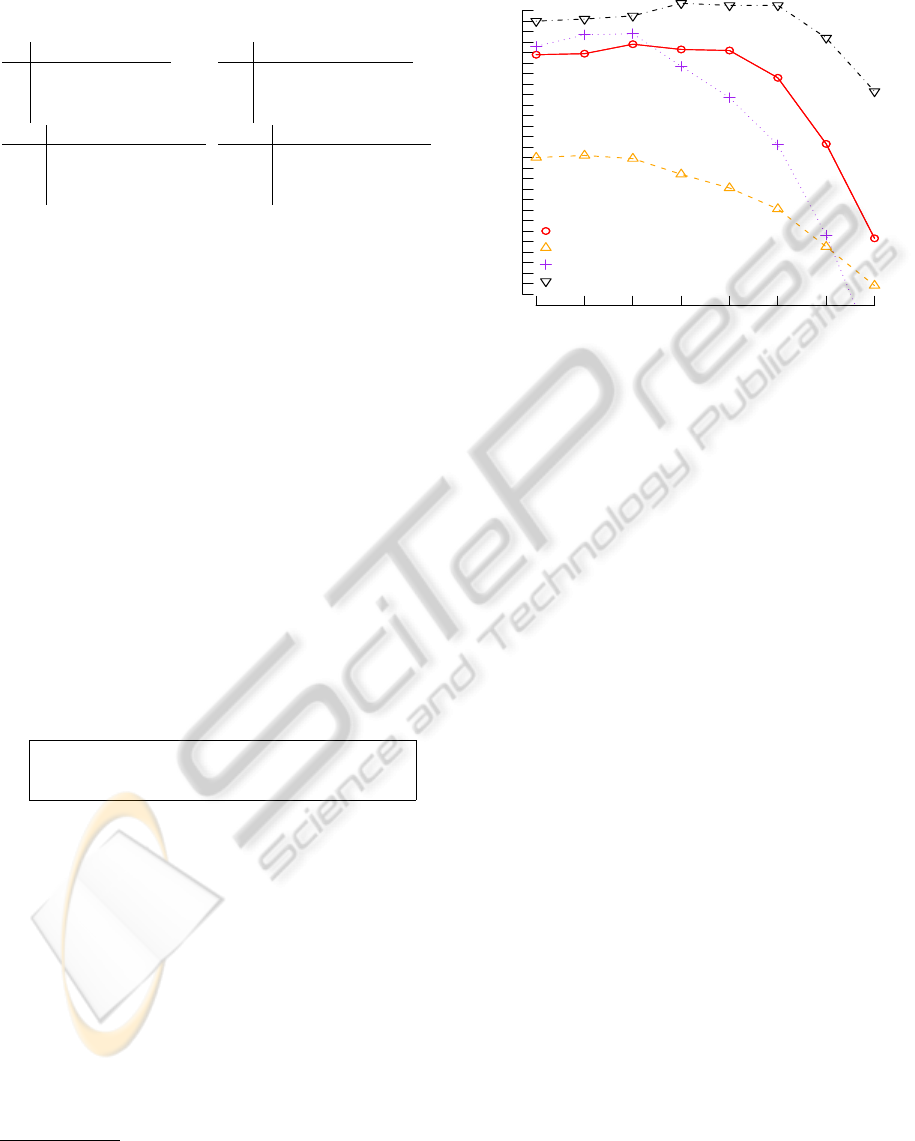
essentially this same approach. Figure 6 shows out-

comes when the trained and smoothed costs ﬁnally

have the diagonal zeroed.

The (▽) series once again shows the outcomes with

unit-costs. In this experiment, with the diagonal

zeroed, this is necessarily also the outcome ob-

tained with any unadapted uniform stochastic ini-

tialisation C

(d). The other lines in the plot

show the outcomes obtained with costs adapted by

, smoothed at varius levels of interpolation (l ∈

{0.99, 0.9, 0.5,0.1}) and with the diagonal zeroed.

Now the unit costs base-line is clearly out-performed,

the best result being 72.5% (k = 20, l = 0.99), as

compared to 67.5% for unit-costs (k = 20). Also bet-

ter results are obtained with the higher levels of the

interpolation factor, indicating greater weight given to

the values obtained by EM

and less to the stochastic

initialisation.

k values

% accuracy

1 5 10 20 30 50 100 200

60 62 64 66 68 70 72

lam 0.99lam 0.99

lam 0.9

lam 0.5

lam 0.1

unit costs

Figure 6: Categorisation performance: adapted costs with

smoothing and zeroing.

6 CONCLUSIONS

One can tentatively conclude on the basis of these ex-

periments that the Viterbi EM cost-adaptation can in-

crease the performance of a tree-distance based clas-

siﬁer, and improve it to above that attained in the unit-

cost setting, though this does require smoothing of de-

rived probabilites and a ﬁnal step of zeroing the diag-

onal.

Experiments with further data-sets is required.

One type of data of interest would be the digit-

recognition data-set represented by a tree-encoding

of outline looked at by (Bernard et al., 2008). It

would also be interest to look at applications not

to do with categorisation per-se. For example, in

the NLP-related tasks of question-answering and en-

tailment recognition, the aim is assess pairs of sen-

tences for their likelihood to be a question-answer or

hypothesis-conclusion pair. A training set of such

pairs could also serve as potential input to the cost

adaptation algorithm.

Alignments between different pairs of trees can

end up being represented by the same edit-script. A

minimal example is that the script (a, A)(b,B)(c,C)

can serve to connect both the pairs (t1,t2) and

(t1

′

,t2

′

), where:

t1 : (c(a)(b)) t2 : (C(A)(B))

′

: (c(b(a))) t2

′

: (C(B(A)))

Therefore the All-script and Viterbi-script

stochastic edit-distances are only a step towards a

fully ﬂedged generative model of aligned trees. A

fully-ﬂedged model would include further factors

to divide the probability P(a,A) × P(b,B) × P(c,C)

between the tree-pairs. A direction for further work

is the investigation of such a model of aligned trees,

and how it relates to some other recent proposals

concerning adaptive tree measures such as (Takasu et

al., 2007), (Dalvi et al., 2009)

ACKNOWLEDGEMENTS

This research is supported by the Science Foundation

Ireland (Grant 07/CE/I1142) as part of the Centre for

Next Generation Localisation (www.cngl.ie) at Trin-

ity College Dublin.

REFERENCES

Bened´ı, J.-M. and S´anchez, J.-A. (2005). Estimation of

stochastic context-free grammars and their use as lan-

guage models. Computer Speech and Language,

19(3):249–274.

Bernard, M., Boyer, L., Habrard, A., and Sebban, M.

(2008). Learning probabilistic models of tree edit dis-

tance. Pattern Recogn., 41(8):2611–2629.

Bilenko, M. and Mooney, R. J. (2003). Adaptive duplicate

detection using learnable string similarity measures.

In Proceedings of the Ninth ACM SIGKDD Interna-

tional Conference on Knowledge Discovery and Data

Mining (KDD-2003), pages 39–48.

Boyer, L., Habrard, A., and Sebban, M. (2007). Learning

metrics between tree structured data: Application to

image recognition. In Proceedings of the 18th Euro-

pean Conference on Machine Learning (ECML 2007),

pages 54–66.

CCG (2001). corpus of classiﬁed questions by Cog-

nitive Computation Group, University of Illinois

l2r.cs.uiuc.edu/∼cogcomp/Data/QA/QC.

Dalvi, N., Bohannon, P., and Sha, F. (2009). Robust web ex-

traction: an approach based on a probabilistic treeedit

model. In SIGMOD 09: Proceedings of the 35th

SIGMOD international conference on Management of

data, pages 335–348, New York, NY, USA. ACM.

Dempster, A., Laird, N., and Rubin, D. (1977). Maximum

likelihood from incomplete data via the em algorithm.

J. Royal Statistical Society, B 39:138.

Dudani, S. (1976). The distance-weighted k-nearest neigh-

bor rule. IEEE Transactions on Systems, Man and Cy-

bernetics, SMC-6:325–327.

Emms, M. (2011). Tree-distance code and datasets reported

on in experiments www.scss.tcd.ie/Martin.Emms/

TreeDist.

Emms, M. and Franco-Penya, H.-H. (2011). On order

equivalences between distance and similarity mea-

sures on sequences and trees. In Proceedings of

ICPRAM 2012 International Conference on Pattern

Recognition Application and Methods.

Judge, J. (2006a). Corpus of syntactically annotated ques-

tions http://www.computing.dcu.ie/jjudge/qtreebank/.

Judge, J. (2006b). Adapting and Developing Linguistic Re-

sources for Question Answering. PhD thesis, Dublin

City University.

Judge, J., Cahill, A., and van Genabith, J. (2006). Ques-

tionbank: creating a corpus of parse-annotated ques-

tions. In ACL 06: Proceedings of the 21st Interna-

tional Conference on Computational Linguistics and

the 44th annual meeting of the ACL, pages 497–504,

Morristown, NJ, USA. Association for Computational

Linguistics.

Kuboyama, T. (2007). Matching and Learning in Trees.

PhD thesis, Graduate School of Engineering, Univer-

sity of Tokyo.

Ristad, E. S. and Yianilos, P. N. (1998). Learning string edit

distance. IEEE Transactions on Pattern Recognition

and Machine Intelligence, 20(5):522–532.

Tai, K.-C. (1979). The tree-to-tree correction problem.

Journal of the ACM (JACM), 26(3):433.

Takasu, A., Fukagawa, D., and Akutsu, T. (2007). Statisti-

cal learning algorithm for tree similarity. In ICDM 07:

Proceedings of the 2007 Seventh IEEE International

Conference on Data Mining, pages 667672, Washing-

ton, DC, USA. IEEE Computer Society.

Wagner, R. A. and Fischer, M. J. (1974). The string-tostring

correction problem. Journal of the Association for

Computing Machinery, 21(1):168–173.

Zhang, K. and Shasha, D.(1989). Simple fast algorithms for

the editing distance between trees and related prob-

lems. SIAM Journal of Computing, 18:1245–1262.

APPENDIX

Proof Concerning Out of Table Costs

Let C

be a cost-table associated with a given label

alphabet S , let T be a tree with n symbols 6∈ S , and let

k be a ﬁxed, out-of-table cost for any (x,u), where x ∈

S ∪ {l }, u 6∈ S . Suppose S is a tree whose labels are

in S . Every s ∈ E(S,T) involve n out-of-table events.

SupposeV is the least-cost script, with cost cost

(V ).

Now suppose under a higher setting of k

′

for out-of-

table costs, that V

′

6= V is the least-cost script, so

cost

′

) < cost

′

(V ). But recosting according to k

gives cost

′

) < cost

(V ), which contradicts min-

imality of V under k . So the minimal script is in-

variant to changes of k , and D

′

(S,T) − D

(S,T) =

n× (k − k

′

). It follows that neighbour ordering is in-

variant to changes of k .