SINGLE SNAPSHOT SYSTEM FOR THE FAST 3D MODELING

USING DYNAMIC TIME WARPING

Luis Ruiz, Xavier Mateo, Ciro Gr`acia and Xavier Binefa

Department of Information and Communication Technologies, Universitat Pompeu Fabra, Barcelona, Spain

Keywords:

3D Reconstruction, Mesh Zippering, Non-overlapping, Dynamic Time Warping.

Abstract:

In this work we explore the automatic 3D modeling of a person using images acquired from a range camera.

Using only one range camera and two mirrors, the objective is to obtain a full 3D model with one single

snapshot. The combination of the camera and the two mirrors give us three non-overlapping meshes, making

impossible to use common zippering algorithms based on overlapping meshes. Therefore, Dynamic Time

Warping algorithm is used to ﬁnd the best matching between boundaries of the meshes. Experimental results

and error evaluations are given to show the robustness and efﬁciency of our method.

1 INTRODUCTION

Nowadays we can ﬁnd on the market low cost range

cameras which allow the direct retrieval of depth in-

formation from a scene. This depth information can

be used in combination with the visual information

from another sensor in order to recreate the observed

scene in a 3D environment with high realism. The

increasing use of this kind of cameras has attracted

interest from different research ﬁelds like computer

vision, computer graphics, archeology, industrial pro-

totyping, etc.

The work presented in this paper describes the

development of a real-time 3D modeling system us-

ing only one range camera and with only one camera

snapshot. This system has been mainly designed for

human body reconstruction, although any other ob-

jects could also be applied. The resulting 3D model

can be used not only for 3D rendering, but also can be

stored as an avatar for the person and physical simu-

lations could be applied (for example, application of

clothing pieces).

Our system consists of two main phases: data ac-

quisition and mesh generation. In the data acquisition

phase the 3D information of the whole model is ac-

quired trying to minimize the needed space and the

time consumed. In the mesh generation phase we an-

alyze the method for creating a closed mesh based on

the choices in the data acquisition.

The structure of the presented system is as fol-

lows: in Section 2 a review of existing similar sys-

tems is presented. Section 3 shows some preliminary

aspects needed for the correct understanding of the

presented system, which is explained in Section 4.

Experimental results of the presented system are ex-

plained in Section 5, and ﬁnally conclusions and fu-

ture work are discussed in Section 6.

2 STATE OF THE ART

The 3D modeling of common objects is a long-time

studied ﬁeld both in computer vision and in com-

puter graphics literature. Current technologies and

specially the new acquisition devices in the market

have allowed a high improvement on the result and in

the time requirements in order to obtain a full 3D rep-

resentation. Nowadays, we can ﬁnd complete systems

that try to do this work almost automatically.

One of the most well-known systems is the one

present in the internet service Photosynth, which cor-

responds to the study presented in (Snavely et al.,

2006). The main advance in this study was the pos-

sibility of detecting and matching 2D keypoints from

very different images (regardless of the viewpoint or

the camera used), registering them and therefore mak-

ing possible their placement in a 3D environment.

Also in the ﬁeld of 3D modeling from 2D im-

ages it must be taken into account the work presented

in (Pan et al., 2009). With a simple video camera

and a rotating object in front of it, the presented sys-

tem tracks different keypoints of the image along the

sequence, applying afterwards a bundle adjustment

317

Ruiz L., Mateo X., Gràcia C. and Binefa X..

SINGLE SNAPSHOT SYSTEM FOR THE FAST 3D MODELING USING DYNAMIC TIME WARPING.

DOI: 10.5220/0003867003170326

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 317-326

ISBN: 978-989-8565-04-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

(Hartley and Zisserman, 2004) which iteratively re-

ﬁnes the 3D placement of this keypoints. In a second

phase, the paper uses a variant of Delaunay triangula-

tion to obtain the ﬁnal mesh of the object.

Despite these already explained works, current ap-

proaches mainly make use of the so-called range cam-

eras, which provide a depth image in addition to the

usual visible image. One of the ﬁrst integral systems

using this kind of cameras was the work presented in

(Rusinkiewicz et al., 2002), including the acquisition,

registration, surface triangulation and ﬁnal rendering.

Its main drawback was the need of user manipulation

in some aspects of the process, producing in addition

a higher time consumption.

A more recent approach using range cameras is

presented in (Weise et al., 2011). This paper also con-

tains the whole process of the 3D modeling, from the

acquisition to the ﬁnal rendering, and solves most of

the problems present in (Rusinkiewicz et al., 2002),

in part thanks to the computer processing advance be-

tween both papers.

It must be taken into account that all the literature

available nowadays requires the rotation of the object

around its own axis, or equivalently, the rotation of the

camera. These both possibilities are not suitable for

our application, since the rotation of a person could

produce small movements in his body and the rotation

of a camera around the person requires a huge need of

space.

3 PRELIMINARY WORK

3.1 Camera Used: Microsoft Kinect

The range camera used during experiments is the Mi-

crosoft Kinect, recently released. The Kinect device

has a RGB camera, an IR camera and one laser-based

IR projector. In order to obtain the range image, this

camera does not use the method of Time Of Flight

(Gokturk et al., 2004), but triangulation between cap-

tured image and a known pattern missed by sensor.

While the laser-based IR projector emits a mesh of IR

light to the scene, the IR camera captures the distance

of every point of the IR mesh emitted by the projector.

For a typical Kinect, the resulting RGB image has

a resolution of 640 x 480 pixels, and the depth im-

age has a resolution of 320 x 240 pixels. The IR and

RGB cameras are separated by a small baseline so

they must be calibrated between themselves. How-

ever, since this is a common used range camera, the

values of the calibration are well known by the com-

munity.

Images obtained with the Microsoft Kinect are

Figure 1: Sequence of the scanning process using a turning

table example. Only 4 scans are shown, but the sequence

can be composed by a large number of scans. For each scan,

the RGB image and the depth image is shown.

noisy and static objects tend to be detected with dif-

ferent range in consecutive captures. In addition, the

device has problems in detecting object contours and

usually small structures could not be detected. For

these reasons the depth image should usually be ﬁl-

tered in order to avoid these inconveniences.

The resulting 3D image after using the Kinect is

a set of 3D points, without any surface information.

However, thanks to the known IR pattern emitted by

the sensor it is simple to directly connect the neighbor

3D points and make a fast triangulation.

3.2 Problems with Existing Approaches

In the literature exist different ways to solve the pro-

posed problem of 3D modeling. In this work we study

only the two more relevant ones: the turntable ap-

proach and the multiple cameras approach.

3.2.1 Turntable Approach

The most common method used in 3D modeling con-

sists on placing the object on a turning table, allowing

the capture of the object from several viewpoints. The

3D sensor can be ﬁxed in an appropriate place and

successive 3D captures of the object are obtained dur-

ing its rotation. The result of this scanning process is

a set of partial scans of the object, including both the

depth and the RGB information. An example using a

model person is shown in Figure 1.

Once the different partial scans have been ob-

tained, the multiple views are registered together in

order to obtain a full-side representation. For this pur-

pose usually a 2-step method is used, starting with

the so-called pairwise registration between pairs of

partial scans (Besl and McKay, 1992), followed by

the multiview registration, which makes use of the lo-

cal information of multiple pairwise registrations and

minimizes the global registration error (Sharp et al.,

2004), (Shih et al., 2008).

However, this kind of acquisition method is not

suitable for human modeling. Minimal movements of

the subject during his rotation can produce errors in

the ﬁnal registration. Also, many people are reluctant

to be rotated and this can be a problem for a possible

commercial product.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

318

Figure 2: Three viewpoints surrounding the person at each

120 degrees.

3.2.2 Multiple Range Cameras Approach

Another possible solution for the human modeling

would be the use of multiple range cameras surround-

ing the person like is shown in Figure 2. Although in

the ﬁgure only three cameras are shown, this number

could be increased. The main advantage of this ap-

proach is that the person should not be moved, avoid-

ing then their possible movements.

The main problem of having three Kinects run-

ning at the same time is that, as explained in section

3.1, the range camera projects an IR pattern over the

scene and later compares the deformation of this pat-

tern against it stored pattern. If there are more than

one range camera projecting different IR patterns at

the same time, interferences between them can exist.

A possible solution would be to take snapshots of the

scene for every range camera but at different times so

the IR patterns should not interfere.

However, although this has a simple implementa-

tion it requires a lot of space on the scene. In order to

capture the whole height of a medium height person

every range camera must be at around 3 meters away

from the object and these 3 meters of radius should

not contain any occluding object.

4 PROPOSED APPROACH

The system proposed in this paper is mainly com-

posed of two different phases: the model acquisition

phase where the 3D points of the person are cap-

tured, and the mesh triangulation and zippering phase,

where the mesh is created from the set of 3D points.

4.1 First Phase: Model Acquisition

First phase for the presented system consists in the

acquisition of the 3D points from the person. We pro-

pose a novel method using only one range camera and

two mirrors, making possible to acquire all the nec-

essary information with one single snapshot, and re-

ducing also the space requirements of the previously

explained approaches.

Figure 3: Reﬂection of a single point on the mirror. The

original point is placed in front of the mirror, and the inci-

dent ray indicating the view of the camera aims to the mir-

ror and can see the original point thanks to the reﬂection.

However, the depth camera only detects a distance to the

point, and this distance is placed in straight line according

to the direction of the incident ray. According to the ideal

reﬂection rules, the angle α between the incident ray and

the normal plane is equal to the angle β produced between

the reﬂected ray and the normal plane. In the same way, the

angle γ is equivalent to the angle δ, and therefore d

and d

have the same distance.

4.1.1 Mirrors Behavior with the Range Cameras

In order to solve the proposed problem we present a

novel approach that makes use of two standard mir-

rors which reﬂect both IR and visible light.

A standard mirror reﬂects the visible light, but it

also reﬂects the IR light. If we place a Microsoft

Kinect in front of a mirror, the IR pattern emitted by

the camera reﬂects in the mirror and therefore the sen-

sor is able to capture the 3D structure of the objects

present in the reﬂection. This method has however

a little disadvantage which can be easily solved: the

range camera does not recognize that this is a reﬂected

pattern, so it will place the reﬂected 3D structure in

straight line, i.e., at the other side of the mirror.

A simple explanationfor a single point is shown in

Figure 3. As it can be seen in the ﬁgure, the Microsoft

Kinect will place the distance to the point in straight

line and therefore the refracted point will be placed

at the other side of the mirror. According to the ideal

reﬂection rules, this new refracted point will be placed

in perfect symmetry regarding the original point with

respect to the mirror plane.

Applying this theoretical idea to our study case,

we can see the frontal view and the two reﬂected

views of a person in Figure 4. As expected, the re-

ﬂected 3D structures are placed accordingly at the

other side of the mirror.

The main advantage of this technique is that it re-

duces the total need of space. As the ﬁeld of view of

the Kinect camera is enough for capturing the whole

mirror, the IR pattern is already extended in the reﬂec-

SINGLE SNAPSHOT SYSTEM FOR THE FAST 3D MODELING USING DYNAMIC TIME WARPING

319

(a) (b)

(c)

Figure 4: In (a), the RGB image and the depth image ob-

tained from Kinect are shown (objects with a depth higher

than a threshold have been ﬁltered out for a better under-

standing). Fusing the information of both images we can

represent the 3D model of the scene, shown in (b) and (c).

Although it can not be seen in (b), in (c) is clearly seen that

the reﬂected parts of the person are placed at the other side

of the mirrors.

Figure 5: Example of the acquisition process setup. Using

the reﬂection of the mirrors, the rest of the body can be

inferred.

tion plane and therefore we do not need the additional

space behind the person. An schema of the ﬁnal dis-

position of the elements is shown in Figure 5, where

the total space needed is signiﬁcantly lower than in

Figure 2 and more appropriate for small spaces (for

example a dressing room).

However, using this technique an important dis-

advantage arises. Due to the extra distance that the

IR pattern has to travel when it reﬂects in the mirror,

the 3D resolution of this pattern will be slightly lower

when it illuminates the posterior part of the person. In

consequence the posterior views of the 3D modeled

person will have a lower resolution in comparison to

the frontal view, giving us a model which is not uni-

form in all its surface.

Another disadvantage that must be taken into ac-

count is that using this mirrors technique, we will al-

ways obtain three point sets without overlapping re-

gions between them. If a point of the scanned surface

is illuminated by the direct IR pattern and a reﬂected

IR pattern, both patterns will interfere themselves and

therefore the range camera will not be able to decide

which is the correct range. In fact, this is the same

effect as if an object is illuminated by two range cam-

eras at the same time or when a camera aims directly

at another range camera.

4.1.2 Mirror’s Plane Detection and Registration

In order to deal with the mirrors, we ﬁrst need to de-

tect where they are. For this purpose, the ﬁrst step that

we have to do is to detect some points on the mirror

frame, which will be denoted by P = {p

}. This point

detection can be achievedby a manual selection of the

points or using an automatic process for detecting the

lines corresponding to the frames.

The selected points of the mirror P = {p

} are

used in order to obtain the basis matrix M

which

converts points from the mirror reference frame to the

world reference frame. M

is computed from the

three eigenvectors (~a,

b,~c) obtained after applying the

Singular Value Decomposition of the covariance ma-

trix of P:









(1)

Note that the ﬁrst two eigenvectors with higher

eigenvalues (~a,

b) estimate the plane subspace of the

points P = {p

} and the third eigenvector (~c) is the

estimation of the plane’s normal direction.

As stated before, we need to invert the reﬂection

produced by the mirror. Since this is a reﬂection, we

only need to apply a ﬂip on the z axis for each point

with respect to the plane described by the mirror’ssur-

face. If we have a point p

in world coordinates, to

express it into mirror coordinates we apply

= M

−1

− c

) (2)

, where c

corresponds to the centroid of all the frame

points P = {p

} which belong to this mirror.

Now that the point is in mirror coordinates, for

ﬂipping the z axis we apply:

′

= (p

, p

,−p

) (3)

Once we have ﬂipped the z axis, the new point

′

is positioned on the mirror but in mirror coordi-

nates. To transform from mirror to world coordinates

we use:

′

= (M

′

) + c

(4)

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

320

4.2 Second Phase: Mesh Triangulation

and Zippering

After the model acquisition phase a set of registered

3D points is obtained. In order to obtain a real 3D

model of the person a closed mesh is needed, so in this

second phase this requirement is achieved using two

complementary techniques: mesh-based triangulation

and zippering.

4.2.1 Mesh-based Triangulation

The reconstruction of meshes from a set of 3D points

is a long-time studied subject in the computer graph-

ics literature. Although existing methods produce

good results, they usually require a set of 3D points

with low noise and, if possible, with a uniform reso-

lution along the object. Images obtained with the Mi-

crosoft Kinect camera are noisy and in addition the

use of mirrors produces an irregular resolution due to

the extra distance caused by the reﬂection, so the tri-

angulation of the set of 3D points obtained from the

acquisition phase usually gives a non-satisfactory re-

sult.

However, the use of Kinect camera has an im-

portant advantage for our purposes. As previously

stated in Section 3 the image obtained can be fast tri-

angulated thanks to the ordered 3D points obtained

by the IR pattern. In one single image of the sensor

we can obtain three different meshes at a time (the

frontal mesh and the two posterior meshes which will

be obtained from the mirrors), so the triangulation

must be done before the mirror projection happens

because although after projection the position of the

vertices change, the local connectivity between each

other does not. In Figure 6 we can see two of the

meshes that we must join, which havebeen previously

fast triangulated.

4.2.2 Zippering with Dynamic Time Warping

Once the triangulation is done, it is necessary a pro-

cess for connecting the 3 meshes generated: frontal,

back-left and back-right. In the literature we can ﬁnd

some works related to stitching meshes: (Turk and

Levoy, 1994), (Soucy and Laurendeau, 1995), (Sappa

and Garcia, 2000). Although these methods produce

good results, all of them are focused on overlapping

meshes. However, as previously explained in Section

3, in our system the three meshes cannot overlap. In

addition, it must be taken into account that a major

problem for this zippering is the presence of meshes

with different resolution, due to the fact that both back

meshes are obtained with a higher traveled distance

of the IR pattern. In order to solve these problems a

Figure 6: Frontal mesh and back-right mesh. Views are

intentionally separated in Z axis for better comprehension.

novel approach for mesh zippering based on Dynamic

Time Warping is proposed.

Dynamic Time Warping (called DTW in the fol-

lowing) (Sakoe and Chiba, 1978) (M¨uller, 2007) is

an algorithm to ﬁnd the optimal alignment between

two sequences. It was designed to compare different

speech patterns in automatic speech recognition, but

is also usual in ﬁelds like handwriting or signature

recognition.

The objective of DTW is to compare two se-

quences X := (x

,...,x

) and Y := (y

,...,y

) of

length N and M respectively (see Figure 7). The se-

quences must be ordered, but they do not need to have

the same number of features. To compare two dif-

ferent features x ∈ X and y ∈ Y a local cost measure

c(x,y) needs to be deﬁned. The deﬁnition of this lo-

cal cost measure must be established according to the

particularities of the studied case. Evaluating the lo-

cal cost measure for each pair of elements of the se-

quences X and Y, the cost matrix C ∈ R

NxM

is ob-

tained. Having this cost matrix, the optimal alignment

between X and Y can be found by looking for the path

along C with minimal cost.

Figure 7: Time alignment of two time-dependent se-

quences. Intuitively, the sequences are warped in a non-

linear fashion to match each other. Aligned points are indi-

cated by the transversal lines.

Since mirrors are oriented vertically, the way that

the meshes must be joined is through the coronal

plane of the person, that is, the vertical plane which

divides the human body into front and back. During

the process of stitching we have to decide which side

of every mesh matches the side of the other mesh.

Thus, we need to ﬁnd the points where coronal and

sagittal plane intersect for every mesh.

For every possible match, DTW retrieves a warp-

ing matrix and an accumulated distance that brings us

SINGLE SNAPSHOT SYSTEM FOR THE FAST 3D MODELING USING DYNAMIC TIME WARPING

321

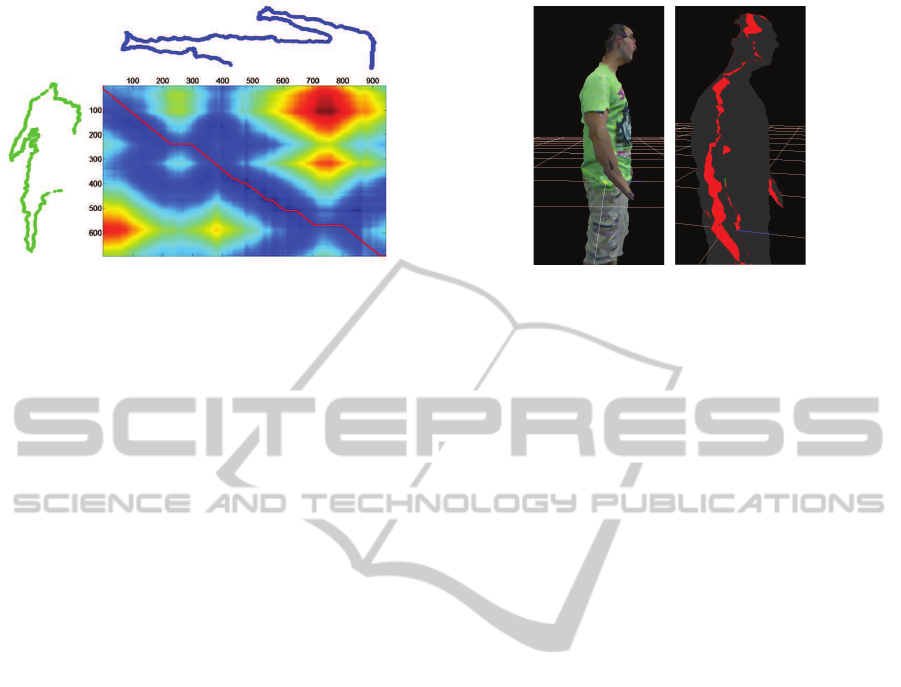
Figure 8: Cost matrix between the contour of the frontal

view (blue color) and the contour of one posterior view

(green color). As can be seen, the contour of the poste-

rior view has a lower number of points because of the extra

distance traveled by the IR pattern. In the cost matrix rep-

resentation, the red line indicates the optimal path which

produces a minimum overall cost.

the value of similarity between boundaries. In Fig-

ure 8 a distance matrix is shown, where the horizontal

axis corresponds to the ﬁrst sequence and the vertical

axis corresponds to the second one.

Once we know which parts must be stitched we

need to generate the connectivity information, creat-

ing then the faces. During the computation of DTW,

a warping matrix is generated. This warping matrix

stores the correspondences between each point of the

sequence. The warping matrix will always return the

correspondences that better match in these sequences.

In our case, we can use this information for tri-

angulating the two meshes, and the triangulation will

be straightforward. In Figure 9 we can see the model

correctly zippered by our implementation.

5 EXPERIMENTAL RESULTS

A new system for 3D modeling is proposed in this

paper. In order to evaluate the accuracy of the system

three different experiments are proposed, focusing on

the two major contributions present in this paper: the

presence of mirrors for a single snapshot 3D modeling

and the use of Dynamic Time Warping for zippering

meshes without overlap.

5.1 Loss of Information Due to the

Mirrors Reﬂection

Using a mirror to reﬂect the object helps us to reduce

the global space needed in the scene. However, a loss

of information is produced by this reﬂection, and this

loss of information affects to the ﬁnal reconstruction.

This loss can be produced either by the quality of the

Figure 9: Model stitching using DTW. In the right image is

shown, in red color, the zippered faces between the meshes.

reﬂection caused by the mirror or by the extra dis-

tance done by the IR projection which produces a loss

of quality in the generated mesh. In order to evaluate

only the loss produced by the reﬂection the following

experiment is proposed. First, the person is placed

in front of a mirror, and the 3D data produced by

the reﬂection is stored, annotating also the distance

of the camera with respect to the mirror an the dis-

tance between the mirror and the posterior part of the

person. In a second part of the experiment, without

moving the object and discarding the mirror, the cam-

era is placed behind the object (in the direction of the

reﬂection) at the same distance than the sum of the

two distances stored before. A schema of this process

can be seen in Figure 10, where the only difference

between two captures is the reﬂection of the mirror,

because the total distance will be equivalent. Having

these two 3D images available, we can now compare

both in order to see if it exists a loss in range accuracy

or in the resolution.

In order to avoid the possible movements of a per-

son between the captures in the experiment a man-

nequin will be used. In addition, to avoid the noisy

3D images produced by the Microsoft Kinect a total

amount of 10 range frames is captured in both setups

and the mean value for each 3D point is assigned.

In Figure 11 the results of this experiment are

shown. In order to compare both meshes the Haus-

dorff distance (Cignoni et al., 1998) between the

meshes is used, sampling one of the meshes and com-

puting for each sample the Hausdorff distance to the

closest point on the other mesh. Visually comparing

the 3D meshes obtained from the experiment (subﬁg-

ures 11(b) and 11(d)), it can be seen a change of the

texture color in the shirt (produced by the light re-

ﬂections in the mirror) and a loss of 3D points in the

edges of the reﬂected mesh. A clear example can be

seen in the hand, which is less deﬁned in the reﬂected

3D view in subﬁgure 11(b). This loss of resolution in

the edges is conﬁrmed after computing the Hausdorff

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

322

(a) (b)

Figure 10: For each studied object, ﬁrst the 3D of the poste-

rior part is extracted as can be seen in (a). The resulting 3D

is obtained at a distance which is equivalent to the distance

of the camera to the mirror plus the distance of the mirror to

the object. In a second phase, in (b), the mirror is discarded

and the camera is placed at the same distance but in straight

line, so the total distance will be equivalent.

distance, which is close to zero in the inner part of the

meshes and tends to be higher in the edges. The max-

imum distance between both meshes is 1,2897 cm.

and the mean distance for all the samples is 0,2083

cm.

In addition to the Hausdorff distance between

meshes, the loss of resolution due to the mirror re-

ﬂection is analyzed. The 3D mesh obtained with re-

ﬂection (subﬁgure 11(b)) has a total of 18097 vertices

and 34985 faces. On the other side, the mesh obtained

with direct capture (subﬁgure 11(d)) has 22755 ver-

tices and 44303 faces, so the percentage of loss using

a mirror is about 20%, both for vertices and faces.

5.2 Loss of Information Due to the

Extra Distance in the Mirrors

The following experiment was based on taking snap-

shots of the mannequin at different distances in order

to evaluate their possible implication in the quality of

the generated mesh. Different captures at 300, 350,

400, 450 and 500 cm. are obtained, and the results can

be seen in Figure 12. Results show that the distance

with respect to the mannequin affects to the quality

of the generated mesh, where for higher distances the

quality of the mesh is greatly reduced.

In Figure 13 the mean value of the Hausdorff

distances for each separation of the mannequin are

shown, starting from 300 cm. (which has a distance

of 0 cm. because is compared to itself) to the 500 cm.

We can observe an exponential behavior, where for

each additional 50 cm. the Hausdorff distance is near

to be doubled.

In addition to the inaccuracy produced by the dis-

tance, also the loss of vertices and faces is evaluated.

In Figure 14, a plot indicating the number of vertices

and faces for each capture is shown. We can see that

(a) (b)

(e)

Figure 11: (a) Visible image and depth image using the mir-

ror. With this information, and after computing the ﬂip of

the mirror, the obtained 3D representation is shown in (b).

Discarding the mirror and placing the Kinect at the back

side of the mannequin with the same distance, the resulting

images and the 3D representation are shown in (c) and (d).

In (e) we can see the result after comparing both 3D meshes

using the Hausdorff distance, using the same point of view

used previously and another view looking at the back.

the results ﬁts with an exponential decay model.

5.3 Evaluation of the Zippering Process

In this section we discuss results obtained with the

stitching process using Dynamic Time Warping. The

SINGLE SNAPSHOT SYSTEM FOR THE FAST 3D MODELING USING DYNAMIC TIME WARPING

323

(a) (b) (c) (d) (e)

Figure 12: At the top, captured visible image of the mannequin at 300, 350, 400, 450 and 500 cm. respectively. In the middle

row the resultant 3D meshes are shown, having a degradation of the mesh for the higher distances. At the bottom, Hausdorff

distance of the 3D meshes against the ﬁrst mesh, which is considered as reference. We can see that due to the range camera

resolution, the farther is the object, the bigger the difference.

300 cm. 350 cm. 400 cm. 450 cm. 500 cm.

0,5 cm.

1 cm.

1,5 cm.

2 cm.

2,5 cm.

3 cm.

3,5 cm.

Distance to the object

Hausdorff distance with respect to

the reference mesh

Figure 13: Mean value of the Hausdorff distance for a sep-

aration of 300 cm.(Hausdorff 0 cm.), 350 cm. (Hausdorff

0.3517 cm.), 400 cm. (Hausdorff 0.9170 cm.), 450 cm.

(Hausdorff 1.7277 cm.) and 500 cm. (Hausdorff 3.3804

cm.).

300 cm. 350 cm. 400 cm. 450 cm. 500 cm.

10.000

20.000

30.000

40.000

50.000

60.000

70.000

Distance to the object

Complexity of the obtained 3D mesh

vertices

faces

Figure 14: Relation between complexity of the mesh and

distance to the object.

objective is to evaluate the loss of information which

is produced in the 3D model due to the zippering be-

tween the 3 meshes.

Since the noise produced by the range camera

used causes random mesh generation, a reliable ex-

periment with a captured 3D model or person can-

not be done. For this, a synthetic human model is

used, splitting it in 3 parts and later zippering using

our method. The synthetic model is splitted in two

parts by the coronal plane, and afterwards the back

part is splitted again by its sagittal plane, giving us

the 3 parts obtained as we would use the mirrors.

The split of the parts is done by subtracting points

of the synthetic mesh. Since the triangulation of the

mesh depends on these 3D points, the faces composed

by the subtracted points will disappear, giving us an

irregular split which is similar to the split produced

by the mirrors.

Using the mirrors approach proposed in this paper,

in addition to the split of the model, a loss of resolu-

tion on the back of the model is produced. To emulate

this loss on the synthetic model a simpliﬁcation on

the two back meshes between 0% and 50% is done.

To evaluate the zippering result, Hausdorff distance

between the result of the zippering and the original

synthetic mesh is computed.

In Figure 15 the result of zippering the splitted

model with a loss of 40% for the posterior meshes can

be seen. As expected, Hausdorff distance increases in

the zones where there are more difference in the reso-

lution.

In order to evaluate the accuracy of the zippering

process with respect to the resolution degradation on

the back meshes, the mean value of the Hausdorff dis-

tance is analyzed for degradation of 10%, 20%, 30%,

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

324

Figure 15: Result of the zippering for a reduction of 40% for the two back meshes. Red color indicates a low Hausdorff

distance, while blue color indicates a high Hausdorff distance. In the image magniﬁcation of the head it can be seen that the

high Hausdorff distance is produced by the high difference between the resolutions of the frontal and the back mesh. In the

image magniﬁcation of the arm, a discontinuity of the mesh produce a high Hausdorff distance because the original mesh had

two triangles in this position, while our zippering process only triangulates with one triangle.

0 10 20 30 40 50

0.1 cm

0.2 cm

0.3 cm

0.4 cm

Percentage of degradation for the back meshes

Mean value of the Hausdorff distance

Figure 16: Evolution of the mean Hausdorff distance for

different degradation percentage of the back meshes.

40% and 50%. The results are displayed in Figure

16, where the evolution of the accuracy has a linear

behavior.

6 CONCLUSIONS AND FUTURE

WORK

In this work we have presented a novel system for the

efﬁcient modeling of a human body using only one

range camera and two mirrors. Our method presents

good characteristics in terms of efﬁciency, compact-

ness and low memory usage.

The experiments show that, with a low-cost range

camera like the Microsoft Kinect and two mirrors, a

fast 3D reconstruction can be done. The use of mir-

rors allows a reduction of the space needed for the

modeling, but on the other side produce a degrada-

tion on the created 3D model. This degradation is

produced by two factors: the reﬂection itself, which

produces a loss of about 20% in the number of ver-

tices and faces, and the additional distance of the IR

pattern after bouncing at the mirror.

Due to the use of the mirrors there was no overlap

between the meshes and therefore the traditional tech-

niques for stitching could not be implemented. Dy-

namic Time Warping has demonstrated that is a pow-

erful algorithm not only suitable for speech recogni-

tion, but also for many other ﬁelds.

In relation with future work, many challenges are

open and some issues should be solved. One of

these issues is the necessity to avoid the non-manifold

meshes, which could produce errors in the hole ﬁlling

algorithms. If a closed volume is achieved, accom-

plishing manifoldness, the next step could be to sub-

mit this mesh to an automatic rigging process (Baran

and Popovi´c, 2007). After this, we would have a 3D

model with a skeleton inside with every face of the

model correctly weighted respect to each bone. Us-

ing this rigged model and the skeleton-tracking capa-

bilities of Microsoft Kinect, we could move this body

SINGLE SNAPSHOT SYSTEM FOR THE FAST 3D MODELING USING DYNAMIC TIME WARPING

325

in real time and this opens the door to many applica-

tions.

Of course, another planned future work is the use

of another different range cameras, in addition to the

current Microsoft Kinect. The use of this low-cost

camera increases the availability and it is widely used

in the research ﬁeld, but it is expected to achieve

3D images with a high improvement on quality using

other possibilities.

ACKNOWLEDGEMENTS

This work was produced thanks to the support of the

Spanish Ministry of Science and Innovation, under

the project TSI-020302-2010-110.

REFERENCES

Baran, I. and Popovi´c, J. (2007). Automatic rigging and

animation of 3d characters. ACM Trans. Graph., 26.

Besl, P. and McKay, H. (1992). A method for registration

of 3-d shapes. Pattern Analysis and Machine Intelli-

gence, IEEE Transactions on, 14(2):239 –256.

Cignoni, P., Rocchini, C., and Scopigno, R. (1998). Metro:

Measuring error on simpliﬁed surfaces. Comput.

Graph. Forum, 17(2):167–174.

Gokturk, S., Yalcin, H., and Bamji, C. (2004). A time-of-

ﬂight depth sensor - system description, issues and

solutions. In Computer Vision and Pattern Recog-

nition Workshop, 2004. CVPRW ’04. Conference on,

page 35.

Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press, ISBN: 0521540518, second edition.

M¨uller, M. (2007). Information Retrieval for Music and

Motion. Springer-Verlag New York, Inc., Secaucus,

NJ, USA.

Pan, Q., Reitmayr, G., and Drummond, T. (2009). Pro-

FORMA: Probabilistic Feature-based On-line Rapid

Model Acquisition. In Proc. 20th British Machine Vi-

sion Conference (BMVC), London.

Rusinkiewicz, S., Hall-Holt, O., and Levoy, M. (2002).

Real-time 3D model acquisition. ACM Transactions

on Graphics (Proc. SIGGRAPH), 21(3):438–446.

Sakoe, H. and Chiba, S. (1978). Dynamic program-

ming algorithm optimization for spoken word recog-

nition. Acoustics, Speech and Signal Processing,

IEEE Transactions on, 26(1):43 – 49.

Sappa, A. and Garcia, M. (2000). Incremental multiview

integration of range images. In Pattern Recognition,

2000. Proceedings. 15th International Conference on,

volume 1, pages 546 –549 vol.1.

Sharp, G., Lee, S., and Wehe, D. (2004). Multiview regis-

tration of 3d scenes by minimizing error between co-

ordinate frames. Pattern Analysis and Machine Intel-

ligence, IEEE Transactions on, 26(8):1037 –1050.

Shih, S.-W., Chuang, Y.-T., and Yu, T.-Y. (2008). An efﬁ-

cient and accurate method for the relaxation of mul-

tiview registration error. Image Processing, IEEE

Transactions on, 17(6):968 –981.

Snavely, N., Seitz, S. M., and Szeliski, R. (2006). Photo

tourism: Exploring photo collections in 3d. In

SIGGRAPH Conference Proceedings, pages 835–846,

New York, NY, USA. ACM Press.

Soucy, M. and Laurendeau, D. (1995). Ageneral surface ap-

proach to the integration of a set of range views. Pat-

tern Analysis and Machine Intelligence, IEEE Trans-

actions on, 17(4):344 –358.

Turk, G. and Levoy, M. (1994). Zippered polygon meshes

from range images. In Proceedings of the 21st an-

nual conference on Computer graphics and inter-

active techniques, SIGGRAPH ’94, pages 311–318.

ACM.

Weise, T., Wismer, T., Leibe, B., and Gool, L. V. (2011).

Online loop closure for real-time interactive 3d scan-

ning. Comput. Vis. Image Underst., 115:635–648.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

326