STATIC POSE ESTIMATION FROM DEPTH IMAGES

USING RANDOM REGRESSION FORESTS AND HOUGH VOTING

Brian Holt and Richard Bowden

Centre for Vision, Speech and Signal Processing, University of Surrey, Guildford, U.K.

Keywords:

Pose Estimation, Human Body, Regression Forests, Range Image, Hough Transform, Kinect.

Abstract:

Robust and fast algorithms for estimating the pose of a human given an image would have a far reaching impact

on many ﬁelds in and outside of computer vision. We address the problem using depth data that can be captured

inexpensively using consumer depth cameras such as the Kinect sensor. To achieve robustness and speed on a

small training dataset, we formulate the pose estimation task within a regression and Hough voting framework.

Our approach uses random regression forests to predict joint locations from each pixel and accumulate these

predictions with Hough voting. The Hough accumulator images are treated as likelihood distributions where

maxima correspond to joint location hypotheses. We demonstrate our approach and compare to the state-of-

the-art on a publicly available dataset.

1 INTRODUCTION

Estimation of human pose is a problem that has re-

ceived signiﬁcant attention in recent years. A fast,

robust solution to the problem would have wide rang-

ing impact in gaming, human computer interaction,

video analysis, action and gesture recognition, and

many other ﬁelds. The problem remains a difﬁcult

one primarily because the human body is a highly de-

formable object. Aditionally, there is large variability

in body shape among the population, image capture

conditions, clothing, camera viewpoint, occlusion of

body parts (including self-occlusion) and background

is often complex.

In this paper we cast the pose estimation task as a

continuous non-linear regression problem. We show

how this problem can be effectively addressed by

Random Regression Forests (RRFs). Our approach

is different to a part-based approach since there are

no part detectors at any scale. Instead, the approach

is more direct, with features computed efﬁciently on

each pixel used to vote for joint locations. The votes

are accumulated in Hough accumulator images and

the most likely hypothesis is found by non-maximal

suppression.

The availability of depth information from real-

time depth cameras has simpliﬁed the task of pose es-

timation (Zhu and Fujimura, 2010; Ganapathi et al.,

2010; Shotton et al., 2011; Holt et al., 2011) over tra-

ditional image capture devices by supporting high a-

Figure 1: Overview: given a single input depth image, eval-

uate a bank of RRFs for every pixel. The output from each

regressor is accumulated in a Hough-like accumulator im-

age. Non-maximal suppression is applied to ﬁnd the peaks

of the accumulator images.

ccuracy background subtraction, working in low-

illumination environments, being invariant to color

and texture, providing depth gradients to resolve am-

biguities in silhouettes, and providing a calibrated

estimate of the scale of the object. However, even

with these advantages, there remains much to done to

achieve a pose estimation system that is fast and ro-

bust.

One of the major challenges is the amount of data

required in training to generate high accuracy joint es-

timates. The recent work of Shotton et al. (Shotton

et al., 2011) constructs a training set of approximately

two billion samples from one million computer gen-

erated depth images. If each value is stored in a 32

557

Holt B. and Bowden R..

STATIC POSE ESTIMATION FROM DEPTH IMAGES USING RANDOM REGRESSION FORESTS AND HOUGH VOTING.

DOI: 10.5220/0003868005570564

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 557-564

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

bit ﬂoating point number, the size of their training set

would be 14TB, which is beyond the reach of what

most researchers could store or process. Shotton et al

make use of a proprietary distributed training archi-

tecture using 1000 cores to train their decision trees.

We propose an approach that is in many ways similar

to Shotton et al’s approach, but requires signiﬁcantly

less data and processing power.

Our approach applies advances made using RRFs

reported recently in a wide range of computer vision

problems. This technique has been demonstrated by

Gall and Lempitsky (Gall and Lempitsky, 2009) to

offer superior object detection results, and has been

used successfully in applications as diverse as the es-

timation of head pose (Fanelli et al., 2011), anatomy

detection and localisation (Criminisi et al., 2011), es-

timating age based on facial features (Montillo and

Ling, 2009) and improving time-of-ﬂight depth map

scans (Reynolds et al., 2011). To the best of our

knowledge Random Regression Forests have not been

applied to pose estimation.

The contributions of this paper are the follow-

ing. First, we show how RRFs can be combined

within a Hough-like voting framework for static pose

estimation, and secondly we evaluate the approach

against state-of-the-art performance on publicly avail-

able datasets. The paper is organised as follows: Sec-

tion 2 discusses related work, Section 3 develops the

theory and discusses the approach, Section 4 details

the experimental setup and results and Section 5 con-

cludes.

2 RELATED WORK

A survey of the advances in pose estimation can be

found in (Moeslund et al., 2006). Broadly speaking,

static pose estimation can be divided into global and

local (part-based) pose estimation. Global approaches

to discriminative pose estimation include direct re-

gression using Relevance Vector Machines (Agarwal

and Triggs, 2006), using a parameter sensitive vari-

ant of Locality Sensitive Hashing to efﬁciently lookup

and interpolate between similar poses (Shakhnarovich

et al., 2003), using Gaussian Processes for generic

structured prediction of the global body pose (Bo and

Sminchisescu, 2010) and a manifold based approach

using Random Forests trained by clustering similar

poses hierarchically (Rogez et al., 2008).

Many of the state of the art approaches to pose

estimation use part-based models (Sigal and Black,

2006; Tran and Forsyth, 2010; Sapp et al., 2010) .

The ﬁrst part of the problem is usually formulated as

an object detection task, where the object is typically

an anatomically deﬁned body part (Felzenszwalb and

Huttenlocher, 2005; Andriluka et al., 2009) or Pose-

lets (parts that are “tightly clustered in conﬁgura-

tion space and appearance space”) (Holt et al., 2011;

Bourdev et al., 2010; Wang et al., 2011). The sub-

sequent task of assembly of parts into an optimal

conﬁguration is often achieved through a Pictorial

Structures approach (Felzenszwalb and Huttenlocher,

2005; Andriluka et al., 2009; Eichner et al., 2009),

but also using Bayesian Inference with belief prop-

agation (Singh et al., 2010), loopy belief propagation

for cyclical models (Sigal and Black, 2006; Wang and

Mori, 2008; Tian and Sclaroff, 2010) or a direct infer-

ence on a fully connected model (Tran and Forsyth,

2010).

Work most similar to ours includes

• Gall and Lempitsky (Gall and Lempitsky, 2009)

apply random forests tightly coupled with a

Hough voting framework to detect objects of a

speciﬁc class. The detections of each class cast

probabilistic votes for the centroid of the ob-

ject. The maxima of the Hough accumulator

images correspond to most likely object detec-

tion hypotheses. Our approach also uses Random

Forests, but we use them for regression and not

object detection.

• Shotton et al. (Shotton et al., 2011) apply an ob-

ject categorisation approach to the pose estima-

tion task. A Random Forest classiﬁer is trained

to classify each depth pixel belonging to a seg-

mented body as being one of 32 possible cate-

gories, where each category is chosen for optimal

joint localisation. Our approach will use the same

features as (Shotton et al., 2011) since they can

be computed very efﬁciently, but our approach

skips the intermediate representation entirely by

directly regressing and then voting for joint pro-

posals.

• The work of (Holt et al., 2011) serves as a natu-

ral baseline for our approach, since their publicly

available dataset is designed for the evaluation of

static pose estimation approaches on depth data.

They apply an intermediate step in which poselets

are ﬁrst detected, whereas we eliminate this step

with better results.

3 PROPOSED APPROACH

The objective of our work is to estimate the conﬁgura-

tion of a person in the 2D image plane parameterised

by B body parts by making use of a small training set.

We deﬁne the set of body parts B = {b

}

i=1

where

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

558

∈ ℜ

corresponding to the row and column of b

the image plane. The labels corresponding to B com-

prise Q = {head, neck, shoulder

, shoulder

, hip

hip

, elbow

, hand

} where |Q| = B.

The novelty in our approach is twofold. Firstly,

our approach is able to learn the relationship between

the context around a point x in a training image and

the offset to a body part b

. Given a new point x

in a

test image, we can use the learned context to predict

the offset from x

to b

. Secondly, since the image

features that we use are weak and the human body is

highly deformable, our second contribution is to use

Hough accumulators as body part likelihood distribu-

tions where the most likely hypothesis

is found us-

ing non-maximal suppression.

3.1 Image Features

We apply the randomised comparison descriptor of

(Amit and Geman, 1997; Lepetit and Fua, 2006; Shot-

ton et al., 2011) to depth images. While this is an

inherently weak feature, it is both easy to visualise

how the feature relates to the image, and when com-

bined with many other features within a non-linear re-

gression framework like Random Regression Forests

it yields high accuracy predictions. Given a current

pixel location x and random offsets φ = (u, v) |u| <

w, |v| < w at a maximum window size w, deﬁne the

feature

(I, x) = I(x +

I(x)

) −I(x +

I(x)

) (1)

where I(x) is the depth value (the range from

the camera to the object) at pixel x in image I and

φ = (x

, x

) are the offset vectors relative to x. As ex-

plained in (Shotton et al., 2011), we scale the offset

vectors by a factor

I(x)

to ensure that the generated

features are invariant to depth. Similarly, we also de-

ﬁne I(x

) to be a large positive value when x

is either

Figure 2: Image features: the most discriminative feature φ

is that which yields the greatest decrease in mean squared

error, and is therefore by deﬁnition the feature at the root

node of the tree. In (a) the pixel x is shown with these offsets

φ = (u, v) that contribute most to head

(the row) and in (b)

the offsets φ that contribute most to head

(the column).

Figure 3: Random Regression Forest: a forest is an ensem-

ble learner consisting of a number of trees, where each tree

contributes linearly to the result. During training, each tree

is constructed by recursively partitioning the input space

until stopping criteria are reached. The input subregion

at each leaf node (shown with rectangles) is then approx-

imated with a constant value that minimises the squared

error distance to all labels within that subregion. In this

toy example, the single dimension function f (x) is approx-

imated by constant values (shown in different colours) over

various regions of the input space.

background or out of image bounds.

The most discriminative features found to predict

the head are overlaid on test images in Figure 2. These

features make sense intuitively, because in Figure 2(a)

the predictions of the row location of the head depend

on features that compute the presence or absence of

support in the vertical direction and similarly for Fig-

ure 2(b) in the horizontal direction.

3.2 Random Regression Forests

A decision tree (Breiman et al., 1984) is a non-

parameteric learner that can be trained to predict cat-

egorical or continuous output labels.

Given a supervised training set consisting of p

F-dimensional vector and label pairs (S

, l) where

∈ R

, i = 1, ..., p and l ∈ R

, a decision tree re-

cursively partitions the data such that impurity in the

node is minimised, or equivalently the information

gain is maximised through the partition.

Let the data at node m be represented by Q. For

each candidate split θ = ( j, τ

) consisting of a feature

j and threshold τ

, partition the data into Q

le f t

(θ) and

right

(θ) subsets

le f t

(θ) = (x, l)|x

≤ τ

(2)

right

(θ) = Q \Q

le f t

(θ) (3)

The impurity over the data Q at node m is com-

puted using an impurity function H(), the choice of

which depends on the task being solved (classiﬁcation

or regression). The impurity G(Q, θ) is computed as

G(Q, θ) =

le f t

H(Q

le f t

(θ)) +

right

H(Q

right

(θ)) (4)

STATIC POSE ESTIMATION FROM DEPTH IMAGES USING RANDOM REGRESSION FORESTS AND HOUGH

VOTING

559

Select for each node m the splitting parameters θ

that minimise

∗

= argmin

G(Q, θ) (5)

Given a continuous target y, for node m, repre-

senting a region R

with N

observations, a common

criterion H() to minimise is the Mean Squared Er-

ror (MSE) criterion. Initially calculate the mean c

over a region

∑

i∈N

(6)

The MSE is the sum of squared differences from

the mean

H(Q) =

∑

i∈N

− c

)

(7)

Recurse for subsets Q

le f t

(θ

∗

) and Q

right

(θ

∗

) un-

til the maximum allowable depth is reached, N

min samples or N

= 1.

Given that trees have a strong tendency to overﬁt

to the training data, they are often used within an en-

semble of T trees. The individual tree predictions are

averaged

ˆy =

∑

t=0

ˆy

(8)

to form a ﬁnal prediction with demonstrably lower

generalisation errors (Breiman, 2001).

3.3 Hough Voting

Hough voting is technique that has proved very suc-

cessful for identifying the most likely hypotheses in a

parameter space. It is a distributed approach to opti-

misation, by summing individual responses to an in-

put in an parameter space. The maxima are found to

correspond to the most likely hypotheses.

Our approach uses the two dimensional image

plane as both the input and the parameter space. For

each body part q

∈ Q we deﬁne a Hough accumulator

}, ∀q ∈ Q, where the dimensions of the accumu-

lator correspond to the dimensions of the input image

I: H ∈ ℜ

× ℜ

, H = 0 for all pixels.

An example of the Hough voting step in our sys-

ten can be seen in Figure 4 where the ﬁnal conﬁgu-

ration is shown alongside the accumulator images for

the left shoulder, elbow and hand. Note that the left

shoulder predictions are tightly clustered around the

groundtruth location, whereas the left elbow is less

certain and the left hand even more so. Neverthe-

less, the weight of votes in each case are in the correct

Figure 4: Hough accumulator images: the Hough image is

a probabilistic parameterisation that accumulates votes cast

by the RRFs. The maxima in the parameterised space cor-

respond to the most likely hypotheses in the original space.

In this example the Hough accumulator shows the concen-

tration of votes cast for the (b) left shoulder, (c) left elbow

and (d) left hand.

area, leading to successful predictions shown in Fig-

ure 4(a).

3.4 Training

Before we can train our system, it is necessary to

extract features and labels from the training data.

Firstly, we generate a dictionary of F random offsets

= (u

, v

)

j=1

. Then, we construct our training data

and labels. For each image in the training set, a ran-

dom subset of P example pixels is chosen to ensure

that the distribution over the various body parts is ap-

proximately uniform. For each pixel x

in this random

subset, the feature vector S is computed as

S = f

(I, x)

j=1

(9)

and the offset o

∈ ℜ

from every x to every body

part q

= x −b

(10)

The training set is then the set of all training vec-

tors and corresponding offsets. With the training

dataset constructed, we train 2B RRFs R

i ∈ 1..B, to

estimate the offset to the row of body part b

and 2B

RRFs R

i ∈ 1..B, to estimate the offset to the column

of body part b

3.5 Test

Since the output of a RRF is a single valued contin-

uous variable, we let f (R

1,2

, I, x) be a function that

evaluates the RRF R

1,2

on image I at pixel x.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

560

Figure 5: Parameter tuning: experiments on accuracy when (a) the depth of the trees are varied, (b) the maximum offset is

varied.

Figure 6: PCP error curve against (Holt et al., 2011). Our

method clearly beats theirs for all values of r, even though

we do not impose kinematic constraints.

We apply the following algorithm to populate the

Hough parameter space H

∀q ∈ Q.

Algorithm 1: Compute probability distribution H

Input: Image I,

for each pixel x do

for each label q

∈ Q do

⇐ R

(x)

⇐ R

(x)

increment H

(x +o

, x +o

)

end for

The key idea is that for each pixel in a test image,

each RRF will be evaluated to estimate the the loca-

tion of the body part by adding the prediction (which

is the offset) to the current pixel.

4 EXPERIMENTAL RESULTS

In this section we evaluate our proposed method and

describe the experimental setup and experiments per-

formed. We compare our results to the state-of-the-

art (Holt et al., 2011) on a publicly available dataset,

and evaluate our results both quantitively and qualita-

tively.

For each body part q

∈ Q, a Hough accumula-

tor likelihood distribution is computed using Algo-

rithm 1. Unless otherwise speciﬁed, we construct our

training set from 1000 random pixels x per training

image I, where each sample has F = 2000 features

(I, x). This results in a training set of 5.2GB.

4.1 Dataset

A number of datasets exist for the evaluation of pose

estimation techniques on appearance images, for ex-

ample Buffy (Ferrari et al., 2008) and Image Parse

(Ramanan, 2006), but until recently there were no

publicly available datasets for depth image pose esti-

mation. CDC4CV Poselets (Holt et al., 2011) appears

to be the ﬁrst publicly available Kinect dataset, con-

sisting of 345 training and 347 test images at 640x480

pixels, where the focus is on capturing the upper body

of the subject. The dataset comes with annotations of

all the upper body part locations.

4.2 Evaluation

We report our results using the evaluation metric pro-

posed by (Ferrari et al., 2008): “A body part is con-

sidered as correctly matched if its segment endpoints

lie within r = 50% of the length of the ground-truth

segment from their annotated location.” The percent-

age of times that the endpoints match is then deﬁned

STATIC POSE ESTIMATION FROM DEPTH IMAGES USING RANDOM REGRESSION FORESTS AND HOUGH

VOTING

561

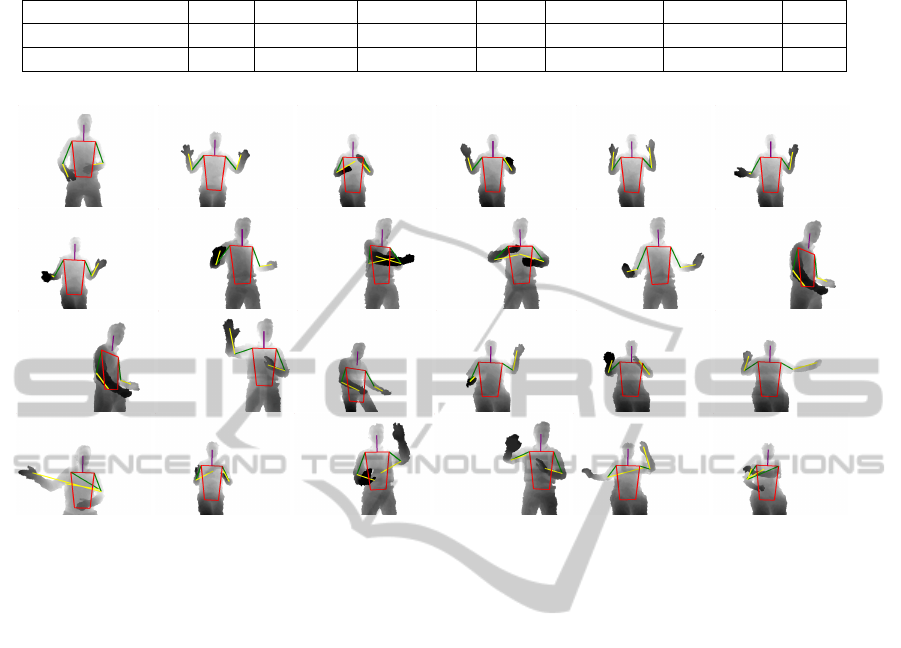
Table 1: Percentage of Correctly Matched Parts. Where two numbers are present in a cell, they refer to left/right respectively.

Head Shoulders Side Waist Upper arm Forearm Total

(Holt et al., 2011) 0.99 0.78 0.93 0.73 0.65 0.69 0.66 0.22 0.33 0.67

Our method 0.97 0.81 0.82 0.83 0.71 0.74 0.72 0.28 0.37 0.69

Figure 7: Top three rows: example predictions using the proposed method. Bottom row: Failure modes.

as the PCP. A low value for r requires to a very high

level of accuracy in the estimation of both endpoints

for the match to be correct, and this requirement is re-

laxed progressively as the ratio r increases to its high-

est value of r = 50%. In Figure 6 we show the effect

of varying r in the PCP calculation, and we report our

results at r = 50% in Table 1 as done by (Ferrari et al.,

2008) and (Holt et al., 2011). From Table 1 it can be

seen that our approach represents an improvement on

average of 5% for the forearm, upper arm and waist

over (Holt et al., 2011), even though our approach

makes no use of kinematic constraints to improve pre-

dictions.

In Figure 5(a) we show the effect of varying the

maximum depth of the trees. Note how the Random

Regression Forest trained on the training set with less

data (10 pixels per image) tends to overﬁt to the data

on deeper trees. Figure 5(b) shows the effect of vary-

ing the maximum window size w for the offsets φ.

Conﬁrming our intuition, a small window has too lit-

tle context to make an accurate prediction, whereas

a very large window has too much context which re-

duces performance. The optimal window size is 100

pixels.

Example predictions including accurate estimates

and failure modes are shown in Figure 7.

4.3 Computation Times

Our implementation in python runs at ∼ 15 seconds

per frame on a single core modern desktop CPU. The

memory consumption is directly proportional to the

number of trees per forest and the maximum depth to

which each tree has been trained. At 10 trees per for-

est and a maximum depth of 20 nodes, the classiﬁer

bank uses approximately 4 gigabytes of memory. The

code is not optimised, meaning that further speedups

could be achieved by parallelising the prediction pro-

cess since the estimates of each pixel are indepen-

dent of each other, by reimplementing the algorithm

in C/C++, or by making use of an off the shelf graph-

ics card that supports CUDA to run the algorithm in

parallel in the GPU cores.

5 CONCLUSIONS AND FUTURE

WORK

In this paper we have shown how Random Regres-

sion Forests can be combined with a Hough voting

framework to achieve robust body part localisation

with minimal training data. We use data captured

with consumer depth cameras and efﬁciently compute

depth comparison features that support our goal of

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

562

non-linear regression. We show how Random Regres-

sion Forests are trained, and then subsequently used

on test image with Hough voting to accurately pre-

dict joint locations. We demonstrate our approach and

compare to the state-of-the-art on a publicly available

dataset. Even though our system is implemented in an

unoptimised high level language, it runs in seconds

per frame on a single core. As future work we plan

to apply these results with the temporal constraints of

a tracking framework for increased accuracy and tem-

poral coherency. Finally, we would like to apply these

results to other areas of cognitive vision such as HCI

and gesture recognition.

ACKNOWLEDGEMENTS

This work was supported by the EC project

FP7-ICT-23113 Dicta-Sign and the EPSRC project

EP/I011811/1. Thanks to Eng-Jon Ong and Helen

Cooper for their insights and stimulating discussions.

REFERENCES

Agarwal, A. and Triggs, B. (2006). Recovering 3D human

pose from monocular images. IEEE Transactions on

Pattern Analysis and Machine Intelligence, 28(1):44 –

58.

Amit, Y. and Geman, D. (1997). Shape quantization and

recognition with randomized trees. Neural computa-

tion, 9(7):1545–1588.

Andriluka, M., Roth, S., and Schiele, B. (2009). Pictorial

structures revisited: People detection and articulated

pose estimation. In (IEEE Computer Society Con-

ference on Computer Vision and Pattern Recognition,

2009), pages 1014 –1021.

Bo, L. and Sminchisescu, C. (2010). Twin gaussian pro-

cesses for structured prediction. International Journal

of Computer Vision, 87:28–52.

Bourdev, L., Maji, S., Brox, T., and Malik, J. (2010). De-

tecting people using mutually consistent poselet acti-

vations. In (ECCV, 2010), pages 168 – 181.

Breiman, L. (2001). Random forests. Machine Learning,

45:5–32.

Breiman, L., Friedman, J., Olshen, R., and Stone, C. (1984).

Classiﬁcation and regression trees. Chapman and

Hall.

Criminisi, A., Shotton, J., Robertson, D., and Konukoglu,

E. (2011). Regression forests for efﬁcient anatomy

detection and localization in CT studies. In Medical

Computer Vision. Recognition Techniques and Appli-

cations in Medical Imaging, volume 6533 of Lecture

Notes in Computer Science, pages 106–117. Springer.

CVPR (2008). CVPR, Anchorage, AK, USA.

CVPR (2010). CVPR, San Francisco, USA.

CVPR (2011). CVPR, Colorado Springs, USA.

ECCV (2010). ECCV, Heraklion, Crete.

Eichner, M., Ferrari, V., and Zurich, S. (2009). Better ap-

pearance models for pictorial structures. In Proceed-

ings of the BMVA British Machine Vision Conference,

volume 2, page 6, London, UK.

Fanelli, G., Gall, J., and Van Gool, L. (2011). Real time

head pose estimation with random regression forests.

In (CVPR, 2011), pages 617 –624.

Felzenszwalb, P. and Huttenlocher, D. (2005). Pictorial

structures for object recognition. International Jour-

nal of Computer Vision, 61(1):55 – 79.

Ferrari, V., Marin-Jimenez, M., and Zisserman, A. (2008).

Progressive search space reduction for human pose es-

timation. In (CVPR, 2008), pages 1 – 8.

Gall, J. and Lempitsky, V. (2009). Class-speciﬁc hough

forests for object detection. In (IEEE Computer So-

ciety Conference on Computer Vision and Pattern

Recognition, 2009), pages 1022–1029.

Ganapathi, V., Plagemann, C., Koller, D., and Thrun, S.

(2010). Real time motion capture using a single time-

of-ﬂight camera. In (CVPR, 2010), pages 755 –762.

Holt, B., Ong, E. J., Cooper, H., and Bowden, R. (2011).

Putting the pieces together: Connected poselets for

human pose estimation. In Proceedings of the IEEE

Workshop on Consumer Depth Cameras for Computer

Vision, Barcelona, Spain.

IEEE Computer Society Conference on Computer Vision

and Pattern Recognition (2009). CVPR, Miami, FL,

USA.

Lepetit, V. and Fua, P. (2006). Keypoint recognition us-

ing randomized trees. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 28(9):1465–1479.

Moeslund, T., Hilton, A., and Kr

uger, V. (2006). A sur-

vey of advances in vision-based human motion cap-

ture and analysis. Computer Vision and Image Under-

standing, 104(2-3):90 – 126.

Montillo, A. and Ling, H. (2009). Age regression from

faces using random forests. In ICIP09, pages 2465–

2468.

Ramanan, D. (2006). Learning to parse images of articu-

lated bodies. In Proceedings of the NIPS, volume 19,

page 1129, Vancouver, B.C., Canada. Citeseer.

Reynolds, M., Dobo

s, J., Peel, L., Weyrich, T., and Brostow,

G. (2011). Capturing time-of-ﬂight data with conﬁ-

dence. In (CVPR, 2011).

Rogez, G., Rihan, J., Ramalingam, S., Orrite, C., and Torr,

P. H. S. (2008). Randomized trees for human pose

detection. In (CVPR, 2008), pages 1–8.

Sapp, B., Jordan, C., and Taskar, B. (2010). Adaptive pose

priors for pictorial structures. In (CVPR, 2010), pages

422 –429.

Shakhnarovich, G., Viola, P., and Darrell, T. (2003). Fast

pose estimation with parameter-sensitive hashing. In

Proceedings of the IEEE International Conference on

Computer Vision, page 750, Nice, France.

Shotton, J., Fitzgibbon, A., Cook, M., Sharp, T., Finocchio,

M., Moore, R., Kipman, A., and Blake, A. (2011).

Real-time human pose recognition in parts from a sin-

gle depth image. In (CVPR, 2011).

STATIC POSE ESTIMATION FROM DEPTH IMAGES USING RANDOM REGRESSION FORESTS AND HOUGH

VOTING

563

Sigal, L. and Black, M. (2006). Measure locally, reason

globally: Occlusion-sensitive articulated pose estima-

tion. In Proceedings of the IEEE Computer Society

Conference on Computer Vision and Pattern Recogni-

tion, pages 2041 – 2048, New York, NY, USA.

Singh, V. K., Nevatia, R., and Huang, C. (2010). Efﬁcient

inference with multiple heterogeneous part detectors

for human pose estimation. In (ECCV, 2010), pages

314 – 327.

Tian, T.-P. and Sclaroff, S. (2010). Fast globally optimal 2d

human detection with loopy graph models. In (CVPR,

2010), pages 81 –88.

Tran, D. and Forsyth, D. (2010). Improved human parsing

with a full relational model. In (ECCV, 2010), pages

227–240.

Wang, Y. and Mori, G. (2008). Multiple tree models for

occlusion and spatial constraints in human pose esti-

mation. In Proceedings of the European Conference

on Computer Vision, Marseille, France.

Wang, Y., Tran, D., and Liao, Z. (2011). Learning hierar-

chical poselets for human parsing. In (CVPR, 2011).

Zhu, Y. and Fujimura, K. (2010). A bayesian framework

for human body pose tracking from depth image se-

quences. Sensors, 10(5):5280 – 5293.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

564