SKETCHING FLUID FLOWS

Combining Sketch-based Techniques and Gradient Vector Flow

for Lattice-Boltzmann Initialization

Sicilia Ferreira Judice and Gilson Antonio Giraldi

National Laboratory for Scientiﬁc Computing, Petropolis, RJ, Brazil

Keywords:

Fluid Simulation, Lattice-Boltzmann Method, Gradient Vector Flow, Sketching Modeling.

Abstract:

This work proposes an intuitive ﬂuid ﬂow initialization for computer graphics applications. A combination of

sketching techniques and Gradient Vector Flow is proposed to obtain a smooth initialization for the simulation

using a Lattice Boltzmann Method (LBM). The LBM is based on the fundamental idea of constructing simpli-

ﬁed kinetic models, which incorporates the essential physics of microscopic processes so that the macroscopic

averaged properties satisfy macroscopic equations. The application of sketching techniques is proposed in

order to enable the user to draw freely the initial state of the ﬂuid ﬂow using an intuitive interface. Moreover,

it will be possible for the user to deﬁne multiply connected domains with suitable boundary conditions.

1 INTRODUCTION

In the last decades, techniques for ﬂuid simulation

have been widely studied for computer graphics ap-

plications. The motivation for such interest relies in

the potential applications of these methods and in the

complexity and beauty of the natural phenomena that

are involved. In particular, techniques in the ﬁeld

of computational ﬂuid dynamics (CFD) have been

applied for ﬂuid animation in applications such as

virtual surgery simulators (M

uller et al., 2004b), vi-

sual effects (Witting, 1999), and games (M

uller et al.,

2004a).

The traditional ﬂuid animation methods in com-

puter graphics rely on a top-down viewpoint that

uses 2D/3D mesh-based approaches motivated by the

methods of ﬁnite element (FE) and ﬁnite difference

(FD) in conjunction with Navier-Stokes equations for

ﬂuids (Foster and Metaxas, 1997; Stam, 2003). Al-

ternatively, lattice methods comprised of the Lattice

Gas Cellular Automata (LGCA) and Lattice Boltz-

mann (LBM) can be used. The basic idea behind these

methods is that the macroscopic dynamics of a ﬂuid

are the result of the collective behavior of many mi-

croscopic particles. The LGCA follows this idea, but

it simpliﬁes the dynamics through simple and local

rules for particle interaction and displacements.

On the other hand, the LBM constructs a simpli-

ﬁed kinetic model, a simpliﬁcation of the Boltzmann

equation, which incorporates the essential micro-

scopic physics so that the macroscopic averaged prop-

erties obey the desired equations (Chen and Doolen,

1998). The LBM have provided signiﬁcant successes

in modeling ﬂuid ﬂows and associated transport phe-

nomena. The methods simulate transport by tracing

the evolution of a single particle distribution through

synchronous updates on a discrete grid. Before starts

the simulation, it is necessary to deﬁne the initial con-

ditions, which can be an initial velocity ﬁeld, pressure

ﬁeld or an initial distribution of particles.

The proposal of this work is to provide an intu-

itive ﬂuid ﬂow initialization for the LBM method. To

implement this task, the LBM technique is combined

with methods of sketch-based modeling (Cook and

Agah, 2009). In this way, the user will be able to

deﬁne an initial state for the ﬂuid ﬂow through free-

hand drawing. Moreover, it will be possible to set up

holes within the ﬂuid domain in order to get a multi-

ply connected region.

A drawing canvas, which in the actual implemen-

tation is aligned with the computer screen, is provided

to the user. So, the user draws sketch paths inside

the ﬂuid domain using the mouse. Each path deﬁnes

a streamline of the ﬂuid and the corresponding tan-

gent ﬁeld is used to compute the ﬂuid velocity over

the path. Then, this ﬁrst velocity ﬁeld is used as input

to the Gradient Vector Flow (GVF) (Xu and Prince,

1997). The ﬁeld obtained by solving the GVF equa-

tions is a smooth version of the original one that tends

to be extended very far from the user deﬁned paths.

328

Ferreira Judice S. and Antonio Giraldi G..

SKETCHING FLUID FLOWS - Combining Sketch-based Techniques and Gradient Vector Flow for Lattice-Boltzmann Initialization.

DOI: 10.5220/0003868403280337

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 328-337

ISBN: 978-989-8565-02-0

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Thus, the smoothed velocity ﬁeld is used as an ini-

tial condition for the LBM method. The main con-

tribution of our work is the combination of sketching

techniques and Gradient Vector Flow for LBM initial-

ization.

The article is organized as follows. Section 2 re-

views related works. The section 3 describes the Lat-

tice Boltzmann technique. In section 4 the method-

ology of the Gradient Vector Flow is explained. Sec-

tion 5 explains the sketch-based modeling. In section

6 we describe the proposed technique. The results and

advantages of the proposed framework are shown in

section 7. Finally, section 8 gives the conclusions and

ﬁnal comments.

2 RELATED WORKS

The LBM method is based on the fundamental idea

of constructing simpliﬁed kinetic models that incor-

porate the essential physics of microscopic processes

so that the macroscopic averaged properties satisfy

macroscopic equations. The LBM is especially useful

for modeling complicated boundary conditions and

multiphase interfaces (Chen and Doolen, 1998). Ex-

tensions of this method are described, including sim-

ulations of ﬂuid turbulence, suspension ﬂows, and re-

action diffusion systems (Wei et al., 2004).

Lattice models have a number of advantages

over more traditional numerical methods, particularly

when ﬂuid mixing and phase transitions occur (Roth-

man and Zaleski, 1994). Simulation is always per-

formed on a regular grid, and can be efﬁciently im-

plemented on a massively parallel computer. Solid

boundaries and multiple ﬂuids can be introduced in a

straightforward manner and the simulation is done ef-

ﬁciently, regardless of the complexity of the boundary

or interface (Buick et al., 1998). In the case of Lattice-

Gas Cellular Automata (LGCA), there are no numer-

ical stability issues because its evolution follows inte-

ger arithmetic. For LBM, numerical accuracy and sta-

bility depend on the Mach number (max-speed/speed

of sound). The computational cost of the LGCAs is

lower than that for LBM-based methods. However,

system parametrization (e.g., viscosity) is difﬁcult to

do in LGCA models, and the obtained dynamics is

less realistic than for LBM.

To provide an intuitive modeling of the initial

conﬁguration of the ﬂuid, sketching techniques

can be applied. The ﬁrst sketch-based modeling

system was Sketchpad launched in 1963 by Ivan

Sutherland (Sutherland, 1964), who wrote ”The

Sketchpad system makes it possible for a man and a

computer to converse rapidly through the medium of

line drawings”. An early approach was to use draw-

ing input as symbolic instructions (Zeleznik et al.,

2006). This method allows a designer access to the

multitude of commands in a modeling interface, and

was well suited to the limitations of early hardware.

As technology has progressed, the evolution of these

approach leads to a system that can interpret a user’s

drawing directly (Varley et al., 2004), a system that

can use shading and tone to give a 2D drawing the

appearance of 3D volume (Williams, 1990), and

a system that can approach 3D modeling from the

perspective of sculpture in which virtual tools are

used to build up a model like clay, or cut it down with

tools like a sculptor (Bærentzen and Christensen,

2002).

The sketch-based modeling systems

SKETCH (Zeleznik et al., 2006) and Teddy (Igarashi

et al., 2007) are examples of how sketches or drawn

gestures can provide a powerful interface for fast ge-

ometric modeling. However, the notion of sketching

a motion is less well-deﬁned than that of sketching an

object. Walking motions can be created by drawing

a desired path on the ground plane for the character

to follow, for example. In (Thorne et al., 2004), the

authors present a system for sketching the motion

of a character. Recently, the work of (Schroeder

et al., 2010) proposed a sketch-based system for

creating illustrative visualizations of 2D vector ﬁelds.

The work proposed by (Zhu et al., 2011) presents

a sketching system that incorporates a background

ﬂuid simulation for illustrating dynamic ﬂuid sys-

tems. It combines sketching, simulation, and control

techniques in one user interface and can produce

illustrations of complex ﬂuid systems in real time.

Users design the structure of the ﬂuid system using

basic sketch operations on a canvas and progressively

edit it to show how ﬂow patterns change. The system

automatically detects and corrects the structural

errors of ﬂow simulation as the user sketches. A

ﬂuid simulation runs constantly in the background to

enhance ﬂow and material distribution in physically

plausible ways.

The Gradient Vector Flow (GVF) method is based

on a parabolic partial different equation (PDE) that

may be derived from a variational problem (Xu and

Prince, 1997). The method was originally proposed

for image processing applications: an initial value

problem derived from image features is associated to

that parabolic PDE (Aubert and Kornprobst, 2002).

The GVF has been applied together with active

contours models (or snakes) for boundary extraction

in medical images segmentation. Snakes are curves

deﬁned within an image domain that can move under

the inﬂuence of internal forces within the curve

SKETCHING FLUID FLOWS - Combining Sketch-based Techniques and Gradient Vector Flow for Lattice-Boltzmann

Initialization

329

itself and external forces derived from the image

data. They are used in computer vision and image

processing applications, particularly to locate object

boundaries.

The key idea of GVF is to use a diffusion-reaction

PDE to generate a new external force ﬁeld that makes

snake models less sensitive to initialization as well

as improves the snakes ability to move into bound-

ary concavities (Xu and Prince, 1997). Also, there

are results about the global optimality and numerical

analysis of GVF in the context of Sobolev spaces (Xu

and Prince, 1998). In our work we take advantage of

the GVF ability to generate a smooth version of the

original ﬁeld, that tends to be extended very far from

the paths deﬁned by the user, to get an initial velocity

ﬁeld constrained to the user sketch.

3 THE LBM METHODOLOGY

In recent years, Lattice Boltzmann Methods (LBM)

have taken the attention of the scientiﬁc community,

due to their ease of implementation, extensibility and

computational efﬁciency. Speciﬁcally in computa-

tional ﬂuid dynamic, LBM has been applied because

of its ease implementation of boundary conditions

and numerical stability in wide variety of ﬂow condi-

tions with various Reynolds numbers (Chopard et al.,

1998).

The LBM has evolved from the Lattice Gas Cellu-

lar Automata (LGCA), which, despite its advantages,

has certain limitations related to their discrete nature:

the rise of noise, which makes necessary the use of

processes involving the calculation of average val-

ues, and little ﬂexibility to adjust the physical param-

eters and initial conditions. The LBM was introduced

by (McNamara and Zanetti, 1988), where the authors

showed the advantage of extending the boolean dy-

namics of cellular automata to work directly with real

numbers representing probabilities of presence.

In the LBM, the domain of interest is discretized

in a lattice and the ﬂuid is considered as a collection

of particles. These particles move in discrete time

steps, with a velocity pointing along one of the di-

rections of the lattice. Besides, particles collide with

each other and physical quantities of interest associ-

ated with the lattice nodes are updated at each time

step. The computation of each node depends on the

properties of itself and the neighboring nodes at the

previous time step (Chopard et al., 1998; Chen and

Doolen, 1998). The dynamics of this method is gov-

erned by the Lattice-Boltzmann equation:

(~x +∆

, t + ∆

) − f

(~x,t) = Ω

( f ), (1)

with i = 1, ..., z, where z is the number of lattice direc-

tions. The f

term is a density distribution function, ~x

is the lattice node, ~c

is one of the lattice directions,

∆

is the lattice spacing, ∆

is the time step and Ω

( f )

is the collision term.

In the work presented in (Higuera et al., 1989),

the authors proposed to linearize the collision term Ω

around its local equilibrium solution:

Ω

( f ) = −



(~x,t) − f

(ρ,~u)



, (2)

where τ is the relaxation time scale and f

is the

equilibrium particles distribution that is dependent on

the macroscopic density (ρ) and velocity (~u). The

parameter τ is related to diffusive phenomena in

the problem, in this case with the viscosity of the

ﬂuid (Chen and Doolen, 1998).

The general equation of the equilibrium function

is given by (Chopard et al., 1998):

= ρω



1 +

(~c

·~u)

(~c

·~u)

−

(~u ·~u)



, (3)

where ω

are weights and c

is the lattice speed of

sound, which is dependent on the lattice.

There are different Lattice-Boltzmann models for

numerical solutions of various ﬂuid ﬂow scenarios,

where each model has different lattice discretization.

The LBM models are usually denoted as DxQy,

where x and y correspond to the number of dimen-

sions and number of microscopic velocity directions

(~c

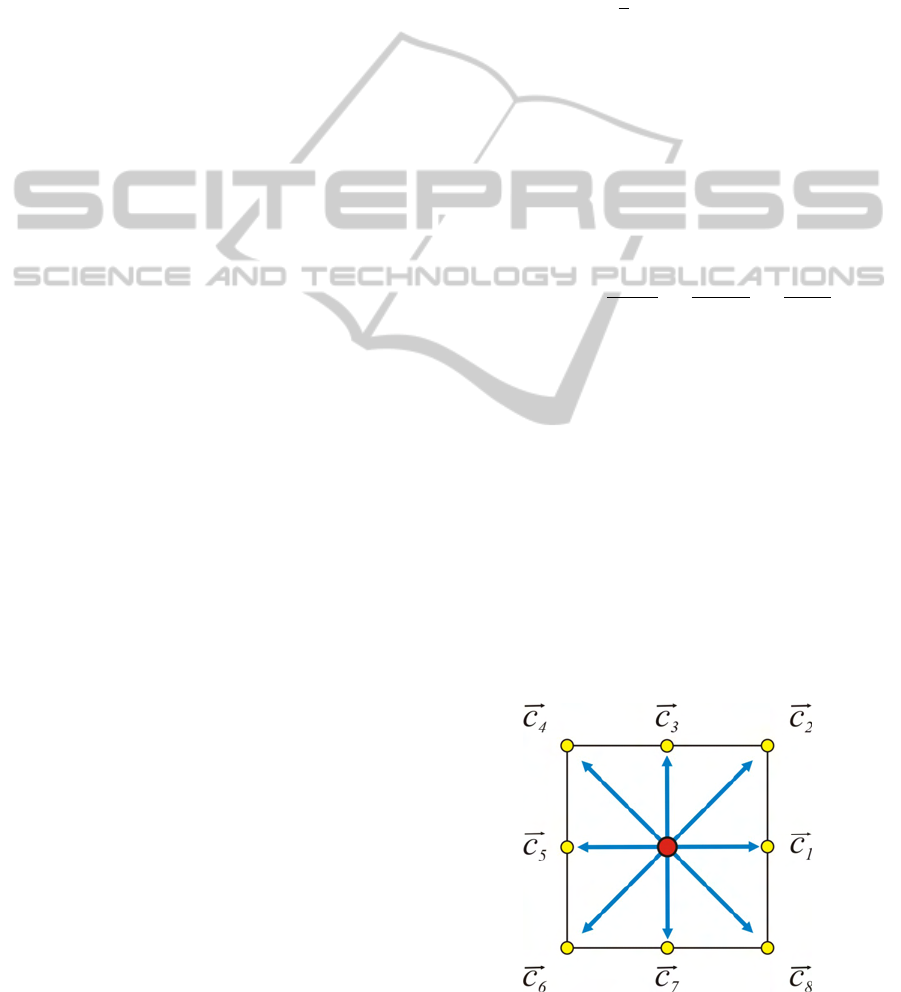
) respectively. In this work, our proposal is to

implement a two-dimensional LBM model, known

as D2Q9, which has 8 possibilities of non-zero

velocities, as shown in Figure 1.

The weights for the D2Q9 LBM model are given

Figure 1: The D2Q9 LBM node, with 8 non-zero velocities.

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

330

by:

, ω

1,3,5,7

, ω

2,4,6,8

, (4)

where ω

is related to the rest particle. Replacing (4)

in (3), gives us the equilibrium function for the D2Q9

LBM model:

= ω



ρ+ρ



(~c

·~u)

(~c

·~u)

−

(~u ·~u)



(5)

with i = 0,...,8. Our interest relies on the macro-

scopic scale, where the physical macroscopic quan-

tities seem to show a continuous behavior. Then, the

macroscopic density (ρ) and velocity (~u) are calcu-

lated from the respective moments of the density dis-

tribution, as follows:

ρ(~x,t) =

∑

i=0

(~x,t), (6)

~u(~x,t) =

ρ(~x,t)

∑

i=0

(~x,t)~c

. (7)

To compute the evolution of the simulation it is

need to deﬁne an initial conﬁguration for the LBM

nodes such as the boundary condition. The initial con-

dition is deﬁned for all the LBM nodes using the equi-

librium function given by expression (5). To do so, it

is necessary to set an initial value for the macroscopic

quantities (density and velocity). As will be explained

in section 6, the proposal of this work is to use a ve-

locity ﬁeld computed by GVF as initial condition to

LBM.

Different types of boundaries have been intro-

duced in the ﬁeld of hydrodynamics for the LBM.

Bounce-back is the simplest one, where boundary

nodes are placed halfway between the lattice nodes.

When the particles propagate to the boundary nodes,

they just bounce back along the direction they came

from. Due to its simplicity, this method does not

properly determine the velocity and density value for

these boundary nodes. An incorrect density or veloc-

ity value at the boundary nodes can eventually cause a

negative density value at local lattice points, and this

error can then accumulate along the simulation.

We implemented the boundary conditions based

on the work of (Zou and He, 1997), where the authors

proposed a way to specify density or velocity at the

boundary nodes, based on the idea of bounce-back of

the nonequilibrium distribution. To do so, we had to

take care of two kinds of boundary conditions: the

nodes that lie in the wall and the nodes that lie in the

corner of the lattice. In this approach, the boundary is

part of the simulation domain and a regular collision

is applied on boundary nodes.

4 THE GVF METHODOLOGY

The Gradient Vector Flow (GVF) ﬁeld is deﬁned as

the vector ﬁeld v(x, y) = (u(x,y),v(x,y)) that mini-

mizes the energy functional:

ε =

Z Z

[µ(u

+ u

+ v

) + |F|

|v − F|

]dxdy

(8)

where F = (F

(x,y),F

(x,y)) is a ﬁeld deﬁned over

the domain of interest. When F is small, the energy

is dominated by partial derivatives of the vector ﬁeld,

yielding a smooth ﬁeld. Otherwise, the second term

dominates the integrand, and is minimized by setting

v = F. The parameter µ is a regularization parameter

that should be set according to degree of smoothness

required.

The GVF can be found by solving the associated

Euler-Lagrange equations given by:

µ∇

u − (u − F

)(F

+ F

) = 0 (9)

µ∇

v − (v − F

)(F

+ F

) = 0 (10)

where ∇

is the Laplacian operator. Equations (9) and

(10) can be solved by treating u and v as functions of

time t and solving:

(x,y,t) = µ∇

u(x,y,t) − (u(x, y,t) − F

(x,y))

·(F

+ F

) (11)

(x,y,t) = µ∇

v(x,y,t) − (v(x, y,t) − F

(x,y))

·(F

+ F

) (12)

subject to some initial condition v(x, y,0) = v

(x,y).

The steady-state solution (as t → ∞) of these parabolic

equations is the desired solution of the Euler-

Lagrange equations (9) and (10). These are reaction-

diffusion equations and are known to arise in areas

as heat conduction, reactor physics, and ﬂuid ﬂow.

The ﬁeld obtained by solving the above equation is

a smooth and extended version of the original one.

5 SKETCH-BASED MODELING

The Sketch-Based Modeling (SBM) is a computa-

tional research area that focus on intuitive simpliﬁed

modeling techniques. It is based on the sketch process

made by traditional artist. Basically, the sketch-based

modeling program has to provide a comfortable and

intuitive environment where the artist can freely draw

his object. Then, using the sketch as an input, the pro-

gram must interpret the data and ﬁnd an approximate

representation (Cook and Agah, 2009).

SKETCHING FLUID FLOWS - Combining Sketch-based Techniques and Gradient Vector Flow for Lattice-Boltzmann

Initialization

331

The sketch process starts with the drawing done

by the user through some input device (for example,

mouse, tablet or touch screen). This drawing is then

sampled and stored with some information such as

position, velocity, pressure, among others. The type

of information that can be stored depends on the de-

vice being used. For example, some devices provide

pressure information, multiple touches or slope of the

pen. Another device-dependent aspect is the sam-

ple frequency, which determines the sample distribu-

tion (Cruz and Velho, 2010).

The goal of a sketch-based modeling program is

to model the object intended by the user, not neces-

sarily what was drawn on the input device. One issue

with this type of system occurs when the user does

not have much ability to design or handling the de-

vice. In this case, the tracing performed may be in-

accurate. Another common issue is the noise from

the device, which comes from an inaccurate drawing

capture. Due to the presence of noise, it is common

to perform a ﬁltering of sampled data. Another fea-

ture is to perform a ﬁtting of the data for a convenient

curve (Cruz and Velho, 2010).

The data are stored as a sequence of points, T =

,..., p

}, where n is the number of samples and

= (x

) indicates the position (x

) and in-

stant t

each point was sampled. If the data acquisi-

tion device captures more information, the point can

be thought of as (x

,..., x

), where each element rep-

resents an attribute of the point. Besides the attributes

captured, it is also possible to calculate a few others,

such as velocity and acceleration. All this information

can be useful to add features to the model.

The points are conveniently grouped together to

build a two-dimensional model to which the system

must infer some meaning. This model is called the

sketch. The sketch can be used both for creating and

editing of 3D graphic object being modeled, such as

to control. In the latter case the application decides

which task to perform, according to the interpreta-

tion of the sketch. This is known as sketch of ges-

ture (Thorne et al., 2004).

6 PROPOSED METHOD

For modeling a ﬂuid through LBM we need to dis-

cretize the domain, set the initial and boundary con-

ditions and then to apply the local rule of evolu-

tion. However, in the ﬁeld of animation, it is com-

mon to generate scenes from advanced states of ﬂuid

dynamics generated through ﬂuid simulation tech-

niques. The initialization of the simulation is a fun-

damental step.

The main goal of this work is primarily concerned

with how to take drawing input from the user and con-

vert it into an initial ﬂuid conﬁguration. We claim

that such task can be implemented through an intu-

itive framework for ﬂuid modeling using sketching

techniques and GVF. From the viewpoint of computer

graphics applications we need an efﬁcient way to get

user actions, convert then into a model and to visual-

ize the model simulation.

In the case of ﬂuid dynamics the sketching of the

initial conﬁguration is much more complex because

there are too many degrees of freedom to consider.

However, in terms of high level features, the initializa-

tion of the LBM simulation can be performed through

the initial velocity ﬁeld and convenient boundary con-

ditions that deﬁne the ﬂuid behavior nearby the fron-

tiers of the domain.

In this work the main focus is a sketch based

framework to deﬁne the initial velocity ﬁeld of the

ﬂuid. In this way, streamlines are very intuitive ﬂuid

features that can be mathematically deﬁned by the ini-

tial value problem:

= v(x), x(0) = P

, (13)

where v, is the velocity ﬁeld. The solution of this

problem for a set of initial conditions gives a set of

(integral) curves which can be interpreted as the tra-

jectory of massless particles upon the ﬂow deﬁned by

the velocity ﬁeld.

Obviously the application of the mathematical

deﬁnition above only works if we know the veloc-

ity ﬁeld which is exactly the target of our framework.

However, the streamline concept can be used as a

guide in the process of taking input drawings from the

user and to convert them into a model. Speciﬁcally,

once deﬁned the boundaries of the ﬂuid domain, the

user must draw a set of paths by moving the mouse

cursor that the system translates as streamlines. So,

the tangent ﬁeld over these paths will be used to set

up the GVF computation in order to get the initial ve-

locity ﬁeld.

The user paths are translated as streamlines of

the ﬂuid and the corresponding tangent vector ﬁeld

is computed. The tangent ﬁeld computation can be

performed by ﬁtting a spline model to each user path

or simply by taking a sequence of points p

,..., p

over the path and computing the vectors v

= α

− p

i−1

), i = 2, 3, ..., k, where α

is a scale factor

speciﬁed by the user in order to control the veloc-

ity ﬁeld intensity over the streamline. A smoothed

version of the tangent ﬁeld over these paths (convo-

lution with a Gaussian kernel) gives the ﬁeld F =

(x,y),F

(x,y)) in expressions (11)-(12) and the

initial condition v

of the GVF.

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

332

Then, the solution of GVF equations generates the

initial velocity ﬁeld that we need to set up the LBM

simulation through the equilibrium function given by

expression (5).

To implement this idea, we shall provide an user

interface that allows free interaction for the user, as

we can see in Figure 2. In this ﬁgure we show a draw-

ing canvas aligned with the computer screen which

is used to deﬁne the ﬂuid domain. The + and - but-

tons allow the user to change the domain resolution.

The SKETCH button makes possible for the user to

freely draw the sketching over the domain, using the

mouse. The HOLES button allows setting hole re-

gions into the ﬂuid domain, which shall not be af-

fected by the ﬂuid simulation model. The GVF button

takes the collection of points given by the sketch and

then compute the tangent ﬁeld. After that, the tangent

ﬁeld is used as input to the GVF method, which ﬁ-

nally gives the initial velocity ﬁeld that will be used as

input to the LBM. Finally, the RUN and RESET but-

tons control the simulation. The framework was de-

veloped using the C/C++ programming language with

the OpenGL library for the visualization.

For example, Figure 3(a) illustrates a sketching

made by the user in a 100 × 100 grid, with a hole in-

side the canvas deﬁning a multiply connected domain.

The interface must interpret the user’s input and trans-

lates all the information to a ﬂuid simulation model,

which shall recreate a visual state constrained to the

sketch. In this way, Figure 3(b) shows the tangent

ﬁeld calculated along the sketching path, Figure 3(c)

Figure 2: The graphical user interface of the proposed

framework.

Figure 3: (a) Example of sketching made by the user. (b)

The tangent ﬁeld. (c) The initial velocity ﬁeld given by the

GVF. (d) The LBM initialization through the ﬁeld in (c).

shows the velocity ﬁeld given by the GVF using as in-

put the tangent ﬁeld and respecting the multiply con-

nected domain. Finally, Figure 3(d) shows the initial-

ization of the LBM using the GVF as initial condition.

Such framework can be applied for 3D simula-

tions because all its basic components (GVF, LBM,

streamlines) are applied for three dimensional ﬁelds

without extra machinery.

7 RESULTS

In section 6 we explained our proposal for combining

sketch-based techniques and Gradient Vector Flow

for Lattice-Boltzmann initialization. This sections

presents some examples of ﬂuid ﬂows achieved by

our framework. For the results explained below the

dimension of the grid is 100 × 100.

The LBM initialization is given by the equilibrium

function deﬁned in expression (5), which depends on

the macroscopic quantities density and velocity. The

initial macroscopic velocity ﬁeld is given by the GVF

method. The initial macroscopic density ﬁeld is de-

ﬁned as ρ = 1.0. The experiments were performed

with an Intel Core 2 Quad 3.0 GHz, with 4 GB of

RAM and a Video Card NVidia GeForce 9800 GTX,

running Windows XP. The pictures in this article were

obtained through the implemented framework.

The ﬁrst example deﬁnes a horizontal ﬂow from

SKETCHING FLUID FLOWS - Combining Sketch-based Techniques and Gradient Vector Flow for Lattice-Boltzmann

Initialization

333

Figure 4: Example 1: horizontal ﬂow from left to right with

a hole. (a) The sketching. (b) The tangent ﬁeld. (c) The

initial velocity ﬁeld given by the GVF. (d) The LBM initial-

ization through the ﬁeld in (c).

left to right, with a hole in the domain. This exam-

ple shows a traditional 2D simulation of a ﬂow past a

cylinder.

Figure 4(a) shows the sketching made by the user.

In Figure 4(b) we can see the tangent ﬁeld calculated

through the sketching information. Once we have the

tangent ﬁeld, the application is able to calculate the

GVF, shown in Figure 4(c).

Finally, the LBM is initialized using the GVF in-

formation as input, shown in Figure 4(d). In this case,

we expect some symmetry for the ﬁelds due to the

physics and geometry behind the ﬂuid evolution. In

fact, we observe this property in the GVF result. The

Figure 5(a)-(d) illustrates four instants of the LBM

simulation for this example.

The next example illustrates a ﬂow that happens

in the animation of a gas jet interacting with a solid

object. The sketching for this case is just a straight

line as shown in Figure 6(a). In Figure 6(b) we can

see the tangent ﬁeld calculated through the sketching

information.

Once we have the tangent ﬁeld, the application is

able to calculate the gradient vector ﬂow, shown in

Figure 6(c). Finally, the LBM is initialized using the

GVF information as input, shown in Figure 6(d). We

can observe that the result of the gradient vector ﬂow

gives the main stream of the jet, which is picture on

Figure 6(c).

After computing all these initial ﬁelds, we now

Figure 5: Example 1: the evolution of the ﬂuid simulation.

The sequence (a)-(d) shows four instants of the LBM sim-

ulation, which was initialized using Figure 4(d) as initial

velocity condition.

are able to simulate the ﬂuid which shall respect

our sketching. Figure 7(a)-(d) illustrates four in-

stants of the evolution of the ﬂuid simulation through

LBM. We can observe that the LBM simulation can

reproduce the expected vortices in the surrounding

medium.

In the above examples the obstacles within the

ﬂuid domain are ﬁxed regions, where the velocity

ﬁeld must be null. This is done automatically by

the system, through the mapping of the corresponding

LBM nodes. All these nodes are deﬁned as a bound-

ary node.

Finally, the following example explores also the

ﬂow past a cylinder starting from a sketching that is

a simpliﬁcation of the ﬂow shown in Figure 8. The

source of this ﬁgure is the work of (Schroeder et al.,

2010), which presents a sketch-based system to cre-

ate illustrative visualizations of 2D vector ﬁelds. This

ﬁgure pictures the illustrative visualizations of a snap-

shot of the ﬂow when setting the Reynolds number to

100.

Our ﬁnal example tries to simulate this behavior

through a simpliﬁed sketching. The Figure 9 pictures

a sketch of that ﬂow representing a simpliﬁed version

of it, done through our framework. The Figure 10

shows the evolution of the simulation. We can ob-

serve that through a simpliﬁed sketching it is possible

to achieve approximate behaviors of complex ﬂows.

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

334

Figure 6: Example 2: ﬂow of a gas with a solid object. (a)

The sketching. (b) The tangent ﬁeld. (c) The initial velocity

ﬁeld given by the GVF. (d) The LBM initialization through

the ﬁeld in (c).

Figure 7: Example 2: the evolution of the ﬂuid simulation.

The sequence (a)-(d) shows four instants of the LBM sim-

ulation, which was initialized using Figure 6(d) as initial

velocity condition.

8 CONCLUSIONS

In this work we presented a sketch-based system that

allows an intuitive ﬂuid ﬂow initialization for com-

Figure 8: An illustrative ﬂow past a cylinder with Reynolds

number 100. (Source: (Schroeder et al., 2010))

Figure 9: A simpliﬁed version of the Figure 8.

puter graphics applications. We proposed a combina-

tion of sketching techniques with the Gradient Vec-

tor Flow method to obtain a smooth initialization for

the simulation. The ﬂuid simulation is done using a

two-dimensional Lattice Boltzmann Method (LBM).

With the sketching techniques the system enables the

user to draw freely the initial state of the ﬂuid ﬂow

using an intuitive interface. The results section illus-

trates some classical examples of ﬂuid ﬂow simulated

through our system. We observed that it was able to

simulate some complex ﬂows through simple initial

drawing.

A future direction for this work is to improve the

drawing process. Expected symmetries compose also

other point that our proposal must consider. For ex-

ample, in the 2D simulation of a ﬂow past a cylinder

the animator is free to sketch a conﬁguration which

does not have the symmetry observed in Navier-

Stokes simulations of incompressible ﬂows with no-

slip boundary conditions. Our system must check

such problem and warn the user or automatically ﬁx

it. The user is free to place the streamlines in any con-

ﬁguration he has in mind. But, the user may sketch

SKETCHING FLUID FLOWS - Combining Sketch-based Techniques and Gradient Vector Flow for Lattice-Boltzmann

Initialization

335

Figure 10: Example 3: the evolution of the ﬂuid simulation.

unstable conﬁgurations that changes too fast without

adding extra machinery to the ﬂuid ﬂow model. This

may be an undesirable behavior depending on the an-

imator goals. Moreover, we want to combine image

processing techniques, so that we can use as input

some photos of ﬂuid ﬂows and extract from them a

potencial initial velocity ﬁeld for the GVF method.

Another future direction of the proposed work is

to extend the two-dimensional approach to a three-

dimensional one. Such framework can be applied

for 3D simulations because all its basic compo-

nents (GVF, LBM, streamlines) are applied for three-

dimensional ﬁelds without extra machinery.

REFERENCES

Aubert, G. and Kornprobst, P. (2002). Mathematical Prob-

lems in Image Processing: Partial Differential Equa-

tions and the Calculus of Variations. Springer-Verlag,

New York.

Bærentzen, J. A. and Christensen, N. J. (2002). Volume

sculpting using the level-set method. In Proceedings

of the Shape Modeling International 2002 (SMI’02),

pages 175–, Washington, DC, USA. IEEE Computer

Society.

Buick, J. M., Easson, W. J., and Greated, C. A. (1998). Nu-

merical simulation of internal gravity waves using a

lattice gas model. International Journal for Numeri-

cal Methods in Fluids, 26(6):657–676.

Chen, S. and Doolen, G. D. (1998). Lattice boltzmann

method for ﬂuid ﬂows. Annual Review of Fluid Me-

chanics, 30:329–364.

Chopard, B., Luthi, P., and Masselot, A. (1998). Cellular

automata and lattice boltzmann techniques: An ap-

proach to model and simulate complex systems. In

Advances in Physics.

Cook, M. T. and Agah, A. (2009). A survey of sketch-based

3-d modeling techniques. Interact. Comput., 21:201–

211.

Cruz, L. and Velho, L. (2010). A sketch on sketch-based in-

terfaces and modeling. In Graphics, Patterns and Im-

ages Tutorials (SIBGRAPI-T), 2010 23rd SIBGRAPI

Conference on, pages 22 –33.

Foster, N. and Metaxas, D. (1997). Modeling the motion of

a hot, turbulent gas. In SIGGRAPH, pages 181–188.

ACM.

Higuera, F. J., Jimenez, J., and Succi, S. (1989). Boltzmann

approach to lattice gas simulations. Europhys. Lett.,

Igarashi, T., Matsuoka, S., and Tanaka, H. (2007). Teddy: a

sketching interface for 3d freeform design. In ACM

SIGGRAPH 2007 courses, SIGGRAPH ’07, New

York, NY, USA. ACM.

McNamara, G. R. and Zanetti, G. (1988). Use of the boltz-

mann equation to simulate lattice-gas automata. Phys.

Rev. Lett., 61(20):2332–2335.

uller, M., Keiser, R., Nealen, A., Pauly, M., Gross, M.,

and Alexa, M. (2004a). Point based animation of

elastic, plastic and melting objects. In ACM SIG-

GRAPH/Eurographics symposium on Computer ani-

mation, pages 141–151. Eurographics Association.

uller, M., Schirm, S., and Teschner, M. (2004b). Inter-

active blood simulation for virtual surgery based on

smoothed particle hydrodynamics. Technol. Health

Care, 12(1):25–31.

Rothman, D. H. and Zaleski, S. (1994). Lattice-gas mod-

els of phase separation: Interface, phase transition and

multiphase ﬂows. Rev. Mod. Phys, 66:1417–1479.

Schroeder, D., Coffey, D., and Keefe, D. (2010). Draw-

ing with the ﬂow: a sketch-based interface for illustra-

tive visualization of 2d vector ﬁelds. In Proceedings

of the Seventh Sketch-Based Interfaces and Modeling

Symposium, SBIM ’10, pages 49–56, Aire-la-Ville,

Switzerland, Switzerland. Eurographics Association.

Stam, J. (2003). Flows on surfaces of arbitrary topology. In

SIGGRAPH, pages 724–731. ACM.

Sutherland, I. E. (1964). Sketchpad - a man-machine graph-

ical communication system. In Proceedings of the

SHARE design automation workshop, DAC ’64, pages

6.329–6.346, New York, NY, USA. ACM.

Thorne, M., Burke, D., and van de Panne, M. (2004). Mo-

tion doodles: an interface for sketching character mo-

tion. ACM Trans. Graph., 23:424–431.

Varley, P. A. C., Martin, R. R., and Suzuki, H. (2004). Can

machines interpret line drawings? EUROGRAPHICS

Workshop on Sketch-Based Interfaces and Modeling.

Wei, X., Member, S., Li, W., Mueller, K., and Kaufman,

A. E. (2004). The lattice-boltzmann method for sim-

ulating gaseous phenomena. IEEE Transactions on

Visualization and Computer Graphics, 10:164–176.

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

336

Williams, L. (1990). 3d paint. SIGGRAPH Comput. Graph.,

24:225–233.

Witting, P. (1999). Computational ﬂuid dynamics in a tra-

ditional animation enviroment. In SIGGRAPH, pages

129–136. ACM.

Xu, C. and Prince, J. L. (1997). Gradient vector ﬂow: A

new external force for snakes. In IEEE Proc. Conf.

On, pages 66–71.

Xu, C. and Prince, J. L. (1998). Snakes, shapes, and gradi-

ent vector ﬂow. IEEE TRANSACTIONS ON IMAGE

PROCESSING, 7(3):359–369.

Zeleznik, R. C., Herndon, K. P., and Hughes, J. F. (2006).

Sketch: an interface for sketching 3d scenes. In ACM

SIGGRAPH 2006 Courses, SIGGRAPH ’06, New

York, NY, USA. ACM.

Zhu, B., Iwata, M., Haraguchi, R., Ashihara, T., Umetani,

N., Igarashi, T., and Nakazawa, K. (2011). Sketch-

based dynamic illustration of ﬂuid systems. In SIG-

GRAPH ASIA 2011 Technical Papers, Hong Kong.

Zou, Q. and He, X. (1997). On pressure and velocity bound-

ary conditions for the lattice boltzmann bgk model.

Physics of Fluids, 9(6):1591–1598.

SKETCHING FLUID FLOWS - Combining Sketch-based Techniques and Gradient Vector Flow for Lattice-Boltzmann

Initialization

337