GRAPH BASED DESCRIPTOR EVALUATION TOWARDS

AUTOMATIC FEATURE SELECTION

Anita Keszler, Levente Kov´acs and Tam´as Szir´anyi

Distributed Events Analysis Research Group,

Computer and Automation Research Institute of the Hungarian Academy of Sciences (MTA SZTAKI), Budapest, Hungary

Keywords:

Graph Representation, Components, Feature Selection.

Abstract:

This paper presents the ﬁrst steps towards an automated image and video feature descriptor evaluation frame-

work, based on several points of view. First, evaluation of distance distributions of images and videos for

several descriptors are performed, then a graph-based representation of database contents and evaluation of

the appearance of the giant component is performed. The goal is to lay the foundations for an evaluation frame-

work where different descriptors and their combinations can be analyzed, with the goal of later application for

automatic feature selection.

1 INTRODUCTION

Recent multimedia databases require large amounts

of memory and computing power for storage and pro-

cessing, and there is a need to efﬁciently index, store,

and retrieve the embedded information.

Usual methods in dimensionality reduction in-

volve various areas including Principal Component

Analysis, clustering methods, neighbour searching al-

gorithms, and so on. One of the recent approaches in-

volvesgraph based clustering and componentanalysis

methods. The generic questions and open issues here

remain how to build the graphs (regarding selection of

edges and weights), and how to navigate the graphs

efﬁciently (i.e. neighbourhood searching). Numer-

ous graph based methods have been published in the

area of image/video clustering and retrieval. How-

ever, there are still several open questions in image

processing and graph theory as well. Among several

other problems, one of the most important step is to

select the proper descriptors.

Feature selection algorithms typically can be cat-

egorized into feature ranking (based on a metric) and

subset selection (optimal set of features) methods.

The most common selection techniques are some sort

of subset selection (e.g. wrappers). In this case the

high dimensionality can be considered. In (Chapelle

et al., 2002) a SVM based feature selection method is

applied where the scaling factors are adjusted using

the gradient of a theoretical upper bound on the error

rate.

We propose and work towards practically proving

that graph theoretic approaches can be useful in de-

scriptor selection as well. As others have also begun

to investigate, we build our approach on the investi-

gation of image/video distance distributions accord-

ing to several descriptors and analysing their relation

and behaviour w.r.t. component formulation and giant

component appearances.

In (Zhang et al., 2010) a query by example ap-

proach where histograms of point distances are in-

vestigated for 2 vs 100 feature dimensions for low

number of vertices (250), as a basis to show that

with increased dimensions the distance distribution of

points tend to be narrower (distances decrease, show-

ing poorer discrimination). An approach for feature

selection in the presence of irrelevant features (noise)

is introduced in (Sun et al., 2010), taking into con-

sideration of sample datapoints in 2D space for de-

cision boundary selection and investigating the dis-

tribution of feature weights in high dimensions. An-

other method (Morris and Kender, 2009) is based on

an approx. 1000 features on real videos, using a

heuristic algorithm for feature retention, and using

the sort-merge approach for selecting ranked feature

groups. A method for sports video feature selection

is presented in (Shen et al., 2007) using Mean Shift

clustering based on motion signatures and colour fea-

tures. Setia et al. (Setia and Burkhardt, 2006) present

a method for automatic image annotation by a fea-

ture weighting scheme and SVM using a combina-

tion of colour, texture and edge features.Guldogan et

al. (Guldogan and Gabbouj, 2008) present an auto-

matic feature selection approach for ﬁnding features

375

Keszler A., Kovács L. and Szirányi T..

GRAPH BASED DESCRIPTOR EVALUATION TOWARDS AUTOMATIC FEATURE SELECTION.

DOI: 10.5220/0003868503750380

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 375-380

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

that best describe a speciﬁc dataset investigating mu-

tual information and principal component analysis.

Conversely to other approaches, in our case we do

not use artiﬁcial weighting of features and distances

or a priori clustering or machine learning steps, but

instead use real data with multiple features and weigh

the built distance graphs by the points’ differences ac-

cording to a speciﬁc feature, and investigate the be-

haviour of the difference distributions. We investi-

gate the possible connections between distance dis-

tribution histograms and the appearance of the giant

component in random geometric graphs, which are

the closest representation of point vs. difference (i.e.

distance) behaviour in real life datasets. The goal is to

show that the method of difference distribution anal-

ysis is a good alternative to previous methods to ﬁnd

features with higher discrimination. We intend to lay

the foundations of a framework for automatic feature

evaluation and selection based solely on the descriptor

difference statistics and the respective graph analysis

with the goal of ﬁnding the best possible selection of

descriptor combinations for the representation of re-

lated image and video contents.

2 DESCRIPTOR EVALUATIONS

FOR FEATURE SELECTION

2.1 Dataset

The dataset used for the performed tests was a video

database collected from real television captures, re-

sized to 320 pixel width. The captures consist of var-

ious content categories, e.g. sport , nature , cartoons,

news, street surveillance, outdoor, indoor, also con-

taining various types of camera motions, shot lengths,

and scene contents. Some example frames from vari-

ous videos are shown on Fig. 1. The videos were cut

into shots by our automatic shot detector, resulting in

6900 video shots with various length. The total time

length of the dataset videos is 515.82 minutes.

Figure 1: Sample frames from a small subset of different

video contents.

For each shot a representativeframe was extracted

(based on colour histograms). When running image-

based descriptors, these representative frames are

used as the input for a shot. When running shot/video-

based descriptors, the entire shot is used as an input.

For this dataset, we extracted all the features for im-

ages and video segments, and we also calculated the

distances of each element from all the others (thus en-

abling the creating of fully connected distance graphs

based on the extracted features).

2.2 Descriptors and Distance Measures

With the intent of evaluating various features for

general distribution and content differentiation, we

selected a set of descriptors. Some are standard

MPEG-7 descriptors (Manjunath et al., 2001), but we

also use other features as well: local binary patterns

(LBP) (Ojala and Pietikainen, 2002), curvelets (Can-

des et al., 2006), colour segmentation (Mean-Shift

(Comaniciu and Meer, 2002) based). Further fea-

tures were developed by us (average colour, relative

focus regions (Kov´acs and Szir´anyi, 2007), average

motion).

For calculating the differences between im-

ages/videos, we need to take into consideration which

types of information the extracted features contain.

For each descriptor, we used an Euclidean distance

metric, i.e. for a feature all elements can be displayed

along a 1D axis from 0 to d

max

(D) (maximal differ-

ence for the descriptor) and they all adhere to the tri-

angle inequality.

In the following we list the feature contents and

the used distance calculations for the used descriptors:

• MPEG-7 features: see (Manjunath et al., 2001)

for a comprehensive description of the extracted

feature and the used metrics.

• LBP and curvelets: Euclidean distance.

• Average colour: calculates the average colour for

image blocks and produces a quantized histogram

of such colours. Colour segmentation: calcu-

lates an image where different region classes are

colour coded and a quantized histogram is pro-

duced; the difference between two quantized his-

tograms in both cases is calculated as the sum

of absolute differences (SAD) of the 2 normal-

ized histograms: d(h

) = SAD(h

1,N

,h2

1,N

) =

∑

4096

i=0

1,N

(i) − h

2,N

(i)| where

1,N

(i) =

(i) − h

1,min

1,max

− h

1,min

(1)

and similarly for h

2,N

• Relative focus regions: blurred/focusedregion ex-

traction based on (Kov´acs and Szir´anyi, 2007);

produces a relative focus map; the difference be-

tween two focus maps is the sum of squared dif-

ferences: SSD( f

, f

) =

fw∗ fh

∑

fw∗ fh

i=0

( f

(i) −

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

376

(i))

where fw, f h are the width and height of

the maps.

• Average motion: calculates the average motion

direction for frame blocks and produces a direc-

tion histogram for the video segment on which

it was run; the differences are calculated as the

root squared difference of the two histograms:

d(h

∑

1,i

− h

2,i

)

3 DISTRIBUTIONS OF PAIRWISE

DISTANCES

The graph of elements is built as follows. The vertex

set of the graph models the images/videos, the dis-

tance between them is calculated using the extracted

features. The edge weights of the graph are propor-

tional to the distances. The distribution of the result-

ing distance values is then analysed. The test results

show that depending on the descriptor used to calcu-

late the distances, the distance distributions can differ

in important aspects, which we intend to exploit.

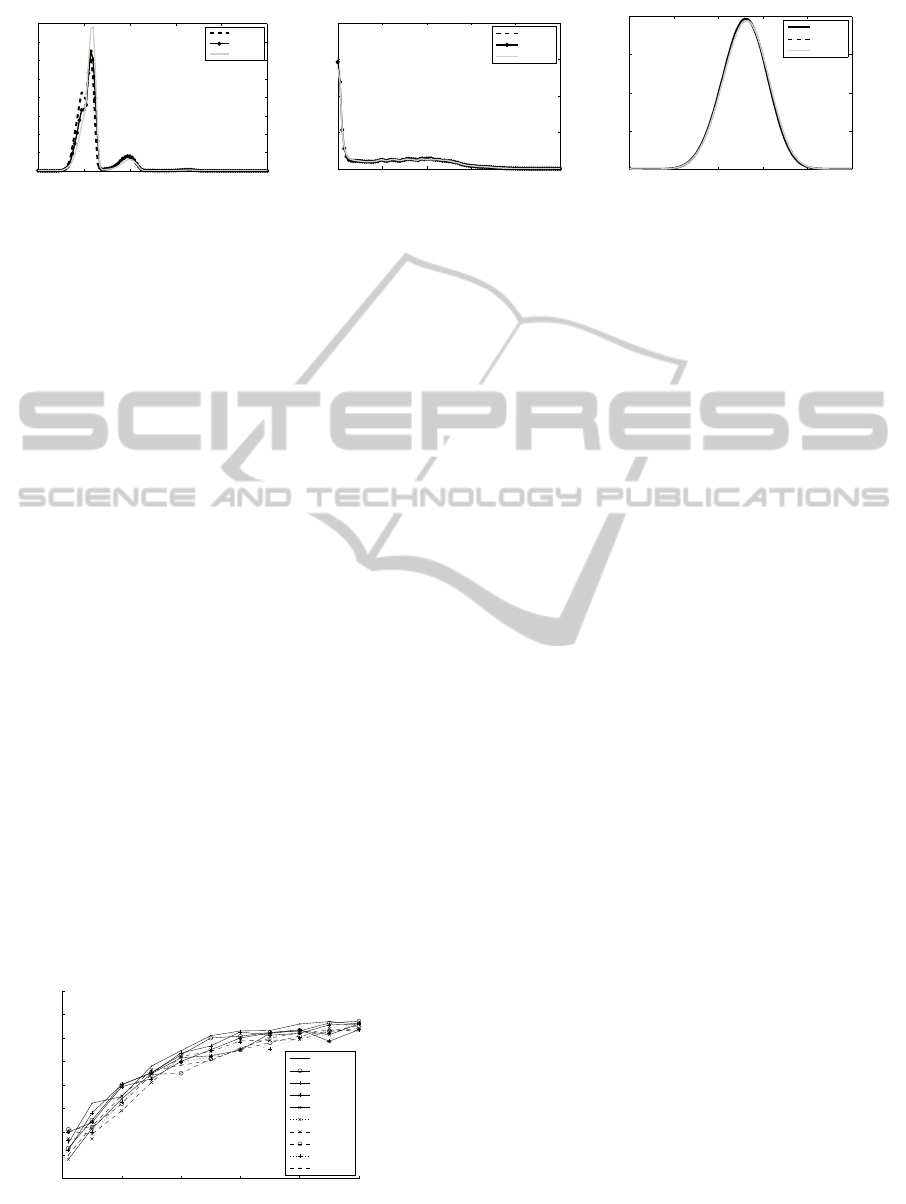
The investigation of distance distributions among

database elements according to different descriptors

provides information about the discriminative proper-

ties of a certain descriptor (Fig. 2 shows some exam-

ples of such distributions). As others (Zhang et al.,

2010) have shown for small point sets, difference dis-

tribution behaviour can be a basis for descriptor se-

lection (or dropping). In our case, we produced dis-

tance distributions for approx. 7000 elements from

the database, applying 13 different descriptors (cal-

culating the distance of each image/video from each

other, for all descriptors). Our empirical results show

that descriptors which produce distance histograms

with the main peak near 0 will be less discriminative

than others (i.e. most of the elements gather in one

group).

4 GIANT COMPONENTS AND

PHASE TRANSITION IN

RANDOM NETWORKS

The appearance of the giant component is a well

known phenomenon and it was investigated in several

papers, but mostly in random networks. The results

known in this topic correspond to theoretical results

on the existenceof the giant component, and measure-

ments on the exact threshold where the giant compo-

nent ﬁrst appears. Applications are usually restricted

to the ER-model, however in recent years random ge-

ometric graphs (RGG) have received more attention.

These type of graphs have the ability to model net-

works, where the edge weights are not independent,

for example derived from a metric between the ver-

tices, and this model stands closer to modelling real

image/video datasets. In this section we will give a

short overview on the problem of the giant compo-

nent, the random graph models, and the known re-

sults.

4.1 ER-model

Erdos and Renyi analysed the properties of a random

graph with uniformly distributed edges (Erdos and

Renyi, 1960). They considered the evolution of the

components, while adding randomly selected edges

to the graph. The process starts with n vertices and 0

edges, and in each step a randomly selected new edge

is added independently of the already chosen edges.

Recent results connected to this problem are formu-

lated using the number of vertices, and the p probabil-

ity of the existence of an edge (G(n, p)). p is usually

described as a function of a parameter c: p = c/n.

Part of the theorem of Erdos and Renyi presented

in (Erdos and Renyi, 1960) can be formulated as fol-

lows:

Theorem 1. (Erdos-Renyi) The behaviour of the ER-

graph from the point of view of component sizes can

be divided into three important phases: The size of

the largest component is denoted by C

max

1) c < 1: C

max

= O(lnn). (The graph has small

components)

2) c = 1: C

max

= Θ(n

2/3

3) c > 1: C

max

= O(n) (giant component), but all

the other components have size O(lnn).

The results presented in (Erdos and Renyi, 1960)

also deal with the complexity of the components, but

now we only interested in their size.

4.2 Random Geometric Graphs

Besides the above mentioned classic random graph

models, several different versions have been pub-

lished in order to model certain properties of complex

real networks. For example in case of distance graphs,

the edge-weights corresponds to pairwise distances of

objects based on a given metric. Random geometric

graph models offer a solution to mimic these type of

dependencies, since in this model, the edge-weights

are not selected independently of each other (Penrose,

2003).

Deﬁnition 1. A random geometric graph or RGG is

obtained as follows. We take X

,...,X

∈ R at ran-

dom (according to some probability distribution ν on

GRAPH BASED DESCRIPTOR EVALUATION TOWARDS AUTOMATIC FEATURE SELECTION

377

0 0.2 0.4 0.6 0.8 1

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

Edgeweights

Ratio of appearance

N=4000

N=5000

N=6899

(a) Average colour based distance distributions

0 0.2 0.4 0.6 0.8 1

0.05

0.1

0.15

0.2

Edgeweights

Ratio of appearance

N=4000

N=5000

N=6899

(b) Focus histogram based distance distributions

0 0.2 0.4 0.6 0.8 1

0.01

0.02

0.03

0.04

Edgeweights

Ratio of appearance

Random samples − uniform, 10 dimensions

N=4000

N=5000

N=7000

Figure 2: Distance distribution histograms for different descriptors.

, where d is the number of dimensions). For i 6= j

we connect X

and X

if k X

− X

k< r

. r

is the ra-

dius of the random geometric graph.

The existence of the giant component in random

geometric graphs has also been examined. Thermod-

inamic limit, a term of statistical physics was used to

describe this phenomenon. This limit corresponds to

the critical radius of the RGG: r

∼ c· n

−1/d

. At this

limit, the expected value of the average degree in the

graph tends to a constant. Above a certain c constant

in the formula of the radius r

there is likely to be a

giant component.

Unfortunately, the exact value of r

is unknown.

The fact, that 0 < r

< ∞, if d ≥ 2 is an interesting

result of continuum percolation, in itself.

Our aim with the tests on random geometric

graphs is to analyse the correspondence between the

critical value r

(or in other words the critical edge

weight), the dimension of the RGG and the number

of vertices. Although we cannot give exact values,

the tendencies are also important in real applications,

and for our purposes.

In Fig. 3 the correspondence between the previ-

ously mentioned parameters is shown. It is important

to note, that the number of dimensions has a signif-

icant impact on the critical edge weight in case of

RGGs. There is a difference between the results in

case of different graph sizes as well, but it is not that

relevant compared to the number of dimensions.

0 20 40 60 80 100

0.55

0.6

0.65

0.7

0.75

0.8

0.85

0.9

0.95

Number of dimensions

Weight thresholds

Critical weight values

N=1000

N=2000

N=3000

N=4000

N=5000

N=6000

N=7000

N=8000

N=9000

N=10000

Figure 3: Critical weight values of artiﬁcial datasets.

5 GIANT COMPONENTS IN

REAL DATASETS

The appearance of the giant component in real net-

works with geometric restrictions on the edge weights

is an interesting mathematical topic on its own, but it

also has the potential to be used in applications where

the structure of the evolving graph is important as

well.

In retrieval and clustering tasks ﬁnding the ’op-

timal’ graph structure is still an open question. Al-

gorithms for weighted graphs are usually more com-

plex than the ones for non-weighted graphs. Due to

this fact, several applications transform the originally

weighted graph into a non-weighted one for process-

ing. In this case the question arises: how to transform

the weighted graph? The generally applied solution is

to select a distance threshold; if the distance between

two vertices is lower than the threshold, the vertex

pair will be connected. Studying the graph structure

with differentthresholds is a key step for selecting this

threshold.

On one hand, our tests intent to analyse the evolv-

ing components at different thresholds for a given de-

scriptor and the corresponding metric. On the other

hand, graphs of different descriptors are compared,

and based on the these test results, we propose a new

aspect of comparing the descriptors themselves.

5.1 Appearance of the Giant

Component

The ’descriptor graphs’ were analysed to ﬁnd out

whether the appearance of the giant component is

traceable, and if it is, how does it depend on the se-

lected descriptor. By deﬁnition, the giant component

is a component with size O(n), while all other compo-

nents have size O(logn), so the exact critical threshold

can be determined by the analysis of the asymptotic

behaviour of the network. In the case of our tests on

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

378

Figure 4: Example of components at an inner building step of the Edge histogram graph. The similar images tend to corre-

spond in the same component.

real data this type of test can not be carried out, since

we are working with a ﬁnite number of vertices, but

acceptable estimations are available.

The stopping condition for selecting edges in the

descriptor graph is the estimated threshold, where the

giant componentappears. In our ﬁnite graphsthe ratio

of the second and the largest component will be the

parameter to track the evolving components.

5.2 Ratios of Largest and Second

Largest Components

The ratio of the largest and second largest component

is relevant with relation to descriptor behaviour, dur-

ing the building of the graph in the search for the point

where the single giant component appears. This ratio

shows different behaviour w.r.t. simulated datasets,

showing multiple peak regions during the process.

This means, that during the graph edge/weight se-

lection there are intervals when multiple components

grow in parallel, which is inline with the expectations

that when multiple content classes of images/videos

are in the same dataset, a descriptor will produce

denser regions, containing smaller components with

similar contents.

As it was mentioned, the ratio of the largest and

second largest component is important in relation to

descriptor behaviour,during the building of the graph,

in the search for the point where the single giant

component appears. This ratio (examples shown in

Fig.5 and 6) shows different behaviour w.r.t. simu-

lated datasets, with multiple peak regions during the

process. This solidiﬁes the expectations that different

components growing in parallel will produce separate

denser regions containing inter-similar contents.

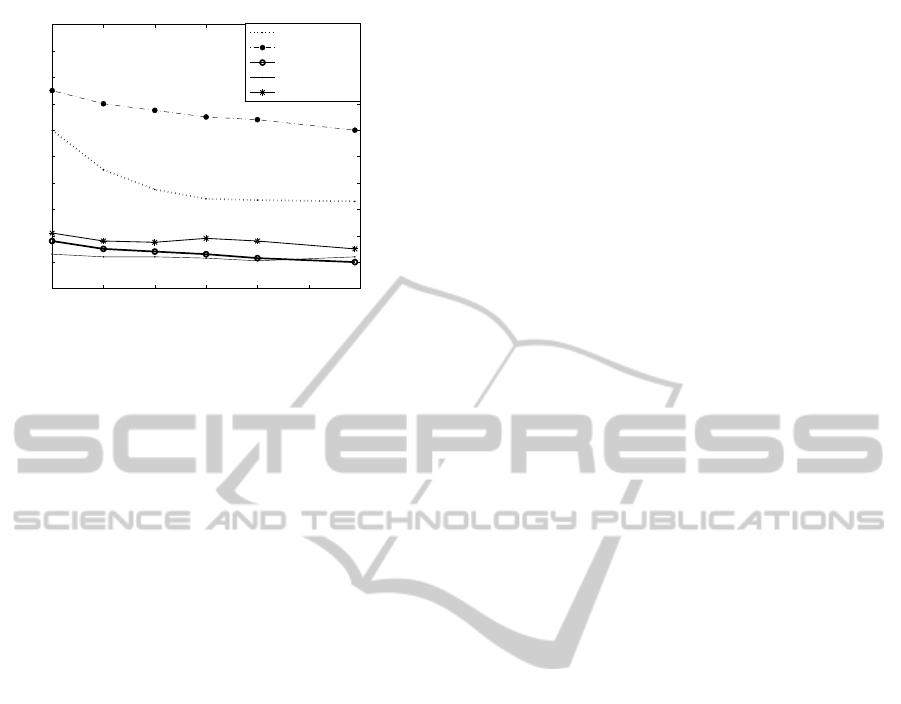
The critical edge weights of some descriptor

graphs are shown on Fig. 7. As shown, the criti-

cal weights depend on the number of vertices of the

graph, but the impact of this parameter depends on the

0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04

0.2

0.4

0.6

0.8

Weight tresholds

Second / largest component size

N=1000

N=2000

N=4000

N=5000

N=6899

Figure 5: Ratio of the second and the largest component

sizes of the Focus histogram graph.

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

0.2

0.4

0.6

0.8

Weight thresholds

Second / largest component size

Average Color

Edge Histogram

Focus

ColorStructure

Curvelets

Figure 6: Ratio of the second and the largest component in

case of different descriptors.

descriptor. Detailed test results on the critical weight

value of the Focus descriptor graph (see Fig.5) shows

how it depends on the size of the graph.

Depending on the task, the estimated values of the

critical edge weights have high importance. For ex-

ample in shortest-paths based clustering task (label

propagation) it is necessary to know whether labels

could spread through the graph - i.e. is the graph con-

nected (or almost connected). In this case the optimal

threshold would be near the phase transition’s critical

value. On the other hand, if we are interested in the

selection of possible cluster cores (dense regions), we

should select a threshold that results in a graph with

GRAPH BASED DESCRIPTOR EVALUATION TOWARDS AUTOMATIC FEATURE SELECTION

379

1000 2000 3000 4000 5000 6000 7000

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

0.2

Number of vertices

Weight thresholds

Average color

Edge histogram

Focus

LBP

Dominant color

Figure 7: Critical weight values in the graph of different

descriptors.

small dense components.

Our work presents the possibility of ﬁnding the

optimal threshold, depending on the selected descrip-

tor. This way we are also able to evaluate the ’quality’

of a descriptor. The lower the critical weight value is,

the smaller the chance of ﬁnding relevant dense clus-

ter cores.

6 CONCLUSIONS AND FUTURE

WORK

This paper presents the ﬁrst steps towards an auto-

matic feature selection framework, investigating de-

scriptor behaviour based on the analysis of random

geometric graphs structures built from real data and

by using element distances based on several descrip-

tors and their distance / difference distributions along

with the generic behaviour of such graph types dur-

ing the appearance of the giant component. Our next

goal is to produce a descriptor evaluation framework

which analyses graph-connectednessweighted by dif-

ference distributions and their relation to the thresh-

olds associated to the estimated appearances of the

giant component, and rank descriptors (and combina-

tions of descriptors) based on these properties. His-

tograms of such distances combined with graph anal-

ysis based on random graph theory can provide a solid

foundation for image and video feature selection.

ACKNOWLEDGEMENTS

This work has been partially supported by Hungarian

Scientiﬁc Research Fund grants 83438 and 80352.

REFERENCES

Candes, E., Demanet, L., Donoho, D., and Ying, L. (2006).

Fast discrete curvelet transforms. Multiscale Model-

ing and Simulation, 5(3):861–899.

Chapelle, O., Vapnik, V., Bousquet, O., and Mukherjee,

S. (2002). Choosing multiple parameters for support

vector machines. Machine Learning, 46(1):131–159.

Comaniciu, D. and Meer, P. (2002). Mean shift: A ro-

bust approach toward feature space analysis. IEEE

Trans. on Pattern Analysis and Machine Intelligence,

24(5):603–619.

Erdos, P. and Renyi, A. (1960). On the evolution of random

graphs. Pbulication of the Mathematical Institute of

the Hungarian Academy of Sciences.

Guldogan, E. and Gabbouj, M. (2008). Feature selection

for content-based image retrieval. Signal, Image and

Video Processing, 2(3):241–250.

Kov´acs, L. and Szir´anyi, T. (2007). Focus area extraction

by blind deconvolution for deﬁning regions of inter-

est. IEEE Tr. on Pattern Analysis and Machine Intel-

ligence, 29(6):1080–1085.

Manjunath, B. S., Ohm, J. R., Vasudevan, V. V., and Ya-

mada, A. (2001). Color and texture descriptors. IEEE

Trans. on Circuits and Systems for Video Technology,

2(6):703–715.

Morris, M. and Kender, J. (2009). Sort-merge feature selec-

tion and fusion methods for classiﬁcation of unstruc-

tured video. In Proc. of IEEE international conference

on Multimedia and Expo, pages 578–581.

Ojala, T. and Pietikainen, M. (2002). Multiresolution gray-

scale and rotation invariant texture classiﬁcation with

local binary patterns. IEEE Trans. on attern Analysis

and Machine Intelligence, 24(7).

Penrose, M. (2003). Random Geometric Graphs. Oxford

University Press.

Setia, L. and Burkhardt, H. (2006). Feature selection for

automatic image annotation. In Proc. of 28th Pat-

tern Recognition Symposium of the German Associ-

ation for Pattern Recognition. Springer.

Shen, Y., Lu, H., and Xue, X. (2007). A semi-automatic

feature selecting method for sports video highlight an-

notation. In Proc. of 9th Intl. Conference on Advances

in visual information systems, pages 38–48.

Sun, Y., Todorovic, S., and Goodison, S. (2010). Local

learning based feature selection for high dimensional

data analysis. IEEE Trans. on Pattern Analysis and

Machine Intelligence, 32(9):1610–1626.

Zhang, W., Men, S., Xu, L., and Xu, B. (2010). Feature

distribution based quick image retrieval. In Proc. of

Web Information Systems and Applications Confer-

ence, pages 23–28.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

380