FEATURE-DRIVEN MAXIMALLY STABLE EXTREMAL REGIONS

P. Martins

, C. Gatta

2,3

and P. Carvalho

Centre for Informatics and Systems (CISUC), University of Coimbra, Coimbra, Portugal

Computer Vision Center, Autonomous University of Barcelona, Barcelona, Spain

University of Barcelona, Barcelona, Spain

Keywords:

Local Feature Detection, Maximally Stable Extremal Regions, Completeness.

Abstract:

The high repeatability of Maximally Stable Extremal Regions (MSERs) on structured images along with their

suitability to be combined with either photometric or shape descriptors to solve image matching problems have

contributed to establish the MSER detector as one of the most prominent afﬁne covariant detectors. However,

the so-called afﬁne covariance that characterizes MSERs relies on the assumption that objects possess smooth

boundaries, a premiss that is not always valid. We introduce an alternative domain for MSER detection

in which boundary-related features are highlighted and simultaneously delineated under smooth transitions.

Detection results on common benchmarks show improvements that are discussed.

1 INTRODUCTION

Vision tasks such as object recognition, view match-

ing, and tracking, just to name a few, are often per-

formed under the use of local descriptors, which are

usually characterized by an invariant response to cer-

tain classes of image transformations. A common

procedure to obtain the invariant description consists

in a preliminary detection of local image regions in a

covariant way, which will provide local patches to be

described in an invariant manner.

In the particular case of afﬁne transformations, the

vision community has been proliﬁc in introducing co-

variant feature detectors as well as invariant descrip-

tors. Detectors such as the Harris-Afﬁne, Hessian-

Afﬁne (Mikolajczyk and Schmid, 2004) or the Max-

imally Stable Extremal Regions (MSERs) algorithm

(Matas et al., 2002) are noteworthy solutions to detect

afﬁne covariant features. For a complete review and

extensive references on this class of regions, we refer

the reader to the work of Tuytelaars and Mikolajczyk

(2008) and references within.

The almost linear complexity of the algorithm,

the repeatable results and the suitability of MSER

to be described by photometric or shape descriptors

(Moreels and Pietro, 2007; Forssen and Lowe, 2007)

have made the MSER detector one of the popular ref-

erences in the literature. Here, we bring into the anal-

ysis the well-known and not so well-known shortcom-

ings of the above mentioned detection. As a result,

we suggest an alternative domain for the detection of

MSERs which will allows us to retrieve a substan-

tially higher number of features and improve the ro-

bustness to blur. Furthermore, the new domain pro-

vides a more reliable summary of relevant image con-

tent via MSERs detection.

2 BACKGROUND AND

MOTIVATION

Before laying out a detailed description of the motiva-

tion behind our study, we will shortly review the basic

concepts and terminology around MSER detection.

2.1 Maximally Stable Extremal Regions

Concisely, a MSER is deﬁned as an afﬁne covariant

image region which is either brighter or darker than

its immediate surroundings and without any particular

shape. For a more formal deﬁnition, let us consider an

image as a mapping I : D → [0, 1], where D ⊂ R

. Let

us also denote the interior and the boundary of a con-

nected componentQ

in D as ∂Q

and int(Q

), respec-

tively. MSERs correspond to a very speciﬁc subset of

connected components in the image domain. They are

said to be extremal because the corresponding pixels

have either higher or lower intensity than all the pix-

els on its boundary: I |

int(Q

)

> c or I |

int(Q

)

< c for a

490

Martins P., Gatta C. and Carvalho P..

FEATURE-DRIVEN MAXIMALLY STABLE EXTREMAL REGIONS.

DOI: 10.5220/0003869204900497

In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 490-497

ISBN: 978-989-8565-03-7

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

given c ∈ [0, 1], which is the value on the boundary.

Thus, Q

represents a maximal connected component

of a level set. Designating the region as stable refers

to the fact that a change of c = c + ∆, with ∆ > 0,

will imply minor changes in the area of the extremal

region. Q

will be coined as maximally stable if the

stability measure

ρ(Q

) =

(1)

attains a local maximum at c (Matas et al., 2002; Kim-

mel et al., 2011).

2.2 MSER Detection: Known

Shortcomings

Probably, the most important property of MSER is its

afﬁne covariance that can be directly inferred from

the covariance of the image level sets with respect to

afﬁne transformations in the image domain. On the

other hand, the afﬁne invariance of the detector’s sta-

bility measure guarantees the afﬁne covariance of the

regions. However, as addressed and shown by Kim-

mel et al. (2011), the aforementioned property pre-

vails only if the boundaries of objects are smooth,

which is not always the case. Additionally, the strat-

egy adopted for the detection of these local features

is based on the assumption that images possess well-

deﬁned structures (MSER features are usually an-

chored on region boundaries (Tuytelaars and Miko-

lajczyk, 2008)). These shortcomings have been re-

ported in the well-known comparative study on afﬁne

covariant features performed by Mikolajczyk et al.

(2005). MSERs – along with Hessian-Afﬁne regions

– have shown to be the most repeatable features in

the overall benchmark. However, the former has evi-

denced an expected less consistent behavior: reason-

ably textured scenes or blurred sequences were prone

to provide less repeatable results. As an example,

Figure 1 illustrates such fragility when a progressive

de-focus blur is present: as it increases, the shape of

MSERs tends to change and, simultaneously, its num-

ber decreases.

Furthermore, the number of features that the

MSER detector retrieves is usually low if we compare

it to the number of local features detected by other

prominent detectors, e.g., Hessian-Afﬁne or Harris-

Afﬁne. We can regard this fact as a shortcoming of

MSER detection, as it might hinder the robustness of

MSERs to occlusions.

A quite less trivial but noteworthy characteristic

of MSER detection derives from the stability mea-

sure (Eq. (1)), which prefers round shapes to irreg-

ular ones. To our knowledge, Kimmel et al. (2011)

Figure 1: MSER detection (bottom row) on the ﬁrst two

images of the “Bikes” sequence (top row). MSERs are rep-

resented by ﬁtted ellipses.

have been the only ones to address the biased pref-

erence for regular shapes. In their paper, the authors

have illustrated this bias by showing that if two re-

gions have the same area and the same intensity along

their boundaries, the measure ρ tends to prefer the one

with a shorter boundary (perimeter). We emphasize

the importance of such property as most scenes con-

tain irregular shapes and we surely cannot claim that

regular shapes are always more distinctive than irreg-

ular ones.

2.3 Related Work: Other MSERs

We have highlighted some of the most important

shortcomings of MSER detection, namely (i) a rela-

tively high sensitivity to blurring, (ii) a small number

of features, and (iii) the preference of the algorithm

towards regular shapes.

A straightforward approach to reduce the sensitiv-

ity of MSER detection to blur is to apply a low-pass

ﬁlter to the input image. Such pre-processing will en-

hance the repeatability of MSERs in the presence of

blurred scenes, whereas the number of features will

be reduced. A more reliable alternative is to make

use of a multi-resolution detection: Forssen and Lowe

(2007) suggest an improved version of the MSER de-

tector by building a scale pyramid with one octave

between scales. MSERs are detected at each resolu-

tion and duplicated features at consecutive scales are

removed by comparing their locations. This strategy

leads to a higher number of detected features and an

improved repeatability under blur and scale changes.

However, it requires MSER features to be detected

at each resolution, which increases the computational

complexity of the method.

With the aim of freeing the MSER detector from

the existent preference towards round shapes, Kim-

mel et al. (2011) propose several reinterpretations of

the stability measure in order to deﬁne more informa-

tive shape descriptors.

FEATURE-DRIVEN MAXIMALLY STABLE EXTREMAL REGIONS

491

3 FEATURE-DRIVEN MSERS

We extend the concept of MSER to an alternative im-

age representation in which certain boundary-related

features are highlighted. MSERs detected on this do-

main will be coined as feature-driven MSERs. The

proposed domain is less sensitive to blurring and al-

lows the MSER detector to respond to a substantially

higher number of features per image. Moreover, ir-

regular shapes will appear more regular in the new

domain. In short, we propose a domain that encapsu-

lates the desired properties to yield a reliable MSER

detection, namely the existence of regular shapes and

well-deﬁned boundaries combined with smooth tran-

sitions. The new domain is also designed to improve

the completeness of MSER features. We can regard

a set of features as a complete one if it preserves as

much as possible the information contained in the im-

age (Dickscheid et al., 2010). Increasing the number

of detected MSERs is not enough to produce a more

complete feature set; the regions should also preserve

the most relevant image content.

In the process of obtaining a domain characterized

by well-deﬁned boundaries, but with smooth transi-

tions, we start by highlighting boundary-related fea-

tures. The process described herein highlights edges

using gradient information, which is a valid source

of information to build the domain with the desired

properties. Other alternatives can be considered for

feature highlighting, e.g., the eigenvalues of the Hes-

sian matrix.

For our purpose, obtaining smooth transitions at

the boundaries is as important as the process of fea-

ture highlighting and the consequent identiﬁcation of

structural regions. The detection of structures at dif-

ferent scales will help us to deﬁne smooth transitions.

The process of averaging information over scales is

the key component to obtain the desired smoothness.

In the domain given as an example, we will highlight

edges and obtain smooth transitions by making use of

the gradient magnitude, computed by means of Gaus-

sian derivatives at several scales. Let L(:,σ) be the

result of convolving I with a Gaussian kernel g with

variance σ

. From the ﬁrst order derivatives of L at

different scales, we obtain a new input for MSER de-

tection:

L(~x) =

∑

i=1

(~x,σ

) + L

(~x,σ

), (2)

where the standard deviation σ

varies in a geomet-

ric sequence σ

= σ

i−1

, with σ

∈ R

, ξ > 1, and

N denotes the number of scales. The ﬁnal image is

the result of averaging gradient magnitude computed

at different scales. By doing this, with a reasonable

Bikes 1 Bikes 3

Input Images

Bikes 1:

L(~x) Bikes 3:

L(~x)

Feature highlighting

Feature-driven MSERS

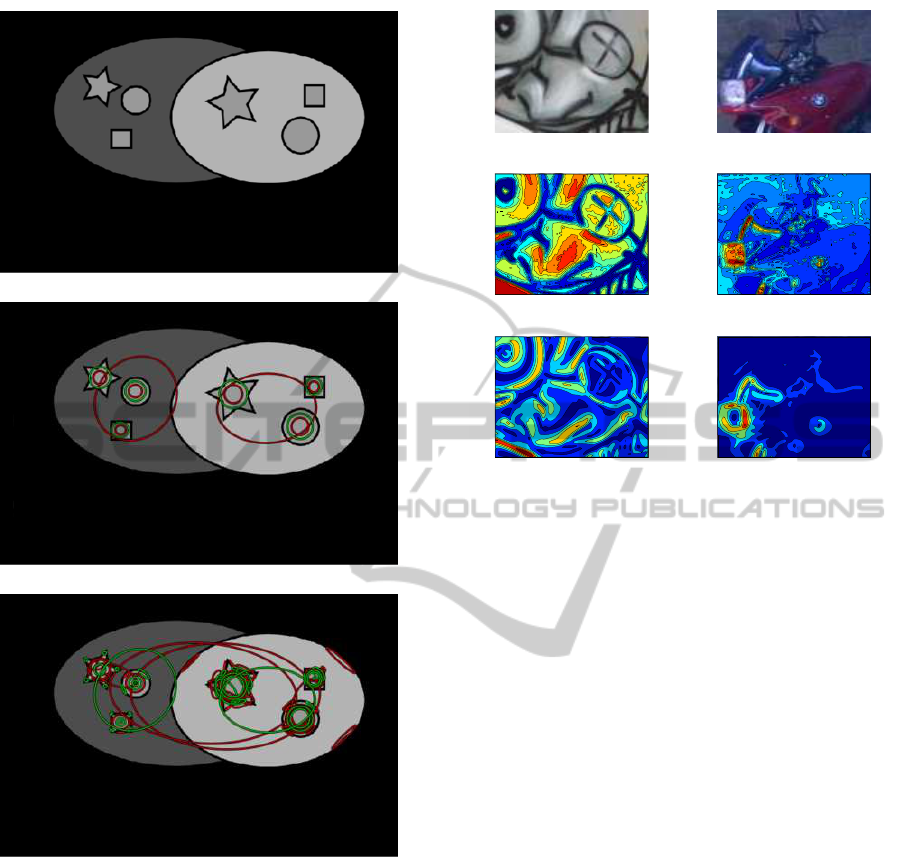
Figure 2: Example of a detection of feature-driven MSERs

using the suggested domain. Detected features are repre-

sented by ﬁtted ellipses.

number of scales, smooth transitions at the edges will

be obtained. Fig. 2 illustrates the suggested detec-

tion on a scene with de-focus blur. It is readily seen

that the new set of MSERs provides a good coverage

of the content and robustness to blur. The detection

depicted in Fig. 3 serves as a more illustrative ex-

ample of the difference between original MSERs and

the proposed ones. For a better comprehension of the

proposed detection and due to the relatively low num-

ber of features detected on the synthetic image, we

distinguish in this example MSER+ features i.e., dark

regions with brighter boundaries, from MSER- fea-

tures, which correspond to bright regions with darker

boundaries. The latter features are obtained by giv-

ing the inverted image as input. As can be seen, the

use of the proposed domain yields a higher number

of MSERs. Furthermore, it allows us to capture in-

formative patterns in the scene such as corners and

junctions, which are usually neglected by a traditional

MSER detection.

The new domain will also attenuate the so-

called irregularity of extremal regions. Figure 4

helps to clearly illustrate the process of attenuation:

the boundaries of extremal regions correspond to

isophotes, i.e., iso-intensity countours. As expected,

these curves tend to appear irregular in shape on the

luminance channel (see Fig. 4-2(a)-(b)), whereas the

new domain providesmore regular shapes (see Fig. 4-

3 (a)-(b)). The examples in this ﬁgure equally demon-

strate that the proposed domain tends to highlight

relevant structures and present them as potential ex-

tremal regions. We can illustrate this fact with the

example of the logo on the motorbike: it appears as

a scattered object on the luminance channel, whereas

the new domain regards it as a relevant structure.

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

492

(a)

(b)

(c)

Figure 3: MSER detection on a synthetic image (green:

MSER+, red: MSER-): (a) input image; (b) original de-

tection; (c) suggested detection.

4 EXPERIMENTAL VALIDATION

We have followed the guidelines given by the bench-

mark suggested by Mikolajczyk et al. (2005) to as-

sess the repeatability of the redeﬁned MSER on pla-

nar scenes. In the literature, repeatability as been re-

garded as the fundamental criterion to assess the per-

formance of local features. Regardless of its impor-

tance, it does not provide a hint on the usefulness

and quality of the features. Therefore, our evalua-

tion has taken into account another important criterion

1 (a) 1 (b)

2 (a) 2 (b)

3 (a) 3 (b)

Figure 4: Isophotes and extremal regions: (1) input images;

(2) regions delineated by isophotes on the luminance chan-

nel; (3) regions delineated by isophotes on the suggested

domain.

that is often neglected: the completeness of features.

Furthermore, we would like to determine the level of

complementarity between MSERs extracted from the

original image and the proposed domain. Special em-

phasis is givento the performance of MSERs on struc-

tured images.

In this section, features that are retrieved using the

gradient-based image

L as the input image for detec-

tion will be referred to as f-MSERs.

Implementation Details. We have made use of the

code provided by Vedaldi and Fulkerson (2008) for

MSER detection, which has been extended to deal

with images intensity values varying in a range dif-

ferent from {0, ... , 255}, as the new domain intensity

values might be greater than 255.

Parameter Settings. In the whole set of experi-

ments, the new domain was built with an initial scale

= 0.64 and ξ = 1.19. N, the number of scales, was

set to 16. The default value for the variation param-

eter ∆ required by the stability measure is 10, as it is

a reasonably low number to give rise to a high num-

ber of features. The protocol that we have followed

evaluates the repeatability rate and the number of cor-

respondences. A less sparse detection often implies a

drop in the repeatability rate, albeit the potential in-

crease in the number of correspondences. For a reli-

FEATURE-DRIVEN MAXIMALLY STABLE EXTREMAL REGIONS

493

Table 1: Oxford dataset sequences.

Sequence Grafﬁti Wall Boat Bark Bikes Trees Leuven UBC

Texture X X X

Transformation Viewpoint Viewpoint Scale Scale Blur Blur Light JPEG

Grafﬁti Wall Boat Bark

Bikes Trees Leuven UBC

Figure 5: Oxford dataset sequences: example images.

able evaluation of these two criteria, detectors should

respond to a comparable number of features. Thus, in

some cases, we report results using additional values

for the variation parameter in the stability measure.

On one hand, the use of several ∆ allows us to have a

more insightful analysis and comparison of the main

results. On the other hand, it is also advantageous

to analyze results for a single (ﬁxed) ∆: we can ex-

pect a higher number of f-MSER features but would

they be more repeatable than MSERs? Moreover, it

is interesting to assess the degree of complementarity

between MSER and f-MSER features when there is a

discrepancy between the cardinalities of sets.

4.1 Repeatability Evaluation

The benchmark suggested by Mikolajczyk et al.

(2005) computes the repeatability between regions

detected on two image pairs using 2D homographies

as a ground truth. Two regions are deemed as corre-

sponding and, therefore, repeated, with an overlap er-

ror of ε

× 100% if 1−



∩R



∪R



< ε

, where µ

and µ

denote the approximating ellipses of the two

detected regions, H is the homography and R

∗

repre-

sents the set of points identiﬁed by its subscript ∗. The

dataset, known as the Oxford dataset, comprises 8 se-

quences of images, each one with 6 images, whose

short description is outlined in Table 1 and depicted

in Fig. 5. One of the main motivations to deﬁne f-

MSERs is to ﬁnd a more repeatable set of features in

structured scenes, even when blur occurs. Figures 7

to 9 depict the repeatability and the correspondence

Figure 6: f-MSERs detected on the ﬁrst and third images of

the “Boat” sequence.

plots for the sequences “Bikes”, “UBC” and “Boat”

(see detection results in Fig. 6), with an overlap er-

ror of 40%. The ﬁrst image in each sequence is used

as the reference. In all the cases, it is clear that f-

MSER features are higher in number without show-

ing a signiﬁcant drop in the repeatability rate. We

would like to stress that a substantially higher num-

ber of correspondences accompanied with a slight de-

crease of the repeatability rate is preferable to a minor

increase of the repeatability with less features, as in

the former the absolute number of repeated features

is considerably higher, which might provide a better

coverage of the content with a similar repeatability

rate. Nonetheless, the sequences of structured images

affected and corrupted by blur or JPEG compression

have shown an improved repeatability rate with the

use of f-MSERs. For the “Boat” sequence, we re-

port a decrease of the repeatability rate of f-MSERs

at higher scales. Nevertheless, the number of repeated

f-MSERs at higher scale changes is comparable to the

number of repeated MSERs.

For space reasons, we will not display all the re-

sults of the experiments in the form of plots. How-

ever, Table 2 gives a hint on the behavior of the de-

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

494

2 3 4 5 6

100

Increasing blur

Repeatability (%)

2 3 4 5 6

200

400

600

800

1000

1200

1400

1600

Increasing blur

Number of correspondences

f−MSER (∆=10)

f−MSER (∆=20)

f−MSER (∆=50)

MSER (∆=10)

MSER (∆=20)

MSER (∆=50)

f−MSER (∆=10)

f−MSER (∆=20)

f−MSER (∆=50)

MSER (∆=10)

MSER (∆=20)

MSER (∆=50)

Figure 7: Repeatability rate and number of correspondences for the “Bikes” sequence (overlap error of 40%).

60 70 80 90 100

100

JPEG compression (%)

Repeatability (%)

60 70 80 90 100

500

1000

1500

2000

2500

3000

JPEG compression (%)

Number of correspondences

f−MSER (∆=10)

f−MSER (∆=20)

f−MSER (∆=50)

MSER (∆=10)

MSER (∆=20)

MSER (∆=50)

f−MSER (∆=10)

f−MSER (∆=20)

f−MSER (∆=50)

MSER (∆=10)

MSER (∆=20)

MSER (∆=50)

Figure 8: Repeatability rate and number of correspondences for the “UBC” sequence (overlap error of 40%).

1 1.5 2 2.5 3

100

Scale changes

Repeatability (%)

1 1.5 2 2.5 3

100

200

300

400

500

600

700

800

Scale changes

Number of correspondences

f−MSER (∆=10)

f−MSER (∆=20)

f−MSER (∆=50)

MSER (∆=10)

MSER (∆=20)

MSER (∆=50)

f−MSER (∆=10)

f−MSER (∆=20)

f−MSER (∆=50)

MSER (∆=10)

MSER (∆=20)

MSER (∆=50)

Figure 9: Repeatability rate and number of correspondences for the “Boat” sequence (overlap error of 40%).

tected regions for the complete dataset. It provides

the repeatability rate and number of correspondences

for the third image of each sequence as well as the cor-

responding average values for each sequence with an

FEATURE-DRIVEN MAXIMALLY STABLE EXTREMAL REGIONS

495

Table 2: Repeatability rate and number of correspondences

for each sequence (overlap error of 40%).

3rd image Sequence

(average)

MSER f-MSER MSER f-MSER

Graﬁtti 56%(310) 48%(538) 48%(244) 39%(402)

Wall 53%(2093) 57%(2484) 46% (1595) 46% (1786)

Boat 48%(658) 56%(861) 41%(388) 39%(556)

Bark 52%(276) 48%(355) 60% (268) 39%(295)

Bikes 47%(505) 58%(1328) 42%(360) 46%(1002)

Trees 38% (1767) 36% (1796) 33%(1295) 30%(1401)

Leuven 57%(668) 58%(901) 57% (488) 54%(768)

UBC 50%(1114) 63%(1647) 42% (825) 51%(1262)

overlap error of 40%. By analyzing the table, one can

conclude that feature-driven MSERs yield a consid-

erably higher number of correspondences. The lower

average repeatability rate of f-MSERs as seen in some

sequences is mainly due to the decrease of the re-

peatability rate in the last images of the sequence. As

theory conﬁrms, in well-structured scenes, the new

MSERs can yield an increased repeatability. With re-

gard to sequences with viewpoint changes, f-MSERs

have shown a satisfactory repeatability. Nonetheless,

this repeatability can be improved if we build the do-

main under an afﬁne scale-space.

4.2 Completeness Evaluation

How much of the image information is preserved

by local features? Feature sets should capture the

most relevant image content in order to provide

a trustworthy summarized description of the im-

age. This requirement is known in the literature

as completeness. A measure of completeness has

been proposed by Dickscheid et al. (2010). Suc-

cinctly, the incompleteness of a detection corresponds

to the following Hellinger distance: d(p

, p

) =

∑

~x∈D

(

(~x) −

(~x))

, where p

corre-

sponds to an entropy density, computed from local

image statistics and p

denotes a feature coding den-

sity, inferred from the set of features. We emphasize

that the completeness measure is not a simple way

of evaluating the image coverage of feature sets; it

penalizes local feature sets that contain less informa-

tive patterns despite of their coverage. For the pur-

pose of the evaluation, we deﬁned a dataset compris-

ing images from the Oxford dataset sequences. Each

sequence was represented by its third image. The pa-

rameter settings for the detection coincide with the

ones used in the previous subsection. Table 3 outlines

the results of the completeness evaluation givenby the

Hellinger distance between the two aforementioned

distributions, using feature coding densities computed

from MSER and f-MSER feature sets as well as a

combination of both sets. The analysis of the latter

feature set results allows us to infer on the comple-

Table 3: Dissimilarity measure d(p

, p

) and number of

regions for the third image of each sequence.

MSER

MSER f-MSER f-MSER+ f-MSER- ∪

f-MSER

Grafﬁti 0.38(1085) 0.27(2216) 0.33(1130) 0.36(1086) 0.26

Wall 0.2(4433) 0.15(4981) 0.24(2711) 0.26(2270) 0.14

Boat 0.35(2319) 0.28(2720) 0.36 (1393) 0.35(1327) 0.27

Bark 0.29(1940) 0.19(2802) 0.27(1553) 0.31(1249) 0.18

Bikes 0.48(1123) 0.32(2388) 0.4(1311) 0.43(1077) 0.32

Trees 0.24(4821) 0.19(5299) 0.29(2529) 0.26(2770) 0.18

Leuven 0.45(1017) 0.36(1597) 0.44(869) 0.46(728) 0.35

UBC 0.29(2431) 0.26(2619) 0.35(1400) 0.35(1219) 0.24

mentarity of MSER and f-MSER features. Addition-

ally, we have analyzed the completeness of f-MSER+

and f-MSER- features. These results are summarized

in the same table.

It is important to note that MSER-like features are

not among the most complete ones (Dickscheid et al.,

2010). It is readily seen that homogeneous regions

are easily entitled to be classiﬁed as extremal regions,

which, in most of the cases, means excluding the most

informative content. Furthermore, the number of fea-

tures detected by the MSER algorithm tends to be

lower than the ones given by other prominent detec-

tors, such as the Hessian-Afﬁne or the Harris-Afﬁne.

One important conclusion to be drawn from Ta-

ble 3 is that f-MSER detection will provide us a

more complete set of features than the one comprised

of standard MSERs. The incompleteness values for

f-MSERs range from 0.15 (“Wall” image) to 0.36

(“Leuven” image), which reﬂects the high level of

completeness of these features. MSER features are

less complete and, in some cases, even less complete

than f-MSER+ or f-MSER- feature sets. The combi-

nation of MSER and f-MSERs features gives us the

most complete feature sets for each sequence. How-

ever, the complementary between both feature sets

is practically non-existent; the incompleteness values

for MSER ∪ f-MSER features are comparable to the

ones for feature-driven MSERs sets. This result helps

us to conclude that the relevant content preserved by

standard MSERs is also preserved by f-MSERs.

5 CONCLUSIONS AND FUTURE

RESEARCH DIRECTIONS

We have addressed the shortcomings of MSER detec-

tion as well as the desired properties of an image in

order to provide a reliable MSER detection. As result,

we have introduced an alternative domain for MSER

detection. This domain is mainly characterized by the

highlighting of certain boundary-related features and

the simultaneous presence of smooth transitions at the

boundaries. The detection of MSERs on this domain

responds to a higher number of regions than the one

VISAPP 2012 - International Conference on Computer Vision Theory and Applications

496

that uses the luminance channel as input. The feature-

driven MSERs tend to be more robust to blur than tra-

ditional ones. Furthermore, the new set of features

is more complete as it preserves more of the relevant

image content. The high level of completeness shown

by the feature-driven MSERs suggests that they can

be used to solve object recognition problems.

The new domain can be built with any func-

tion that responds to boundary-related features, which

gives several options to work with. In this paper, we

have used the gradient magnitude to build it and, as

future research directions, we intend to exploit other

measures to derive the domain. Future work also

includes assessing the performance of feature-driven

MSERs on object recognition problems.

REFERENCES

Dickscheid, T., Schindler, F., and F¨orstner, W. (2010). Cod-

ing images with local features. International Journal of

Computer Vision (in press).

Forssen, P.-E. and Lowe, D. (2007). Shape Descriptors for

Maximally Stable Extremal Regions. In Proc. of IEEE

11th Int. Conf. on Computer Vision, pages 1–8.

Kimmel, R., Zhang, C., Bronstein, A., and Bronstein, M.

(2011). Are MSER features really interesting? IEEE

Trans. on Pattern Analysis and Machine Intelligence,

33(11):2316–2320.

Matas, J., Chum, O., Urban, M., and Pajdla, T. (2002).

Robust wide baseline stereo from maximally stable ex-

tremal regions. In Proc. of the British Machine Vision

Conference 2002 (BMVC 2002), pages 384–393.

Mikolajczyk, K. and Schmid, C. (2004). Scale & afﬁne

invariant interest point detectors. International Journal

of Computer Vision, 60(1):63–86.

Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,

Matas, J., Schaffalitzky, F., Kadir, T., and Gool, L. V.

(2005). A Comparison of Afﬁne Region Detectors. In-

ternational Journal of Computer Vision, 65(1/2):43–72.

Moreels, P. and Pietro, P. (2007). Evaluation of Features

Detectors and Descriptors based on 3D Objects. Int. J.

Comput. Vision, 73(3):263–284.

Tuytelaars, T. and Mikolajczyk, K. (2008). Local invari-

ant feature detectors: a survey. Found. Trends Comput.

Graph. Vis., 3(3):177–280.

Vedaldi, A. and Fulkerson, B. (2008). VLFeat: An

open and portable library of computer vision algorithms.

http://www.vlfeat.org/.

FEATURE-DRIVEN MAXIMALLY STABLE EXTREMAL REGIONS

497