A COMBINED TECHNIQUE FOR DETECTING OBJECTS IN
MULTIMODAL IMAGES OF PAINTINGS
Dmitry Murashov
Dorodnicyn Computing Centre of RAS, Vavilov st. 40, 119333, Moscow, Russian Federation
Keywords: Multimodal Images, Information-theoretical Image Difference Measure, Fine-art Paintings, Object
Detection.
Abstract: A combined technique for detecting objects in multimodal images based on specific object detectors and
image difference measure is presented. The information-theoretical measures of image difference are
proposed. The conditions of applicability of these measures for detecting artefacts in multimodal images are
formulated. The technique based on the proposed measures is successfully used for detecting repainting and
retouching areas in the images of fine-art paintings. It requires segmentation of only one of the analyzed
images.
1 INTRODUCTION
In this paper, a problem concerned to analysis of
images taken in different spectral bands is
considered. Multispectral images are widely used in
restoration and attribution of paintings. Images
obtained in different modalities provide information
invisible for the human eye (Kirsh, 2000). For
example, ultraviolet (UV) fluorescence shows newly
applied materials (repainting or retouching area, see
Figure 1; the painting is kept at the Historical State
Museum, Moscow). One of the problems that should
be solved to support formulating restoration tasks is
the discovery and localization of repainting or
retouching areas. It is necessary to detect objects or
artefacts in UV image and find their corresponding
position in visible image.
The images under research are the JPEG images
of size 1640 by 1950 pixels and of 8 or 24 bpp
depth. Properties of the images under research affect
the solutions of the problem. First, uneven
illumination of painting. Second, regions of interest
have various intensity profiles and contrast. Third,
the objects may differ in size from tens to several
hundreds or even thousands of pixels. Forth, a
variety of shapes and intensity levels of the objects.
Hence the regions of interest may be partitioned into
classes according to their appearance in images, and
different detectors should be applied. We will
consider two images U and V of size mn of the
same scene acquired in different spectral ranges and
quantized by K and L gray levels respectively. Let us
assume that K objects (or artefacts)
U
k
O , k = 1, …,K,
are visible in image U, and L objects
V
l
O
, l = 1,…,L,
are visible in V. Objects
U
k
O and
V
l
O are considered
to be the connected sets of pixels having k and l gray
values respectively. It is necessary to localize
objects
U
k
O
visible in image U and absent in V.
(a) (b)
Figure 1: Images of the painting taken in optical (a) and
UV (b) spectral bands.
For solving the problem, the following strategy is
proposed: (a) a measure of image difference will be
introduced; (b) taking into account the specificity of
the appearance of repainting areas in ultraviolet
image, the dark objects will be localized using
specific detectors; (c) applying the image difference
measure, the repainting areas will be selected from
727
Murashov D..
A COMBINED TECHNIQUE FOR DETECTING OBJECTS IN MULTIMODAL IMAGES OF PAINTINGS.
DOI: 10.5220/0003870107270732
In Proceedings of the International Conference on Computer Vision Theory and Applications (VISAPP-2012), pages 727-732
ISBN: 978-989-8565-03-7
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

the objects detected at step (b). Some of the
previously developed approaches to detecting
differences in images are briefly observed in the
next section.
2 RELATED WORKS
In paper (Minakhin, 2009), for detecting damages of
negatives obtained in the technique of three-color
photography, a procedure based on the logical
operations with binary images is used. The
procedure is computationally expensive for large
images and does not provide the reliable detection.
In (Heitz, 1990), a method for automated detection
of hidden information (so-called “events”) using
photograph and X-ray image of painting is
described. Detection of “events” is based on the
analysis of two-level hierarchical description of the
image pair. The method seems to be rather
computationally expensive, because it requires
segmentation and feature extraction in each image of
the pair. In (Daly, 1993, Petrovic, 2004), the authors
evaluate visual differences in images and
multispectral image sequences utilizing the human
visual system model. The problem formulation of
evaluating visual differences in images does not
fully meet the problem considered in this paper,
which is dealing with detection of objects visible
only in one image and invisible in another. In
(Kammerer, 2004), the authors developed a software
tool for visual examination and comparison of IR
photographs and color image to support art
historians in understanding differences and
similarities of the preliminary scetches and the final
painting. The study of the existing approaches has
shown that the efficient technique for solving the
problem considered in this paper has not been
developed to date. In several works, information-
theoretical techniques are used for evaluation of
similarity and differences of images.
In the next section, information-theoretical
measures of image difference will be concidered.
3 INFORMATION MEASURES
Information techniques work directly with image
data and no preprocessing or segmentation is
required. In works (Viola, 1995; Escolano, 2009,
and many others), the mutual information measure
of image similarity for multimodality image
registration is presented. In paper (Zhang, 2004), a
new information pseudo metric is introduced. The
metric used is a sum of conditional entropies
H(X|Y)+H(Y|X), where X and Y are random
variables denoting grayscale values at pixels in two
images. In (Rockinger, 1998), to evaluate the
temporal stability and consistency of the fused
image sequence, a quality measure based on the
mutual information is proposed.
In this paper, unlike the image registration and
image fusion problems, it is necessary to use a
measure providing detection of objects visible only
in one image and invisible in the second image of
the analyzed pair. Therefore the required measure
should not be simmetric.
For using information-theoretical approach, the
stochastic model of relation between the images is
needed. Let the grayscale values in the images of
different modalities at a point (x,y) are described by
discrete random variables U(x,y) and V(x,y)
quantized into a finite number of levels K and L, and
taking the discrete values u and
v. As the images U
and V fix the same scene of the real world, there
exist a relation between variables U(x,y) and V(x,y).
A model, analogous to one given in (Escolano,
2009) will be used:
( ( , )) ( ( , )) ( , ),UTrxy FV xy xy



(1)
where Tr is the coordinate transformation (for
registered images we have U(Tr(x,y))=U(x,y)); F is
the function of gray level transform, giving relation
between the images of two modalities;
(, )
x
y

is a
random variable modeling appearance of artefacts.
Expression (1) is considered as a model of a discrete
stochastic information system with input V and
output U. Conditional entropy is defined as follows:
11
(,)
(|) (,)log ,
()
KL
kl
kl
kl
l
pu v
HU V pu v
pv






(2)
11
(,)
(|) (,)log ,
()
KL
kl
kl
kl
l
pu v
HV U pu v
pu






(3)
where
()
k
pu , ()
l
pv are the probability mass
functions of variables U and V, and
(,)
kl
pu v is the
joint probability mass function (p.m.f.) of these
variables.
We propose to use conditional entropies
(|)HU V
and
(|)HV U
for estimating difference of
image U from V. The following statement gives the
conditions for using
(|)HV U
as a measure of
image difference.
Statement 1. The difference of images U and V can
be measured by the conditional entropy
(|)HU V
if
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
728

the following conditions are satisfied:
() ( ,)
lkl
pv pu v ,
1,..., ; 1,...,kKlL
,
(4)
or
() ( ,)
lkl
pv pu v and () (,)
kkl
pu pu v ,
1,..., ; 1,...,kKlL,
(5)
where
()
k
pu , ()
l
pv , (,)
kl
pu v are the probability
mass functions.
The proof of the statement follows directly from
expression (2). The following examples illustrate the
statement. Let K objects
U
k
O , k = 1, …,K are visible
in image U, and L objects
V
l
O , l = 1,…,L in V.
Images U and V are registered. Let the condition (4)
be valid. In this case,
(|)0HU V 
(see expression
(2)). This gives
UVUV
kkkk
OOOO for
1 kM
,
M
K , and
\
UV
kl
OO
for
M
kK , KlL (see Figure 2). The joint
histogram of U and V is shown in Figure 3.
Figure 2: Images U and V provide
(|) 0HU V

.
Figure 3: Joint histogram of images U and V shown in
Figure 2.
Let the condition (5) be valid. Then
UVUV
llll
OOOO
,
1 lM
,
M
L

and
\
VU
lk
OO for
M
lL (see Figure 4). The
joint histogram of images U and V is shown in
Figure 5. In this case,
(|)0HU V 
and its value
depends on the values of corresponding probability
mass function defined by the geometry of the
objects. If
() (,)
kkl
pu pu v then
(|)HU V
will
include information about the objects visible in V
and invisible in U, that does not meet the formulated
requirements to
(|)HU V
.
Figure 4: Images U and V provide
(|) 0HU V 
.
Figure 5: Joint histogram of images U and V shown in
Figure 4.
For the analysis of image pairs it is necessary to
localize and visualize the differences. The value
(|)HU V
computed with the specified number of
quantization levels in the neighborhood of each pixel
of images under research, can be used as an
indicator of artefacts in image U. A size of the
neighborhood and a number of grayscale levels are
chosen in order to: (a) satisfy conditions (4)-(5); (b)
correctly estimate probability mass functions; (c)
provide reasonable precision of difference
localization. Probability mass functions are
estimated using the joint histogram of the image pair
(Rajwade, 2006).
An example of application of measure
(|)HU V
is shown in Figure 6. A color image with objects
embedded in blue channel (a), red channel (b), and
blue channel (c) are presented. Here, blue channel is
denoted as U and red channel is denoted as V. In
Figure 6(d) one can see that all of the embedded
artefacts in the fragment “sky” are detected using
entropy
(|)HU V
and failed to be detected in the
textured regions “forest” and “field” having high
dispersion of grayscale values. It is impossible to
choose the size of pixel neighborhood and number
of quantization levels to satisfy the conditions (4)-
(5). In this case, the efficient way to detect artefacts
is to use entropy
(|)HV U
defined by (3).
The following statement provides conditions for
using
(|)HV U
as a measure of image difference.
Statement 2. The difference of images U and V can
be measured by the conditional entropy
(|)HV U
if
the following conditions are satisfied:
() (,)
kkl
pu pu v ,
1,..., ; 1,...,kKlL


,
or
(6)
u
1
v
1
v
2
u
2
u
3
u
1
v
1
v
2
v
3
u
2
v
2
v
1
u
2
u
3
u
1
v
2
v
1
v
3
u
2
u
1
A COMBINED TECHNIQUE FOR DETECTING OBJECTS IN MULTIMODAL IMAGES OF PAINTINGS
729

() ( ,)
lkl
pv pu v , and () (,)
kkl
pu pu v ,
1,..., ; 1,...,kKlL, and
(7)
00 0
1
:() (,)
L
l
l
upu puv



, 1,...,lL .
(8)
The proof follows directly after substituting
expressions (6-8) to (3).
(a)
(b)
(c)
(d)
Figure 6: A color image with objects embedded in blue
channel (a), red channel (b), blue channel (c), visualized
local values of
(|)
H
UV
(d).
Condition (6) provides
(|) 0HV U 
if U and V
are identical. Conditions (7-8) give
(|) 0HV U 
if
U contains the object invisible in V. Condition (8)
gives
0
UV
l
OO for 1,...,lL (see
Figure 7 (a, b)). The local values of entropies
(|)HU V
and
(|)HV U
are shown in Figure 7 (c, d).
(a) (b) (c)
(d)
Figure 7: Images U and V (a, b); visualized local values of
(|)
H
UV
(c) and
(|)
H
VU
(d).
An example of applying the measure
(|)HV U
to a
fragment of color photograph with high dispersion
values is shown in Figure 8.
(
a)
(b)
Figure 8: (a) Region “field” of the image given in Figure
6(a); (b) visualized local values of
(|)
H
VU
.
The proposed measures of image difference were
tested using color image of size 988 by 1631 pixels
(see Figure 6 (a)) with uniform and textured regions
(sky, forest, field). 140 blurred dark disks of
diameter d from 4 to 8 pixels were embedded in one
of the color channels (see Figure 6(c)). All of the
disks of diameter d = 8 pixels were detected using
measures
(|)HU V
and
(|)HV U
. The results of
the experiment for embedded objects of d = 4 pixels
are shown in Table 1.
The measures were also tested on twenty images
taken from Berkeley Segmentation Dataset
BSDS500. Fifty four blurred dark disks of diameter
of 4 and 8 pixels were embedded into one of the
color channels. All of the objects of d = 8 pixels
were detected. In the average, more than 95% of the
objects of d = 4 were successfully localized.
The results of calculating image difference
measures in noisy image data (see Figure 1) have
shown that it is impossible to obtain a mask of the
objects with required accuracy without utilization of
special detectors. In the next section, a combined
technique based on specific object detectors and
information-theoretical image difference measure is
presented.
4 APPLICATION TO THE
IMAGES OF PAINTINGS
The proposed information-theoretical measure of
image difference
(|)HU V is applied to the task of
detecting regions of intrusion into the author’s paint
layer of fine-art paintings using images in ultraviolet
and visible spectral bands. The input images are
shown in Figure 1 (a, b). We assume that the images
are perfectly registered and uneven illumination is
compensated. The repainting areas appear as dark
spots in UV image (see Figure 1(b)) and practically
invisible in the photograph (see Figure 1 (a)). Taking
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
730

into account the properties of the objects of interest
(see Introduction), detectors of two types are applied
to the grayscale version of ultraviolet image.
Table 1: The results of the test for d = 4.
Image region Number of objects Detected objects Percentage
Sky 68 66 97
Forest 28 27 96
Field 44 40 91
Total 140 133 95
The first detector is aimed on localizing large
dark regions (so-called “basins”) and is based on the
operation of morphological grayscale reconstruction
(Soille, 2004). Let U be a grayscale version of
ultraviolet image of the painting. A mask of the dark
regions is obtained as:
1
(),
U
bas dom
MTUU
(9)
where T() is the threshold operation,
dom
U and
bas
U
are the images of grayscale “domes” and “basins”
found in U:
(),
dom U
UURUg

 
(10)
where
()
U
RU g

 is the result of morphological
reconstruction by geodesic dilation of mask U from
marker U-g; g is the relative height of the domes.
bas
U is found as follows:
(),
bas U
URUhU


(11)
where ( )
U
RU h

 is the result of morphological
reconstruction by geodesic erosion of mask U from
marker U+h; h is the relative depth of the basins.
Operation of pixel-by-pixel subtraction in (9) is used
for enhancing contrast of the image
bas
U .in order to
increase the accuracy of thresholding.
The second detector is intended for localizing
rather small image objects. The algorithm is based
on the locally adaptive thresholding technique
proposed in (Niblack, 1986). The detecting function
is defined in the following way:
1, ( , ) ;
(, )
0, ( , ) ,
M
M
uxy u
xy
uxy u







(12)
where
(, )
M
uuxyq

; (, )uxy is the mean
value of grayscale levels in some neighbourhood of
a point (x,y);

is the standard deviation; q is a
constant. The mask image is defined as follows:
2
(, ) (, )
U
M
xy xy   .
(13)
The images of the binary masks obtained using
detectors described by the expressions (9-11) and
(12-13) are shown in Figure 9.
(a)
(b)
Figure 9: Images of binary masks (a)
1
U
M
and (b)
2
U
M
of
the objects found in UV image.
Not all of the detected objects correspond to the
regions of interest. The next step of the approach is
selecting the repainting areas from the objects
detected at the previous step. For this purpose we
will extract markers using image difference measure
proposed above. Visualized local values of entropies
(|)HU V and
(|)HV U
calculated for the grayscale
versions of input images shown in Figure 1, are
presented in Figure 10(a, b). Probability mass
functions are estimated for 64 grayscale levels in
11x11 windows, and the entropies are calculated in
3x3 pixel neighbourhood. For obtaining markers of
the required objects the following operation is
necessary:
|
( , ) ( ( | ) ( ) ( | )),
UV
MxyTHUVHUHVU (14)
where T() is the threshold operation,
()HU is the
entropy of the ultraviolet image,
() is the operation
of pixel-by-pixel image multiplication. Operations
of image multiplication and subtraction improve
contrast of the thresholded image and increase the
accuracy of thresholding. The mask of the required
objects visible only in UV image can be as:
|
(,) ( )
UV
M
U
MUV R M


,
(15)
where
12
UUU
M
MM; “  ” is the logical “OR”
operation. The obtained mask (15) of the objects
visible only in UV image is shown in Figure 11(a).
The mask combined with image in the optical
spectral range is presented in Figure 11(b). The
proposed combined technique was successfully
A COMBINED TECHNIQUE FOR DETECTING OBJECTS IN MULTIMODAL IMAGES OF PAINTINGS
731

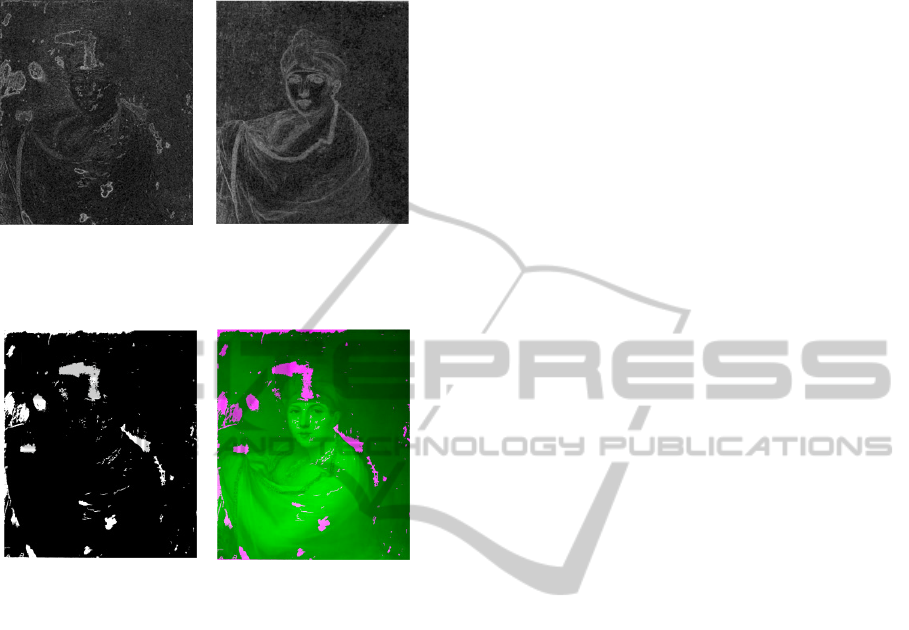
applied to eight pairs of UV and visible images of
fine-art paintings.
(
a)
(b)
Figure 10: Visualized local values of conditional entropies
(|)
H
UV
(a) and
(|)
H
VU
(b).
(a)
(b)
Figure 11: The resultant mask of the repainting areas (a)
and the mask combined with the photograph of the
painting (b).
5 CONCLUSIONS
The combined technique for detecting objects in
multimodal images based on specific object
detectors and image difference measure is presented.
Two information-theoretical measures of image
difference are proposed. The conditions of
applicability of these measures for detecting
artefacts in multimodal images are formulated. The
computing experiment has shown the efficiency of
the proposed measures. The combined technique is
successfully applied for detecting repainting and
retouching areas of fine-art paintings. The objects
having grayscale relief similar to the relief of the
repainting area are localized in UV image thought
the instrumentality of specific detectors.
Subsequently, the “true” objects are selected using
considered information-theoretical difference
measure. The proposed technique requires
segmentation of only one of the analyzed images,
unlike the technique described in (Heitz, 1990). The
future research will be aimed at the development
automated procedures for choosing window size and
number of quantization levels for estimating
conditional entropies.
ACKNOWLEDGEMENTS
This work was supported by the Russian Foundation
for Basic Research, grant No 09-07-00368.
REFERENCES
Daly S., 1993. The visible differences predictor: an
algorithm for the assessment of image fidelity. Digital
images and human vision, MIT Press, Cambridge.
Escolano, F., Suau, P., Bonev, B., 2009. Information
Theory in Computer Vision and Pattern Recognition.
London: Springer Verlag.
Heitz, F., Maitre, H. de Couessin, C., 1990. Event
Detection in Multisource Imaging: Application to Fine
Arts Painting Analysis. IEEE trans. on acoustics,
speech, and signal processin, 38(1), 695-704.
Kammerer, P., Hanbury, A., Zolda, E., 2004. A
Visualization Tool for Comparing Paintings and Their
Underdrawings. In EVA’2004, Conference on
Electronic Imaging & the Visual Arts, 148–153.
Kirsh, A., and Levenson, R. S., 2000. Seeing through
paintings: Physical examination in art historical
studies. Yale U. Press, New Haven, CT.
Minakhin, V., Murashov, D., Davidov, Yu., Dimentman,
D., 2009. Compensation for Local Defects in an Image
Created Using a Triple-Color Photo Technique.
Pattern Recognition and Image Analysis: Advances in
Mathematical Theory and Applications. MAIK
"Nauka/Interperiodica". 19, 1. 137 – 158.
Niblack, W., 1986. An Introduction to Digital Image
Processing. Prentice Hall, Englewood Cliffs, NJ.
Petrovic, V., Xydeas, C., 2004. Evaluation of Image
Fusion Performance with Visible Differences.
ECCV'2004, LNCS, 3023, 380-391.
Rajwade, A., Banerjee, A., Rangarajan, A., 2006.
Continuous Image Representations Avoid the
Histogram Binning Problem in Mutual Information
Based Image Registration, Proc. of IEEE International
Symposium on Biomedical Imaging (ISBI). 840-843.
Rockinger, O., Fechner, T., 1998. Pixel-Level Image
Fusion: The Case of Image Sequences. SPIE Proc.
Signal Processing, Sensor Fusion, and Target
Recognition VII, Ivan Kadar, Editor, 3374, 378-388.
Soille,;P., 2004. Morphological Image Analysis:
Principles and Applications, Springer-Verlag. Berlin.
Viola, P., 1995. Alignment by Maximization of Mutual
Information. PhD Thesis, MIT.
Zhang, J., Rangarajan, A. 2004. Affine image registration
using a new information metric. In: IEEE Computer
Vision and Pattern Recognition (CVPR), 1, 848-855.
VISAPP 2012 - International Conference on Computer Vision Theory and Applications
732