NUMERICAL ANALYSIS OF IMAGE BASED HIGH

THROUGHPUT ZEBRAFISH INFECTION SCREENS

Matching Meaning with Data

Alexander E. Nezhinsky

, Esther Stoop

, Astrid van der Sar

and Fons J. Verbeek

Imaging and Bioinformatics, Leiden University, Leiden Institute of Advanced Computer Science, Niels Bohrweg 1,

2333CA, Leiden, The Netherlands

Department of Medical Microbiology and Infection Control, VU University Medical Center, van der Boechorststraat 7,

1081BT, Amsterdam, The Netherlands

Keywords: Image Analysis, Pattern recognition, Clustering and Classification.

Abstract: Tuberculosis is an ancient disease; however, the molecular mechanism of tuberculosis pathology is not

completely elucidated yet. In our research we aim to contribute to the understanding of the genes/proteins

that are involved in the infection. As a model for the infection study we use the bacterium Mycobacterium

marinum, which is closely related to Mycobacterium tuberculosis, the causative agent of tuberculosis in

humans. M. marinum causes tuberculosis like disease and is applied to the zebrafish larva as a model (host)

organism. We are using a novel pattern recognition framework which allows for in depth analysis of the

spread of infection within the zebrafish organism. The amount of infection has been analyzed. However, in

depth analysis of the spatial distribution was not yet accomplished. Therefore, as a proof of concept we

investigate the presence of specific spatial and quantitive infection patterns.

1 INTRODUCTION

Tuberculosis is a serious disease and a significant

part of the world population is infected.

Unfortunately, effective treatment is still difficult

due to bacteria resistance. In order to elucidate

which genes are responsible for infection, the

behavior of the tuberculosis bacteria -

Mycobacterium tuberculosis needs to be analyzed.

In our study this behavior is modeled by a close

relative – the Mycobacterium marinum (Mm). The

Mm is hosted in cold blooded animals. For our study

the zebrafish is used as a host. Zebrafish makes a

good model for analysis as its immune system is in

many ways comparable to human. The zebrafish

larvae can be obtained in large numbers and studied

by fluorescent imaging. In this matter a visual

inspection of bacteria can be obtained.

Infection of the zebrafish with Mm is

characterized by the presence of granulomas.

Granulomas are clusters of immune cells and

bacteria indicating infection. They can be visualized

with fluorescent agents.

In order to determine which genes of Mm are

involved in formation of granulomas we created

1000 random mutants of the Mm bacteria and

screened for those mutants that were not able to

efficiently infect zebrafish larvae (Stoop et al.,

2011). We have identified 30 mutant bacteria unable

to infect larvae.

In order to gain more insight on the progression

of Mm infection it is required to analyze infection

spread in the host, c.q. the zebrafish, over a certain

period of time. This requires the following questions

to be answered: (1) Is there a pattern in the

appearance of granuloma clusters in certain tissues,

(2) does appearance differ in bacterial mutants.

The analysis is accomplished though imaging.

For each zebrafish a bright field and fluorescence

microscopy image is acquired. Until recently, these

images were analyzed manually. The analysis

included localization of the zebrafish shape and

qualitative estimation of the granuloma cluster size

and spread. Consequently, no objective numerical

data could be retrieved.

We have designed and implemented an

automated framework for shape retrieval and cluster

analysis (Nezhinsky and Verbeek, 2011). This

framework has been applied in large scale

applications (Stoop et al., 2011).

257

E. Nezhinsky A., Stoop E., van der Sar A. and J. Verbeek F..

NUMERICAL ANALYSIS OF IMAGE BASED HIGH THROUGHPUT ZEBRAFISH INFECTION SCREENS - Matching Meaning with Data.

DOI: 10.5220/0003872902570262

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 257-262

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

The framework is based on an algorithm for

shape retrieval (Nezhinsky and Verbeek, 2010) to

automatically find the zebrafish shape(s) in the

image. The algorithm uses deformable template

matching (Jain et al., 1998) and labels the regions

for further analysis. This approach made it possible

to analyze the infection amount per fish in an

automated fashion.

As a proof of principle, a study for the detailed

analysis was performed to find a strategy for

analysis. As a test case we have chosen mutant 714,

as it is one of the 30 mutants which does not make

the fish ill. We are focusing on the question: can we

analyze the spread and size of the granuloma

clusters after infecting the zebrafish. In addition, we

compare similarity in larvae infected with the wild

type Mm and mutant 714.

2 DATASET

The dataset we have used for the analysis consisted

of 189 infected zebrafish larvae. The larvae were

divided into 3 groups: not infected larvae [NI](5),

infected with Mycobacterium marinum [MM](67)

and those infected with the 714 mutant [714M]

(117).

For the infection approximately the same amount

of bacteria was used; the volume was plated on

7H10 plates. At injection the zebrafish were 6 days

old; the imaging was done 5 days past infection

injection.

2.1 Microscopy

Images of wells containing zebrafish were acquired

with a Leica DC500 microscope. During the

experiment up to 3 zebrafish larvae were present in a

single well, as a result a single image can contain up

to 3 individuals.

For each well, both bright field and fluorescent

images were acquired. The bright field image

contains the zebrafish shape, while the fluorescent

image contains the signal at granuloma locations. An

example of such images for a single well is

presented in Figure 1 and 2. As can be seen the

fluorescent images have very low (and different)

intensity values, which makes consistent manual

analysis very difficult and imprecise.

Images were taken in batches of 30 wells. Each

batch contained sibling zebrafish larvae of the three

groups in the same imaging settings.

Figure 1: A bright field image containing up to 3 shapes of

the zebrafish larva.

Figure 2: A fluorescent image containing the signal of

granuloma spread. For visualization purposes the contrast

is enhanced.

2.2 Software

The images are the input for the analysis framework

(Nezhinsky and Verbeek, 2011), which consisted of

two steps. First the zebrafish are localized and the

result is used as a mask for the fluorescent image.

Within the mask a threshold value is determined.

Finally the data is analyzed and written to a comma

separated file.

2.2.1 Bright Field imaging: Shape

Localization and Annotation

The algorithm is applied to the bright field images so

as to obtain a were region of interest (ROI) and

annotation of the relevant areas. A deformable

template was used for the retrieval of the zebrafish

shapes. In order to be able to detect different regions

of the fish, the template was divided in 11 parts

counting from head to tail (numbered from 0 to 10).

This allows annotating the shape as well as doing

spatial analysis. In Figure 3 the graphical

representation of a prototype template (Felzenwalb,

2003) used for our experiments is shown. Parts 0

and 1 can be seen as the head region, 2 till 4 as the

trunk region and other slices as the tail region. This

division of the larva in parts is inspired from the

literature (Volkman et al., 2004). The injection site

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

258

of infection is located at approximately part 5

(Cosma et al., 2006).

Figure 3: Graphical representation of the prototype

template used for our experiments. The template is created

from averaging a test set of 20 training shapes(Cootes et

al.,1994).

2.2.2 Fluorescent Imaging: Analysis

For the actual measurement of clusters fluorescent

images were used and related to the mask size,

obtained from the bright field images.

The NI group is expected to have no infection at

all and thus the level of their maximal fluorescent

signal is considered as noise level n. No infection/

granuloma formation is present at NI, therefore this

group was only used to obtain a noise level

reference. In the other groups all signal below n is

considered noise, while all signal above represents

granuloma presence. This signal is analyzed per fish

and written to an csv file as shown in Table 1

2.2.3 Output and Dataset Creation

Output is created in the form of an overlay image

containing the found zebrafish and infection as

shown in Figure 4 and csv file.

Figure 4: Graphical output of the framework overlaid on

the original image for the top fish in the image. The

magenta line denotes the shape mask contour and the blue

regions indicate the presence of granuloma formation.

This image is created in an automated fashion.

Table 1: Fields contained in the output csv per larva.

Field name Explanation

TotalArea Total shape area

ClusterCount (CC)

Total amount of

clusters in the larva.

ClusterTotalSize (CS)

Total sum of the area

covered by all clusters.

ClusterCountAt[#]

(CC[#])

Like ClusterCount but

measured for a single

template part.

ClusterTotalSize[#]

(Short: CS[#])

Like ClusterTotalSize

but measured for a

single template part.

Clusters of bacteria are labeled and for each of the

clusters the surface area is determined (CS[#]). The

total area (CS) of the spread is the sum over all

clusters. From the template we define 11 parts and a

cluster is always assigned to the part center with

closest geometrical distance (Nezhinsky and

Verbeek, 2010). In Figure 5 we show the part

centers as they are annotated on the fish.

Figure 5: Output for a single zebrafish larva. The yellow

dots denote the annotated part centers.

3 ANALYSIS AND RESULTS

In this section an analysis of the results is presented.

First the distribution of the clusters is discussed and

second a relation to the amount of infection is

established from the data.

3.1 Distribution of Cluster Amount

In our study we set out to analyze the relationship

between mutant and wild type in the amount of

clusters and spatial distribution. To that end we

compare the average number of clusters (

CC[]

variable) between MM and 714 (cf. Figure 6).

NUMERICAL ANALYSIS OF IMAGE BASED HIGH THROUGHPUT ZEBRAFISH INFECTION SCREENS -

Matching Meaning with Data

259

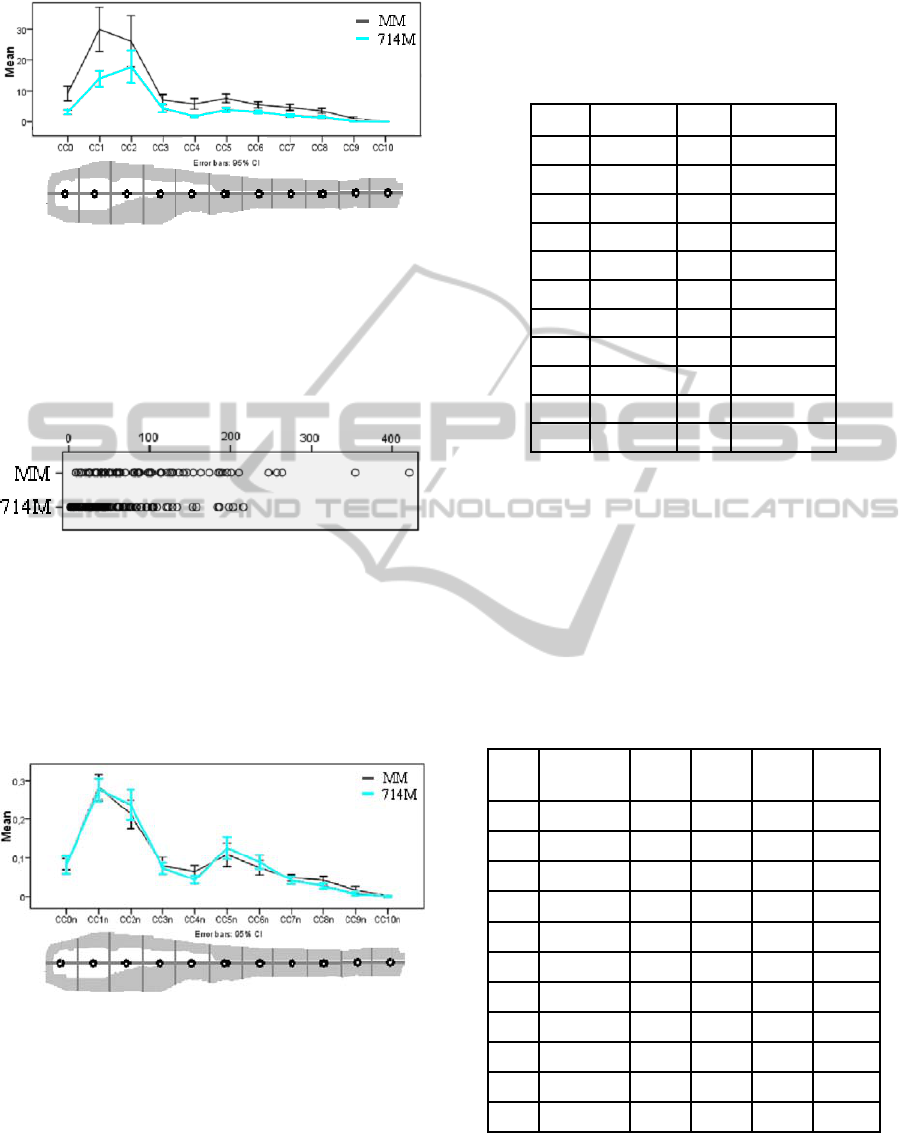
Figure 6: Spatial comparison of the average amount of

clusters for MM and 714M in relation to the zebrafish

template with a 95% confidence interval.

At this point this distribution is not conclusive. This

is due to the fact that the mean was taken from a

dataset with a certain scatter. We have analyzed the

scatter and the results are depicted in Figure 7.

Figure 7: Scatter plot of the amount of clusters in each

case of the test set used.

We are interested in the distribution of the

granuloma clusters and in order analyze the different

batches in the same way we normalize the CC[#]

over the total CC. The normalization is done for

each individual case and subsequently the mean is

calculated. In Figure 8 the results are depicted.

Figure 8: Spatial comparison of the normalized amount of

clusters for MM and 714M with a 95% confidence interval

as compared to the zebrafish template.

From the graph we can observe that MM and

714M have the same behavior. The mean and the

95% confidence interval suggest that the two

distributions can be considered as similar.

Our null hypothesis states that, under assumption

that the two groups are independent, their variances

are equal. We therefore, apply the Levene's Test for

Equality of Variances to the CC[i], i in range [0,10].

The results are shown in Table 2.

Table 2: Levene’s test for equality of variances for CC[i].

Part assume F Sig.

CC0 Equal var 5,836 0,017**

CC1 Equal var 1,526 0,218*

CC2 Equal var 6,834 0,010**

CC3 Equal var 0,403 0,526*

CC4 Equal var 0,431 0,512*

CC5 Equal var 1,508 0,221*

CC6 Equal var 6,545 0,011**

CC7 Equal var 4,200 0,042**

CC8 Equal var 0,483 0,488*

CC9 Equal var 4,029 0,046**

CC10 Equal var 0,192 0,662*

For zebrafish parts 1, 3, 4, 5, 8, 10 the

significance is always > 0.05 and thus the hypothesis

is accepted, the corresponding variances are equal

(marked with * in Table 2).

For parts 0, 2, 6, 7 and 9 the variances

significantly differ (marked with ** in Table 2).

Finally, we performed the independent samples t-

test. Based on the results from Levene’s test we

know which variances significantly differ; in Table 3

only the correct assumptions are listed.

Table 3: t-test for Equality of Means.

Part

assume t

Sig.

(2-t)

Mean

Diff

Std. Err

Diff

CC0 !Equal var

0,014

0,989 0,000 0,014

CC1 Equal var

0,244

0,808 0,006 0,023

CC2 !Equal var

-0,909

0,365 -0,024 0,027

CC3 Equal var

0,417

0,677 0,005 0,013

CC4 Equal var

2,216

0,028* 0,020 0,009

CC5 Equal var

-0,844

0,400 -0,018 0,022

CC6 !Equal var

-1,225

0,222 -0,015 0,013

CC7 !Equal var

0,815

0,416 0,005 0,007

CC8 Equal var

2,093

0,038* 0,013 0,006

CC9 !Equal var

1,603

0,112 0,008 0,005

CC10 Equal var

0,270

0,787 0,000 0,001

We observe that there is a significant difference

(this means significance < 0.05) in the mean value

for parts 4 and 8 (marked with * in Table 3).

Preliminary conclusions are as follows. In the

head the largest percentage of clusters is found,

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

260

followed by the injection site. Globally the

distribution is the same for both the MM and the

714M. Exceptions are part 4, adjacent to the

injection site, and part 8 where a significant larger

distribution of the MM bacteria is found compared

to 714M.

3.2 Distribution of the Amount of

Infection

Next, we analyze the relation between mutant and

wild type in the area covered by granulomas (cf.

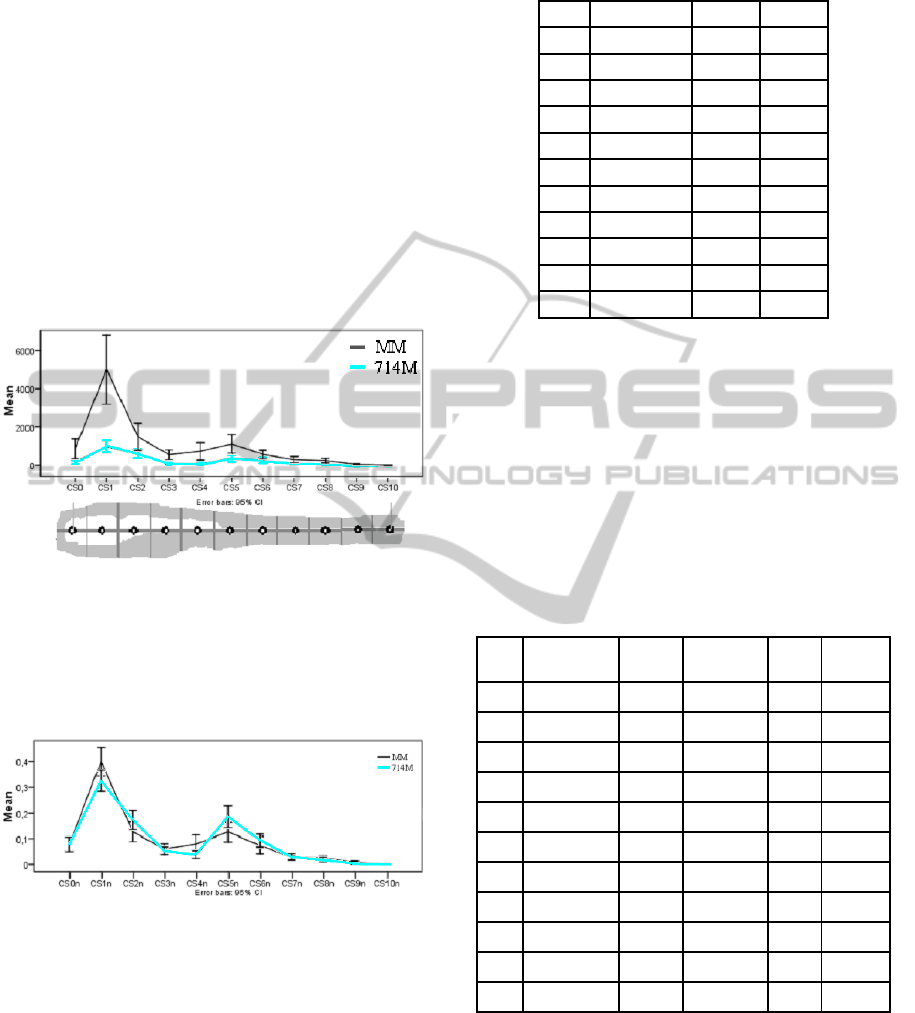
CS[#]). In Figure 9 a graph, with 95% confidence, is

depicted of the comparison of the average area of

infection between MM and 714M.

Figure 9: Spatial comparison of the average total cluster

size for MM and 714M in comparison to the zebrafish

template.

Again, as with the cluster count, we normalize the

CS[i] over the total CS for both MM and 714M and

compare the results in Figure 10.

Figure 10: Spatial comparison of the normalized average

total cluster size for MM and 714M.

From the graph in Figure 10 it seems the mean

and the distribution is similar for some parts and

very different for others; i.e. 1, 4, 5 seems to have a

very different mean. Again, our null hypothesis

states that, under assumption that the two groups are

independent, the variances are equal. We apply the

Levene's Test for Equality of Variances to the CS[i],

with i in range [0,10]. The results are shown in

Table 4.

Table 4: Levene’s test for equality of variances for CS[i].

Part assume F Sig.

CS0 Equal var 1,245 0,266*

CS1 Equal var 0,060 0,807*

CS2 Equal var 5,108 0,025**

CS3 Equal var 0,159 0,690*

CS4 Equal var 12,545 0,001**

CS5 Equal var 10,019 0,002**

CS6 Equal var 0,750 0,388*

CS7 Equal var 1,306 0,255*

CS8 Equal var 0,014 0,907*

CS9 Equal var 4,466 0,036*

CS10 Equal var 1,202 0,274*

For parts 0, 1, 3, 6, 7, 8, 9,10 the significance

> 0.05 and thus our hypothesis is accepted. The

variances marked with * in Table 4 are equal and the

variances marked with ** are different. In Figure 10,

the differences in the mean seem considerable

though the variances for MM and 714M remains the

same.

To determine the difference of the mean values

we use the knowledge gained from the Levene’s test

to do the independent samples t-test. The results are

shown in Table 5.

Table 5: t-test for Equality of Means.

Part assume t Sig. (2-t)

Mean

Diff

Std. Err

Diff

CS0

Equal var

0,016 0,987 0,000 0,021

CS1

Equal var

2,065 0,040* 0,073 0,035

CS2

!Equal var

-1,739 0,084 -0,046 0,027

CS3

Equal var

0,517 0,606 0,006 0,012

CS4

!Equal var

2,176 0,032* 0,041 0,019

CS5

!Equal var

-2,102 0,037* -0,060 0,029

CS6

Equal var

-0,850 0,397 -0,018 0,022

CS7

Equal var

-0,305 0,761 -0,003 0,009

CS8

Equal var

0,558 0,578 0,004 0,007

CS9

Equal var

1,443 0,151 0,004 0,003

CS10

Equal var

-0,528 0,598 0,000 0,001

We observe there is a significant difference in

the mean value for parts 1, 4 and 5 (marked with * in

Table 5). This result is in correspondence with initial

observation of Figure 10 in which these means

seemed rather different.

The preliminary conclusions from these findings

are the following.

NUMERICAL ANALYSIS OF IMAGE BASED HIGH THROUGHPUT ZEBRAFISH INFECTION SCREENS -

Matching Meaning with Data

261

The larger part of the infection migrates towards

the head of the zebrafish. The second large part of

infection, however, remains at the injection site. In

wild type infected fish (MM), a larger percentage of

bacteria is located in the head compared to the 714M

mutant; i.e. significant difference of the mean while

the variance is equal.

4 CONCLUSIONS

We have used a novel framework for automated

granuloma cluster recognition in order to analyze the

spatial distribution in zebrafish larvae.

As a proof of concept we have analyzed the data

for the zebrafish larva infected with the wild type

Mycobacterium marinum and one of its mutants

(714M).

From a statistical analysis of the data we can

derive information on the spread of granuloma.

More granuloma clusters are found in the

Mycobacterium marinum infected fish. However, if

we look at the normalized spread of infection it

behaves approximately the same; it either stays at

the site of injection or it moves towards the head of

the larva. For the Mycobacterium marinum it seems

that the infection is likely to migrate towards the

head compared to the 714 mutant; in the 714 mutant

it is established that the majority of the infection

stays at the injection site.

The percentage of the amount of clusters is

distributed approximately in the same way for both

test groups.

In the near future this approach will be further

elaborated with more mutants and larger dataset.

Moreover, other measurement parameters will be

considered in the analysis. Large volumes of

analysis data will allow doing predictions from the

measurements using machine learning approaches.

ACKNOWLEDGEMENTS

This work was supported by the Smartmix Program.

REFERENCES

Cootes, T. F., Taylor, C. J., Lanitis, A., 1994. Active

Shape Models: Evaluation of a Multiresolution

Method for Improving Image Searches. In

Proceedings of the British Machine Vision

Conference, vol. 1.

Cosma, C. L., Swaim, L. E., Volkman, H., Ramakrishnan,

L. and Davis, J. M. 2006. Zebrafish and Frog Models

of Mycobacterium marinum Infection. In Current

Protocols in Microbiology.

Felzenszwalb, P, 2003. Representation and Detection of

Deformable Shapes. In cvpr, vol. 1, pp.102, 2003

IEEE Computer Society Conference on Computer

Vision and Pattern Recognition (CVPR '03) - Vol 1.

Jain, A. K, Zhong, Y., Dubuisson-Jolly, M., 1998.

Deformable Template Models: a Review. In Signal

Processing - Special issue on deformable models and

techniques for image and signal, Elsevier.

Nezhinsky, A. E., Verbeek, F. J. 2010. Pattern recognition

for high throughput zebrafish imaging using genetic

algorithm optimization. In: 5th IAPR Conference on

Pattern Recognition in BioInformatics, Lecture Notes

in Bioinformatics 6282: 302-312, Springer

Nezhinsky, A. E., Verbeek, F. J. Localization and

straightening of biological shapes using a deformable

template approach. Submitted.

Volkman H. E., Clay H., Beery D., Chang J. C. W.,

Sherman D. R., et al., 2004. Tuberculous Granuloma

Formation Is Enhanced by a Mycobacterium Virulence

Determinant. In PLoS Biol 2(11).

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

262