PREDICTION MODEL OF INPATIENT MORTALITY FOR

PATIENTS WITH MYOCARDIAL INFARCTION

Hynek Kružík

, Jiří Vomlel

, Václav Kratochvíl

, Petr Tůma

and Petr Somol

GNOMON Healthcare Solutions s.r.o., Faltysova 1500/18, Prague, Czech Republic

Institute of Information Theory and Automation, Academy of Science of the Czech Republic, Prague, Czech Republic

Keywords: Data mining, Machine learning, Artificial intelligence, Logistic regression, Predictive model, Acute

myocardial infarction.

Abstract: We propose and investigate a prediction model of inpatient mortality for patients with myocardial

infarction. The model is based on complex clinical data from a hospital information system used in the

Czech Republic. The prediction of the outcome is an important risk-adjustment factor for objective

measurement of the quality of healthcare; thus it is a very important factor in healthcare quality assessment.

For our experiments we studied hospital mortality in acute myocardial infarction, because: (1) this indicator

is reliably detectable from available data; (2) treatment of acute myocardial infarction has a significant

socio-economic impact; and (3) the prediction of mortality based on admission findings is the subject of

many research papers and thus, we have a good benchmark for our experimental results. We considered

only variables that convey information about the patient at the time of admission. We selected 21 out of 637

variables and used them as predictors in logistic regression to form a prediction model for hospital

mortality. The achieved prediction accuracy was 85% and the size of the area under the ROC curve was

0.802. The results are based on a relatively small data sample of 486 patient records. Our future work will

aim at increasing the accuracy by using a larger data set.

1 INTRODUCTION

The results of medical treatment depend not only on

appropriate selection and proper execution of the

treatment, but also on initial individual conditions of

the patient. Evaluation of the patient’s initial

conditions is applicable in two major tasks: (1) in

estimating the prognosis of the patient in order to

select the most efficient treatment, e.g., the selection

of an adequate mix of interventions and medications,

or to decide on timely referral to the facility with

higher or (less commonly) lower specialization, i.e.,

for risk stratification, (2) for the retrospective

statistical evaluation of the care using standardized

quality indicators, i.e., for the risk adjustment task.

Conceptually, these two processes must be

mutually consistent. Risk adjustment of the outcome

quality indicators is essentially based on the

stratification of the risks and on empirical

knowledge and scientific evidence of the influence

which each patient's individual risk factors have on

the result of care in the group of patients.

In practice, there are significant differences in

performing risk stratification and risk adjustment

(standardization). Risk stratification is done in real

time by physicians and it is based on all available

information while standardization of the risks is

done retrospectively, mostly by medical or

regulatory authorities. During risk stratification of a

particular patient, all relevant information is

available or can be relatively easily obtained from

the clinical documentation or from additional

medical investigation. Retrospective evaluation of

the quality of outcomes is subject to many

restrictions: e.g., missing values of the variables

cannot be completed; evaluation is mostly done

outside of the healthcare facility and is based on

limited sets of available data which have not

necessarily been designed for the purpose of quality

measurement. These data sets are in general denoted

as “administrative” and the models based on them

are generally called “administrative” models.

Administrative data, i.e., demographic data,

diagnoses, procedure codes, and coded results of

hospitalization case outcomes are part of an inpatient

service reimbursement form which is utilized for all

inpatient cases reimbursed from the mandatory

453

Kružík H., Vomlel J., Kratochvíl V., T˚uma P. and Somol P..

PREDICTION MODEL OF INPATIENT MORTALITY FOR PATIENTS WITH MYOCARDIAL INFARCTION.

DOI: 10.5220/0003873504530458

In Proceedings of the International Conference on Health Informatics (HEALTHINF-2012), pages 453-458

ISBN: 978-989-8425-88-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

healthcare insurance scheme in the Czech Republic.

Differentiation of positive or negative results as

they relate to quality of service is crucial for

efficient allocation of funds; as such it is (or should

be) of primary interest to the insurance companies.

In order to create and validate an administrative

prediction model, a clinical model, i.e., risk-adjusted

clinical model, should be built first as a “gold

standard”.

For our experiments with risk-adjusted clinical

models we chose hospital mortality in acute

myocardial infarction, because: (1) this indicator is

reliably detectable from available data; (2) treatment

of acute myocardial infarction has a significant

socio-economic impact; (3) prediction of mortality

based on admission findings is the subject of many

research papers, thus we have a good benchmark for

our experimental results; and (4) no outcome-

prediction models are currently used in the Czech

Republic; thus they are a necessary novelty in

quality measurement.

Our work has been motivated by the work

published at the Yale University (Krumholz, H. M.,

et al, 2007).

2 METHODS

2.1 Risk Adjustment

Risk adjustment is a statistical process used to

identify and adjust for variations in patient outcomes

that stem from differences in patient characteristics

(or risk factors) across healthcare organizations in

order to achieve better comparison of patient

outcomes between different organizations and to

improve the interpretability of results. The quality of

healthcare can be measured by several types of

indicators: by mortality, by re-hospitalization rate or

by complication rate. In this part, we will show

reasons and principles of risk adjustment of a

mortality indicator. Standardization of other types of

indicators follows the same principles.

A straightforward comparison of mortality rate

of two different healthcare facilities will not give

objective results as it also depends on the presence

of risk factors at the time of health care encounters.

Patients may experience different outcomes

regardless of the quality of care provided by the

healthcare organization, so comparing patient

outcomes across healthcare organizations without an

appropriate risk adjustment could be misleading. By

adjusting for the risks associated with outcomes of

interest, risk adjustment facilitates a fairer and more

accurate inter-organizational comparison. (CMS,

2005).

There are two essential methods: (1) case

stratification, i.e., decomposition of cases into more

homogeneous sub-groups based, for example, on age

and/or sex grouping, or (2) standardization of results

(indicators), i.e., risk-adjustment. The first method,

however, is disadvantageous both in terms of

statistics (subgroups will often have small numbers

of patients) and in terms of subsequent interpretation

(different subgroups may have different comparative

results and it may not be clear how the provider

should actually be evaluated with respect to the

overall quality in the clinical area).

2.2 Selection of Risk Factors

The requirements for the selection of risk factors

applicable in the standardization process indicators

are as follows: (i) there must be a statistically

significant relationship between risk factor and the

outcome indicator. For example, if the probability of

death from myocardial infarction is related to the

value of blood pressure at the time of admission,

then it is included as a risk factor. The prediction

model should also reflect situations in which certain

combinations of factors have greater impact than

each of the individual factors alone; (ii) the

composition of patients, in terms of risk factors,

must be different in different healthcare facilities.

Otherwise, there is no need to carry out

standardization, although there is a strong

correlation between the indicator and risk factor – all

healthcare facilities are "disadvantaged" in the same

way. In practice, this requirement is usually met, as

healthcare facilities usually have different

distributions of risk factors among their patients; (iii)

each risk factor must clearly reflect the condition of

the patient upon admission to a healthcare facility

and may not be the result of the treatment process

itself; (iv) each risk factor has to be reliably

documented within the available data –

unfortunately, this is a very limiting restriction in

many cases, and especially in administrative data.

It is obvious that the correction of the

measurement bias is never perfect. Even after

standardization, residual bias remains. Residual

distortion can, for example, be caused by risk factors

that are not yet known or that are not reflected in the

data.

2.3 Standardization of Indicators

When standardizing the quality indicators it is first

HEALTHINF 2012 - International Conference on Health Informatics

454

necessary to find and express the relationship

between the indicator and each risk factor. Suppose

that the risk factor is age and the outcome indicator

is the hospital mortality of acute myocardial

infarction. Based on data from the entire set of

healthcare facilities (standard population) it is

therefore necessary to express, with the help of

statistical methods, the relationship between the

patient's age and the likelihood of death from heart

attack. Then, for each hospital the correlation index

(CI) is calculated. CI is defined as the proportion of

two variables: the actual number of deaths and the

predicted (expected) deaths: CI = the actual number

of deaths / predicted (expected) number of deaths.

The expected number of deaths in a hospital is

the sum of individual probabilities of death of all

patients admitted to the hospital, determined with

respect to their risk factors. The expected number of

deaths is the number of deaths that would be

expected if the hospital held the same mortality risk

as the population of all hospitals. If the actual

number of deaths differs from the expected number,

we can conclude there are internal factors that have

an influence on the number of deaths in this

particular hospital. The correlation index is a

dimensionless number that indicates the relative

position of the hospital compared with the average:

an index value greater than one indicates above

average mortality, while an index value less than one

indicates the contrary, i.e., below average mortality.

Standardized mortality rate is obtained by

multiplying the index value by general mortality,

i.e., the average mortality for all hospitals:

standardized mortality = general mortality * CI.

The result of standardization of the indicator is

the value of the indicator on the condition that the

hospital had the same distribution of risk factors as

the entire group of providers.

2.4 Patient Sample

Our initial study is comprised of cases from one

Czech hospital. After exclusion of patients

transferred for treatment elsewhere, we selected all

patients admitted to the hospital with the main

diagnosis of acute myocardial infarction (ICD-10

codes in the range of I210 - I214). Our resulting data

set consisted of 486 patients (both male and female,

without age restrictions). The data set includes the

usual demographic and administrative data including

outcome status, principle and secondary diagnoses

coded using ICD-10, list of procedures coded using

the Czech national list of medical procedures, and

laboratory results. In addition, we had complete

information about previous hospitalizations in the

same hospital during the 12 months prior to the

respective hospitalization. In total we considered

637 variables (possible risk factors). Only 151

patient records included all values of the potential

risk factors. Patient records with missing values

were not excluded; instead, to keep maximum usable

information, we used a method of imputation of

missing data values (Rubin, D. B., 1987).

2.5 Statistical Analysis

The first and most difficult step in the

standardization of a selected indicator is to identify

relevant risk factors and formally characterize their

influence on the selected indicator. Often (see, e.g.,

Krumholz et al, 2007) the relationship between the

risk factors and the selected indicator is expressed

using logistic regression.

Let P(Y = 1|X=x) denotes the probability that the

variable Y reaches the value 1 given the value x of

the vector of risk factors X. In our case it is the

probability that the patient will die within 30 days

after admission to the hospital.

The logistic regression model defines the

relationship between the dependent variable  and a

vector of the risk factors  having values of

vector . The relationship is defined by the logistic

function

(

=1|=

)

exp

(

′

)

1+exp

(

′

)

(1)

where  is the vector of parameters to be found and



′

denotes its transposition. Vector  is usually of

the form

(

1,

)

and the first component of vector ,

referred to as 



, is the absolute member (intercept).

First, we selected candidates for the risk factors

based on the information gain method. Information

gain of each risk factor  and the dependent variable

 is defined as



(

,

)

=

(



)

+

(



)

− (,) ,

(2)

where 

(



)

is the entropy of variable  defined as



(



)

=−(=)log(=)



(3)

and (,) is the mutual entropy of variables  and

 defined similarly as



(

,

)

=−

(

=,=

)

,

log

(

=,=

)

(4)

Log is the binary logarithm. The higher the

information gain, the more information variable 

PREDICTION MODEL OF INPATIENT MORTALITY FOR PATIENTS WITH MYOCARDIAL INFARCTION

455

brings about the value of variable . Absolute values

of laboratory tests have been used, not relative

values against the standard range for age and sex of

the patient. Values of continuous variables were

divided into ten bins for the purpose of information

gain calculations. For further processing, we ranked

only variables whose information gain was greater

than 0.01. The finally selected variables are given in

Table 1.

Table 1: Variables with an information gain greater than

0.01.

Code Description Information

gain

Urea Serum urea 0.11674202

Crea Serum creatinine 0.09532763

Leuco Leukocytes in full blood 0.06820710

I48 Atrial fibrillation and flutter 0.02425088

O.E78 Disorders of lipoprotein

metabolism and other

lipidaemias

0.02318073

O.I20 Angina pectoris 0.02044021

O.I48 Atrial fibrillation and flutter 0.01997538

I73 Other peripheral vascular

diseases

0.01971532

O.I27 Other pulmonary heart

diseases

0.01971532

O.I73 Other peripheral vascular

diseases

0.01971532

Age Patient’s age 0.01926587

O.I46 Cardiac arrest 0.01851840

K92 Other diseases of digestive

system

0.01758336

O.I21.0 Acute transmural myocardial

infarction of anterior wall

0.01651995

I74 Arterial embolism and

thrombosis

0.01576957

I42 Cardiomyopathy 0.01474711

O.I42 Cardiomyopathy 0.01474711

O.I10 Essential (primary)

hypertension

0.01471863

O.I21.1 Acute transmural myocardial

infarction of inferior wall

0.01440448

O.I64 Stroke, not specified as

haemorrhage or infarction

0.01358037

I27 Other pulmonary heart

diseases

0.01349612

K29 Gastritis and duodenitis 0.01338366

K62 Other diseases of anus and

rectum

0.01290232

L95 Vasculitis limited to skin, not

elsewhere classified

0.01290232

K57 Diverticular disease of

intestine

0.01217010

I50 Heart failure 0.01158408

O.I21.4 Acute subendocardial

myocardial infarction

0.01140944

K80 Cholelithiasis 0.01054740

Variables prefixed with "O" indicate diagnoses

that the patient encountered during the examined

hospitalization. Other diagnoses (without the "O"

prefix) were taken from the patient's hospitalizations

within one year prior to the hospitalization studied.

Variables in Table 1 were then used for training

the logistic regression model. For this purpose the

values of all the considered variables were

normalized to the interval <0, 1>. Some patients did

not have all selected variables examined. One option

for such patients was their exclusion from the data

set. This would, however, significantly reduce the

available data. Therefore, we chose Multivariate

Imputations by Chained Equations (cf. Rubin, D. B.,

1987 or Buuren, S., at al, 2006) to substitute the

missing values. Alternatively, we also tested the

replacement of missing risk factor values by the

average value of this factor, but in this case the

results proved to be less accurate. We also excluded

variables that were causing singularities: O.I73,

O.I42 and L95, and also those that might yield

misleading information due to co-morbidities: O.I20,

O.I48, O.I46 and O. I64.

For the actual learning of the model parameters

of logistic regression we have used the glm module,

which is part of the statistical system R (R

Development Core Team, 2010).

3 RESULTS

The resulting model is described in Table 2. The

first column includes the names of the risk factors as

in Table 1.

In the second column there are individual

coefficients , i.e., the components of vector  of

the logistic regression formula. Standard deviations

of the coefficient are in the third column, and the

fourth column contains the corresponding values of

 Student's t-test -- i.e., whether coefficient  has the

given mean value. The fifth column shows the

number of degrees of freedom of the Student's t-

distribution calculated in accordance with (Barnard

and Rubin, 1999). The last column gives the

probability of alternative hypotheses of the t-test

presented. Values lower than 0.05, which

corresponds to the static level of significance of 5%,

are shown in bold. These values indicate that the

hypothesis that coefficient β has the given value as

its mean value is accepted at a static level of

significance of 5%.

The values of coefficients β thus can be roughly

interpreted as follows: the greater a positive number,

the greater the influence of the corresponding risk

factor on the probability of death. The lower a

negative number, the greater the influence of the

corresponding risk factor on the probability of

HEALTHINF 2012 - International Conference on Health Informatics

456

Table 2: Parameters of the logistic regression model.

Code



SD t value degrees of

freedom

Alt. hyp.

(Intercept) -2.1060975 1.2651842 -1.664656859 31.598080 0.105868127

Urea

8.6381220 3.2418691 2.664549922 6.539030 0.034363798

Crea -1.0298399 3.1864171 -0.323196842 6.948143 0.756055460

Leuco 1.3401639 2.5917890 0.517080649 6.072126 0.623388122

I48

1.1774437 0.5043932 2.334376623 62.932775 0.022781215

O.E78

-1.1969985 0.4437995 -2.697160631 456.217585 0.007252314

I73 24.2072289 3127.7478688 0.007739508 463.999987 0.993828154

O.I27 22.4904111 3055.1132840 0.007361564 463.999942 0.994129539

Age -0.8665293 1.2988153 -0.667169004 46.748401 0.507944173

K92 0.1754608 2.1248919 0.082573969 260.797168 0.934253641

O.I21.0 2.0831447 1.2175409 1.710944339 14.713859 0.108083943

I74 0.8435731 1.2306952 0.685444349 363.623078 0.493500307

I42 18.6880782 3580.0597075 0.005220047 463.999856 0.995837268

O.I10

-1.7197621 0.5011027 -3.431955378 32.644378 0.001645515

O.I21.1 -18.4366694 1142.1321492 -0.016142326 463.999889 0.987127785

I27 -0.3723272 2.1099515 -0.176462425 220.553439 0.860092594

K29 -0.6493484 1.1797607 -0.550406839 49.675659 0.584507085

K62 1.6111716 3.1727303 0.507818643 83.887081 0.612913195

K57 1.5036105 1.8285737 0.822285931 17.330469 0.422084093

I50 -0.2095659 0.5698730 -0.367741513 18.221241 0.717302894

O.I21.4 -0.2596627 1.1148068 -0.232921682 9.406510 0.820811800

K80

1.4525334 0.5681741 2.556493236 388.428873 0.010952816

survival. The number in the last column tells us to

what extent this effect is statistically significant. For

values greater than 0.05 (which is true for most of

our risk factors), we can say that the impact on the

probability of death was not statistically proven in

our data set. However, it is necessary to remark that

these results are affected by the small number of

patients in our data set.

3.1 Evaluation of Results of the

Logistic Model

For a reliable evaluation of the quality of the trained

prediction model, independent data that were not

used to learn the model are needed. For this purpose

we used the method of K-fold cross-validation,

where K had a value of ten. We randomly divided

the data set into ten groups of approximately equal

size. The remaining nine groups were used to train

the model which was then validated on the selected

group. This procedure was repeated for each of the

ten groups. The results presented below summarize

all partial results.

The basis for evaluation is the confusion matrix,

which includes numbers of true positive (tp) and

false positive (fp) predictions that the patient will die

and true negative (tn) and false negative (fn)

predictions that the patient will not die.

The results of our model were as follows: tp =

28, tn = 383, fp = 9, fn = 66. Based on these values

we can express the results of model evaluation:

accuracy = 0.85, precision = 0.76, recall =

0.30, and false alarm rate = 0.02.

The output of the logistic regression model is not

only an estimate of whether or not the patient dies

within 30 days, but it gives the probability with

which this event occurs. Also, it is possible to

change the decision threshold (which is normally set

to 0.5) of the classification. This enables us, for

example, to increase recall at the expense of

precision and vice versa. The overall behavior of

such a classifier is best characterized by the ROC

curve, see Figure 1.

The ROC curve shows the dependence of recall

and false alarm rate on the value of the threshold

(threshold values are shown below the curve in

Figure 1). The higher the curve is located, the better

results the model gives. A good measure of

classifier’s performance is the size of the area under

the curve, i.e., the ROC area. The maximum value

that represents the ideal classifier is 1.0. On the

contrary, a value of 0.5 can be reached by a random

classifier. The value of the ROC area of our model

was 0.802.

PREDICTION MODEL OF INPATIENT MORTALITY FOR PATIENTS WITH MYOCARDIAL INFARCTION

457

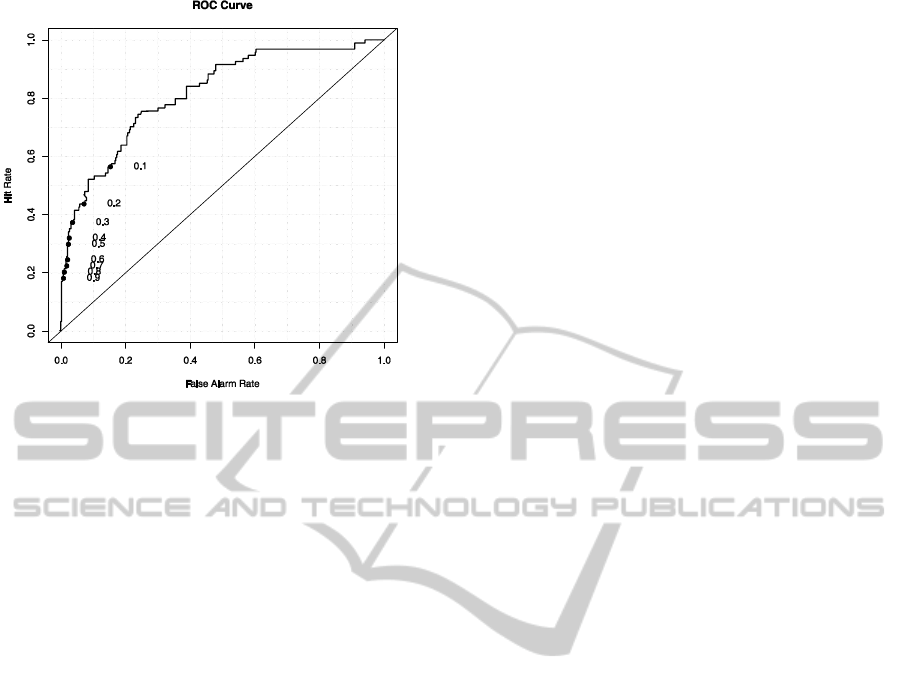
Figure 1: ROC curve of the classifier.

4 CONCLUSIONS

In this work we studied the standardization of

outcome indicator “hospital mortality in acute

myocardial infarction.” Although we had a relatively

small data sample and we used only the main and

secondary diagnoses and the results of three

laboratory tests to build a predictive model, we

succeeded in predicting the 30-day mortality of

patients relatively successfully. The achieved

accuracy was 85% and the size of the area under the

ROC curve was 0.802. With regard to the statistical

properties of predictive models of this type, it can be

expected that a better prediction could be achieved

by using other data from an electronic patient record,

such as ECG, localization of pain and blood pressure

(these data are stored only in free text format and

would involve difficult pre-processing to enable us

to use them in the classifier construction; this was

beyond the scope of this paper). For practical use of

our result in the standardization of mortality

indicators, it will be necessary to train the model

using a larger data set from many hospitals. Then it

will also be possible to make a better medical

interpretation of the achieved results.

Another challenge, which we intend to address in

the future, is researching the effect of a combination

of several risk factors and the use of ratings of

laboratory test results performed with respect to the

normal ranges for a particular sex and age

combination, rather than with respect to their

nominal values only.

ACKNOWLEDGEMENTS

This work was carried out under the grant of the

Ministry of Education of the Czech Republic No.

2C06019, ZIMOLEZ.

REFERENCES

CMS, 2005. Specification Manual for National Hospital

Quality Measures, version 1.0., http://qualitynet.org.

Krumholz, H. M., et al., 2007. Risk-Adjustment Models

for AMI and HF 30-Day Mortality, Methodology.

Harvard Medical School, Department of Health Care

Policy.

Rubin, D. B., 1987. Multiple Imputation for Nonresponse

in Surveys. John Wiley and Sons, New York.

Buuren, S. et al., 2006. Fully conditional specification in

multivariate imputation. Journal of Statistical

Computation and Simulation, 76, 12, 1049–1064.

Barnard, J., Rubin, D. B., 1999. Small sample degrees of

freedom with multiple imputation. Biometrika, 86,

948-955.

R Development Core Team, 2010, R: A Language and

Environment for Statistical Computing. R Foundation

for Statistical Computing, Vienna, Austria, ISBN 3-

900051-07-0, http://www.R-project.org

HEALTHINF 2012 - International Conference on Health Informatics

458