
A METHOD FOR SPECIFYING SEMANTICS OF LARGE SETS
OF 3D MODELS
Xin Zhang
1
, Tim Tutenel
2
, Rong Mo
1
, Rafael Bidarra
2
and Willem F. Bronsvoort
2
1
Northwestern Polytechnical University, Xi'an, China
2
Computer Graphics Group, Delft University of Technology, Delft, The Netherlands
Keywords: Model Classification, Segmentation, Annotation, Semantics.
Abstract: Semantics of 3D models is playing a crucial role in games and simulations. In this paper we propose a
framework to specify semantics of large sets of 3D models with minimal human involvement. The
framework consists of three modules: classification, segmentation and annotation. We associate a few
models with tags representing their classes and classify the other models automatically. Once all models
have been classified in different groups, we take a certain number of models as template models in each
group, and segment these template models interactively. We then use the segmentation method (and
parameters) of the template models to segment the rest of the models of the same group automatically. We
annotate the interactively segmented parts and use an attributed adjacency graph to represent them.
Automatic annotation of the rest of the models is then performed by subgraph matching. Experiments show
that the proposed framework can effectively specify semantics of large sets of 3D models.
1 INTRODUCTION
With rapid advancements in modeling techniques
and graphics hardware, very complex and visually
convincing 3D models become more important in
virtual worlds. In recent years, quite some research
has been done on semantics of models, to make
them behave more as in real-life. Semantics of
models is all information about the model, in
addition to its geometry (Bronsvoort et al., 2010).
This can include various parameters, e.g. for
physical properties, roles, behavior and services they
provide. Semantic information of models can be
useful in many applications: 1) by using semantic
models when generating virtual worlds
automatically, the output can be improved (for
example, information about placement relationships
can create more realistic layouts (Tutenel et al.,
2009)); 2) detailed and extensive information about
object interaction, and services provided by objects,
can lead to more immersive and compelling
gameplay experiences (Kessing et al., 2009); and 3)
behavioral information can be used to maintain
semantic consistency in adaptive environments.
More on the role semantics can play in virtual
worlds can be found in (Tutenel et al., 2008).
However, specifying semantics of 3D models is
often a laborious and repetitive task. It is therefore
important to find techniques to assist a user in this
task. Semantics of 3D models can generally be
divided into two categories: global semantics and
local semantics. Global semantics describes general
information about 3D models, including their names,
materials, volumes and relationships with other
models. Local semantics describes information on
the individual parts of which the model is composed,
and relationships among these parts. To our
knowledge, most current methods specify semantics
of 3D models manually or semi-automatically, and
usually the semi-automatic methods still require a
great deal of user interaction. Our method tries to
reduce the amount of interaction. For specifying
global semantics, some methods propose to classify
the 3D models and use the semantics of already
classified models to annotate the unknown ones if
they are in same group. However, due to the
mismatch between the high-level human intention
and the low-level geometric data representation,
usually called the “semantic gap” (Smeulder et al.,
2000), the results of automatic classification are not
convincing. For specifying local semantics, we need
to segment 3D models into meaningful parts and
97
Zhang X., Tutenel T., Mo R., Bidarra R. and F. Bronsvoort W..
A METHOD FOR SPECIFYING SEMANTICS OF LARGE SETS OF 3D MODELS.
DOI: 10.5220/0003885500970106
In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 97-106
ISBN: 978-989-8565-02-0
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

annotate each part. The problem of segmentation of
3D models is still a challenge, because current
methods cannot automatically separate models into
meaningful parts without context.
In this paper, we propose a method for
specifying global and local semantics of 3D models
with minimal human intervention. We manually
annotate a few models with tags (global semantics)
as training models. We classify the rest of the
models based on these training models and associate
them with the tag of the training models in the same
class. After all the models have been classified, we
choose a few models as template models from each
class. The template models are segmented and the
model parts are annotated with tags (local semantics)
interactively. The segmentation method (and
parameters) of template models can be used to
partition the models with the same tag. Once the
models have been separated into parts, we rely on
Attributed Adjacency Graph (AAG) to represent the
model parts. The AAG representing the parts of a
template model contains local semantics. Therefore,
specifying the local semantics of partitioned models
can be accomplished by subgraph isomorphism. The
main contributions of this paper include: 1) A
framework for specifying semantics of 3D models
with limited human involvement; 2) The use of
subgraph isomorphism for annotation of model
parts.
The remainder of this paper is organized as
follows. In Section 2, we introduce the related work
on specifying semantics of 3D models. The outline
of our method is described in Section 3. Specifying
local semantics of 3D models is described in Section
4. Our prototype system is presented in Section 5,
and we show results and give conclusions in
Sections 6 and 7.
2 RELATED WORK
In order to classify 3D models, we need to define a
shape descriptor first, which is used to compute the
similarity between 3D models. In the past decade,
many shape descriptors have been proposed in the
scope of shape-based 3D model retrieval. Some
shape descriptors rely on geometry to compare 3D
models, such as Shape distribution (Osada et al.,
2002), Spherical harmonic (Saupe and Vranic, 2001)
and 3D Zernike (Novotni and Klein, 2004)). Reeb
graph (Biasotti et al., 2008) is based on topology. A
more general overview of shape descriptor can be
found in the survey (Tangelder and Veltkamp,
2004). Despite of years of research, the retrieval
performances of above-mentioned methods are very
limited. Once the shape descriptor for computing the
similarity between models has been determined, we
can resort to several methods to classify the models,
such K-NN (Han and Karypis, 2000), SVM
(Novotni et al., 2005), and neural networks
(Carpenter and Hoffman, 1997).
All approaches described above use geometry or
topology to compute the similarity between 3D
models. Actually, some models are similar in shape,
but they are not similar at all when looking at their
meaning, because of the semantic gap. For example,
in Fig. 1, the models “Bottle” and “Balloon vehicle”
are similar in shape, but they are quite different
objects. Relevance feedback is often used to bridge
the semantic gap. The most important part of
relevance feedback is the learning algorithm. Some
approaches (Rocchio, 1971) modify query vectors or
change the weight of elements of the vector to make
it move towards positive and away from negative
examples. Other methods (Giacinto and Roli, 2004)
use a Bayesian framework to estimate the posteriori
probability after each iteration. Recently, several
kinds of SVM (Novotni et al., 2005) with different
kernels have been successfully utilized in
classification and relevance feedback due to its
efficiency and precision.
Figure 1: 3D Model “Bottle” and “Balloon vehicle”.
The two main tasks in specifying local semantics
of model parts are segmentation and annotation.
Many methods employing geometric criteria for
model segmentation were proposed in the last
decade, including Region growing (Pavlidis and
Liow, 1990), Fitting primitives (Attene et al., 2006),
Random walks (Lai et al., 2008), Random cuts
(Golovinskiy and Funkhouser, 2008), Reeb graph
(Biasotti et al., 2008)) and Shape diameter (Shapira
et al., 2008). A recent survey can be found in (Chen
et al., 2009). These methods make use of curvature,
normal direction, geodesic distance or volume for
segmentation. However, approaches using pure
geometric attributes hardly produce meaningful
model parts for annotation (Attene et al., 2009).
Therefore, such methods usually need manually
tuned parameters to get satisfactory and consistent
Bottle Balloon vehicle
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
98
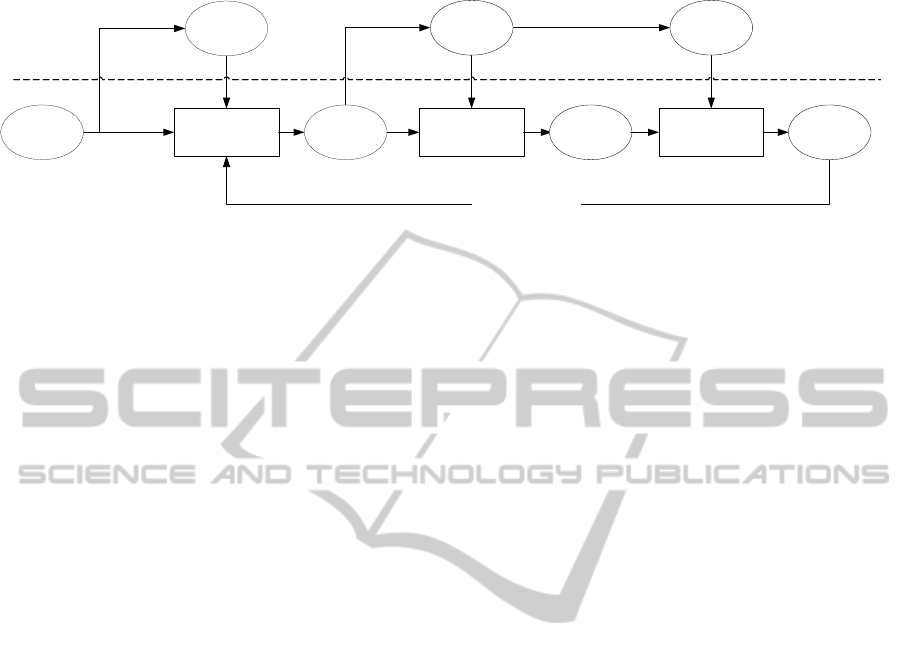
Figure 2: The framework of our method for specifying semantics of 3D models.
results. Once 3D models have been segmented, some
methods (Attene et al., 2009 and Robbiano et al.,
2007), use well-defined tag dictionaries to annotate
model parts manually. The papers about these
methods also point out that automatic annotation of
model parts could be done by exploiting topologic
and geometric properties of parts, but they do not
give a concrete way for such automatic annotation.
Recently, a few approaches combined 3D model
segmentation and labeling with recognition of model
shape; they are inspired by image segmentation in
computer vision (Tu et al., 2005, and Schnitman et
al., 2006). One such method (Golovingskiy and
Funkhouser, 2009) simultaneously segments 3D
models by matching points among a set of models.
This method can segment 3D models in a class
consistently, and transfer labels based on matches.
However, the method needs all 3D models to be
classified first, and it is not suitable for large sets of
3D models: it needs to consider each pair of models
for correspondences. Another method (Kalogerakis
et al., 2010) learns a large variety of geometric and
contextual label features from a collection of labeled
training models, and uses these label features to
segment models and label model parts automatically.
This method achieved a significant improvement
compared with current segmentation methods.
However, it requires consistently labeled models for
training, and the performance typically drops with
fewer training models, because it combines multiple
geometric attributes and needs to determine which
attributes are distinguished for certain types of
models in the learning process. Our method to
specify semantics of 3D models also combines
segmentation with recognition. Compared with
method (Kalogerakis et al., 2010), our method needs
much less training models because we rely on
subgraph matching to annotate model parts. Another
advantage of our method is that the framework can
easily incorporate other, better segmentation
methods, and thus improve the results of
specification of semantics.
3 FRAMEWORK OF THE
PROPOSED METHOD
First, we refer to 3D models without any semantics
as untagged models. Once models have been
classified into a particular class we call them tagged
models, after the segmentation we call them
partitioned models, and once their parts have been
annotated we call them specified models. The
specified models will be further used as tagged
models and improve the classification by relevance
feedback. Every relevance feedback step is an
iteration of the classification. This leads to three
major steps in the method: classification,
segmentation and annotation.
The workflow of the system is illustrated in Fig.
2. It also shows the breakup between the automatic
phase and the interactive phase: for each step, the
user needs to interactively create some training data
that will be used in the automatic phase. For
example, the user can classify one table model, after
which the method will classify all other table models
in the same class, possibly aided by the relevance
feedback. This will be further explained in the next
subsections.
3.1 Model Classification Step
In this section, we use the most popular method SH
(Saupe and Vranic, 2011) to compute the similarity
between models and SVM to classify the 3D models
due to its robustness and simplicity. In order to use
SVM to classify the models, we need to choose
appropriate training models. Training models have a
large impact on the classification result. Less
training models would result in a bad classification
result. However, too many training models need lots
of tedious work and are not suitable for large sets of
Interactive phase
Classification Segmentation Annotation
Automatic phase
Relevance feedback
Untagged
models
Tagged
models
Partitioned
models
Specified
models
Specified
models
Tagged
models
Partitioned
models
n
1
<<N
N-n
1
n
1
N
n
2
n
2
<<N
N-n
2
training models template models
A METHOD FOR SPECIFYING SEMANTICS OF LARGE SETS OF 3D MODELS
99

3D models. The best training models should spread
over all the ranges of 3D models.
Therefore, we rely on the k-means method to
cluster all the 3D models and choose several models
from each class. We assign tags from the semantic
library (Tutenel et al., 2009) to these models
manually, and use these tagged models as training
models. Then, we classify all the remaining
untagged models based on the training models and
associate these untagged models with the tag of the
tagged models in the same class. In the end, the
untagged models are specified. The specified models
are further used to improve the classification.
3.2 Model Segmentation Step
Since 3D model segmentation is out of the scope of
this paper, we rely on the currently mature methods
for model segmentation. 3D models can be generally
divided into two categories: man-made models,
having obvious boundaries, and freeform models.
Man-made models are much easier segmented
compared with freeform ones. For example, we
could simply use Region growing (Pavlidis and
Liow, 1990) to segment a man-made model into
several different parts automatically. However, this
method fails to work on freeform models. We have
to use other, more sophisticated methods, such as
SDF (Shapira et al., 2008), to cope with such
freeform models. This method usually provides
users with an interactive way of manipulating
parameters to get a correct segmentation result.
We argue that, with the global semantics
associated to 3D models, we can reduce the users’
interaction for segmentation since models with the
same tag may have the same segmentation method
and even have similar parameters of the same
method. For each group of models with the same
tag, we choose only a few template models and
segment them interactively. We use the
segmentation method (and parameters) of the
template models to partition the rest of the models in
the same group automatically.
Choosing the training models wisely is
obviously an important factor towards good
specification results. When there are a number of
different model shapes in the same class, the training
models should all be models of the same shape, but
instead reflect the variability of the shapes. A simple
example might be the table class. A set of models
might contain a number of round tables and a
number of rectangular tables. For the best result,
both round and rectangular tables need to be chosen
as training models to guarantee optimal results.
Choosing the training models wisely is
obviously an important factor towards good
specification results. If there are a number of
different model shapes in the same class, the training
models should reflect the variability of the shapes. A
simple example might be the table class. A set of
models might contain a number of round tables and
a number of rectangular tables. For the best result,
both round and rectangular tables need to be chosen
as training models.
3.3 Model Annotation Step
Once a template model has been segmented, we
annotate some model parts based on the tags from
the semantic library (Tutenel et al., 2009). An AAG
is defined to represent the annotated model parts,
where each node denotes a model part and an edge
keeps the relationships between two model parts.
The automatically partitioned models are also
represented by AAGs. We refer to the AAGs
constructed from the template models as sub-AAGs
because not all the parts of the template model are
annotated. Therefore, the automatic annotation can
be accomplished by subgraph matching, finding a
mapping between a sub-AAG and an AAG. The
details of this part are further described in the next
section.
Figure 3: Segmentation results (a) segmentation of man-
made models (b) segmentation of freeform models (c)
different parameters of segmentation for a freeform model.
4 SPECIFICATION OF LOCAL
SEMANTICS
Specification of semantics for the model parts is
composed of a segmentation step and an annotation
step. Due to the fact that there is no single
(a)
(b)
(c)
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
100

segmentation method suitable for all 3D models, we
use multiple methods for segmentation. After the
tagged models have been segmented, we resort to
AAGs to represent the partitioned models, and use
subgraph matching to annotate model parts
automatically.
4.1 Multiple Segmentation Methods
Model segmentation is a difficult field in computer
graphics. To our knowledge, there is no one method
that fits all types of 3D models. Therefore, we rely
on two mature methods for segmentation in our
system, since the segmentation of man-made models
and freeform models are quite different. For
example, some man-made models (Fig. 3 (a)), can
be automatically segmented into different model
parts by Region growing (Pavlidis and Liow, 1990).
However, this method fails to work on freeform
models (Fig. 3 (b)). We have to make use of SDF
(Shapira et al., 2008) to segment these freeform
models. Even with the SDF method, a 3D model can
be partitioned quite differently with different
parameters (Fig. 3 (c)). Therefore, we need to
determine the appropriate segmentation method and
parameters from the training models interactively,
and use this method and these parameters for
segmenting other models in the same class.
4.2 AAG Construction
After all the models have been segmented, we use
AAGs to represent the partitioned models. Suppose
a partitioned 3D model is = {
,
,⋯,
}. It
can be represented by an AAG(, ), where each
segmented part
is denoted as a node
∈; the
graph edge
,
∈ exists whenever the two
parts
,
∈ are adjacent. The node
keeps the
geometric attributes of part
, such as its volume,
surface area, main axis and number of adjacent
parts. The edge
,
keeps the relationships
between parts
and
, such as distance and
relative position (parallel or perpendicular). Two
partitioned 3D models and their related AAGs are
shown in Fig. 4.
In our system, we compute the geometric
attributes and relationships of the bounding box of a
part, rather than of the part itself, because of
efficiency and robustness. It is much faster to
compute the volumes and adjacency relationships of
bounding boxes than of the actual model parts. Most
algorithms for calculating the volume also fail to
cope with models with holes. In our experiments,
using the bounding box instead of the part itself
proved sufficient, despite the slightly decreased
precision.
The geometric attributes and relationships kept
in nodes and edges of an AAG are critical for
subgraph matching. Therefore, we need to consider
the attributes and relationships which are invariant
when the models are scaled, translated or rotated,
and even when some pose changes, such as a human
model in standing and walking poses. Volume is an
important attribute. A node with a large volume is
unlikely to match a node with a small volume.
However, the volume of a model part is not scale
invariant, and thus it needs to be normalized before
using. Adjacency relationships of model parts are
also very important for matching. In our
experiments, we consider three cases: disconnection,
connection and containment. If the bounding boxes
of two model parts do not intersect, the adjacent
relationship is disconnection. If the bounding boxes
intersect but do not contain each other, the
relationship is connection; otherwise, the
relationship is containment. Parallel or perpendicular
structures of models also help the procedure of
subgraph matching. We need to keep these
relationships in the AAG.
Figure 4: Segmented models are represented by AAG.
4.3 Subgraph Matching
We annotate the parts of template models
interactively, and keep the annotation in the nodes of
their sub-AAGs. Therefore, the automatic annotation
of the rest of the models could be done by subgraph
matching, which finds a one-to-one mapping
between nodes of a sub-AAG and an AAG.
Subgraph matching is an NP-complete problem.
The time requirements of brute force matching
algorithms increase exponentially with the size of
the input graphs. There are several available
algorithms, such as Ullmann’s method (Ullmann,
1976), SD (Schmidt and Druffel, 1976), and VF
tabletop
table leg
table leg
table leg
table leg
tabletop
table leg
table leg
table leg
table leg
table bar
table bar
table bartable bar
A METHOD FOR SPECIFYING SEMANTICS OF LARGE SETS OF 3D MODELS
101

(Cordella et al., 2001). Ullmann proposed a depth-
first search-based algorithm with refinement
procedures, which is now the most popular and
frequently used algorithm for subgraph
isomorphism. Our system also makes use of
Ullmann’s method for AAG subgraph matching and
automatic annotation. For example, in Fig. 5, if there
is a correspondence between a sub-AAG and an
AAG, we will annotate the related nodes of the
AAG as a sub-AAG.
Figure 5: Subgraph matching.
In the refinement procedures of Ullmann’s
method, the core part is to determine whether a node
of the sub-AAG corresponds to a node
of the
AAG. Suppose we have found a mapping between
=
{
,
,⋯,
}
from the sub-AAG and
={
,
,⋯,
} from the AAG, i.e., these are
isomorphic, then we need to determine whether the
next node
corresponds to
or not. We use
several criteria to judge this, e.g., we consider the
geometric attributes of nodes and relationships
between them. The pseudo code is in Algorithm 1:
Algorithm 1. Verify the paired nodes
Bool VerifyNextNodes(
,
,
,
)
//Initialization
=
{
,
,⋯,
}
,
=
{
,
,⋯,
}
for each
∈
,
∈
, =1,⋯,−1
//Begin to match
if the adjacency relationship of
and
is not equal
to that of
and
return false
if the volume ratio of
and
is not close to the
volume ratio of
and
return false
if
is parallel (perpendicular) to
if
is not parallel(perpendicular) to
return false
//Otherwise
return true
To further optimize the above algorithm, we take
advantage of prior knowledge to reduce the search
space. The details of this are described in Section
5.4. Meanwhile, the number of model parts is never
really large: less than 20 in most of our experiments,
and never more than 100 in practice. Therefore, the
execution time of the algorithm remains acceptable
although the subgraph matching algorithm is an NP-
complete problem.
5 PROTOTYPE SYSTEM
We will now describe the workflow of our
implemented prototype system. We will discuss
where and how the user needs to intervene in the
process, and how the automatic steps (classification,
segmentation and annotation) work.
5.1 User Interaction
User interaction serves two tasks: specify global
semantics and local semantics of a few models
interactively. For specifying global semantics, we
need to specify the number of clusters and choose
the training models for SVM classification. Once all
3D models have been classified, we choose a few
template models from each class and specify their
local semantics, including interactive segmentation
and annotation.
We use a semantic library (Tutenel et al., 2009)
to annotate models and model parts. The aim of the
semantic library is to provide a set of semantic
classes for each 3D model. A semantic class
describes detailed information about 3D models
associated to that class, ranging from class names
and physical properties, to relationships with other
classes (and therefore their associated models). For
example, in Fig. 6, the class “Table” consists of five
parts (4 instances of the “Table leg” class and 1 of
the “Table top” class) and inherits from the parent
class “Furniture”.
Figure 6: Specification of semantics of 3D models.
tabletop
table leg
table leg
table leg
table leg
tabletop
table leg
table leg
table leg
table leg
sub
-
AAG
AAG
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
102

5.2 Automatic Classification
We use SVM for classification due to its robustness
and simplicity. The RBF kernel function is usually
the first choice for SVM. This kernel function can
handle nonlinear problems by increasing the
dimensionality of space. However, in this work, we
use a linear kernel instead of RBF because the
dimensionality of the shape descriptor is large
(1024) (Hsu et al., 2003). In the example of Fig. 7,
the model with the red box is the training model,
which is accomplished as described in Section 5.1.
The rest of the models in Fig.7 are considered to be
similar to the training model by SVM. The
classification results are almost consistent with
human perception, except the last model, the
“Table” model, which is wrongly classified into the
group.
Figure 7: Automatic classification using training data.
Figure 8: The classification result after one iteration.
Only a part of similar models are classified into a
group by SVM with the limited training models
because we expect to reduce user interaction. Some
models, which belong to different classes, also end
up in the same group due to the semantic gap. The
relevance feedback can be used to improve the
classification result. The specified models in the end
are used as reference models to refine the
classification hyperplane of SVM. For example, in
Fig. 7, the models in the green box are specified
models. Fig. 8 shows the classification results after
using the new training models. The results improved
quite a lot compared with Fig. 7.
5.3 Automatic Segmentation
Once all the tagged models have been classified, we
rely on template models segmented interactively in
Section 5.1 to partition the other tagged models
automatically. For each class of tagged models, we
use the same segmentation method (and parameters)
of template models for segmentation. For example,
in Fig. 9 (a), the template model is segmented by
region growing (Pavlidis and Liow, 1990) and the
rest of the models as well. In Fig. 9 (b), the template
model is segmented by SDF (Shapira et al., 2008).
We need to further consider the value of parameters
of the SDF method. We use the average value of
parameters in the experiments if there are multiple
template models in the class. However, the SDF
method with the same parameters cannot guarantee
consistent segmentation even when the tagged
model is quite similar to the template model.
Figure 9: Automatic model segmentation based on
template models.
5.4 Automatic Annotation
The partitioned models are represented by an AAG,
and subgraph matching is used for automatic
annotation. Before subgraph matching, the nodes of
each AAG need to be sorted according to the
volume. It is appropriate to assume that nodes with a
large volume are more meaningful than the ones
with a small volume. Therefore, we will first search
the nodes with large volume in the procedure of
subgraph matching, which reduces the time
complexity and ambiguity if there are multiple
mappings between a sub-AAG and an AAG.
6 RESULTS
We used 3D models from the PSB (Shilane et al.,
template
template
(a)
(b)
A METHOD FOR SPECIFYING SEMANTICS OF LARGE SETS OF 3D MODELS
103

Table 1: Results of automatic specifying semantics of 3D models.
Class
name
3D
models
(m)
Classified models
(c)
Specified models
(n)
Global specification
rate (%)
Local specification
rate (%)
Average
specification rate (%)
1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
seat
furniture
77 26 37 38 22 31 32 33.8 48.1 49.4 84.6 83.8 84.2 28.6 40.3 41.6
table
furniture
78 24 43 47 21 37 41 30.8 55.1 60.3 87.5 86.0 87.2 26.9 47.4 52.6
car
vehicle
113 54 75 80 52 72 77 47.8 66.4 70.8 96.3 96.0 96.3 46.0 63.7 68.1
human
biped
149 115 130 134 76 85 87 77.2 87.2 89.9 66.1 65.4 65.7 51.0 57.1 59.1
winged
vehicle
242 139 171 171 101 124 124 57.4 70.7 70.7 72.7 72.5 72.5 41.7 51.2 51.2
Average
49.4 65.5 68.2 81.4 80.7 81.2 38.9 51.9 54.5
2004) to validate the framework proposed in this
paper. The database of PSB is classified with 4
resolutions, ranging from coarse level to detailed
level. The more detailed the level is, the more
categories, and the fewer models are contained in
each category. Since our framework is aimed at
specifying semantics of large sets of models, we
prefer to have sufficient models in each class.
Therefore, we chose “coarse1” level (1814 models
are divided into 38 categories) in our experiments.
We used global specification rate
, local
specification rate
and average specification
rate
as indicators for the performance of our
prototype system. These indicators are defined as
follows:
=
,
=
,
=
×
=
where m is the number of models in a given category
in PSB, c is the number of models automatically
classified by SVM, and n is the number of
automatically specified models. The global
specification rate indicates the automatically
classified models in the database, the local
specification rate indicates the automatically
specified models which are relative to classified
models, and the average specification rate indicates
the automatically specified models which are
relative to models in the database.
We set the number of categories to be 38 for
clustering and chose 4 tagged models of each
category as training models for SVM classification.
Once all the models of the PSB were classified, we
segmented and annotated 3 models of each class
interactively, and used these specified models as
template models for automatic segmentation and
annotation. Table 1 illustrates the results of 5 major
categories in the PSB with three iterations. Once the
Figure 10: Average specification rate with increasing
number of template models and iterations.
3D models have been classified by SVM, more than
80% (local specification rate) of the models can be
segmented and annotated automatically. However,
the SVM classifier cannot find all the 3D models
with the limited training models, because a class of
PSB usually contains several subclasses. Therefore,
the final average specification rate is only nearly
55%. An impression of the impact of relevance
feedback and template models is shown in Fig. 10.
The average specification rate can be improved,
although only to a limited extent, by increasing the
number of template models and iterations. We
usually need at least 2 template models of each
group and 2 iterations to get a good performance of
automatic annotation of models.
7 CONCLUSIONS
This paper presents a method for specifying
semantics of 3D models with limited interaction. All
the models in the database are first classified. For
each class, we segment and annotate a few template
models interactively. The rest of the models can be
separated based on segmentation methods (and
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
104

parameters) of template models. Automatic
annotation can be achieved by subgraph matching
which finds a map between a sub-AAG representing
the parts of the template model and an AAG
representing the parts of partitioned models. In the
end, the specified models are used to improve the
classification.
Our method can achieve a good rate of automatic
annotation of 3D models with limited user
interaction, especially for the 3D models that can be
separated into consistent parts. Man-made models
compared with freeform ones are easier to be
segmented into consistent parts because the
segmentation method has no parameters. Thus, man-
made models have a higher specification rate, which
is indicated by the average specification rate in Fig.
10.
Figure 11: Inconsistent segmentation results using the
same segmentation method.
However, in experiments, although we use the
same segmentation method (and parameters) to
segment similar models, sometimes we still get
inconsistent segmentation results which means the
model parts cannot be annotated successfully. In this
case, we can provide more template models of each
class for automatic segmentation and annotation. For
example, in Fig. 11, the two models from the class
“winged vehicle” are partitioned inconsistently (one
of the wings is segmented into two parts) with the
same segmentation algorithm. We cannot use the
template model (a) to annotate model (b). Therefore,
we also use model (b) as a template model for
automatic annotation of the class “winged vehicle”.
In future work, we will test more segmentation
methods, especially for freeform models. We will
also consider more geometric and topologic
relationships among segments in the procedure of
subgraph matching for automatic annotation.
ACKNOWLEDGEMENTS
The work of Xin Zhang has been supported by
Netherlands Organization for International
Cooperation in Higher Education (Nuffic). This
research has also been partly supported by the
GATE project, funded by the Netherlands
Organization for Scientific Research (NWO).
REFERENCES
Attene M., Falcidieno B., Spagnuolo M. (2006).
‘Hierarchical mesh segmentation based on fitting
primitives’, The Visual Computer, vol. 22(3), pp. 181
– 193.
Attene M., Robbiano F., Spagnuolo M., Falcidieno B.
(2009). ‘Characterization of 3D shape parts for
semantic annotation’, Computer-Aided Design, vol.
41(10), pp. 756 – 763.
Biasotti S., Giorgi D., Spagnuolo M., Falcidieno B.
(2008). ‘Reeb graphs for shape analysis and
application’, Theorerical Computer Science, vol.
392(1-3), pp. 5 – 22.
Bronsvoort W. F., Bidarra R., van der Meiden H. A.,
Tutenel T. (2010). ‘The increasing role of semantics in
object modeling’, Computer-Aided Design and
Applications, vol. 7(3), pp. 431 – 440.
Carpenter W. C. and Hoffman M. E. (1997). ‘Selecting the
architecture of a class of back-propagation neural
network used as approximators’, Artificial Intelligence
for Engineering Design, vol. 11, pp. 33 – 44.
Chen X., Golovinskiy A., Funkhouser T. (2009). ‘A
benchmark for 3D mesh segmentation’, TOG:
Proceedings of ACM SIGGRAPH, vol. 28(3), a.73.
Cordella L. P., Forggia P., Sansone C., Vento M. (2001).
‘An improved algorithm for matching large graphs’,
Proceedings of the 3rd International Association for
Pattern Recognition Workshop on Graph-Based
Representation in Pattern Recognition, Ischia, Italy,
pp. 149 – 159.
Giacinto G. and Roli F. (2004). ‘Bayesian relevance
feedback for content-based image retrieval’, Pattern
Recognition, vol. 37(7), pp. 1499 – 1508.
Golovinskiy A. and Funkhouser T. (2008). ‘Randomized
cuts for 3D mesh analysis’, Proceedings of ACM
SIGGRAPH Asia, vol. 27(8), a.145.
Golovingskiy A. and Funkhouser T. (2009). ‘Consistent
segmentation of 3D models’, Computers & Graphics,
vol. 33(3), pp. 262 – 269.
Han E. H. and Karypis G. (2000). ‘Centroid-based
document classification: analysis and experimental
results’, Proceeding of 4th European Conference on
Principles of Data Mining and Knowledge Discovery,
Lyon, France, pp. 424 – 431.
Hsu C. W., Chang C. C., Lin C. J. (2003). ‘A practical
guide to support vector classification’, Technical
report, Department of Computer Science, National
Taiwan University.
Kalogerakis E., Hertzmann A., Singh K. (2010). ‘Learning
3D mesh segmentation and labeling’, TOG:
Proceedings of ACM SIGGRAPH, vol. 29(4), pp.
a.102.
(a)
(b)
A METHOD FOR SPECIFYING SEMANTICS OF LARGE SETS OF 3D MODELS
105

Kessing J., Tutenel T., Bidarra R. (2009). ‘Services in
game worlds: a semantic approach to improve object
interaction’, Proceedings of the International
Conference on Entertainment Computing, ICEC 2009,
Paris, France, pp. 276 – 281.
Lai Y. K., Hu S. M., Martin R. R., Rosin P. L. (2008).
‘Fast mesh segmentation using random walks’,
Proceedings of the ACM symposium on Solid and
Physical Modeling, New York, U.S.A., pp. 183 – 191.
Novotni M. and Klein R. (2004). ‘Shape retrieval using
3D Zernike descriptors’, Computer-Aided Design, vol.
36(11), pp. 1047 – 1062.
Novotni M., Park G. J., Wessel R., Klein R. (2005).
‘Evaluation of kernel based methods for relevance
feedback in shape retrieval’, Proceeding of the 4th
International Workshop on Content-Based Multimedia
indexing (CBMI), Riga, Latvia.
Osada R., Funkhouser T., Chazelle B., Dobkin D. (2002).
‘Shape distributions’, ACM Transactions on Graphics,
vol. 21(4), pp. 807 – 832.
Pavlidis T. and Liow Y. T. (1990). ‘Integrating region
growing and edge detection’, IEEE Transactions on
Pattern Analysis and Machine Intelligence, vol. 12(3),
pp. 225 – 233.
Robbiano F., Attene M., Spagnuolo M. (2007). ‘Part-
based annotation of virtual 3D shapes’, Proceedings of
the International Conference on Cyberworlds,
Washington D.C., U.S.A., pp. 427 – 436.
Rocchio J. J. (1971). ‘Relevance feedback in information
retrieval’, the SMART Retrieval System: Experiments
in Automatic Document Processing, pp. 313 – 323.
Saupe D. and Vranic D. V. (2001). ‘3D model retrieval
with spherical harmonics and moments’, Proceedings
of the 23
rd
DAGM-Symposium, Munich, Germany, pp.
392 – 397.
Schmidt D. C. and Druffel L. E. (1976). ‘A fast
backtracking algorithm to test directed graphs for
isomorphism using distance matrices’, Journal of
ACM, vol. 23(3), pp. 433 – 445.
Schnitman Y., Caspi Y., Cohen-Or D., Lischinski D.
(2006). ‘Inducing semantic segmentation from an
example’, Proceedings of Computer Vision – ACCV,
Hyderabad, India, pp. 374 – 384.
Shapira L., Shamir A., Cohen-Or D. (2008). ‘Consistent
mesh partitioning and skeletonisation using the shape
diameter function’, The Visual Computer, vol. 24(4),
pp. 249 – 259.
Shilane P., Min P., Kazhdan M., Funkhouser T. (2004).
‘The Princeton shape benchmark’, Proceedings of
Shape Modeling International (SMI), Genova, Italy,
pp. 167 – 178.
Smeulders A. W. M., Worring M., Santini S., Gupta A.,
Jain R. (2000). ‘Content-based image retrieval at the
end of the early years’, IEEE Transactions on Pattern
Analysis and Machine Intelligence, vol. 22(12), pp.
1349 – 1380.
Tangelder J. W. H. and Veltkamp R. C. (2004). ‘A survey
of content based 3D shape retrieval methods’,
Proceedings of International Conference on Shape
Modeling and Applications, Palazzo Ducale, Genova,
Italy, pp. 145 – 156.
Tu Z., Chen X., Yuille A. L., Zhu S. (2005). ‘Image
parsing: unifying segmentation, detection and
recognition’, International Journal of Computer
Vision, vol. 63(2), pp. 113 – 140.
Tutenel T., Bidarra R., Smelik R. M., de Kraker K. J.
(2008). ‘The role of semantics in games and
simulation’, ACM Computer in Entertainment, vol.
6(4), pp. 1 – 35.
Tutenel T., Bidarra R., Smelik R. M., de Kraker K. J.
(2009). ‘Rule-based layout solving and its application
to procedural interior generation’, Proceedings of the
CASA’09 Workshop on 3D Advanced Media in
Gaming and Simulation, Amsterdam, the Netherlands,
pp. 15 – 24.
Ullmann J. R. (1976). ‘An algorithm for subgraph
isomorphism’, Journal of ACM, vol. 23(1), pp. 31 –
42.
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
106
