KNOWLEDGE-DRIVEN HARMONIZATION MODEL

FOR TONAL MUSIC

Mariusz Rybnik

and Władysław Homenda

1,2

Faculty of Mathematics and Computer Science, University of Bialystok, ul. Sosnowa 64, 15-887, Bialystok, Poland

Faculty of Mathematics and Information Science, Warsaw University of Technology

Pl. Politechniki 1, 00-661, Warsaw, Poland

Keywords:

Musical work, Harmony, Harmonization, Tonality, Knowledge-based systems.

Abstract:

The paper proposes an approach to an automatic harmonization of musical work, and is based on the knowl-

edge of music theory. It may be described as knowledge-based, being in contrast to a data-driven approach,

that extracts relationships from examples. Our approach emphasizes universality, understood as the possibility

of direct model modiﬁcations in order to obtain varied harmony characteristics (as for example a complicated

and unusual harmony, or a simple harmony using only a small subset of harmonic functions and few modi-

ﬁers). Therefore it is conﬁgurable by changing the internal parameters of harmonization mechanisms (among

others: harmonic functions excitements with note pitches, note importance regarding among others horizontal

position in measure and vertical position in voices structure, successions of neighboring harmonic functions),

as well as importance weights attached to each of these mechanisms.

1 INTRODUCTION

Harmony is an important element of tonal music, it

deﬁnes the vertical relation between notes, as by def-

inition opposed to melody - horizontal succession of

notes in speciﬁc voice (Sikorski, 2003). In fact, how-

ever, the harmonic relations of the leading melody (re-

garding mono- or homophony) are largely depending

on the horizontal succession of notes and intervals be-

tween them. In a melody one can frequently detect

harmonic passages that follow harmonic chords (with

smaller or larger deviations). Similar, but obviously

much stronger harmonic relations are to be found in

accompaniment, where the melody is less (or even

not at all) important, as the main goal is to deﬁne the

background for the leading melody. The obvious ex-

ception to these assumptions are polyphonic musical

works. They tend to cultivate two or more indepen-

dent voices, that compete for attention but also have

to cooperate harmonically, usually indicating strong

harmonic relations.

Automatic harmonization can be seen as a prob-

lem belonging to the area of computer music com-

posing. Over the years many various approaches

and techniques were used to solve this or simi-

lar problems, just to mention a few: Expert Sys-

tems (Cope, 1987)(Ebcioglu, 1993), Neural Net-

works (Hild, 1992), Constraints and probabilistic ap-

proaches (Pachet and Roy, 2001) (Pachet, 1995), evo-

lutionary algorithms (Prisco and Zaccagnino, 2009).

The common limitation for such approaches seems

to be the lack of universality (production of slightly

unpredictable results) and (for some techniques) need

for large learning database or extensiveamount of cal-

culations. Our approach is based on the use of theo-

retical music knowledge and is aimed at solving these

disadvantages.

The paper is organized as follows: Section 2

presents basic concept of harmony in tonal music,

Section 3 describes in detail the proposed harmoniza-

tion model and explains used mechanisms, Section

4 introduces a short example of experimental results.

Section 5 concludes the paper, discuses conﬁguration

and universality properties and suggests future works.

2 HARMONY IN TONAL MUSIC

The process of creating accompaniment to a lone

melody (known as homophony) can be divided into

two phases. The ﬁrst is harmonization (creation of

harmonic functions and corresponding chords), and

the second phase is creation of accompaniment with

the use of previously obtained harmony.

445

Rybnik M. and Homenda W..

KNOWLEDGE-DRIVEN HARMONIZATION MODEL FOR TONAL MUSIC.

DOI: 10.5220/0003889604450450

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 445-450

ISBN: 978-989-8425-95-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Harmonic functions related to scale degrees.

Degree

Function

Name Symbol

Shift

minor major

1 Tonic T 0 0

2 Subdominant 2nd S

2 2

3 Tonic 3rd T

4 3

4 Subdominant S 5 5

5 Dominant D 7 7

6 Tonic 6th T

9 8

It is important to stress that in most cases there

is no single, ultimate harmony solution for a given

melody, usually there are many possibilities, rang-

ing from the simplest and obvious to the compli-

cated and non-trivial ones. The choice depends on

the style of music, as well as the capabilities of in-

strument/orchestration and the abilities of perform-

ers/harmonizers. There are also cases, when no addi-

tional information, except for the leading melody and

harmonic functions, is needed to perform the music.

Common example is improvised

a vista accompani-

ment to songs, when playing the guitar or piano.

For the purposes of this paper we have focused on

a tonal system with two basic scales: major and mi-

nor (natural minor as well as harmonic and melodic

modiﬁcations). Our considerations and experiments

are based on six harmonic functions (built on 1

, 2

, 4

, 5

and 6

grade of major/minor scales) with

basic modiﬁcations: adding seventh (minor and ma-

jor), ninth (minor and major), sixth (minor and ma-

jor). We have omitted incomplete Dominant seventh

built on grade 7

as being equivalent to Dominant

seventh with omitted root, alterations and higher in-

tervals (alike eleventh, thirteenth), that may be seen as

dissonances that are meant to resolve (and enrich har-

mony), rather than integral harmonic modiﬁers. The

tonal harmonic functions along with names and sym-

bols are presented in Table 1.

3 PROPOSED HARMONIZATION

MODEL

The proposed harmonization model is based on sev-

eral mechanisms, that are supposed to closely follow

music theory:

1. Particular notes have various harmonic impor-

tance,

2. Each note may excite (ﬁt to) one or several har-

monic functions based on its pitch and consid-

ered function components,

3. Some harmonic functions are more likely to oc-

cur than others (the most popular example being

Tonic - a base and consolation for vast majority of

tonal music), therefore it is preferable to prioritize

functions being more frequently used,

4. Speciﬁc harmonic functions’ successions are

more or less probable, therefore it is possible

to support more likeable (frequent) successions

(alike Dominant → Tonic or Tonic → Subdomi-

nant).

The mechanisms are implemented in possibly in-

dependent way and weighted (using a range [0;1]) in

order to easily conﬁgure the degree of inﬂuence (or

eliminate the inﬂuence at all) on the ﬁnal harmoniza-

tion, in comparison with the other mechanisms.

3.1 Data Representation of Harmonic

Functions

Each harmonic function is stored in a structure that

contains a vector (of length 6, as we consider 6

different diatonic functions) of Harmonic Function

Strengths and a corresponding vector of modiﬁers.

In our experiments the modiﬁers are mostly limited

to sevenths, with occasional ninths and in rare cases

to sixths (sixth is present in so-called Chopin chord:

Dominant with seventh and natural or augmented

sixth instead of ﬁfth, resolving down to ﬁrst degree of

scale). The diatonic function with modiﬁers is equiv-

alent to chords i.e. Tonic with modiﬁer seventh in key

G-major is equivalent to G

. Some modiﬁers cover

others, i.e. a chord with ninth is supposed to gorge a

chord with seventh.

Musical piece is decomposed into elementary har-

monic fragments (deﬁned as indivisible musical piece

unit with one diatonic function attached to). For ex-

perimental evaluation we have chosen fragments of

ﬁxed lengths at the most two beats or less depend-

ing on the time of musical work, i.e. for the time

it would be two beats for the ﬁrst harmonic frag-

ment of measure and one beat for the remaining frag-

ment of measure; for the time

one harmonic frag-

ment per measure would most probably be sufﬁcient.

Each harmonic unit is processed independently - with

exception of supporting speciﬁc successions of har-

monic functions (see Section 3.6) - therefore it does

not require additional modiﬁcations, as shorter har-

monic fragments will also naturally have lower inﬂu-

ence on larger neighbors. In most cases this simplis-

tic division would be sufﬁcient, as harmonic functions

rarely change in practice more frequently, while over-

fragmentation could result in lower accuracy of har-

monization.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

446

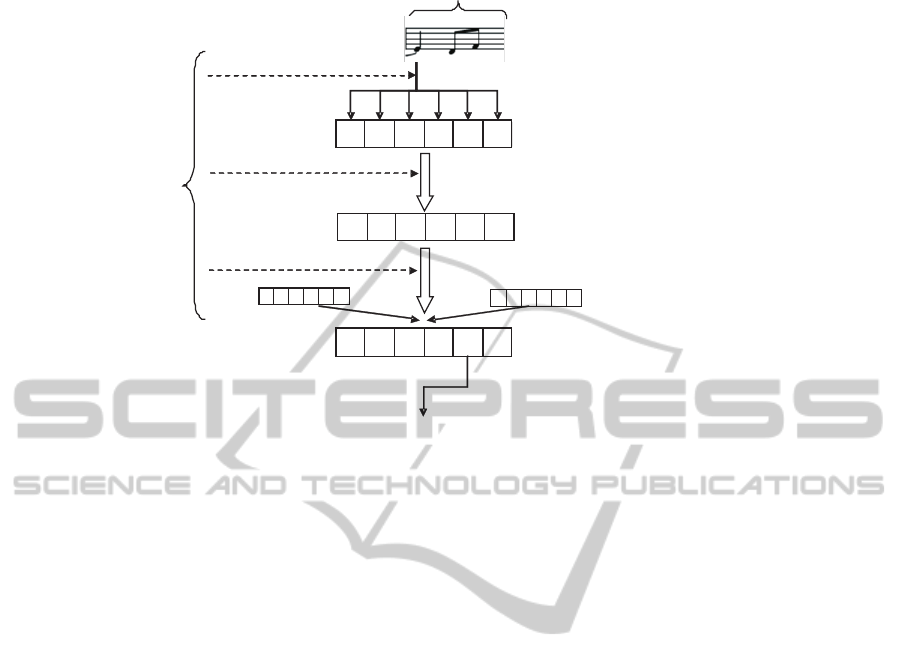
2. Excitation

3. Function Popularity

4. Function Succession

5. Decision

Dominant seventh (G

major)

Mechanisms' configuration weights <0,1>

Harmonic Fragment

…

Predecessor Successor

0.43 1.33 0.68 0.70 1.14 0.39

0,43 0,80 0,48 0,63 1,08 0,25

0,70 1,22 0,73 1,04 1,90 0,42

0,8 1 0,42 0,83 0,00 0,87 0,51

0,81 0,42 0,83 0,00 0,87 0,51

1. Determination

of Note Importance

Note Importance global weight

Function Popularity global weight

Function Succession global weight

Figure 1: Harmonization model ﬂow.

3.2 The Flow of Proposed Model

The ﬂow of proposed model for an exemplary har-

monic fragment is presented in Figure 1, and proceeds

as follows:

1. The harmony of particular fragment is evaluated

by examining all notes from this fragment. Each

note is attached with Note Importance weight ac-

cording to the exemplary set of rules from Section

3.3.

2. Each note excite (add a value to Function

Strengths vector) one or - in most cases - few cor-

responding diatonic functions by being a speciﬁc

chord component, with degree deﬁned by a Func-

tion Excitation Matrix (Section 3.4).

3. When all the notes are evaluated the vector of a

Function Strengths is element-wise multiplied by

a Function Popularity Vector (Section 3.5), what

primarily acts as encouragement for more popular

functions. It may also be used to serve a different

purpose, if one wishes for a rich and uncommon

harmony).

4. After all harmonic fragments are evaluated, the

mechanism for supporting particular function suc-

cessions is applied. The degrees of desire for a

speciﬁc succession of harmonic functions are de-

ﬁned in a Function Succession Matrix (Section

3.6). They serve as an additional modiﬁers for

vectors of the Function Strengths with regards

to direct predecessor and successor. The modi-

ﬁcation occurs twice for every fragment (except

for the marginal fragments), the ﬁrst time as a

predecessor, and the second time as a successor.

The modiﬁcations are calculated for each func-

tion succession possible (a total of 36 combina-

tions possible for 6 recognized functions, modi-

ﬁers not taken into account) and are multiplied by

both corresponding function strengths and addi-

tionally by a 1/12 factor in order to keep them in

the original Function Strengths range.

5. After applying the succession modiﬁcations a de-

cision (of type winner-takes-all) is made for each

Harmonic Fragment, based on values of the Func-

tion Strengths. The winning diatonic function is

translated into chord, depending on the key and

attached with chord modiﬁers (i.e. seventh, ninth)

stored during Excitation.

Each omitable mechanism (Note Importance,

Function Popularity, Function Succession) is attached

with an overall Global Conﬁguration Weight from the

range [0;1] (as seen in Figure 1), that may be used

to ﬁne tune or disable the inﬂuence of these mech-

anisms on the ﬁnal harmonization result. Excitation

is the essential mechanism to obtain the Function

Strengths, therefore it is not weighted in similar man-

ner. The mechanisms are based on matrices (Exci-

tation, Function Succession), vectors (Function Pop-

ularity) or rules (Note Importance) that offer many

substantial and direct conﬁguration possibilities.

KNOWLEDGE-DRIVEN HARMONIZATION MODEL FOR TONAL MUSIC

447

Table 2: Determining note importance.

Condition Importance

Note at the end of a tie 0.4

Note on the 1

beat 1.0

Note on the 3

beat 0.9

Other notes 0.6

3.3 Notes Importance Determination

For determining notes importance we have consid-

ered:

• the position in measure - notes on-beat (at inher-

ently accented parts of measure) are very impor-

tant (especially 1

beat and a little less 3

beat for

time

), while off-beat (at generally unaccentu-

ated parts of measure, as for example 2

and 4

for time

) are less signiﬁcant. Notes occur-

ring in-between these main beats are harmonically

least important.

• the notes that are at the end of ties have

minor contribution to the harmony, because

when played on string instruments (among others:

grand piano, upright piano, guitar) they are not hit

again,

• the long notes are usually more important than

the short ones,

• the notes that are easily-heard by human ear

are placed in extremal voices (highest and low-

est notes), the notes in the middle voices are

harder to hear and therefore contribute less to the

harmony of musical work,

• accentuation increases the volume and the har-

monic value of the note.

For the experimental evaluation we have deter-

mined a set of the note importance rules as described

in Table 2. As we deal only with a single melody we

neglected the voice position (not relevant in this case)

and length of notes (do not contribute a lot in this

case), which would be however important for music

works with many melodic parts.

3.4 Implementation of Tonal Functions

Excitation by Notes

In order to deﬁne diatonic functions we had to detect

the key of musical work, that may be obtained in sim-

pliﬁed but effective method, by analyzing the pitch of

the last note in the leading voice and the key signature.

This is possible due to the fact that in vast majority of

cases melody ends on 1

degree of tonic scale, being

the resolution of tension. There are only marginal ex-

ceptions to this scheme (disregarding modulations).

In order to deﬁne the excitation of diatonic func-

tions by the notes occurring in the melody or the ac-

companiment we have deﬁned a table of excitation

(Table 3), where each diatonic function may be ex-

cited by particular note with a speciﬁed degree. This

is relative to the pitch of the note in question, as well

as the pitches of the notes occurring in the tonal func-

tions themselves. We have deﬁned the degree of exci-

tation in the range of [0,1], assigning:

• greater degrees [0.8;1.0] to the most typical chord

components as root note, third and ﬁfth,

• moderate degrees [0.4;0.6] to less speciﬁc compo-

nents: sixth, seventh, ninth with ,occasional modi-

ﬁcation of natural third, that serves making major

chords from naturally minor chords, what serves

mostly as tonicization (local Dominant → Tonic

resolution)

• small degrees [0.1;0.2] to rare modiﬁcations of

natural sixth and seventh, ninth.

A similar table has been prepared for minor scales,

the obvious differences are the natural qualities of

diatonic functions, the less obvious would be frequent

conversion from naturally minor Subdominant and

Dominant to major ones (occurring commonly in

melodic variation of scale and partially in harmonic

variation).

3.5 Function Popularity

The goal of determining function popularity is to di-

rectly prioritize frequently occurring tonal functions

(like Tonic, Subdominant, Dominant) and in this way

enforce them to occur more frequently than less pop-

ular derivative ones. The goal is indirectly obtainable

by using lower coefﬁcients in the Functions Succes-

sion Matrix (described in Section 3.6), but it is ob-

viously easier to control directly. For experimental

studies we have used the Function Popularity Vector

as speciﬁed in Table 4.

3.6 Succession of Harmonic Functions

The succession of harmonic functions (horizontal re-

lations between neighboring harmonic functions) is

implemented using encouragement of more probable

combinations, with moderation of less likable ones.

This is done using a matrix of Functions Succession.

The exemplary matrix for major scale is presented in

ICAART 2012 - International Conference on Agents and Artificial Intelligence

448

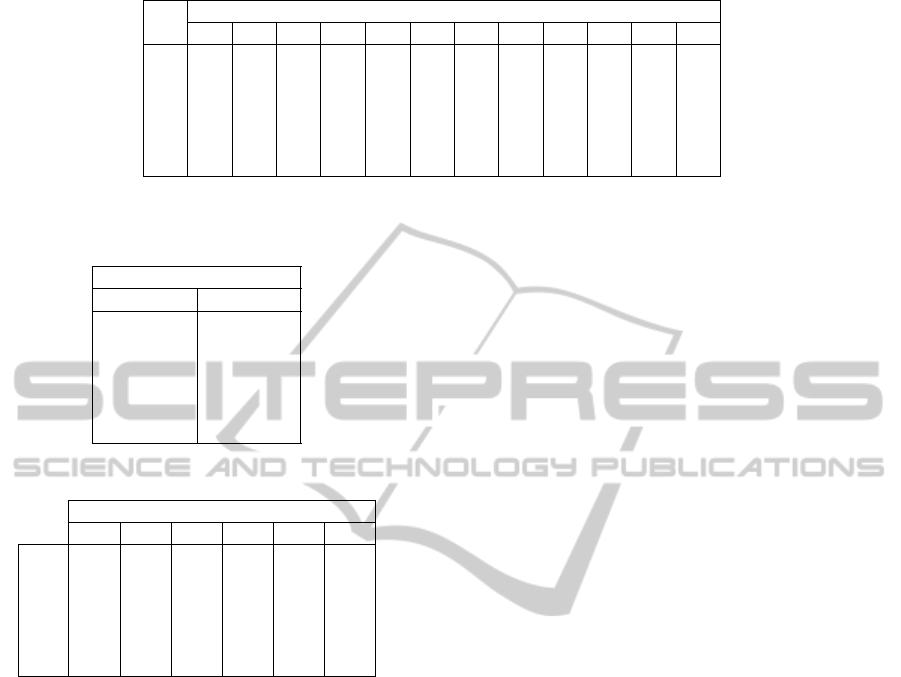
Table 3: Table of excitation for major scales.

Absolute shift from function root note[in semitones]

0 1 2 3 4 5 6 7 8 9 10 11

1.0 0.0 0.0 0.9 0.1 0.1 0.0 0.8 0.0 0.0 0.4 0.0

D 1.0 0.5 0.2 0.1 0.9 0.1 0.0 0.8 0.0 0.4 0.6 0.1

S 1.0 0.0 0.0 0.1 0.9 0.1 0.0 0.8 0.0 0.0 0.4 0.0

1.0 0.0 0.0 0.9 0.1 0.1 0.0 0.8 0.0 0.0 0.4 0.0

T 1.0 0.0 0.0 0.1 0.9 0.1 0.0 0.8 0.0 0.0 0.4 0.0

Table 4: Function popularity.

Tonal function

Name Popularity

T 1.0

0.6

0.7

S 0.9

D 0.95

0.65

Table 5: Functions Succession Weights for major scales.

Transfer into:

T S

S D T

0,4 0,8 0,3 0,8 0,7 1,0

D 0,9 0,4 0,7 0,3 1,0 0,8

S 0,7 0,4 0,4 1,0 0,9 0,5

0,3 0,2 1,0 0,5 0,6 0,8

0,2 1,0 0,2 0,5 0,9 0,4

T 1,0 0,4 0,3 0,8 0,9 0,6

Table 5. The matrix for minor scale is very similar

and therefore not presented here.

The values in the matrix were determined in or-

der to prioritize most likable successions, like ca-

dence, but also allowing more complicated succes-

sions It is worth mentioning that the most supported

quasi-succession is maintaining the current function

(no change) with maximum degree of support: 1.0.

That allows more efﬁcient handling of the common

case where harmonic functions change less frequently

than hard-coded (in our experiments) two beats. It is

also important to mention that the support of succes-

sion occurs only between harmonically determinable

half-measures, excluding these that do not contain

notes at all (only pauses) or contain only ongoing

tied notes from previous beats. It is assumed that

such fragments continue the previous harmonic func-

tion (which is a slight oversimpliﬁcation as it does not

have to be always true). The succession support oc-

curs forwards and backwards with a degree deﬁned

by the sum of products of the neighboring Function

Strengths and a succession weight from the Functions

Succession matrix for each possible succession.

4 EXPERIMENTAL RESULTS

This section presents the exemplary results of ho-

mophony harmonizations using proposed approach.

We have implemented and applied the model to mu-

sical works containing a single melody (monophony)

with no key changes, as we considered it more of a

challenge (more harmonic uncertainty) rather than us-

ing musical works with accompaniment, where har-

monic functions are generally much easier to detect

(depending on the degree of complication and the pur-

pose of musical work). It is however important to

stress that the proposed harmonization model remains

viable for almost every musical piece, regardless of

number of voices, as long as it is maintained in tonal

system i.e. uses either major or minor scale (possi-

bly with slight modiﬁcations). Use of higher number

of voices (chords) would ideally require a customized

Notes Importance determination (as described in Sec-

tion 3.3), in order to detect and prioritize more im-

portant voices and attenuate the less important ones.

Efﬁcient harmonization of musical works with key

changes (known as modulations)would require detec-

tion of such changes and adequate updating of tonal

base and/or minor/major properties.

The results in Figure 2 present two different har-

monies for a short homophony fragment. The func-

tions and chords at the top were obtained for global

conﬁguration weights (respectively: Notes impor-

tance, Function popularity, Functions Succession)

equal to [0.4,0.4,0.4], while at the bottom with global

parameters [0,0,0.8]. In the ﬁrst case the less popular

functions are moderated, while in the second one the

less popular functions are present and there is more

continuity in successions. A change of global weights

alone - without the modiﬁcation of the inner parame-

ters - gives different and interesting results.

KNOWLEDGE-DRIVEN HARMONIZATION MODEL FOR TONAL MUSIC

449

Figure 2: Two different harmonizations for a homophony fragment.

5 CONCLUSIONS AND FUTURE

WORKS

In this paper we have presented the harmonization

model based on the knowledge of music theory. The

main goal of this approach is achieving universality

and obtaining direct control over various harmoniza-

tion mechanisms. It is important to stress the conﬁg-

uration possibilities and universality of the proposed

model: as it is not data-driven but knowledge-driven,

it provides the ease of control of the behavior and, to

some extent, results of harmonization. As opposed

to the data-driven approaches (taught with examples)

our methodology does not need to be fed with large

or representative sample of data (requiring data gath-

ering, selection and often producing hard to control

results). It may be used in many variants relying only

on the theoretical knowledge. With modiﬁcations of

underlaying conﬁguration data one can try (and in

some cases be guaranteed) to achieve multiple valu-

able tasks, such as:

• deﬁning the Note Importance rules tuned to vari-

ous musical pieces;

• deﬁning the Function Excitation Matrix to eas-

ily generate very rare or very simple func-

tions/modiﬁcations;

• deﬁning the Function Popularity Vector to moder-

ate, forbid or encourage speciﬁc tonal functions;

• deﬁning the Function Succession Matrix to mod-

erate, forbid or encourage speciﬁc harmonic func-

tion successions;

• changing the Weights of Harmonization Mecha-

nisms in order to tune the model to the speciﬁc

needs and expectations;

• iterate through various conﬁgurations in order

to quickly generate various (possibly interesting)

harmonies for the same musical work.

Future works in the area will be conducted in the

following directions:

• development and evaluation of presented harmo-

nization model,

• developing criteria for evaluation of obtained har-

mony,

• automatic parametrization of the harmonization

model based on the above-mentioned evaluation,

• determination of conﬁguration matrices and pa-

rameters for the different styles of musical works,

like jazz, classical music, popular music, etc.

• accompaniment generation based on the harmony

provided by model,

• existing accompaniment modiﬁcation and enrich-

ment based on the independent harmony provided

by model.

REFERENCES

Cope, D. (1987). An expert system for computer-assisted

music composition. In Computer Music Journal, vol-

ume 11 (4), pages 30–46.

Ebcioglu, K. (1993). An expert system for harmonizing

four-part chorales. In Machine Models of Music,

pages 385–401. MIT Press.

Hild, H. Feulner, J. M. W. (1992). Harmonet: A neural net

for harmonizing chorals in the style of j.s. bach. In

Advances in Neural Information Processing 4.

Pachet, F. and Roy, P. (2001). Musical harmonization with

constraints: A survey. In Constraints Journal, volume

6(1), pages 7–19. Kluwer Publisher.

Pachet, F. Roy, P. (1995). Mixing constraints and objects:

a case study in automatic harmonization. In TOOLS

Europe ’95, pages 119–126. Prentice-Hall.

Prisco, R. D. and Zaccagnino, R. (2009). An evolutionary

music composer algorithm for bass harmonization. In

Applications of Evolutionary Computing. LNCS.

Sikorski, K. (2003). Harmony part 1 and 2 [in Polish].

Polskie Wydawnictwo Muzyczne.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

450