TVT: A SOFTWARE VERIFICATION PACKAGE FOR THE

INTERACTIVE LEARNING OF FORMAL PROGRAMMING

TECHNIQUES

An Educational Experience

Rafael del Vado V

ırseda, Fernando P

erez Morente and Eduardo Berbis Gonz

alez

Departamento de Sistemas Inform

aticos y Programaci

on, Universidad Complutense de Madrid, Madrid, Spain

Keywords:

Software Tools, Semantic Tableaux, Veriﬁcation, Debugging, Invariants.

Abstract:

While Computational Logic plays an important role in several areas of Computer Science (CS), most edu-

cational software developed for teaching logic is not suitable to be used directly in other portions of the CS

education domain where the application of logical notions is usually required. In this paper we describe the

logic teaching tool TVT based on semantic tableaux that has been developed to help the students to use logic as

a formal proof technique in other advanced topics of CS, such as the veriﬁcation of algorithms, the algorithmic

debugging of imperative programs, the formal design of invariants, and the design and derivation of algorithms

from logical speciﬁcations, which are at the basis of the formal learning of programming techniques and good

development of software. We present the design, implementation, and results of the evaluation of this tool by

means of several educational experiences during the academic courses 2009/2010 and 2010/2011. From the

results of these experiences we conclude that the use of the TVT tool in the current CS teaching can help our

students to understand more advanced CS concepts and to clarify the formal process involved in the design

and analysis of correct and efﬁcient imperative programs.

1 INTRODUCTION

Computational Logic is a subject that is taught in

the ﬁrst courses of almost all the Computer Scien-

ce (CS) universities around the world. The syllabus

of the course usually includes the syntax and seman-

tics of propositional and ﬁrst-order logic, as well as

some formal proof techniques such as natural deduc-

tion, resolution, or semantic tableaux (Fitting, 1990).

In some cases, there are some lectures devoted to

explain basic concepts on logic programming and

practical work using a Prolog interpreter. However,

while Computational Logic plays an important role

in several areas of CS, most of the educational soft-

ware developed for teaching logic ignores their pos-

sible application in a larger number of subjects of

the CS education domain. Many educational tools

in this area (e.g., logic inference assistants and proof

visualizers) have been developed with different de-

grees of success, and its utility has been proved by

means of several educational experiments and publi-

cations. An actual and extensive collection of them

can be found at http://www.ucalgary.ca/aslcle/logic-

courseware and (Huertas, 2011). Unfortunately, al-

though advanced logical notions are applied in su-

perior courses, this educational logic software is not

suitable for being used in these subjects.

The aim of this work is to describe an innovative

methodology based on the logic teaching tool TVT

that uses semantic tableaux to visualize formal proofs

on advanced topics in CS, such as the design of cor-

rect and efﬁcient algorithms from logical speciﬁca-

tions. A semantic tableau (Fitting, 1990) is a seman-

tic but systematic method of ﬁnding a model for a

given set of formulas Γ, usually classiﬁed as a refuta-

tion system because a theorem ϕ is proved from Γ by

getting its negation Γ  ¬ ϕ. Our major contribution is

the implementation of new tableau methods that pro-

vide semantically reach feedback to the students in or-

der to help them to understand the formal reasonings

performed in the process of verifying the correctness

of algorithms. Moreover, it allows to perform an algo-

rithmic debugging of programs following a classical

idea from Shapiro (Shapiro, 1983), that proposes to

replace computation traces by computation trees with

program fragments attached to their nodes in the de-

bugging process. As novelty in this work, we pro-

pose to use semantic tableaux as computation trees to

del Vado Vírseda R., Pérez Morente F. and Berbis González E..

TVT: A SOFTWARE VERIFICATION PACKAGE FOR THE INTERACTIVE LEARNING OF FORMAL PROGRAMMING TECHNIQUES - An Educational

Experience.

DOI: 10.5220/0003894400770082

In Proceedings of the 4th International Conference on Computer Supported Education (CSEDU-2012), pages 77-82

ISBN: 978-989-8565-07-5

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

show the students that they can reason on the results

of the execution of a program only considering the

meaning of the program itself and ignoring complex

operational details.

We have tested the TVT tool through the academic

courses 2009/ 2010 and 2010/2011, performing some

educational experiments to estimate the beneﬁts for

our students of using the tool as a complement to

scheduled regular classes. This evaluation has been

carried out by means of several tests, some of them

managed in an online platform with open access to

the students, and the other ones in a CS laboratory

with a controlled group. We show the results of these

educational experiments and the beneﬁts of using the

TVT tool in the teaching of advanced CS concepts

involving the formal veriﬁcation and the algorithmic

debugging of imperative programs. We believe that

these educational experiences prove that our imple-

mentation based on tableaux provides an excellent

training to the students in the practical application

of advanced logic concepts to perform different CS

tasks.

2 THE TVT TOOL

Solving logical exercises is usually done with pen

and paper, but educational tools can offer more use-

ful pedagogical possibilities. The role of this edu-

cational software is to facilitate the student’s grasp

of the target procedures of education, and to provide

teamwork and communication between teachers and

students (van ditmarsch, 2005).

Our Tableaux Veriﬁcation Tool,

named TVT (see the current version at

gpd.sip.ucm.es/CSEDU2012/TVT.zip), is an edu-

cational application based on ﬁrst-order semantic

tableaux with equality and uniﬁcation (Fitting, 1990)

used as a support for the teaching of deductive rea-

soning at an elementary university level for Computer

Science students. The tool helps our students to learn

how to build semantic tableaux, and to understand

the philosophy of this proof device using it not only

to establish consistency/inconsistency or to draw

conclusions from a given set of premises, but also for

veriﬁcation and debugging purposes as we propose

in this paper. Our ﬁrst year students have learnt

tableau calculus in the classroom and this software

has helped them to understand advanced CS concepts

visualizing and producing their own proof trees.

The tool consists of two main parts: one that pro-

duces ﬁrst-order tableaux, and another one based on

this tableaux methodology for veriﬁcation and debug-

ging of algorithms. In both cases, the application pos-

sesses a drawing window where trees will be graphi-

cally displayed. The major functional interface of the

TVT tool is shown in Figure 1. The user interacts with

the prover through this graphical interface. In the fol-

lowing sections we describe the use of the tool and

their main features by means of a running example.

3 FORMAL VERIFICATION

The main novelty of the TVT tool is to train our stu-

dents in the art and science of specifying correctness

properties of algorithms and proving them correct.

For this purpose, we use the classical approach de-

veloped by Edsger W. Dijkstra and others during the

1970s (Dijkstra, 1976). We use a guarded command

language to denote our algorithms A, represented by

functions fun A ffun that may contain variables (x, y,

z, etc.), value expressions (e) and boolean expressions

(B). The code of an algorithm is built out of the skip

(skip) and assignment statements (x := e) using se-

quential composition (S

), conditional branching

(if B then S

else S

fif), and while-loops (while

B do S fwhile). This language is quite modest but

rich enough to represent sequential algorithms in a

succinct and elegant way. As an illustrative example,

we consider a simple algorithm divide to compute the

positive integer (int) division between a and b with

quotient c and remainder r (represented in TVT on

the left and bottom of Figure 1):

fun divide (a, b : int ) dev < c, r : int >

c := 0 ; r := a ;

while r ≥ b do

c := c + 1; r := r − b

fwhile

ffun

It becomes obvious that neither tracing nor testing

can guarantee the absence of errors in algorithms.

To be sure of the correctness of an algorithm one

has to prove that it meets its speciﬁcation (Dijkstra,

1976). A speciﬁcation of an algorithm A consists

of the deﬁnition of a state space (a set of program

variables), a precondition P and a postcondition Q

(both predicates expressing properties of the values

of variables), denoted as {P} A {Q}. Such a triple

means that Q holds in any state reached by executing

A from an initial state in which P holds. For exam-

ple, a formal speciﬁcation for the divide function

(represented in TVT on the left and top of Figure 1) is:

{P : a ≥ 0 ∧ b > 0 }

fun divide (a, b : int ) dev < c, r : int >

{Q : a = b ∗ c + r ∧ r ≥ 0 ∧ r < b }

CSEDU2012-4thInternationalConferenceonComputerSupportedEducation

Figure 1: The TVT tool for the formal learning of programmming techniques.

An algorithm together with its speciﬁcation is viewed

as a theorem. The theorem expresses that the program

satisﬁes the speciﬁcation. Hence, all algorithms re-

quire proofs (as theorems do). Following (Kaldewaij,

1990), the veriﬁcation is based on a loop invariant I

supplied by the designer or by some invariant-ﬁnding

tool (in our example a = b ∗ c + r ∧ r ≥ 0 ∧ b > 0), a

bound function C for termination (in our example r),

and the following ﬁve proofs (see again Figure 1):

• {P} c := 0 ; r := a {I}.

• {I ∧ r ≥ b} c := c + 1; r := r − b {I}.

• I ∧ r < b ⇒ Q.

• I ∧ r ≥ b ⇒ C ≥ 0.

• {I ∧ r ≥ b ∧ C = T } c := c + 1; r := r − b {C < T }.

The TVT tool veriﬁes algorithms A according to

their speciﬁcation {P} A {Q} in a constructive way

based on semantic tableaux P  ¬wp(A, Q), where

¬wp(A, Q) is the negation of the weakest precondi-

tion of A with respect to Q, which is the ‘weakest’

predicate that ensures that if a state satisﬁes it then

after executing A the predicate Q holds (see (Kalde-

waij, 1990) for more details). For example, we have

the following tableau proof (graphically displayed by

the TVT tool in the right side of Figure 1) to veri-

fy the proof corresponding to the preservation of the

invariant I in the body of the loop: {I ∧ r ≥ b}

c := c + 1; r := r − b {I} ⇔ I ∧ r ≥ b  ¬wp(c :=

c+1; r := r −b, I) ⇔ I ∧ r ≥ b  ¬(I

c+1, r−b

c, r

), where

c+1, r−b

c, r

represents the predicate I in which c and r

are replaced by c + 1 and r − b, respectively (see the

root of the tree in Fig. 1).

To verify and check that this tableau is closed, the

student must press the “Debug” button. The tool then

begins to traverse the tree and tries to locate, for each

of its three branches, a pair of atomic predicates that

are contradictory with the interactive help of the stu-

dent. Beginning with the ﬁrst branch, the student ﬁnds

that b > 0 and b ≤ 0 are contradictory and marks the

branch as “Close”:

Figure 2.

After pressing the button “Next”, the tool ﬁnds in

the second branch two possible atomic predicates that

are contradictory: a = b ∗ c + r and a 6= b ∗ (c + 1) +

(r − b). The student marks the option “Close”:

TVT:ASOFTWAREVERIFICATIONPACKAGEFORTHEINTERACTIVELEARNINGOFFORMAL

PROGRAMMINGTECHNIQUES-AnEducationalExperience

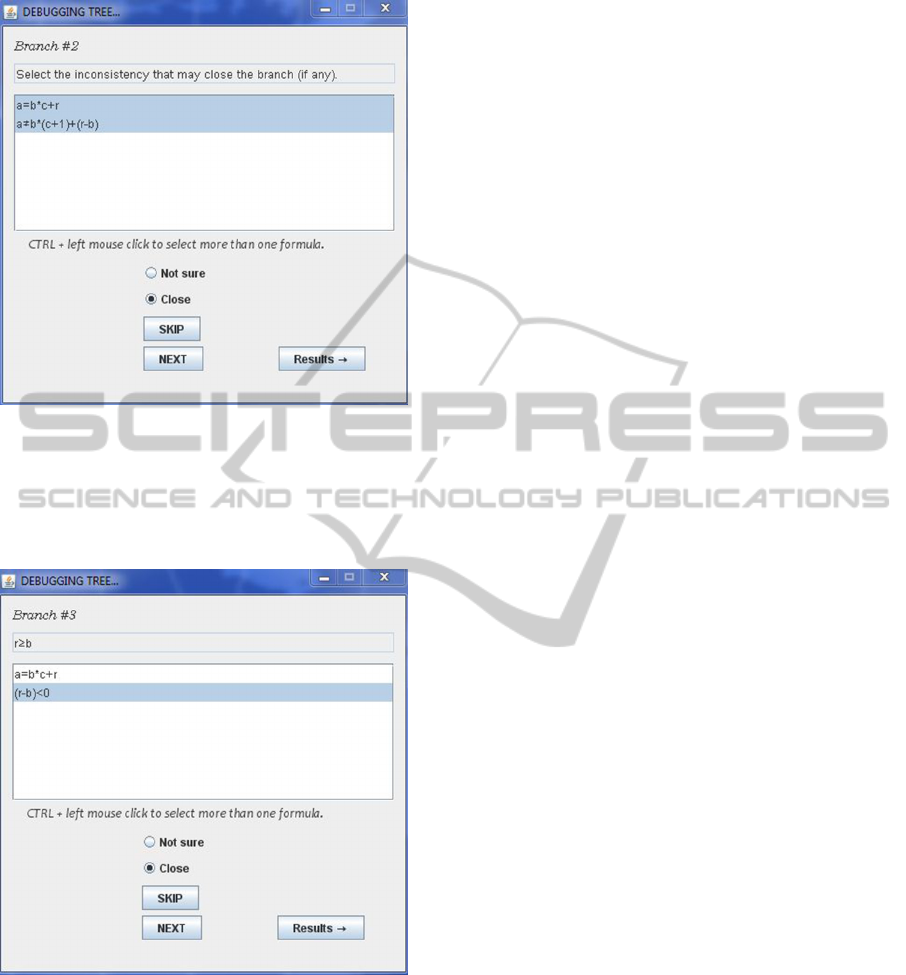
Figure 3.

The tool analyzes the third branch and ﬁnds two

atomic predicates that are contradictory: r ≥ b and

(r − b) < 0. So, the student marks again the option

“Close”:

Figure 4.

Finally, after pressing the button “Results”, the

tool summarizes the conﬂicting atomic predicates that

have found for each of the tableau’s branches. The

formal veriﬁcation session has ﬁnished.

4 ALGORITHMIC DEBUGGING

Debugging is one of the essentials phases of the soft-

ware development cycle and a practical need for help-

ing our students to understand why their programs do

not work as intended. In this section we apply the

ideas of algorithmic debugging (Naish, 1997) as an al-

ternative to conventional approaches to debugging for

imperative programs. The major advantage of algo-

rithmic debugging compared to conventional debug-

ging is that allows our students to work on a higher

level of abstraction. In particular, we have success-

fully applied our TVT tool based on semantic tableaux

for the algorithmic debugging of simple programs to

show how one can reason about such programs with-

out operational arguments. Following a seminal idea

from Shapiro (Shapiro, 1983), algorithmic debugging

proposes to replace computation traces by compu-

tation trees with program fragments attached to the

nodes. As novelty, in this work we propose to use

semantic tableaux as computation trees.

As an example, we alter the code of the previous

algorithm with a simple mistake: we omit the instruc-

tion r := r − b. If we try to verify this erroneous algo-

rithm, we can execute again the TVT tool. If the stu-

dent presses the “Debug” button to start a debugging

session on the proof tree of Figure 1, the TVT tool

tries to close automatically all the possible branches

from the stored information entered in the previous

session. However, since it is not possible to close

the second branch, the tool shows to the student the

predicates a = b ∗ c + r and a 6= b ∗ (c + 1) +r as pos-

sible opposite atoms that should be closed to close

the branch and the proof tree (see the left side of

Figure 5). The user checks that a = b ∗ c + r and

a 6= b ∗ c + (r + b) are not necessarily contradictory

for any value of the divisor b. Therefore, the student

marks the option “Not sure”, and the tool conﬁrms

that this branch cannot be ﬁnally closed and the proof

tree remains open (see the right side of Figure 5).

What failed to close this branch and how it could

be solved? If the student compares again the atomic

predicates previously showed by the tool, a = b ∗ c +

r and a 6= b ∗ c + (r + b), easily concludes that the

expression r + b should be r for every b. But, how

can this be done? Only if the code of the algorithm

executes the instruction r := r − b. By examining the

code, the student discovers that this assignment has

been omitted, and introduces this piece of code into

the body of the loop, because the tool is actually exa-

mining the proof tree {I ∧ B} A {I} corresponding to

this part of the code. After running again the TVT

tool, the student sees that all the proof trees remain

closed. Then, the algorithmic debugging session ﬁ-

nishes.

CSEDU2012-4thInternationalConferenceonComputerSupportedEducation

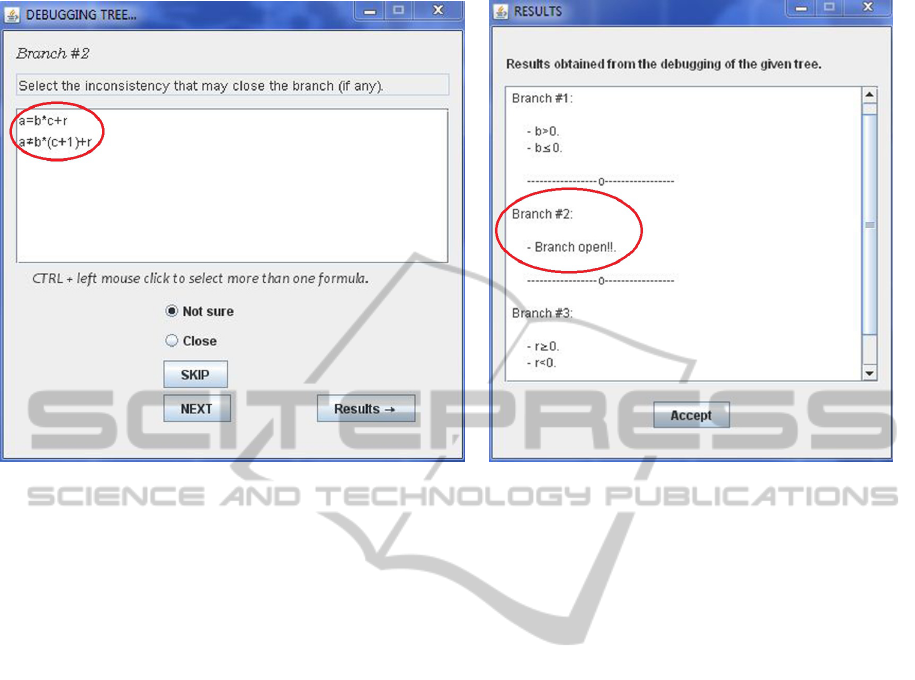
Figure 5: Algorithmic debugging with the TVT tool.

5 EXPERIENCES AND RESULTS

The educational tool TVT is available for the students

of the topics Computational Logic and Design of Al-

gorithms in the Computer Science Faculty of our Uni-

versity through an online educational platform called

Virtual Campus. The following results are based

on the statistics from the 186 students who took the

course in 2009/2010 and 2010/2011.

5.1 Design of the Experiences

We have carried out two educational experiences:

• One non-controlled experience: All the students

may access the Virtual Campus and participate

freely in the experience: download and use the

TVT tool, and answer different tests.

• One controlled experience: Two groups of stu-

dents must answer a test limited in time and ac-

cess to material.

With respect to the non-controlled experience, the

students may freely access the Virtual Campus with-

out any restriction of time or material (slides, bi-

bliography, and the tool) and answer the questions

of several tests. For each of the explained topics in

Computer Science we have provided a test that eva-

luates the knowledge of our students applying diffe-

rent kinds of semantic tableaux. The students may use

these tests to verify their understanding of the diffe-

rent concepts. The questions are structured in three

blocks: propositional and predicate logic, speciﬁca-

tion and veriﬁcation of algorithms, and debugging

and derivation of imperative programs. The resolu-

tion of the tests by the students is controlled by the

Virtual Campus with the help of an interactive tuto-

ring system. In the controlled experience we try to

evaluate more objectively the usefulness of the tool.

In particular we have chosen the application of TVT

for the veriﬁcation and debugging of simple searching

and sorting algorithms (Kaldewaij, 1990). We have

chosen two groups of students answering the same

questions: approximately half of the students works

only with the slides of the course and the books at

class; and the other half works only with the tool at a

Computer Laboratory.

5.2 Results

5.2.1 Non-controlled Experience

We outline here the main conclusions from the re-

sults of the non-controlled experience. With respect

to the material the students used to study, as long as

the exercises were more complicated the use of the

tool (simulations, cases execution, and tool help) in-

creased considerably. Better results were obtained in

the veriﬁcation and debugging of searching and sort-

ing problems (linear and binary search, insertion and

TVT:ASOFTWAREVERIFICATIONPACKAGEFORTHEINTERACTIVELEARNINGOFFORMAL

PROGRAMMINGTECHNIQUES-AnEducationalExperience

correct errors don’t knows

mean σ mean σ mean σ

slides/books 9.36 2.35 6.23 2.37 3.21 2.82

TVT tool 12.77 3.71 4.81 2.10 1.22 1.73

Figure 6: Means and standard deviations (σ).

selection sort). The tool helped our students to vi-

sualize array manipulations in array assignments. In

the rest of the algorithms (slope search and advanced

sorting algorithms) they used only the class material

or bibliography. When answering the tests questions,

the students were also asked whether they needed ad-

ditional help to answer them. In the case of linear

and binary search they used the tool as much as the

class material, which means that visualization of their

own proof tableaux were a useful educational com-

plement. We can conclude that our students consider

the tool as an interesting resource and have used it to

complement the rest of the available material.

5.2.2 Controlled Experience

The controlled experience was carried out with 59

students. We gave 32 of them only the slides of the

course and the books of the bibliography (Fitting,

1990; Kaldewaij, 1990). The rest were taken to a

Computer Laboratory, where they could execute the

TVT tool. We gave the same test to both groups, con-

sisting of 18 questions, 12 of them on speciﬁcation

aspects of the algorithms (inference of invariants and

bound functions), and the rest on their veriﬁcation and

debugging from the code. In Figure 6 we provide the

means and the standard deviations of correct, errors,

and don’t knows answers. First, we observe that stu-

dents using TVT answer more questions than the other

ones. In addition, they make less errors than the o-

thers. This is due to the fact that most of the students

of the TVT tool group performs the analysis of the

algorithms directly from the corresponding semantic

tableau displayed by the tool, while the slides/book

group has to hardly deduce it directly from the code.

All the students who used TVT indicated the bene-

ﬁts of using tableaux to understand the code of the

algorithms from their speciﬁcations. Therefore, we

can conclude that the methodology proposed in this

work constitutes a good complement to facilitate the

comprehension of the design and analysis of impe-

rative programs. In addition, the methodology based

on tableaux has helped us to detect in the students dif-

ﬁculties applying the formal techniques to derive cor-

rect and efﬁcient imperative programs from speciﬁca-

tions.

6 CONCLUSIONS

We have presented the educational and interactive tool

TVT based on semantic tableaux for a speciﬁcation

language on predicate logic to perform veriﬁcation

and debugging of algorithms. This is a ﬁrst step to-

wards the development of a practical teaching tech-

nology for the formal learning of programming tech-

niques.

We have systematically evaluated the proposed

methodology to conﬁrm that TVT is a good comple-

ment to both the class explanations and material, ma-

king easier the visualization of proofs in the reason-

ing needed for the design of correct and efﬁcient pro-

grams. We look forward to making good use of what

we have learned from this evaluation to improve tool’s

usefulness in Computer Science Education.

REFERENCES

Dijkstra, E. (1976). A Discipline of Programming. Prentice

Hall.

Fitting, M. (1990). First-Order Logic and Automated The-

orem Proving. Springer, Graduate Texts in Computer

Science.

Huertas, A. (2011). Ten years of computer-based tutors

for teaching logic 2000-2010: Lessons learned. In

TICTTL.

Kaldewaij, A. (1990). Programming: The Derivation of Al-

gorithms. Prentice-Hall International Series in Com-

puter Science.

Naish, L. (1997). A declarative debugging scheme. Journal

of Functional and Logic Programming, vol. 3.

Shapiro, E. (1983). Algorithmic Program Debugging. MIT.

van ditmarsch, H. (2005). Logic software and logic educa-

tion.

CSEDU2012-4thInternationalConferenceonComputerSupportedEducation