A COMPRESSED DATA MODEL FOR A BITMAPPED XML

STRUCTURE

Mohammed Al-Badawi

Department of Computer Science, Sultan Qaboos University, Muscat, Oman

Keywords: PACD XML Technique, XML Processing, XML Compression, XML Clustering, Sparse Matrix

Compression, Bitmap Storage.

Abstract: Developments on XML processing usually produce tools to formulate both the XML data storage and the

associated query processor. PACD is one of such developments that stores the XML structure into a set of

n×n bitmap matrices each of which encodes a specific XML structure related to an XPath axis. The amount

of space and the complexity of storing uncompressed version of these matrices is large for huge XML

databases; and such requirements may go beyond the HW/SW capabilities; this justify the need for the data

compression model discussed in this paper.

1 INTRODUCTION

PACD, as a new bitmapped XML processing

technique, was initially introduced in (Al-Badawi et

al, 2009). The technique encodes the entire XML

structure into ten bitmap matrices each of which

corresponds to a certain XPath (Berglund et al.,

2010) axis. This paper discusses the specifications of

the data compression model (DCM) used by PACD

to reduce the amount of the storage space required

for storing the XML structure. The DCM illustrated

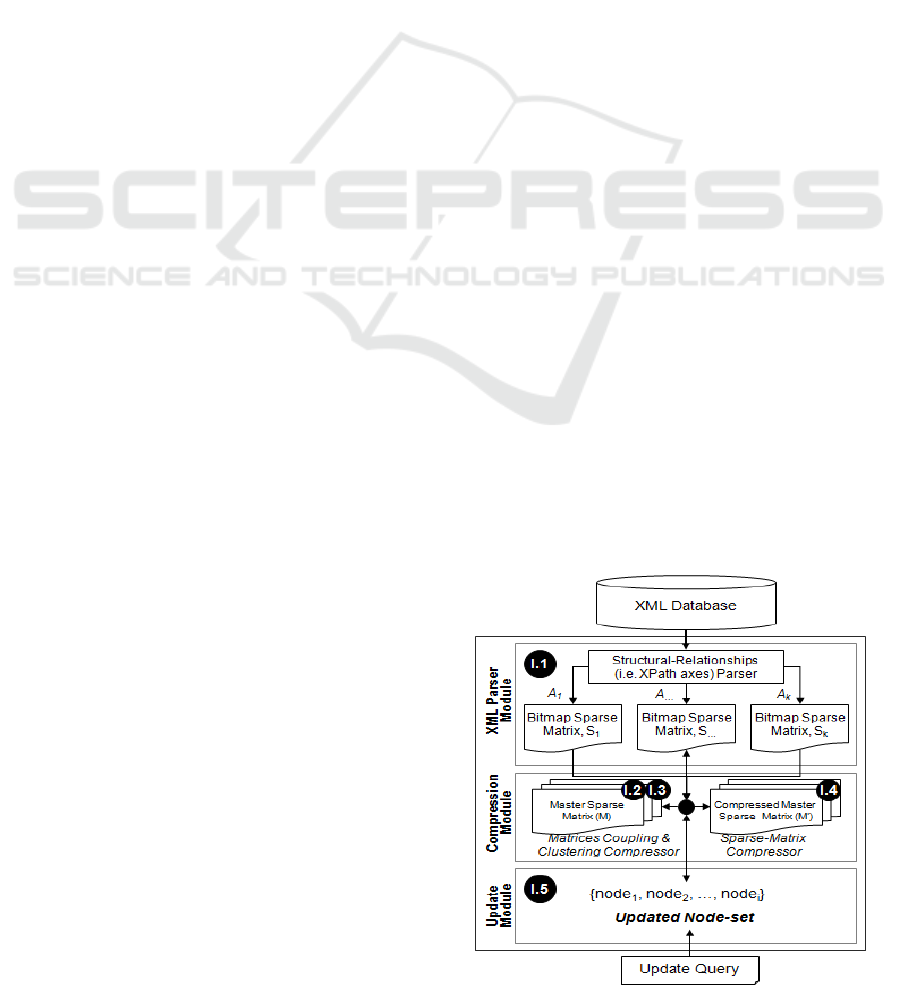
in Fig. 1, performs three compression processes to

the XML structure (labelled by I.2, I.3 and I.4 in Fig.

1) in order to reduce its complexity in terms of

storage requirements, representations layout and

data manipulations. The first process reduces the

number of the matrices encoded from ten to five

matrices by using a simple matrix transformation

algebra which facilitates 2-in-1 representations for

some related matrices. The second compression

process provides a method by which two or more

matrices can be combined into a single matrix called

a ‘master’ matrix. The process may generate

multiple master matrices which should preserve

specific characteristics of their composing matrices.

The third process is the sparse-matrix compression

process which employs one or more sparse-matrix

compression techniques to act over the master

matrices in order to compact their physical

representations. The sparse-matrix compression

should allow the compressed data to be managed

efficiently during the course of the query execution

and data update transactions.

The rest of this paper is organized as follows.

Section 2 briefly restates the specifications of PACD

and its data representation in Sections 2.1 and 2.2

respectively. The need for the proposed DCM is

justified in Section 2.3 while Section 3 discusses the

specifications of the PACD’s DCM including the

three compression processes that are performed over

the encoded XML structure. The paper is concluded

in Section 4.

Figure 1: PACD’s Index Builder (IB).

Al-Badawi M..

A COMPRESSED DATA MODEL FOR A BITMAPPED XML STRUCTURE.

DOI: 10.5220/0003895400890095

In Proceedings of the 8th International Conference on Web Information Systems and Technologies (WEBIST-2012), pages 89-95

ISBN: 978-989-8565-08-2

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 BACKGROUND

2.1 PACD Technique

PACD, introduced in (Al-Badawi et al, 2009), is a

bitmap XML processing technique consists of two

subsystems: the Index Builder (IB) and the Query

Processor (QP). The IB shreds XML data (including

the textual contents and the XML structure) into the

underlying data storage while the QP translates and

executes XML queries (expressed in XQuery

syntax) over the shredded XML data. Of the former,

the component performs three main operations

including the conversion of XML structural

relationships into a set of binary relations (bitmap

format), the compression of bitmapped XML

structure and the XML updates handling (see Fig 1).

During the first operation (process I.1 in Fig. 1), the

XML structural relationships (derived by the

XPath’s thirteen axes and their extension; the Next

and Previous axes(Al-Badawi et al, 2009) are

organized into a set of n×n matrices each is

representing a specific XML structure corresponding

to an XPath axis. The entries of the generated

matrices are binary where ‘1’ is indicating the

existence of the structural relationship (e.g. child,

parent, …etc) while ‘0’ is indicating the absence of

such relationship between any node pairs (Wang et

al., 2006; He et al., 2005). In the XML databases

context, these matrices are sparse (Sun et al., 2008;

George et al., 1993) and their dimensions are huge

can go beyond any hardware and software limits.

This justifies the need of the proposed Data

Compression Model (DCM).

2.2 Encoding XML Structure in PACD

As mentioned above, PACD explicitly encodes the

whole XML structure represented by XPath axes

into a set of bitmap matrices . Two main advantages

of such encoding are: a) to increase the QP coverage

and b) to reduce the overhead workload caused by

deriving some XML structures from others

(Pettovello and Fotouhi, 2006).

XPath/XQuery (Berglund et al., 2010; Boag et

al., 2010) specification describes 13 axes for any

context node in the XML tree. These are the self,

child, parent, descendant, self-or-descendant,

ancestor, self-or-ancestor, preceding, following,

preceding-siblings, following-siblings, attributes and

namespace axes. Additionally, PACD introduced the

‘next’ and ‘previous’ axes to substitute the

following-sibling and preceding-sibling in

preserving the document order (Al-Badawi et al,

2009). The process of mapping XML structure into

bitmap matrices explicitly excludes the ‘namespace’

axis due its popularity in XML database

transactions, combines the ‘self-or-descendant’ with

the ‘descendant (and ‘self-or-ancestor’ with the

‘ancestor) into a single matrix respectively, and

encodes attributes as ordinary child-entries in all

matrices. Furthermore, PACD deals with the ‘self’

axis at the XML processing level (i.e. querying and

updating) instead of encoding this structure

explicitly in a separate matrix

As for illustration, Fig. 2 depicts a sample XML

database while Fig. 3 and Fig. 4 respectively show

the childOf and descendentOf matrices for the XML

tree as an example of the XML/matrix

transformation.

<dblp>

</book>

<last>Smith</last>

</book>

</thesis>

</dblp>

Figure 2: An XML database example.

2.3 The Need for Data Compression

It is clear from the above discussion that the size of

the PACD’s data storage for large XML databases

will be huge in terms of matrix dimensions and

physical storage space. This could result in several

performance issues such as HW/SW failure and

processing deficiencies. One way to overcome such

limitation is to have the PACD’s data storage

reduced by the all means while keeping its XML

structure coverage still comprehensive.

A such proposal can also benefit the following

aspects:

¾ Memory Based Management: is an attractive

approach since it eliminated overhead caused by

perform I/O operations. To achieve this, XML

literature has produced different data compression

techniques including data guide summaries

(Goldman and Widom, 1997; Haw and Lee, 2009),

adaptive indexes (Chung et al., 2002), and selective

indexes (Milo and Suciu, 1999; Hammerschmidt,

2005). The compression architecture of these

techniques takes place at the XML encoding level

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies







&0 &1 &2 &3 &4 &5 … &11

&0000000…0

&1100000…0

&2010000…0

&3010000…0

&4100000…0

&5000010…0

………………………

&11000000…0













&0 &1 &2 &3 &4 &5 … &11

&0000000…0

&1100000…0

&2110000…0

&3110000…0

&4100000…0

&5100010…0

………………………

&11100000…0







Figure 3: The childOf Matrix. Figure 4: The descendentOf (or descOf) Matrix.

Figure 5: The framework of the PACD’s data compression model for the XML structure.

rather than the data representation level which in

turn results in some other performance issues such

as summary expressiveness. PACD redeems such

shortcoming by encoding the full XML structure and

incorporates well established compression

techniques to reduce the size of encoded

information.

¾ Database Sizing: In this context, database

sizing describes the process of controlling the size of

the database in order to utilize the computer

system’s resources during the database management

(McCord, 1981; O’Neil and O’Neil, 2001). Loading

‘x’ storage units (e.g. byte) is often faster than

loading ‘x+y’ storage units (N.B.: other factors, such

as the desirable data location, are also involved but

the same logic applies). Therefore, there is no doubt

that the compressed data will outperform the un-

compressed data provided that the same database’s

functionalities are obtainable from both versions,

and the data compression complexity is kept to the

minimum.

¾ Nature of Data Presentation: Finally, the

amount and type of information stored by PACD

necessitates the use of data compression techniques.

PACD aims to store the XML structures using a

bitmap based representation which is encoded into

sparse-matrices. The system creates ten sparse

matrices (see next section) for this purpose, each of

which requires ‘n×n’ storage units. The total figure

for storing these matrices, as well as XML’s textual

contents, becomes huge for large XML databases

and could be beyond the capabilities of the

ACOMPRESSEDDATAMODELFORABITMAPPEDXMLSTRUCTURE

underlying hardware and software specifications; or,

it could result in other performance issues.

3 A DATA COMPRESSION

MODEL

To achieve a better data storage performance PACD

maintains separate models for compressing the XML

textual contents and the XML structure respectively.

This paper only describes the mechanism used to

compress the XML structure.

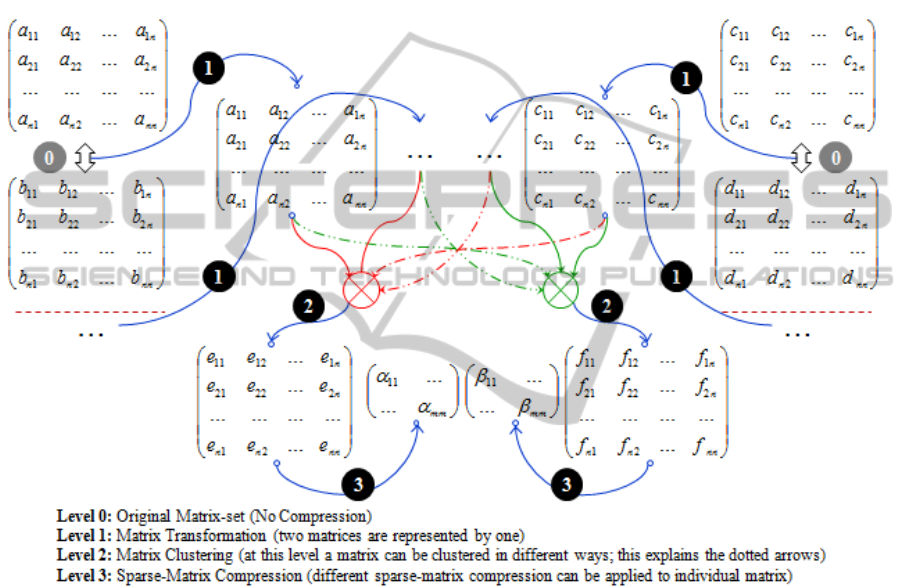
3.1 Model Overview

The PACD’s matrix based storage (or XML

structure storage) can be compressed using three

different types of matrix operations. These are

matrix transformation operations to derive some

matrices from other matrices; matrix clustering

operations to combine a set of matrices into one

matrix; and sparse-matrix compression techniques to

further reduce the storage space requirement of the

final matrix set. The layout of the overall XML

structure compression is illustrated in Fig. 5 while

each of these levels is briefly described in the

subsequent sections.

3.2 A Matrix Algebra

To formulate data compression model transactions,

each matrix will be represented as a set and the

group of sets are then manipulated (e.g. transformed)

using set-theory notations. A set, corresponding to a

specific PACD’s matrix, contains the positive entries

of that matrix encoded as node pairs. For example,

the entries of the childOf set of the above XML tree

are {(&1,&0), (&4,&0), (&9,&0), (&2,&1), …,

(&11,&9)}.

On the other hand, XML structures reflected by

the thirteen XPath’s axes and their extensions the

‘next’ and ‘previous’ axes, are encoded into ten

sparse matrices as proposed earlier. According to the

XPath’s specification (Berglund et al., 2010), these

axes are found in invertible and/or inclusive pairs

and hence their sparse-matrix and set

representations. Based on this logic, the first

compression level of the bitmapped XML structure

uses the invertible characteristic of the XML

structure in order to reduce the number of matrices

explicitly encoded in the underlying storage while

the second level of the compression uses the

inclusive characteristics to combine two or more

matrices into a single matrix. The following two

sections formulate the first two compressions while

the third compression process is described then after.

3.3 Invertible-matrix Transformation

Invertible XPath’s axes are those axes which their

XML structural relationships are the inverse of each

other. There are five axis-pairs of this type; the

child, descendent, following, following-sibling and

next axes are the inverse of the parent, ancestor,

preceding, preceding-sibling and previous axes

respectively. The notion of compression in this level

is to encode (consider) only one axis of each axis-

pair in the underlying data storage while the image-

axis can be calculated using simple geometric

transformations on the set (or matrix) representation

of the corresponding XML structure. Thus, the

number of matrices (sets) that need to be encoded in

the underlying data storage is reduced from ten to

five only which in turn halves the amount of storage

space required for the entire XML structure.

As for illustration, the childOf and parentOf

matrices can be algebraically calculated from each

other using the formula childOf[i,j] = parentOf[j,i].

In terms of geometric transformation, the parentOf

matrix can be obtained by rotating the childOf

matrix by 90° clockwise and then reflecting the

matrix on the y-axis. In practice this is simply done

by inverting the first matrix indices to obtain the

entries of the second matrix. The five possible

geometric transformation of XPath’s axes are

formulated in Fig. 6.

3.4 Matrix Clustering

Invertible-matrix transformation were only able to

reduce the number of encoded matrices (XML

structure) from ten to five matrices. Therefore, the

amount of storage space required to store the five

matrices remains big for large XML databases. This

necessitates advances in storage space reduction

which could be achieved by further reduction in the

number of matrices and/or using sophisticated

compression algorithms to store the matrices inside

the computer’s storage media.

In this context, the matrix clustering process

maps the corresponding entries of two or more

matrices to a single entry producing a matrix which

represents the all combined matrices. To do so, two

conditions must apply. Firstly, all combined

matrices must have the same degree of rows and

columns. Secondly, entries of all combined matrices

must have a finite set of values; in other words,

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

anceOfMdescOf

anceOf

descOf

⎯→⎯⎯→⎯Φ

° '

|90

precOfMfollOf

precOf

follOf

⎯→⎯⎯→⎯Φ

° '

|90

recSibO

MfollSibOf

precSibOf

follSibOf

⎯→⎯⎯→⎯Φ

° '

|90

prevOfMnextOf

prevOf

nextOf

⎯→⎯⎯→⎯Φ

° '

|90

Figure 6: Invertible Transformations of the XML

Structure.

SSdescOfchildOf

descOfchildOf

≤⇒⊆

SSanceOfparentOf

anceOfparentOf

≤⇒⊆

SSprecOfprecSibOf

precOfprecSibOf

≤⇒⊆

SSfollOffollSibOf

follOffollSibOf

≤⇒⊆

SSprecSibOfprevOf

precSibOfprevOf

≤⇒⊆

SSfollSibOfnextOf

follSibOfnextOf

≤⇒⊆

childOfchildOfdescOf

descOfchildOfdescOf

=⇒

=∩

⊕

1−+=⇒

=∩

⊕

ooo

SSS

nextOfchildOf

nextOfchildOfnextOfchildOf

1−+=⇒

=∩

⊕

ooo

SSS

nextOfdescOf

nextOfdescOfnextOfdescOf

S° is the sparsity-degree of the matrix A; calculated by

dividing the number of non-zero elements by n

⊕ is the addition operation (clustering) of two matrices

Figure 7: More XML structure semantic based on

Matrix/Set representation.

entries must have limited domain of values and the

domains must be identical; e.g. {0, 1} or {a, b, c} for

all matrices. The value of the [i,j]

entries from all

matrices are combined somehow to produce the

[i,j]

entry in the resulting matrix. For example, if

we have two matrices A and B such that A[i,j] ∈

{0,1} and B[i,j] ∈ {0,1}, then we can use ‘0’, ‘a’,

‘b’ and ‘c’ to respectively map ‘00’, ‘01’, ‘10’ and

‘11’. The resulting matrix, say C, will then have

entries all belong to {0,a,b,c} (i.e. ∀ c

∈ C; C[i,j] ∈

{0,a,b,c}). We call output matrix a Master matrix

and its degree (i.e. dimension) must be the same as

the composing matrices.

In the PACD’s data representation, the above

two conditions are imbedded in the PACD’s storage

specifications (see Section 2.2). So, all matrices

generated are of power ‘n×n’, and the entries of

these matrices have either ‘0’ or ‘1’ values.

Complexity-wise, the cost of the clustering

process itself is determined by the size of the values’

set and the number of clustered matrices. In practice,

the complexity is found low because the process

may cluster a maximum of five matrices with only

two possible values ‘0’ or ‘1’. However, the matrix

clustering process should also consider the trade-off

between the storage space reduction and the

performance issues that incurred by the querying and

updating processes. Due the space limitation, the

discussion of this topic is omitted from this paper.

In general, the clustering process is guided by the

set-based XML semantic listed in Fig. 7. Fig. 8

provides an example of clustering the child and

descendent matrices using a simple-clustering table.

Case 1 Case 2 Case 3

Case 4

childOf (A) 0 0 1 1

descOf (B) 0 1 0 1

A&B

‘00’ ‘01’ ‘10’ ‘11’

ƒ(A & B)

0 1 2 3

* Impossible case (see Fig. 6)







&0 &1 &2 &3 &4 &5 … &11

&0000000…0

&1300000…0

&2130000…0

&3130000…0

&4300000…0

&5100030…0

………………………

&11100000...0







924.0=

childOf

854.0=

descOf

854.0=

⊕

descOfchildOf

Figure 8: A clustering example (childOf ⊕ descOf).

3.5 Sparse-matrix Compression

The maximum compression degree of the first two

levels can reduce the storage requirement of storing

k number of matrices (corresponding to a single

XML tree of size ‘n’ nodes) up to n

storage units.

This remains an issue for large XML databases and

multi-document XML databases, where the value of

‘n’ is high with respect to the available system’s

resources. For example, a tree of 10

nodes requires

bytes (≅1000 GB) when each matrix’s entry is

stored using 1-byte storage. Thus, this justify the

need for an additional compression level which acts

on the resulting matrices considering their unique

characteristics; e.g. the sparsity-degree and the

zero’s distribution.

“A matrix is sparse if many of its coefficients are

zero … (and) … Generally, we say that a matrix is

parentOfMchildOf

parentOf

childOf

⎯→⎯⎯→⎯Φ

° '

|90

ACOMPRESSEDDATAMODELFORABITMAPPEDXMLSTRUCTURE

sparse if there is an advantage in exploiting its

zeros” (Duff et al., 1986). In (George et al., 1993), a

sparse matrix is also defined as the matrix which is

populated mainly with zeros whiles some references

are more specific, limiting the definition to those

matrices with certain amount of 0’s; e.g. 50% of the

entries are 0 as in (Mackay and Neal, 1995).

According to the above, our matrices for

representing the XML structures are considered to

be sparse. This is mainly reflected by the analysis

given in (Al-Badawi, 2010) which shows that the

number of zeros in the childOf and nextOf matrices

reaches n

-n, and the numbers of zeros in the descOf

matrix may exceed n

-h×n where ‘n’ is the number

of nodes and ‘h’ is the number of levels in the

underlying XML tree. When n goes high, the

number of 0 entries easily exceeds 90% of the total

entries

From a technical point of view, storing matrices

of this size in the computer system is a trade off

between the high storage size and storage

performance (Tarjan and Yao, 1979). For example,

to store a matrix when n=10

into two-dimensional

array of type character (one byte stores one

character), we need 10

bytes of memory which

may defeat the HW/SW capabilities. One way to

address this issue is using sparse matrix compression

(SMC) techniques to compact the matrix’s storage.

The architecture of any SMC technique depends

on the computation to be performed, the pattern of

the non-zero entries, and even the architecture of the

computer system itself (Duff et al., 1986; Willcock

and Lumsdaine, 2006). Among these three factors,

we are only concerned with the computation

constraints in this stage of our research; having that

achieving optimum storage with good performance

is the main goal of the compression process. The

investigation of other issues is a subject for further

research.

To align the choice of the used SMC with the

cost reduction of the XML querying and updating

operations, PACD categorizes the existing sparse-

matrix techniques into two groups; the first includes

the techniques which do not necessitate any

decompression/recompression process during the

XML querying and updating operations so the

overhead complexity incurred by these processes

will be avoided during the XML querying and

updating. The second category contains those

techniques which defeat the XML operations by the

cost of decompressing/recompressing processes

done to the underlying storage. Detailed discussion

of this aspect plus the empirical proof lays down

outside the scope of this paper due the space

limitation.

4 CONCLUSIONS

To conclude, this paper described the PACD’s DCM

which uses three data compression processes to

compact the XML structures. As introduced in (Al-

Badawi et al., 2009), the XML structures are

theoretically encoded into ten n×n matrices each of

which represents a structural relationship which

corresponds to an XPath’s axis or an extension. Each

structural relationship is encoded into a set of node

pairs where such relationship applies between them.

So, each matrix represents the corresponding

structural relationship between all nodes in the XML

tree.

PACD’s matrices are found in invertible pairs

and inclusive pairs, and are sparse. The first

compression phase uses the first characteristic; that

is each invertible pair is represented by only one

matrix. This process can reduce the number of

matrices from ten to five matrices. The next

compression phase uses the inclusiveness

characteristic; that is two or more matrices are

clustered into a single matrix such that the full

architecture of all composing matrices is preserved

in the clustered matrix. The last compression phase

is based on using one or more sparse-matrix

compression techniques to compact the layout of the

resulting matrix from the first two compressions.

The strength and efficiency of the PACD’s

overall storage is determined by the specification of

the clustering and SMC methods used. A complete

discussion about this topic including the

experimental proof is the subject for further

publications.

REFERENCES

Al-Badawi, M. (2010) ‘A Performance Evaluation of a

New Bitmap-based XML Processing Approach’, PhD

Thesis, University of Sheffield, UK.

Al-Badawi, M., Eaglestone, B., and North, S. (2009)

‘PACD: A Bitmap-based Framework for Processing

XML Data’, In the proceedings of the WebIST’09,

Lisbon, Portugal, pages 66-71.

Berglund, A., Boag, S., Chamberlin, D., Fernández, M.,

Kay, M., Robie, J., and Siméon, J. (2010) XML Path

Language (XPath) 2.0 (2

Ed.), [Online] Avail: http://

www.w3.org/TR/xpath20/ [15/11/2011].

Boag, S., Chamberlin, D., Fernández, M., Florescu, D.,

Robie, J., and Siméon, J. (2010) XQuery 1.0: An XML

Query Language, (2

Ed.) [Online] Avail: http://www

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

.w3.org/TR/xquery/ [15/11/2011].

Chung, C., Min, J., and Shim, K (2002) ‘APEX: An

Adaptive Path Index for XML Data’, In proceedings

of the 2002 ACM SIGMOD international conference

on Management of data, Madison, Wisconsin, pages

121-132.

Duff, I., Erisman, A., and Reid, J. (1986) Direct Methods

for Sparse Matrices. Oxford University Press, New

York and London.

George, A., Gilbert, J., and Liu, J. (1993) Graph Theory

and Sparse Matrix computation, Volume 56 of the IMA

volumes in Mathematics and its Applications, Volume

56 of Partially Ordered Systems. Springer-Verlag.

Goldman, R., and Widom, J. (1997) ‘DataGuides:

Enabling Query Formulation and Optimaization in

Semistructured Database’, In proceedings of the 23

international conference on VLDB, pages 436-445.

Hammerschmidt, B. (2005) ‘KeyX: Selective Key-

Oriented Indexing in Native XML Databases’, PhD

Thesis Published. in: Dissertations in Database and

Information Systems - Infix, Volume 93, ISBN

1586035894.

Haw, S., and Lee, C. (2009) ‘Extending path summary and

region encoding for efficient structural query

processing in native XML databases’, Journal of

Systems and Software, Volume 82, Issue 6, pages

1025-1035.

He, H., Wang, H., Yang, J., and Yu, P. (2005) ‘Compact

Reachability Labeling for Graph-Structured Data’, In

proceedings of the 14

ACM international conference

on Information and knowledge management, Bremen,

Germany, pages 594-601

Mackay, D., and Radford, N. (1995) ‘Good Codes based

on Very Sparse Matrices’, Lecture notes in Computer

Science, Volume 1025/1995, pages 100-111.

McCord, R. (1981) ‘Sizing and Data Distribution for a

Distributed Database Machine’, In proceedings of the

1981 ACM/SIGMOD international conference on

Management of Data, Michigan, USA, pages 198-204.

Milo, T., and Suciu, D. (1999) ‘Index Structures for Path

Expressions’, In proceedings of the 7

International

conference on Data Technology, Volume 1540/1998,

Jerusalem, pages 277-295.

O’Neil, P., and O’Neil, E. (2001) ‘Database: Principles,

Programming, and Performance’, Morgan Kaufmann

Publishers, 2

Edition, 2001.

Pettovello, P., and Fotouhi, F. (2006) ‘MTree: An XML

XPath Graph Index’, ACM/Sym. on Applied

computing, Dijon, France, pages 474-481.

Sun, J., Xie, Y., Zhang, H., and Faloutsos, C. (2008) ‘Less

is More: Sparse Graph Mining with Compact Matrix

Decomposition’, Journal of Statistical Analysis and

Data Mining, Volume 1, Issue 1, pages 6-22.

Tarjan, R., and Yao, A. (1979) ‘Storing a Sparse Table’,

Journal of Communications of theACM, Volume 22,

Issue 11, pages 606-611.

Wang, H., He, H., Yang, J., Yu, P., and J Yu. (2006) ‘Dual

Labeling: Answering Graph Reachability Queries in

Constant Time’, In the proceedings of the

International conference of Data Engineering, pages

75-86.

Willcock, J., and Lumsdaine, A. (2006) ‘Accelerating

Sparse Matrix Computations via Data Compression’,

In proceedings of the 20

international conference on

Supercomputing, Queensland, Australia, pages 307-

316.

ACOMPRESSEDDATAMODELFORABITMAPPEDXMLSTRUCTURE