
EDUSOFT PACKAGE FOR STRUCTURAL ENGINEERING
Web-based Educational Material using JAVA for Structural Dynamics
C. G. Panagiotopoulos
1
, G. D. Manolis
2
and A. Athanatopoulou
2
1
Department of Continuum Mechanics, University of Seville, Camino de los Descubrimientos, Seville, Spain
2
Department of Civil Engineering, Aristotle University, Panepistimioupolis, Thessaloniki, Greece
Keywords:
Structural Dynamics, Web-based Applications, Single Degree-of-freedom Systems, Multiple Degree-of-
freedom Systems, Modal Analysis, Time History Analysis, Earthquake Spectra, Multi-story Buildings.
Abstract:
In this work, we present the construction of an integrated, web-based software package offering structural dy-
namics analysis capabilities for use by both undergraduate and graduate students in civil engineering programs
who specialize in earthquake engineering. The software package is built on a Java platform and comprises five
modulus, focusing on the analysis of single and multiple degree-of freedom systems, modal analysis of 2D
and 3D frames, and earthquake spectra construction.
1 INTRODUCTION
Greece is the most earthquake-prone country in the
EU, so infrastructure built must conform in terms of
structural design to the European code EC8 (CEN,
2004). To this end, Civil Engineering departments in
Greece have been offering courses in structural dy-
namics and earthquake engineering (Chopra, 2007)
since the 1980’s. Two difficulties are encountered
here: (i) students must have a good structural analysis
background from past semesters and (ii) any mean-
ingful examples that must be worked out carry a large
volume of computation, often necessitating the use of
finite element packages that turns out to be cumber-
some because the structure has to be modelled a pri-
ori.
In this work, we develop versatile, easy to use ed-
ucational tools for solving problems in structural dy-
namics. The web turns out to be the preferred way
of access by setting up a dedicated electronic address
as http://edusoft.civil.auth.gr, “edusoft” being an um-
brella address containing a number of application pro-
grams. Access to “edusoft” is free, unlimited and
applications are open-source under the GPL license,
which obviates the need to register users and at the
same time precludes unauthorized external use. Un-
der code numbers TE1800 and TE 2400 for the Dy-
namics of Structures I and II courses, we have the five
modules (“jesdof”, “espec”, “jframe”, “jsisma” and
“jTframe”) described herein. Once accessed, the en-
vironment is interactive and good quality graphs as
as well as real time animation of the response are
produced. We note that a Java runtime environment
(JRE) has to be activated in the receiving computer
for the programs to function (Gosling et al., 2005),
and the language of application is Greek.
It should be mentioned here that development
of educational packages on various types of elec-
tronic platforms is an ongoing activity. As exam-
ples, we mention diverse work ranging from that of
(Katsanos et al., 2011) on seismic design of rein-
forced concrete buildings based on the Matlab plat-
form for professional engineers and that of (Sobha-
ninejad et al., 2011) on integrated earthquake simula-
tion comprising hazard quantification, disaster quan-
tification and post-earthquake recovery for use by
government agencies and planners.
Finally, two object-oriented, open source software
frameworks that create both parallel and serial finite
element computer applications for structural response
to dynamic loads such as earthquakes are OpenSees
(http://nees.org) and Nemesis (http://www.nemesis-
project.org) projects. These platforms are written in
C++ and utilize Fortran numerical libraries as well
as interpreted/scripting languages (i.e., Tcl, Pyhton,
etc.). However, the scale of computation and model-
ing details are vastly higher compared to our work,
and requires from the user competence in dynamic
structural analysis.
299
G. Panagiotopoulos C., D. Manolis G. and Athanatopoulou A..
EDUSOFT PACKAGE FOR STRUCTURAL ENGINEERING - Web-based Educational Material using JAVA for Structural Dynamics.
DOI: 10.5220/0003901402990303
In Proceedings of the 4th International Conference on Computer Supported Education (CSEDU-2012), pages 299-303
ISBN: 978-989-8565-07-5
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 SDOF MODULE “JESDOF”
The most fundamental concept in structural dynam-
ics is the single degree-of-freedom (SDOF) oscilla-
tor, whose understanding is crucial for students. This
was the rationale behind the development of software
module “jesdof”. More specifically, four subcate-
gories of data must be defined: (a) elastic proper-
ties (stiffness), mass and energy-loss (damping); (b)
initial conditions for the displacement and velocity;
(c) definition of the external source of excitation (dy-
namic loading), either as an ASCII file containing dis-
crete values at equally spaced time intervals, or by a
mathematical expression; and (d) parameters associ-
ated with the time integration algorithm used to nu-
merically solve the governing differential equation of
the system.
The governing differential equation for dynamic
equilibrium is
m¨x(t) + c˙x(t) + kx(t) = F
0
f(t) (1)
where m, c, k are the mass, damper, and stiffness (in
tons, kN-sec/m and kN/m, respectively) of the struc-
tural system, while x(t) (in m) is its response to a
dynamic load of magnitude F
0
(in kN) and dimen-
sionless time variation f(t). Note that overdots de-
note derivatives with respect to time t. Furthermore,
the natural frequency and fundamental period of the
SDOF system are ω
2
0
= k/m, T = 2/ω
0
(in rad/sec and
sec, resp.). It is standard practice to define a dimen-
sionless damping ratio ζ = c/2mω
0
in lieu of damper
values. Finally, the closed form solution of the SDOF
is given by Duhamel’s integral as
x(t) = x
0
cos(ω
0
t) + ( ˙x
0
/ω
0
)sin(ω
0
t) +
x
ST
ω
0
Z
t
0
f(t)sin
ω
0
(t − τ)
dτ (2)
where x
0
, ˙x
0
are initial displacement and velocity of
the system, while x
ST
= F
0
/k is its equivalent static
displacement. For ground accelerations ¨x
g
(t), the
forcing function becomes F(t) = −m¨x
g
(t) and the
SDOF kinematics are understood to be relative to the
ground motion. Solution is accomplished through nu-
merical integration of Eq. 2 using the Newmark beta
algorithm, with the time interval of interest subdi-
vided into N increments of size equal to or less than
T/10. The structural response is given in a simple
text area. Finally, the user may visualize the motion
of the system in the graph area of the GUI by select-
ing as abscissa and ordinate variables in combination:
time, external force, displacement, velocity and accel-
eration.
3 RESPONSE SPECTRA “ESPEC”
This application produces elastic response spectra
from ground motion recordings, defined as the plot
of maximum response (for either kinematic or force
variables) versus frequency (or period) of all possi-
ble SDOF systems under a specific type of external
force (usually a seismically-induced ground motion).
More specifically, response spectra are parametric in
terms of damping (e.g., ζ = 0− 10%) and are com-
puted from Duhamel’s integral of Eq. 2 by varying
the natural period of an SDOF system so as to sweep
an acceptable range that corresponds to real struc-
tures, i.e., 0 ≤ T ≤ 3.0 (in sec). Following computa-
tion, the results may be presented as absolute pseudo-
acceleration, relative pseudo-velocity or relative dis-
placement related as
S
A
= ωS
V
= ω
2
S
D
(3)
The above an exact relation for a damping ratio of
zero and approximate otherwise. Module “espec” uti-
lizes the Newmark-beta numerical integration algo-
rithm for integrating the equation of motion in time.
4 3-STORY FRAME “JFRAME”
Application module “jframe” does modal analysis of
a simple three story plane frame that translates into a
three DOF system, whose properties are user defined
as the elastic and inertial characteristics plus the ge-
ometrical configuration. Upon entering the input pa-
rameters, this program module computes and presents
in simple text area the following fundamental data:
stiffness matrix, mass matrix, period and frequency
associated with each eigenmode, the components for
each eigenvector, plus the participation factor, gener-
alized mass and effective mass corresponding to each
eigenmode. The underlying computation procedures
are based on the finite element method, but this does
not require any detailed knowledge from the part of
the students. Finally, there is an option to specify
an acceleration response spectrum, in which case the
program proceeds to calculate the spectral pseudo-
acceleration, relative pseudo-velocity and the relative
displacement for each eigenmode. More specifically,
the governing equation of motion for a multiple DOF
system is Eq. 1 again, except that the quantities of
interest are now matrices and vectors (of size N, the
number of independent DOF) in lieu of scalars. Of
course, the number of eigenvalues (natural frequen-
cies) and eigenvectors (corresponding modal shapes)
recovered is again N.
CSEDU2012-4thInternationalConferenceonComputerSupportedEducation
300
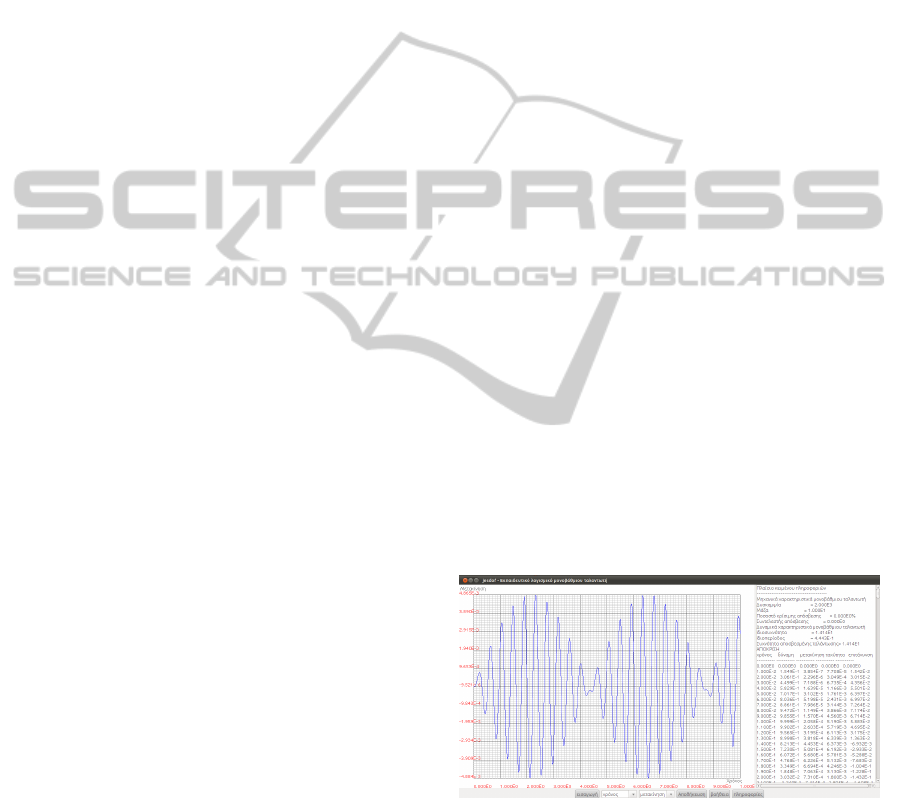
5 1-STORY 3D FRAME “JSISMA”
Module “jsisma” focuses on a single story, 3D build-
ing that comprises an arbitrary number of vertical
stiffness (column) elements, whose position and me-
chanical properties are specified by the user, plus a
heavy floor slab. The column elements may be inex-
tensional or may have zero resistance to torsion. The
floor slab is considered to act as a rigid diaphragm
in the horizontal plane. There are also two options
concerning its out-of-plane rigidity, namely flexible
or rigid. The set of output parameters computed by
this module are stiffness and mass matrices, the co-
ordinates of elastic centre and the inertial radius, the
period, frequency and coordinates of each eigenvec-
tor, and the coordinates of modal poles. The diffi-
culty with space frames is the correct definition of
their stiffness and masses, once the dominant mode
of deformation motion has been defined.
6 PLANAR FRAME “JTFRAME”
Application module “jTframe” examines a three story
plane frame with base isolation which translates into a
four DOF system, whose properties are user defined:
elastic and inertial characteristics plus the geometrical
configuration. This module computes and presents in
simple text area the following fundamental data: stiff-
ness matrix, mass matrix, period and frequency asso-
ciated with each eigenmode, the components for each
eigenvector, plus the participation factor, generalized
mass and effective mass corresponding to each eigen-
mode. Next, there is an option to specify an acceler-
ation response spectrum, in which case the program
proceeds to calculate the spectral response for each
eigenmode. Up to this point, module “jTframe” is
similar to module “jframe”, except for the fact that
the user may define a variable number of stories and
incorporate base isolation. Next, the user may define
time-dependent loads at each story level, either as an-
alytical functions of time or from an external ASCII
file. Also, the transient loading may be given in terms
of a base acceleration file. After specifying the dis-
crete time step and the total time of duration, the tran-
sient response of the frame is computed and results
are presented through use of a GUI application. In
here, the animation option has been utilized and the
frame motion is shown in real time, in parallel with a
conventional plot for time history at a specified point
on the structure. These last plots allow the user to
define parameters for the two axes chosen from the
set of time, displacement, velocity, acceleration, and
external load at each story level.
7 NUMERICAL EXAMPLES
In this section some illustrative examples using mod-
ules of EDUSOFT follow to show the use of educa-
tional packages.
7.1 Computation of SDOF Response
In here, we will use application module “jesdof” to il-
lustrate the use of these web-based educational pack-
ages. More specifically, the input parameters re-
quested by this module are (i) stiffness, mass and
damping ratio of the SDOF system, (ii) initial con-
ditions, (iii) description of the external force (analyt-
ical function of time or from an external ASCII file),
and (iv) integration parameters for Duhamel’s integral
(default values are recommended). Output is (i) nat-
ural period and (ii) graphical representation of the re-
sponse (displacement, velocity, acceleration) as func-
tions of time. For an SDOF system with properties
m = 10 tons, k = 200 kN/m, ζ = 5%
under a unit harmonic load of the type
f(t) = sin(1.1ω
0
t), 0 ≤ t ≤ 10sec
and zero initial conditions, a sample output screen is
given in Figure 1 for the displacement time history.
For the same system with initial conditions
u
0
= 0.001m, v
0
= 0.01m/sec
the computed phase space projection on the
displacement-velocity plane is plotted in Figure 2.
Similar examples can be worked out for various types
of loading functions in combination with the initial
conditions.
Figure 1: Module “jesdof” screen depicting the SDOF dis-
placement time response x(t) (in m) for an external har-
monic loading.
7.2 Transient Response of a Planar
Frame
The structure here is understood to be a simple, fixed
base, single-bay, three-story frame. What is required
EDUSOFTPACKAGEFORSTRUCTURALENGINEERING-Web-basedEducationalMaterialusingJAVAfor
StructuralDynamics
301
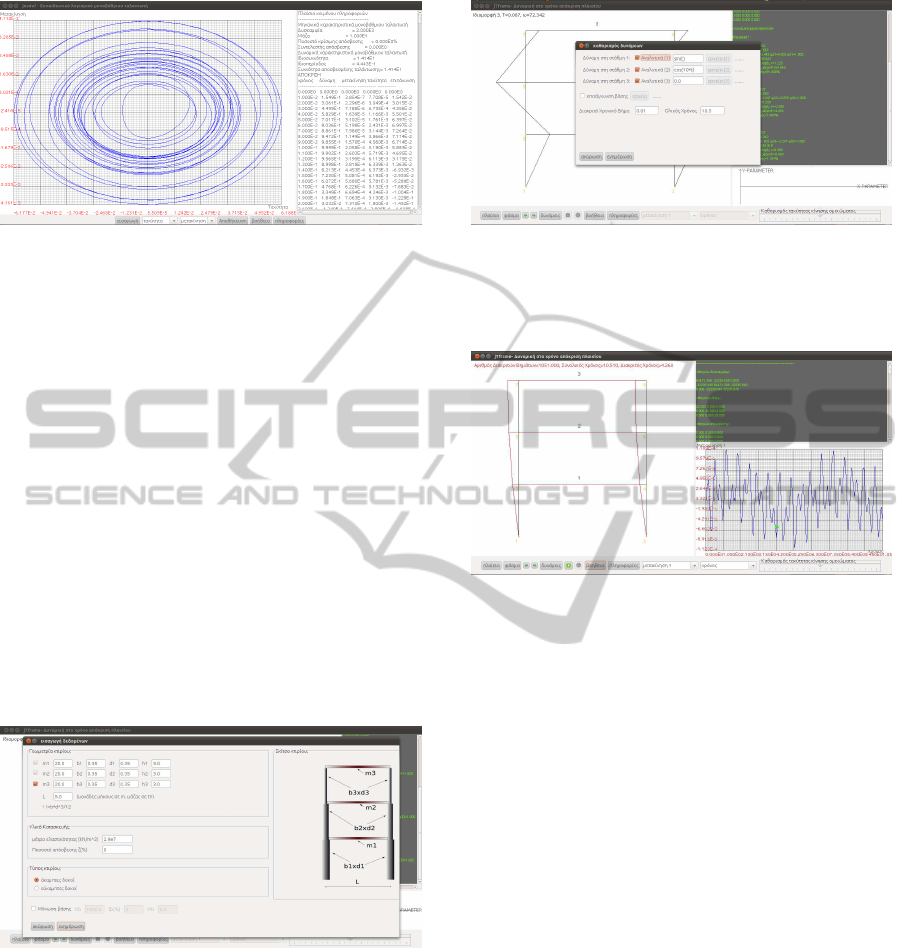
Figure 2: GUI from module “jesdof” depicting an SDOF
computed response to initial conditions as a phase space
projection in terms of displacement versus velocity.
as input is (i) lateral dimension and story heights
(in m), (ii) story masses (in tons), (iii) cross-section
lateral stiffness of the columns (in kN/m) and their
modulus of elasticity (in kN/m
2
) (beams are assumed
rigid), and (iv) the input response spectrum (either
from use of “espec” or from an external ASCII file).
Output comprises (i) graphical representation of the
frame’s modal shapes and associated natural frequen-
cies, (ii) generalized mass values and participation
factors, and (iii) the resulting spectral displacements,
velocities and accelerations for each mode of the
structure. Figure 3 depicts the input dialog for a three-
story frame and in Figure 4 we present the respec-
tive input dialog for the forces. Finally, output re-
garding this example is given in reference to module
“jTframe” in Figure 5 .
Figure 3: Module “jTframe” input dialog box defining
the geometrical and material properties of the three-story
frame.
8 CONCLUSIONS
Regarding actual use of the present educational pack-
age for structural dynamics analysis, we conclude that
the teaching experience accumulated during the first
two years of use in actual classroom environment has
been most positive. Three modulus (“jesdof”, “es-
Figure 4: Module “jTframe” input dialog box defining the
external time-dependent loads, the total time interval of in-
terest plus the time step, followed by output of modal infor-
mation.
Figure 5: Module “jTframe” screen depicting a time history
animation of the three-story frame motion plus its displace-
ment response as defined by the user; the green box marks
current state information.
pec”, “jframe”) were taught to 4th year undergradu-
ates after the first five weeks of instruction, in groups
of 35 students, for a two hour period in a computer
laboratory. These sessions were preceded by lec-
tures summarizing basic structural dynamics concepts
and the relevant material was accessible through the
electronic address http//:blackboard.lib.auth.gr. They
were then followed up by two more lectures on the
semester project, for which the students could utilize
the tools available to help complete it. Course eval-
uation results indicated a favourable reception of this
type of classroom activity by the students involved.
ACKNOWLEDGEMENTS
The EPEAEK II project entitled “Upgrading Civil
Engineering Studies at AUTH”, 2007-2009, is ac-
knowledged.
CSEDU2012-4thInternationalConferenceonComputerSupportedEducation
302

REFERENCES
CEN (2004). Eurocode 8. design provisions of structures for
earthquake resistance. part 1: General rules, seismic
actions and rules for buildings. European Committee
for Standardization, Brussels, Belgium.
Chopra, A. (2007). Dynamics of Structures: Theory and Ap-
plications to Earthquake Engineering. Prentice-Hall,
Upper Saddle River, New Jersey.
Gosling, J., Joy, B., Steele, G., and Bracha, G. (2005). The
Java Language Specification Third Edition. Addison-
Wesley, third edition edition.
Katsanos, E., Taskari, O., and Sextos, A. (2011). A matlab-
based educational tool for seismic design of flexibly
supported r/c buildings. Computer Applications in En-
gineering Education, DOI 10.1002/cae.20568.
Sobhaninejad, G., Hori, M., and Kabeyasawa, T. (2011).
Enhancing integrated earthquake simulation with high
performance computing. Advances in Engineering
Software, 42:286–292.
APPENDIX
In terms of programming, a minimum prerequisite for
a modern educational-type development is use of the
graphical user interface (GUI). Another aspect to be
considered is the “open source” policy for software.
The philosophy behind this type of policy arises nat-
urally in an academic environment, where free shar-
ing of information is crucial for the development and
dissemination of technology in the context of both re-
search and education. Furthermore, we opt to use here
the Java Web Start technology instead of the Java Ap-
plet technology that is common in the majority of ap-
plications.
Finally, we mention here the extensibility of such
applications, in order to be modified in several lan-
guages, using the internationalization feature of Java.
It is also relatively straightforward to include more
advanced topics, as for example non-linear response
in the case of “jframe” or “jTframe”, that would be of
considerable interest in postgraduate study courses in
advanced structural dynamics.
EDUSOFTPACKAGEFORSTRUCTURALENGINEERING-Web-basedEducationalMaterialusingJAVAfor
StructuralDynamics
303
