MULTI-LEVEL GROUPING GENETIC ALGORITHM

FOR LOW CARBON VIRTUAL PRIVATE CLOUDS

Fereydoun Farrahi Moghaddam, Reza Farrahi Moghaddam and Mohamed Cheriet

Synchromedia Laboratory,

Ecole de Technologie Sup

erieure, Montreal, QC, Canada

Keywords:

Cloud Computing, Virtual Private Cloud, Green IT, Carbon Footprint, Genetic Algorithm, Multi-level

Grouping.

Abstract:

Optimization problem of physical servers consolidation is very important for energy efﬁciency and cost reduc-

tion of data centers. For this type of problems, which can be considered as bin-packing problems, traditional

heuristic algorithms such as Genetic Algorithm (GA) are not suitable. Therefore, other heuristic algorithms are

proposed instead, such as Grouping Genetic Algorithm (GGA), which are able to preserve the group features

of the problem. Although GGA have achieved good results on server consolidation in a given data center, they

are weak in optimization of a network of data centers. In this paper, a new grouping genetic algorithm is in-

troduced which is called Multi-Level Grouping Genetic Algorithm (MLGGA), and is designed for multi-level

bin packing problems such as optimization of a network of data centers for carbon footprint reduction, energy

efﬁciency, and operation cost reduction. The new MLGGA algorithm is tested on a real world problem in a

simulation platform, and its results are compared with the GGA results. The comparison shows a signiﬁcant

increase in the performance achieved by the proposed MLGGA algorithm.

1 INTRODUCTION

Global warming and its impacts on our life is one of

the biggest twenty-ﬁrst century’s challenges for hu-

man societies. There are different reasons for global

warming, but one of main reasons is known to be ex-

cessive Green House Gases (GHG) emissions. Nowa-

days, the share of ICT sector in the total GHG emis-

sions is not greater than 2% (McKinsey, 2007). How-

ever, according to rapid growth of ICT sector within

the ICT enabling effect (Webb, 2008), in near future,

GHG emission reduction in ICT sector will be very

important.

After introduction of virtualization technology,

physical server consolidation plays an important role

in energy efﬁciency and GHG emission reduction in

data centers (Beloglazov et al., 2010)(Gmach et al.,

2009)(Liu et al., 2009). In this type of problems, the

objective is fulﬁlled by minimizing the energy con-

sumption, carbon footprint, cost, or a mixture of them.

Considering the locations of VMs as variables of the

problem and one of the aforementioned cost func-

tions, the consolidation problem can be written as a

bin-packing optimization problem. Bin packing algo-

rithms such as improved First Fit Decreasing (FFD)

and Least Loaded (LL) (Ajiro and Tanaka, 2007) as

well as heuristic optimization algorithms can be used

in order to solve this type of problems.

Because of high complexity of this kind of op-

timization problems, heuristic algorithms are good

candidates for them. But traditional general heuris-

tic algorithms such as GA are not able to provide a

good solution for the special case of server consoli-

dation (Xu and Fortes, 2010). Particular genetic op-

erators which take advantage of the group-oriented

structure of cost function, could lead the genetic al-

gorithm to better results compare to the non-grouping

heuristic algorithms which are not aware of that struc-

ture. For example, the GGA has been used to achieve

more efﬁcient results in various works (Xu and Fortes,

2010)(Agrawal et al., 2009)(Wilcox et al., 2011).

These new methods are proven to have better results

than traditional methods and global heuristic algo-

rithms.

Ability to migrate virtual machines in a lively

manner from one data center to another data

center without service interruption (Clark et al.,

2005)(Van der Merwe et al., 2010)(Wood et al.,

2010)(Wood et al., 2009)(Farrahi Moghaddam and

Cheriet, 2010), opens the door to more complex archi-

tectures and behaviors of connected data centers and

brings higher opportunity for GHG, and mainly car-

315

Farrahi Moghaddam F., Farrahi Moghaddam R. and Cheriet M..

MULTI-LEVEL GROUPING GENETIC ALGORITHM FOR LOW CARBON VIRTUAL PRIVATE CLOUDS.

DOI: 10.5220/0003903303150324

In Proceedings of the 2nd International Conference on Cloud Computing and Services Science (CLOSER-2012), pages 315-324

ISBN: 978-989-8565-05-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

bon footprint reduction (Farrahi Moghaddam et al.,

2011). Higher complexity of new designs requires

better and more efﬁcient optimization algorithm in or-

der to reduce the GHG emissions as much as possible

in real-time in response to the unpredicted variations

in the workload and energy sources. In these net-

works, not only server consolidation should be con-

sidered, but also for each VM the best data center

should be chosen while meeting all the constrains.

In this type of complex problems, even algorithms

such as the GGA, are not able to discover all the re-

lations between VMs, servers and data centers to lead

to the best optimal solution. As a bin-packing algo-

rithm, GGA is able to beneﬁt from consolidation of

VMs on servers, while it cannot discover the possible

beneﬁts of data center consolidation. Therefore, even

a more complex heuristic algorithm is needed in order

to discover these relations and behaviors.

In this paper, a new genetic algorithm is proposed

as multi-level grouping genetic algorithm (MLGGA),

and we argue that this algorithm is useful for those

types of problems which deal with different levels of

bin packing. This new algorithm will consider not

only the relation of individuals as groups, it also con-

siders the relation of groups of groups in order to

achieve the best possible solution for the optimization

problem. As a use case in this work, a network of data

centers is optimized for carbon footprint reduction. it

is worth noting that the concept of the MLGGA could

be used in any optimization problem which deals with

groups of groups in different levels and their relations.

The paper is organized as follows. In the ﬁrst

section, different works on using heuristic algorithms

for server consolidation, energy efﬁciency and carbon

footprint reduction are reviewed. In the next section,

the principle of the proposed algorithm is explained.

In the next section, a case study is planned for com-

parison of the proposed algorithm with GGA. Finally,

in the last section, the conclusion and some prospects

for future works are discussed.

2 RELATED WORKS

2.1 Grouping Genetic Algorithm

In (Falkenauer and Delchambre, 1992), Falkenauer

and Delchambre proposed a new version of genetic al-

gorithm known as grouping genetic algorithm. They

argue that normal genetic crossover and mutation op-

erators are not able to preserve the group features of

the parent chromosomes. In the straightforward en-

coding scheme, each item (for example, a VM) is rep-

resented by a gene in the chromosome, and its label is

its group (for example, a server) which that item be-

longs to. For example, the chromosome ADEBFFBC

encode a solution for 8 VMs where the ﬁrst VM is

on server A, the second VM is on server D, and so

on. Basically, when there are two parents with good

groups deﬁned in their chromosomes, there is no way

for normal genetic crossover operator to create an

offspring in which those good groups are preserved.

A part of a child chromosome comes from one par-

ent, and the rest comes from the other parent, well-

deﬁned groups in both parents will break in parts, and

the probability of having an offspring with stronger

groups is very low. Therefore, they proposed a new

crossover and mutation operators in their new algo-

rithm, which perform on groups instead of individual

genes.

In their crossover operator, the groups presented

in the chromosomes are lined up (keeping one gene

per group), and the crossover will happen on these

two group representations of the parents. For ex-

ample, for the chromosome ADEBFFBC, the group

lineup will be ADEBFC. It is worth noting that, in

the group representation the chromosomes could be

of variable length. Two crossover points will be se-

lected in each parent group-lineup randomly. And,

the groups in middle part of the second parent group-

lineup will be inserted in ﬁrst parent group-lineup at

the ﬁrst crossover point. For example, the group-

lineup of the parents are as follows:

P1 : ADE|BF|C (ADEBFFBC)

P2 : bd|ca| (bbdcabba)

where the groups with same alphabetic character but

with different cases (upper and lower cases) are same

but represent that group in ﬁrst and second parent, and

crossover points are marked as |. Also, the straight-

forward encoding of the chromosome is provided in

parentheses.

After insertion, the offspring group lineup of the

offspring will look like (ADEcaBFC). Because the

groups “c” and “a” are inserted from the second par-

ent, their matched groups in ﬁrst parent “C” and “A”,

are no longer valid and these two groups and all their

assignments to individual genes will be removed from

the offspring; remaining the offspring group lineup as

(DEcaBF). For our example, the straightforward en-

coding of the offspring will be: (?DEcaFBa). ”?”

symbol shows that the ﬁrst individual gene has no

group assigned to it any more because group A is re-

moved from the chromosome. In a same way, there

are some individuals which are in groups “c” and “a”

in second parent while they are in other groups in

ﬁrst parent. The group of these individuals will be

replaced with inserting groups from second chromo-

some. The groups of replaced individuals need to

CLOSER2012-2ndInternationalConferenceonCloudComputingandServicesScience

316

be removed with all assignment to individual genes

which are groups “B” and “F” in the ﬁrst parent. For

our example, the straightforward encoding of the off-

spring will be: (?DEca??a). Now, there are some in-

dividuals which their group assignments are removed

from chromosome in previous actions which needs

to be reinserted in the offspring chromosome. First

Fit Descending algorithm (Garey and Johnson, 1979)

is used in order to reinsert the removed individuals

into the chromosome. The priority is with the groups

which are almost full.

In mutation operator of grouping genetic algo-

rithm, the lineup of groups will be created in a similar

way of the crossover operation. Then, some groups

will be chosen by random and those groups with their

containing individuals will be removed from the chro-

mosome. Then, there are some individuals, which

have been removed in previous action, and are needed

to be reinserted into the chromosome. A similar ac-

tion as that of the crossover operator will be taken

here in order to reinsert the removed individuals into

the chromosome.

2.2 GGA in Server Consolidation

Xu et al. used Grouping Genetic Algorithm (GGA)

in (Xu and Fortes, 2010) in order to achieve multi-

objective goals in placement of virtual machines in

virtualized data center environments. They claimed

that normal GGA crossover operator is not efﬁcient

and they modiﬁed it to achieve better results. They

proposed a ranking-crossover instead, and claimed

that new crossover is able to inherit good features

from parents more efﬁciently. They evaluated all the

individuals based on three evaluation functions which

they used to represent their three optimization objec-

tives. These three objectives were resource usage ef-

ﬁciency, power consumption efﬁciency, and thermal

efﬁciency. They represented some evaluation func-

tions for each of these objectives. The evaluation re-

sults were some numbers in the range of [0,1]. Instead

of random selection of crossover points, the selected

groups for insertion to the ﬁrst chromosome are most

likely selected from groups with higher rank in rank-

ing evaluation of three objectives. They claimed that

this way, the high quality groups will most probably

remain intact and optimizer will reach to better so-

lutions faster. They also combined GGA with fuzzy

concepts in order to achieve the best solution for their

several objectives problem.

Shubham Agrawal et al. used the GGA algorithm

for a server consolidation problem in (Agrawal et al.,

2009). They modeled the server consolidation prob-

lem as a vector packing problem with conﬂicts. In

their mathematical model, they tried to differentiate

between efﬁciency of bin packing and number of bins

which are packed. Their model was designed to prefer

the bin-packing efﬁciency over bin number optimiza-

tion. They used the original version of the GGA in

order to solve the optimization problem.

In another work, David Wilcox et al. introduced

another type of GGA algorithm known as Reorder-

ing Grouping Genetic Algorithm (RGGA) (Wilcox

et al., 2011). They describe the multi-capacity bin-

packing problem in data center server consolidation

as bins (servers) with multiple capacities (CPU, mem-

ory, network, storage, and etc.) and VMs with mul-

tiple weights. In their proposed grouping genetic al-

gorithm, each individual has several representations,

and they claim these multiple representation will lead

to better solution in more efﬁcient time frame. Parent

chromosomes are chosen with a higher probability for

more ﬁt individuals. In their approach, they combined

all the bins from both parent chromosomes and sort

them by ﬁtness. The fuller a bin is, it is on top of

the list, and less full bins are at the bottom of the list.

From the top of the list, some bins will be selected

and the rest of the bins will be discarded. If there is a

bin which contain an individual belongs to already se-

lected bins, that bin will be discarded as well. For the

individuals which are discarded, they will be ordered

by their ﬁtness and ﬁrst ﬁt descending algorithm will

be used in order to reinsert them to the offspring chro-

mosome.

Because the algorithm always prefers tightly

packed bins over other bins, they added a Gaussian

noise to the ﬁtness function of the individuals in order

to escape the local minimums. Respectively, in their

mutation operator, the mutation take place more on

less ﬁt bins than good bins. This will assure that the

structure of good groups does not intact often. They

used three mutation operator. First, normal GGA mu-

tation while some bins will remove randomly and

their individuals will reinsert into the chromosome.

Second, two items in the order list will be swapped,

and third, one item will be randomly relocate in the

order list.

3 MULTI-LEVEL GROUPING

GENETIC ALGORITHM

In the GGA, a new crossover and mutation operators

were introduced in order to save the group relations

between individual genes. In a similar way, here, the

MLGGA crossover and MLGGA mutation operators

are introduced in order to preserve the relations be-

tween groups. These operators substitute the normal

MULTI-LEVELGROUPINGGENETICALGORITHMFORLOWCARBONVIRTUALPRIVATECLOUDS

317

GA crossover and mutation operators and work along

with the other GA operators as shown in lines 6 and 7

of the following MLGGA pseudocode:

1: Choose initial population.

2: Evaluate each individual’s fitness.

3: repeat

4: Select individuals to reproduce.

5: Mate pairs at random.

6: Apply MLGGA crossover operator.

7: Apply MLGGA mutation operator.

8: Evaluate each individual’s fitness.

9: until terminating condition

3.1 MLGGA Crossover

In the virtual cloud problems, the positions of VMs

are the variables of the problem. In these problems,

grouped variables, such as server consolidation, lower

the cost function. However, normal GA crossover

break the existing groups in parent genes, and prob-

ability of preserving the good grouping features pre-

sented in parent genes is very low. Although the GGA

crossover provides a way to preserve the grouping

features in parent genes, there are relations between

groups that the GGA crossover is not able to preserve,

and most probably it breaks these relations. In the net-

work of data centers, the GGA is good to consolidate

VMs on servers, but it is not able to identify that there

are beneﬁts in choosing servers from only one data

center. For example, the GGA may consolidate VMs

on different servers which allow us to turn off some of

the servers and save energy, but it is not aware that if

it consolidate all servers on less number of data cen-

ters as well, it may save a lot more by turning off an

intermittent data center.

For example, assuming parent genes P1 and P2

and their groups are as follow:

P1 : ACDEGIJB

(ACDEGAIJDCBACDEAGIA)

P2 : bcghieda

(bcghieddaccccehigha)

If each group is assigned to a higher level group (a

bigger bin) as follows:

W={A} X={B,C}, Y={D,E,F}, Z={G,H,I,J}

w={a} x={b,c}, y={d,e,f}, z={g,h,i,j}

The genes group lineup can be rewritten as their

higher level groups as follows by replacing the group

representations (for example, ACDEGIJB for P1) by

their higher level group labels:

P1 : WXYYZZZX ← ACDEGIJB

P2 : xxzzzyyw ← bcghieda

As it is shown above, some higher level groups

are repeated in the group lineup. Here, we create a

higher level group lineup (level 2 group lineup), and

we keep only one gene per higher level group similar

to what we did in group lineup in lower level. Now,

the chromosome could be written as below:

P1 : WXYZ WXYYZZZX

(ACDEGAIJDCBACDEAGIA)

P2 : xzyw xxzzzyyw

(bcghieddaccccehigha)

where the ﬁrst column is the new level 2 group

lineup representation of the chromosomes. The

crossover will be done on the level 2 group lineup rep-

resentation of the genes: (WXYZ) and (xzyw). Like

the GGA, two crossover point will be chosen ran-

domly on each gene:

P1 : WX|Y|Z WXYYZZZX

(ACDEGAIJDCBACDEAGIA)

P2 : x|zy|w xxzzzyyw

(bcghieddaccccehigha)

and the middle part of second gene will be inserted

to the ﬁrst gene, and similar higher level groups in

ﬁrst gene with their assigned groups and containing

individuals will be removed from the gene.

Offspring : WX|zyY|Z

As it is shown in above, higher level groups (z) and

(y) are inserted from second parent to the ﬁrst parent.

This means that their matching higher level groups

(Z) and (Y) are not any more valid and their contain-

ing groups (D,E,F,G,H,I,J) and their containing in-

dividuals should be removed from the chromosome;

which remains the offspring chromosome as below:

Offspring : WXzy (ACghiedd?CBACehighA)

Genes number 3-8, and 14-18 in second parent (P2)

are belongs to groups (d,e,f,g,h,i,j) which are belongs

to higher groups (y,z) and they are transferred directly

from second chromosome to the ﬁrst chromosome.

Gene number 9 is in group (D) in ﬁrst parent which

belongs to higher level group (Y) which needs to be

removed as mentioned above.

For the genes in ﬁrst parent, which are replaced

with genes from second parents, there are some indi-

viduals which are belongs to some groups and higher

level groups which are not yet removed from the chro-

mosome. For our example, genes number 6 and 16 are

belong to group (A) in ﬁrst parent chromosome which

are replaced with (e) and (i) from the second parent

chromosome. These individuals with their co-group

and co-higher-group individuals need to be removed

from the chromosome as well. Co-group individuals

of an individual are those genes which are in the same

group, and co-higher-group individuals of and indi-

vidual are those genes which are in the same higher

CLOSER2012-2ndInternationalConferenceonCloudComputingandServicesScience

318

group. For our example, all individuals in higher level

group (W) which is higher level group of (A) need to

be removed from the offspring chromosome. For our

example, the offspring chromosome will be like this:

Offspring : Xzy (?Cghiedd?CB?Cehigh?)

As it is shown in above, higher level groups (X) from

ﬁrst parent, and (z) and (y) from the second parent are

preserved in the offspring chromosome intact which

is the goal of the crossover operator.

At the end, there are some individuals which are

not assigned to any group and higher level group.

These individuals will ﬁt in the chromosome by us-

ing the First Fit Descending algorithm or more ad-

vanced ﬁtting techniques. Higher level groups which

are fuller will chosen ﬁrst, and also fuller groups are

in more priority for ﬁrst ﬁt algorithm.

3.2 MLGGA Mutation

The MLGGA mutation is very similar to the MLGGA

crossover concept. From a selected chromosome:

P1 : WXYZ WXYYZZZX

(ACDEGAIJDCBACDEAGIA)

Some higher level groups will be randomly cho-

sen, and all co-group and co-higher-group individual

genes will be removed from the chromosome. For our

example, if higher level group (Z) is selected to be re-

moved, the remaining chromosome will be as below:

P1 : WXY WXYY???X

(ACDE?A??DCBACDEA??A)

Then, the First Fit algorithm will be used to reinsert

them to the chromosome as described in crossover op-

erator section.

3.3 Extensions of the MLGGA

Crossover and Mutation

In the GGA, the concept of group of individual genes

is introduced. In previous section, we described a sit-

uation where there are some relations between groups

of groups in a problem. We can extend this solution

for cases in which there are several level of group-

ing involved. For example, if, in a problem, individ-

uals are grouped by some criteria, the problem has

grouping relations at level 1. If the groups of level

1 are grouped by some other criteria, there will then

be a grouping of level 2. And similarly, we can have

grouping of level n for a problem.

For a problem with the grouping of level n, a level

n MLGGA crossover and mutation should be used.

The concept of the level-n MLGGA crossover and

mutation is similar to what we described in previous

subsections which was a level-2 MLGGA crossover

and mutation. For the level-n MLGGA crossover, in-

dividual genes will be represent by their level 1, level

2, ..., level n groups. Two crossover point will be se-

lected randomly in parents level-n groups representa-

tion, and the second part of second chromosome will

be inserted to the ﬁrst chromosome. The matching

level-n groups in ﬁrst chromosome with all their indi-

viduals will be removed from the offspring chromo-

some. For those individual genes in ﬁrst parent which

are replaced with transferring genes from second par-

ent, all their co-level-n-group individual genes will be

removed as well. Co-level-n-group individuals of an

individual are those genes which are in the same level

n group. At the end, all removed individuals will be

inserted to the chromosome with using an First Fit al-

gorithm or more advanced algorithms as described in

previous subsections. According to this deﬁnition, the

GGA algorithm is a level-1 MLGGA.

Level-n mutation operator will be deﬁned in a

very similar way with randomly selecting some level-

n groups and removing their individuals and reinsert-

ing them.

4 VIRTUAL PRIVATE CLOUD

USE CASE

In order to examine the performance of new algorithm

on energy efﬁciency and Carbon footprint reduction,

we test it in a simulation platform. A Virtual Pri-

vate Cloud (VPC) (Van der Merwe et al., 2010)(Wood

et al., 2010)(Farrahi Moghaddam et al., 2011) is sim-

ulated and tested under two heuristic algorithms: the

GGA and the proposed MLGGA. Different case stud-

ies are considered to test the proposed algorithm as

follows:

• Medium-scale network under normal load (Case

study 1):

In this case study, a network of 7 data centers in

7 cities around the world is simulated and car-

bon footprint and energy consumption of the net-

work is measured under different optimization al-

gorithms. Initial utilization of servers are about

60% in this case study. This case study shows

how the proposed algorithm competes with the

other algorithm in a medium-scale network under

medium utilization. This case study is the base-

line case study for this research. Some parameters

is changed in this case study to create new case

studies. For example, in order to see the effect of

high utilization on the algorithms, the following

case study is considered.

MULTI-LEVELGROUPINGGENETICALGORITHMFORLOWCARBONVIRTUALPRIVATECLOUDS

319

• Medium-scale network under heavy load (Case

study 2):

In this case study, A network similar to case study

1 is simulated and Carbon footprint and energy

consumption of the network is measured under

different optimization algorithms. Initial utiliza-

tion of servers are about 90%. This case study

shows how the proposed algorithm outperforms

the other algorithm in a medium-scale network

under heavy utilization.

Another important parameter is the network size

which is considered in the following case study

in which a large-scale network is deﬁned in order

to show the effect of the size of network on the

algorithms.

• Large-scale network under normal load (Case

study 3):

In this case study, A network of 20 data centers in

11 cities are simulated and carbon footprint and

energy consumption of the network is measured

under different optimization algorithms. Initial

utilization of servers are the same as case study 1.

This case study compares the performance of the

new algorithm compete with other algorithm in a

Large-scale network under medium utilization.

4.1 Simulation Platform Speciﬁcations

Simulation platform is designed in Matlab environ-

ment. In this platform, a set of components are sim-

ulated such as data centers, servers, VMs, VM mi-

grations, and weather conditions. It is possible to de-

ﬁne more than one data centers in each selected cities

in this simulation platform. Each data center can be

connected to a source of renewable energy and alter-

native non-green source of energy. Renewable source

of energies which are simulated in this environment

includes solar, wind, hydro, and nuclear source of en-

ergies. There is battery bank in each data center which

stores extra green power to be used when the source of

green energy is not available. The simulator estimates

the energy used in each data center based on the num-

ber of running servers and other utilities, and calcu-

lates the extra green power. Knowing the extra green

power at a moment, the simulator will update the bat-

tery charge of each data center. Not all source of green

power are the same, and each renewable source of

energy has its own cleanness measured as the g fac-

tor (Farrahi Moghaddam et al., 2011). The g factor

changes according to the availability of source of en-

ergy and charge of batteries in each node. For exam-

ple, for solar and wind energy, if there is enough en-

ergy stored in the batteries, the g is high. In contrast,

when the batteries are discharged and data center is

using the grid energy the g factor is low. For hydro

and nuclear energy, if energy exist, g factor is always

high, and for grid energy powered by coal, g factor is

always low.

4.2 Optimization Algorithms

To evaluate the efﬁciency of the proposed algorithm,

the MLGGA algorithm is compared with the GGA

algorithm which is used in other works for energy ef-

ﬁciency in virtualized data center environments. car-

bon footprint and energy consumption of the network

are also measured when there is no optimization in

order to have a baseline in the comparison of the re-

sults of the GGA and the MLGGA. This will show

how much energy and carbon these two algorithm can

save. As shown in the previous works section, there

are things which can be done to improve the result

of the GGA in energy efﬁciency in virtualized data

center environment. Here, we use the same improve-

ments for both GGA and MLGGA as described in

previous works. The only differences between the two

algorithms implementation are the crossover and mu-

tation operators, and the rest of the algorithms are ex-

actly the same, and both algorithms beneﬁt from the

enhancements.

4.3 Carbon and Energy Measurement

One of very important parts of the new algorithm eval-

uation is the carbon and energy measures which are

used to show the carbon/energy footprint of the whole

network. For this research, a measurement tool which

is developed for virtual private clouds is used to mea-

sure the Carbon and energy footprint of the whole net-

work of data centers (Kansal et al., 2010)(Economou

et al., 2006)(Farrahi Moghaddam et al., 2011). For

Carbon footprint the following formulation is used:

C(t,∆

) = C

(∆

) +C

on/o f f

(∆

)

+ρ

max

∑

(1 − g

(t))



(t)+ P

(t)

∑

s∈d

(α

cpu

+α

mem

+α

disk

+ γ

)



∆

(1)

where C(t,∆

) is the total carbon footprint of the net-

work in time t for time period of ∆

. For more details

please see (Farrahi Moghaddam et al., 2011).

And for energy measurement, the following for-

mulation is used:

E(t,∆

) = C

(∆

)/ρ

max

on/o f f

(∆

)/ρ

max

∑



(t)+ P

(t)

∑

s∈d

(α

cpu

+α

mem

+α

disk

+ γ

)



∆

(2)

CLOSER2012-2ndInternationalConferenceonCloudComputingandServicesScience

320

where E(t,∆

) is the total energy consumption of the

network in time t for time period of ∆

. For more

details please see (Farrahi Moghaddam et al., 2011).

The objective of this work is to reduce the car-

bon footprint and emissions. As shown in (Farrahi

Moghaddam et al., 2011), Carbon optimization and

energy optimization are not equivalent in VPC envi-

ronments. When the Carbon is optimized, energy is

not necessary optimized. Here, the energy is mea-

sured just as a reference, and no optimization with re-

spect to energy is performed. There are many works

that deal with energy efﬁciency in the literature such

as dynamic CPU speed, energy-aware job scheduling,

server consolidation (Zhang et al., 2008).

4.4 Results

The algorithms are tested on medium-scale and large-

scale networks in a simulation environment

which

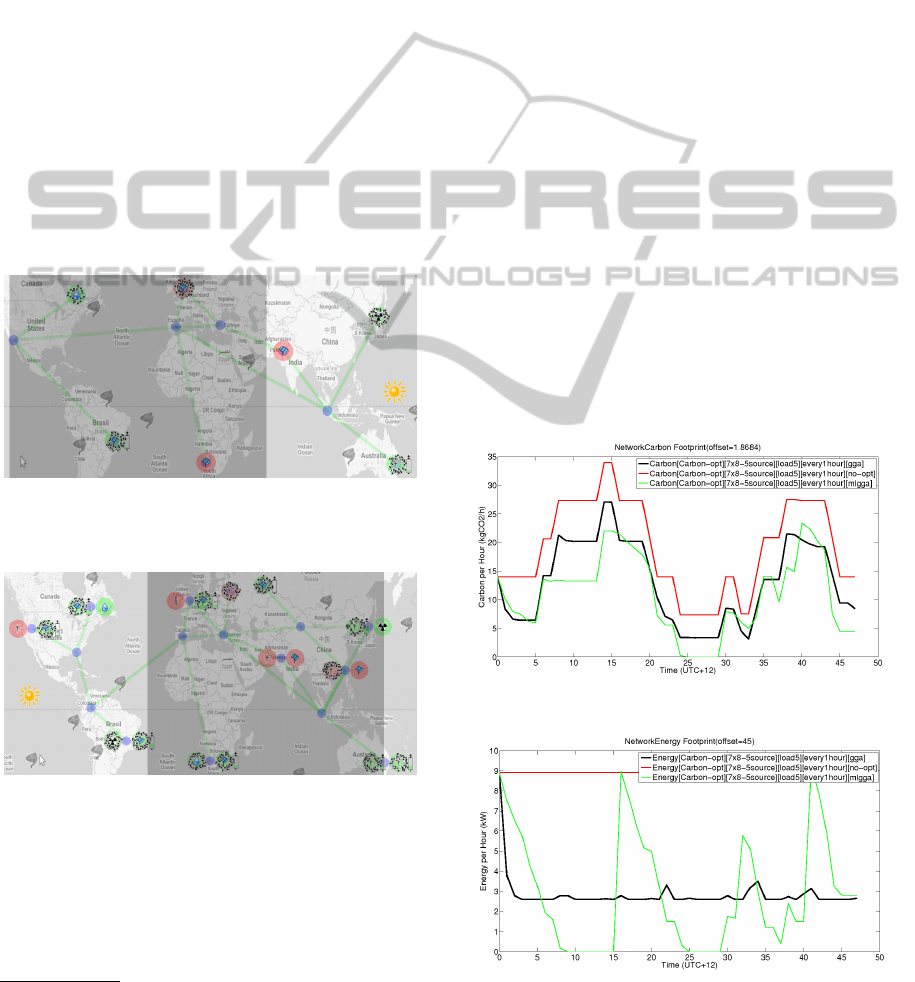
are shown in Figure 1 and Figure 2.

Figure 1: Medium-scale network of data centers (case study

1).

Figure 2: Large-scale network of data centers (case study

3).

As it is depicted in Figures 1 and 2, each data cen-

ter is illustrated with a red or green ﬁlled circle. Red

circle means that data center is using a source of en-

ergy with a g factor less than 0.5, and green circle

means that data center is using a source of energy with

http://www.greenservices.info/2011/10/simulation-

environment.html

g factor greater than 0.5. The type of source of energy

for each data center is illustrated as an icon in the mid-

dle of the circle. Available source of energies in this

simulation are solar, wind, hydro, nuclear, and grid

(coal). As it is shown, hydro and nuclear source of

energies are always green, and grid source of energy

is always red. For solar and wind source of energies,

it depends on existence of sun and wind, and also on

the amount of energy stored in the batteries. For ex-

ample, in Figure 1, the solar power in Brazil is green

even though at the moment the snapshot taken it is

midnight there. It is because of available solar power

stored in batteries of the data center. As it is shown,

there is a battery indicator near the data center which

is reﬂecting the remaining battery charge in each data

center. The battery indicator for data center in Brazil

shows that there is not much battery left and the data

center will soon switch to grid which is a non-green

source of energy. This has already happened for the

data center in South Africa and France. The data cen-

ter in India is in day time, but it is still red. There

are two reason for that. First, it is early morning in

India, so the sun light is not direct, and solar power

generation is low. Second, there is not enough energy

stored in data center batteries in order to enable the

data center to switch from grid power to solar power.

For case study 1, measured carbon and energy are

shown in Figures 3 and 4.

Figure 3: Carbon measurement in case study 1.

Figure 4: Energy measurement in case study 1.

MULTI-LEVELGROUPINGGENETICALGORITHMFORLOWCARBONVIRTUALPRIVATECLOUDS

321

In the legend of ﬁgures Figures 3 and 4, Carbon

means that carbon is measured and Energy means that

energy is measures, while [Carbon-opt] means that

for all cases the optimizer was trying to minimize the

carbon and not the consumed energy. The tag [7x8-

5source] shows the structure of the network which is

a 7 data center with 8 server on each data center with

5 different type of source of energy. [every1hour]

means that the optimizations are done for every one

hour, according to (Farrahi Moghaddam et al., 2011)

this is an acceptable interval. [gga], [no-opt], and

[mlgga] represent the optimization algorithm for each

graph. All the graphs need to be summed with the off-

set value in the title of each graph in order to achieve

the real carbon or energy value.

As it is shown in Figure 3, the proposed algorithm

has a better performance compare to the GGA. The

associated curve of the MLGGA is under the curve of

the GGA in the most of time. This is not the case for

the energy as it is shown in Figure 4, and the energy

footprint of the MLGGA is not visually better than

the GGA. As described in (Farrahi Moghaddam et al.,

2011), carbon optimization and energy optimization

are not equivalent in network of data centers with dif-

ferent energy and carbon footprint proﬁles, and here

we conﬁrmed it again.

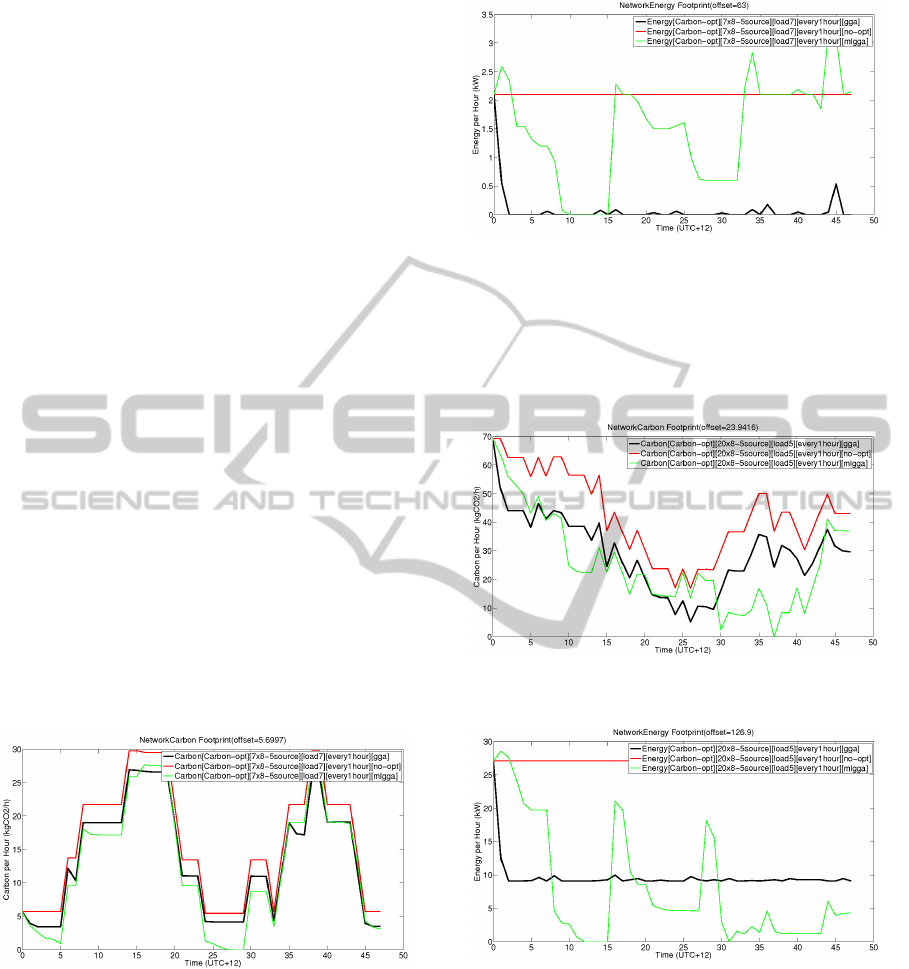
For case study 2, the measured carbon and en-

ergy are shown in Figures 5 and 6. As it is shown,

the MLGGA has a better performance compare to the

GGA, but the difference in the performance is de-

creased because of higher data center utilization.

Figure 5: Carbon measurement in case study 2.

For case study 3, measured carbon and energy are

shown in Figures 7 and 8. The graph shows more

complexity compared to case study 1 and 2 according

to higher number of involved data centers in this case

study. The better performance of the MLGGA is vi-

sually recognizable on the carbon graph. Because the

optimization for each point is not isolated from previ-

ous points, we cannot compare the two curves point

to point. To have a better understanding of the amount

of carbon footprint and energy consumption, the ac-

Figure 6: Energy measurement in case study 2.

cumulated amount of emitted carbon is summarized

in Table 1 and Table 2, and accumulated amount of

consumed energy is summarized in Table 3 and Table

Figure 7: Carbon measurement in case study 3.

Figure 8: Energy measurement in case study 3.

The ”No-opt”, ”GGA”, and ”MLGGA” columns

show the exact measured emitted carbon of the net-

work. the ”GGA %” and ”MLGGA %” columns show

the emissions percentage of the two optimization al-

gorithms with respect to the no-optimization situa-

tion. And the ”MLGGA perf. %” column show the

performance of ”MLGGA” over ”GGA”. As shown

in the Table 1 and Table 2, the MLGGA has a better

performance of 10.65 % over the GGA in case study

1. The MLGGA has better performance compare to

CLOSER2012-2ndInternationalConferenceonCloudComputingandServicesScience

322

Table 1: 48 hour carbon footprint.

Case No-opt GGA MLGGA

study

CO2kg CO2kg CO2kg

Case 1 1009.56 719.79 612.30

Case 2 1040.31 922.92 877.14

Case 3 3202.28 2560.70 2369.49

Table 2: 48 hour carbon footprint.

Case GGA MLGGA MLGGA

study perf.

% % %

Case 1 71.30 60.65 10.65

Case 2 88.72 84.32 4.40

Case 3 79.96 73.99 5.97

the GGA in case study 2 and 3 too, but the better per-

formance is decreased when network is more utilized

or the network is bigger. Overall, the table shows a

better performance for the proposed algorithm. For

more utilized network, it is much harder for the GGA

and the MLGGA to group all the VMs on some data

centers with green energy and empty the one with non

renewable energy due to high number of VMs in the

network.

Table 3: 48 hour energy footprint.

Case No-opt GGA MLGGA

study

KWh KWh KWh

Case 1 2587.20 2296.48 2299.63

Case 2 3124.80 3027.88 3095.52

Case 3 7392.00 6555.61 6466.39

As mentioned earlier, the gain on energy is little

or even negative as it is shown in Table 3 and Table

4. With targeting on Carbon, this loss will pay off in

future with Carbon penalty/reward regulations.

5 CONCLUSIONS AND FUTURE

WORK

According to the results, the level-2 MLGGA, intro-

duced in this work, can provide better results in prob-

lems such as VPC carbon optimization. The GGA

was able to reduce 28.7% carbon emission compare

to no-optimization situation, while the MLGGA was

able to reduce 39.35% carbon emission compare to

no-optimization case which shows that the MLGGA

has an overall 10.65% better performance compared

to the GGA. When the utilization of the network of

data centers is increased, the MLGGA was able to re-

duce 4.4% more in carbon emission compared to the

Table 4: 48 hour energy footprint.

Case GGA MLGGA MLGGA

study perf.

% % %

Case 1 88.76 88.88 -0.12

Case 2 96.90 99.06 -2.16

Case 3 88.69 87.48 1.21

GGA. The decrease in the relative performance com-

pared to the low-utilization case is because of higher

number of VMs in the network. This lowers the pos-

sibility of emptying a whole data center from virtual

machines. But, overall the MLGGA has a better per-

formance in higher utilization compare to the GGA.

In another test, when the network size increased from

7 data centers to 20 data centers with the same rate of

utilization, again the MLGGA outperforms the GGA

with 5.97% extra Carbon emission decrease. Over-

all, the MLGGA has a better performance compared

to the GGA in problems such as low-carbon virtual

private cloud problem.

Beside the carbon footprint, the energy consump-

tion of the network was measured. According to the

results the energy consumption for the MLGGA has

a little improvement or declination compared to the

GGA over time. This is because of the nature of the

virtual private cloud problem. In VPC, which is dis-

tributed over different locations and powered with dif-

ferent source of energies, the carbon footprint reduc-

tion and energy efﬁciency are not equivalent. Accord-

ing to our objective, the carbon footprint was min-

imized. According to the cost of renewable source

of energies, carbon footprint optimization is costly

now, but with implementation of the expected carbon

penalty/reward regulations in the near future, carbon

footprint optimization could be used to minimize the

overall cost of the network as well.

For future works, the following suggestion might

be considered: i) The MLGGA can be used on other

type of grouping problems and success of the al-

gorithm can be compared with other heuristic algo-

rithms, ii) The higher levels of MLGGA can be tested

on problems with higher level of grouping, iii) More

real world data can be used in the simulations in or-

der to make the results more usable in real world VPC

implementations, iv) the energy consumption can be

chosen as target and the indirect carbon footprint re-

duction can be studied, and v) for having a good es-

timation of cost in such a networks, the real cost of

operating a virtual private network can be model and

measured. The measured cost can be compared for

different inter- and intra-data center topologies with

their constraints, such as pooling limits. The solution

will be different for different load scenarios, and also

for different application types running on the VMs.

MULTI-LEVELGROUPINGGENETICALGORITHMFORLOWCARBONVIRTUALPRIVATECLOUDS

323

One scenario could be the comparison of costs of car-

bon footprint optimization and energy consumption

optimization. In additional, various penalty/reward

regulations for carbon footprint reduction, such as

carbon tax, can be model and simulated in order to es-

timate the success rate of such networks in real world

conditions.

ACKNOWLEDGEMENTS

The authors thank CANARIE (Canadian Network for

Advanced Research in Education) for their ﬁnancial

support of the GreenStar Network project. The au-

thors also thank the MDEIE (Ministry of Economic

Development, Innovation and Export Trade) of Que-

bec for their ﬁnancial support.

REFERENCES

Agrawal, S., Bose, S. K., and Sundarrajan, S. (2009).

Grouping Genetic Algorithm for Solving the Server-

consolidation Problem with Conﬂicts. In Proceedings

of the ﬁrst ACM/SIGEVO Summit on Genetic and Evo-

lutionary Computation, pages 1–8, Shanghai, China.

ACM.

Ajiro, Y. and Tanaka, A. (2007). Improving Packing Algo-

rithms for Server Consolidation. In In Proceedings of

the International Conference for the Computer Mea-

surement Group (CMG).

Beloglazov, A., Buyya, R., Lee, Young, C., and Zomaya, A.

(2010). A Taxonomy and Survey of Energy-Efﬁcient

Data centers and Cloud Computing Systems. Tech-

nical report, CLOUDS-TR-2010-3. Cloud Comput-

ing and Distributed Systems Laboratory, University of

Melbourne, Australia.

Clark, C., Fraser, K., Hand, S., Hansen, J. G., Jul, E.,

Limpach, C., Pratt, I., and Warﬁeld, A. (2005). Live

Migration of Virtual Machines. In In Proceedings

of the 2nd conference on Symposium on Networked

Systems Design & Implementation (NSDI05), Vol. 2.

USENIX Association, Berkeley, CA, USA.

Economou, D., Rivoire, S., and Kozyrakis, C. (2006). Full-

System Power Analysis and Modeling for Server En-

vironments. In In Workshop on Modeling Benchmark-

ing and Simulation (MOBS.

Falkenauer, E. and Delchambre, A. (1992). A Genetic Algo-

rithm for Bin Packing and Line Balancing. In IEEE In-

ternational Conference on Robotics and Automation,

pages 1186–1192 vol.2.

Farrahi Moghaddam, F. and Cheriet, M. (2010). Decreasing

Live Virtual Machine Migration Down-Time Using a

Memory Page Selection Based on Memory Change

PDF. In Networking, Sensing and Control (ICNSC),

2010 International Conference on, pages 355–359.

Farrahi Moghaddam, F., Cheriet, M., and Nguyen, K. K.

(2011). Low Carbon Virtual Private Clouds. In

IEEE International Conference on Cloud Comput-

ing (CLOUD’ 11), pages 259–266, Washington, DC,

USA.

Garey, M. R. and Johnson, D. S. (1979). A Guide to

The Theory of NP-Completeness. Technical report,

W.H.Freeman Co., San Francisco.

Gmach, D., Rolia, J., Cherkasova, L., and Kemper, A.

(2009). Resource Pool Management: Reactive Ver-

sus Proactive or Let’s be Friends. Comput. Netw.,

53(17):2905–2922.

Kansal, A., Zhao, F., Liu, J., Kothari, N., and Bhattacharya,

A. A. (2010). Virtual Machine Power Metering and

Provisioning. In Proceedings of the 1st ACM sympo-

sium on Cloud computing, pages 39–50, Indianapolis,

Indiana, USA. ACM.

Liu, L., Wang, H., Liu, X., Jin, X., He, W. B., Wang, Q. B.,

and Chen, Y. (2009). GreenCloud: A New Architec-

ture for Green Data Center. In Proceedings of the

6th international conference industry session on Au-

tonomic computing and communications industry ses-

sion, pages 29–38, Barcelona, Spain. ACM.

McKinsey (2007). The Impact of ICT on Global Emissions.

Technical report, tech. rep., on behalf of the Global

eSustainability Initiative (GeSI).

Van der Merwe, J., Ramakrishnan, K. K., Fairchild, M.,

Flavel, A., Houle, J., Lagar-Cavilla, H. A., and Mulli-

gan, J. (2010). Towards a ubiquitous cloud computing

infrastructure. In 17th IEEE Workshop on Local and

Metropolitan Area Networks (LANMAN), pages 1–6.

Webb, M. (2008). SMART 2020: Enabling the Low Carbon

Economy in The Information Age. In The Climate

Group, London.

Wilcox, D., McNabb, A., and Seppi, K. (2011). Solving

Virtual Machine Packing with A Reordering Group-

ing Genetic Algorithm. In Evolutionary Computation

(CEC), 2011 IEEE Congress on, pages 362–369.

Wood, T., Gerber, A., Ramakrishnan, K. K., Shenoy, P., and

der Merwe, J. V. (2009). The Case for Enterprise-

Ready Virtual Private Clouds. In Proceedings of the

2009 conference on Hot Topics in Cloud Computing

(HotCloud09). USENIX Association, Berkeley, CA,

USA.

Wood, T., Ramakrishnan, K., van der Merwe, J., and

Shenoy, P. (2010). CloudNet: A Platform for Opti-

mized WAN Migration of Virtual Machines. Techni-

cal report, University of Massachusetts Technical Re-

port TR-2010-002.

Xu, J. and Fortes, J. (2010). Multi-Objective Virtual Ma-

chine Placement in Virtualized Data Center Environ-

ments. In In proceedings of the 2010 IEEE/ACM In-

ter. Conference on Green Computing and Communi-

cations & Inter. Conference on Cyber, Physical and

Social Computing, Hangshou, PR of China.

Zhang, Q., Cheng, L., and Boutaba, R. (2008). Cloud Com-

puting: State-of-The-Art and Research Challenges.

Journal of Internet Services and Applications, 1(1):7–

18.

CLOSER2012-2ndInternationalConferenceonCloudComputingandServicesScience

324