DECLUSTERING THE ITRUST SEARCH AND RETRIEVAL

NETWORK TO INCREASE TRUSTWORTHINESS

Christopher M. Badger, Louise E. Moser, P. Michael Melliar-Smith,

Isai Michel Lombera and Yung-Ting Chuang

Departments of Computer Science and of Electrical and Computer Engineering, University of California,

Santa Barbara, CA 93106, U.S.A.

Keywords:

Search, Retrieval, Trustworthiness, Declustering.

Abstract:

The iTrust search and retrieval network aims to provide trustworthy access to information on the Web by mak-

ing it difﬁcult to censor or ﬁlter information. The declustering algorithm, presented in this paper, randomizes

the network in a manner that reduces the clustering, or cliquishness, of the network. This randomization also

reduces the necessary amount of cooperation between nodes by ensuring that a connection to any node is

short-lived and can be replaced with a connection to another node from a large pool of known peers. Thus,

the declustering algorithm reduces the expectation of cooperation among peers, which represents the degree to

which the nodes rely on, or act on, information provided by their peers. In general, the smaller the expectation

of cooperation, the less susceptible the network is to malicious attacks. Simulation results demonstrate that the

declustering algorithm succeeds in randomizing the neighbors of a node in the network and, thus, in reducing

the likelihood of malicious attacks.

1 INTRODUCTION

Peer-to-peer (P2P) networks (Wikipedia, 2011a) have

grown to have large user bases, more than 150 mil-

lion users in recent years (i-Safe America, 2011). To

manage their ever increasing numbers of users, P2P

networks have employed a myriad of clever methods

to increase scalability and efﬁciency. Those methods

often relate to the way in which the peers connect to

each other in the overlay network, or in how the peers

search for information in the network. They usually

depend on some form of centralized management and

control of the overlay network, even when the under-

lying network is peer-to-peer. However, if a network

needs to be resilient to censorship and malicious at-

tacks, those methods might not be appropriate or ade-

quate. The core assumptions that are made in existing

P2P networks do not hold in a P2P network that has

robustness as its primary goal. The assumptions that

a majority of the nodes in a P2P network are coop-

erative, and that only a small minority of the nodes

are subversive, might no longer hold; in fact, just the

opposite might be true.

In response to these concerns, and to reduce de-

pendence on centralized search engines for the Web,

we have created a P2P system called iTrust (Chuang

et al., 2011; Michel Lombera et al., 2011). iTrust is

based on the concept that large companies like Google

and Yahoo! might not be unbiased in the search results

they provide and that alternatives need to be available.

Furthermore, other powerful entities, e.g. repressive

governments, might censor or disable systems, such

as search engines, that are capable of providing unre-

stricted access to information on the Web. To com-

bat these threats, iTrust aims to provide reliable in-

formation search and retrieval that cannot easily be

censored or disabled, as well as a robust network that

is resilient to malicious attacks. iTrust provides these

services by using probabilistic information dissemi-

nation techniques in addition to declustering, a heuris-

tic that iTrust peers can use to help randomize their

neighbors in the overlay network.

The declustering algorithm uses randomization to

reduce the clustering, or cliquishness, of the net-

work. This randomization also reduces the necessary

amount of cooperation between nodes by ensuring

that a connection to any node is short-lived and can

be replaced with a connection to another node from

a large pool of known peers. In other words, using

randomization, the declustering algorithm reduces the

expectation of cooperation among peers, which repre-

sents the degree to which the nodes rely on, or act on,

312

M. Badger C., E. Moser L., Michael Melliar-Smith P., Michel Lombera I. and Chuang Y..

DECLUSTERING THE ITRUST SEARCH AND RETRIEVAL NETWORK TO INCREASE TRUSTWORTHINESS.

DOI: 10.5220/0003908503120322

In Proceedings of the 8th International Conference on Web Information Systems and Technologies (WEBIST-2012), pages 312-322

ISBN: 978-989-8565-08-2

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

information provided by their peers. In general, the

smaller the expectation of cooperation, the less sus-

ceptible the network is to malicious attacks.

The rest of this paper is organized as follows.

Section 2 describes some of the methods commonly

used in P2P networks and discusses why they are not

applicable to a network with iTrust’s objectives. Sec-

tion 3 provides an overview of iTrust, including how

iTrust exploits randomization to distribute metadata

and requests for information. Section 4 introduces

our novel declustering algorithm, which can be used

to maintain certain properties of iTrust’s overlay

network. Section 5 includes results from simulations

of iTrust with the declustering algorithm, for several

different kinds of networks and analyzes their sig-

niﬁcance with respect to the goals of iTrust. Finally,

Section 6 presents conclusions and future work.

2 RELATED WORK

2.1 P2P Networks

Although most P2P networks have some similarities,

they are often differentiated by two key factors: cen-

trality and structure.

Centrality is the degree to which a network relies

on speciﬁc nodes. A network is centralized if it re-

quires a single dedicated server to function, whereas

a network is a pure P2P network (the opposite of cen-

tralized) if all nodes are of equal importance. In be-

tween these two kinds of P2P networks are hybrid

P2P networks, which might have a hierarchy of nodes

where the nodes at different levels of the hierarchy

have different levels of importance. One of the ﬁrst

and best known examples of a hybrid P2P network is

the enhanced Gnutella network (Gnutella, 2000; Rasti

et al., 2006), which is discussed in more detail below

Structure is the extent to which the P2P overlay

network is managed. Management can be as sim-

ple as a set of rules governing connections between

nodes, or as complex as an environment that guaran-

tees where information resides in the network. Net-

works in which the overlay network is heavily con-

trolled are referred to as structured, whereas networks

with little or no control over the overlay network

are referred to as unstructured. An example of a

structured P2P network is the Chord network (Stoica

et al., 2001); Chord employs a Distributed Hash Table

(DHT), which is discussed in more detail below.

2.1.1 Gnutella

Gnutella (Gnutella, 2000) with its enhancements

(Rasti et al., 2006) is of interest, because it can be

classiﬁed as a hybrid P2P network. Although the

network is decentralized, it has so-called ultrapeer

nodes that form a backbone for the other nodes. Ul-

trapeers are more or less regular nodes that have sufﬁ-

cient computation and communication resources and

that choose to promote themselves to ultrapeer status.

On reaching ultrapeer status, a node connects itself to

other ultrapeers in order to extend the backbone. An

ultrapeer collects data about its leaf (non-ultrapeer)

neighbors, so that it can propagate queries, and so

that it can respond to queries in the leaf node’s stead,

passing a message to a leaf node only when necessary.

This combination of roles dramatically increases the

scalability of the Gnutella network.

However, this convenience comes at a cost. Ultra-

peers become prime targets for attacks, because the

loss of an ultrapeer can disproportionately harm the

network. Moreover, if a node connects to only ma-

licious ultrapeers, it can become completely isolated

from the rest of the network. Of these two vulnera-

bilities, the former reduces the robustness of the net-

work to targeted attacks (Albert et al., 2000), whereas

the latter allows for easier censorship. The Gnutella

network has enjoyed a large measure of success; how-

ever, these characteristics make it unsuitable as a net-

work whose primary objective is trustworthy informa-

tion search and retrieval, without censorship or ﬁlter-

ing of information.

2.1.2 Freenet

Another P2P network of interest, especially because

its goals are similar to those of iTrust, is Freenet

(Clarke et al., 2000). Like iTrust, Freenet is con-

cerned with limiting censorship by providing a means

for information to be accessed reliably in a distributed

manner. It attempts to achieve this goal by using its

own routing protocol, which routes requests to nodes

that have been observed to do well with similar re-

quests. An advantage of the Freenet routing proto-

col is that it does not require any network-wide in-

formation or structure to be applied by an individual

node; the same is true of the iTrust declustering al-

gorithm, which attempts to randomize nodes in the

network and reduce the severity of malicious attacks.

Although both techniques are used to increase the ef-

fectiveness of their respective P2P networks, the aim

of iTrust’s declustering algorithm along with proba-

bilistic search is to mitigate the effects of malicious

attacks, whereas Freenet’s routing protocol provides

efﬁcient routing but might be overly optimistic when

considering the number of possibly malicious nodes

present in the network.

DECLUSTERINGTHEITRUSTSEARCHANDRETRIEVALNETWORKTOINCREASETRUSTWORTHINESS

313

2.1.3 Distributed Hash Tables

Another common approach to building P2P networks

involves the use of an organizational structure called a

Distributed Hash Table (DHT), such as that of Chord

(Stoica et al., 2001). In essence, DHTs use a speciﬁc

type of function that maps a keyspace onto the nodes

in the network. Every node in the network becomes

responsible for a set of keys that are mapped to it.

Clever mappings are used to create a strict ordering

between keys and the nodes responsible for the keys,

allowing the node responsible for a key and the target

information to be found quickly. Moreover, when a

node joins or leaves the network, only adjacent nodes

are affected, where adjacency is determined by the or-

dering of the key/value pairs. This last property mini-

mizes the work necessary during network churn, joins

and leaves, and provides excellent scalability.

Despite these advantages, DHTs have a signiﬁcant

weakness in that, if a malicious node gains control

over a target area of the keyspace, it becomes respon-

sible for a portion of the keys in the network and can

refuse searches based on those keys. This vulnerabil-

ity enables an attacker to take a strategic position in

the network and censor a particular key or set of keys.

Although DHTs are often used in completely decen-

tralized networks that, otherwise, are difﬁcult to at-

tack, the ability to censor speciﬁc information is the

problem that iTrust is designed to defeat.

2.2 Random Networks

Much research has been done on random networks,

and two properties have emerged, the small-world ef-

fect and the power-law degree distribution.

The small-world effect is the property that there

exist short paths between any pair of nodes in the net-

work. Many years ago (Milgram, 1967), it was shown

that the small-world effect applies to social networks,

and that individuals are adept at ﬁnding such short

paths using only their local neighborhood informa-

tion. We aim for a similar effect in iTrust. A node

maintains connections to only a small number of peer

nodes, which form its neighborhood. The neighbors

of a node forward messages generated by the node to

their neighbors.

The power-law degree distribution (Wikipedia,

2011b) is the property that the probability of the node

degree varies as a power of the degree. This property

results when networks expand continuously by the ad-

dition of new nodes, and new nodes attach preferen-

tially to already well-connected nodes (Barab

asi and

Albert, 1999). Power law networks concentrate many

connections at a relatively small number of nodes,

which is a disadvantage for iTrust, because malicious

manipulation of such highly connected nodes might

distort the distribution of information. iTrust aims for

networks in which all nodes are equal, which will not

happen by chance but is an explicit objective of iTrust.

To comply with both the small-world effect and

the power-law degree distribution, several researchers

(Makowiec, 2005; Ree, 2006) proposed rewiring a

constant-size network based on the preferential at-

tachment of new nodes to already well-connected

nodes. Likewise, in our declustering algorithm, we

consider a relatively small neighborhood of a node

and rewire it, but for the purposes of achieving ran-

domization and resistance to malicious attacks.

In our experiments and results presented in Sec-

tion 5, we consider the Erd

os-R

enyi, Barab

asi-Albert,

and Watts-Strogatz networks in the context of our

declustering algorithm for iTrust. We brieﬂy intro-

duce these networks below.

2.2.1 Erd

os-R

enyi Network

The Erd

os-R

enyi network is a classic random net-

work, where any two nodes are connected accord-

ing to a ﬁxed probability. Because every edge has

an equal chance of existing, independent of all other

edges, the degree of any node follows a binomial dis-

tribution (Erd

os and R

enyi, 1960).

2.2.2 Watts-Strogatz Network

The Watts-Strogatz network is initially constructed by

placing nodes on one or more dimensional regular lat-

tices, e.g. circle or grid, and connecting each node

to its n nearest neighbors. Furthermore, the model

adds random rewiring of edges so that the resulting

network has a small diameter (Watts and Strogatz,

1998). Real networks have been observed to have

small diameters (Travers and Milgram, 1969). When

the rewiring probably is chosen to be zero, the net-

work is identical to the original lattice.

2.2.3 Barab

asi-Albert Network

The Barab

asi-Albert network is created incrementally

by preferentially attaching new nodes to already well-

connected nodes (Barab

asi and Albert, 1999). This

process leads to a graph with a power-law degree dis-

tribution. Many real networks have degrees that fol-

low a heavy-tail power law degree distribution.

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

314

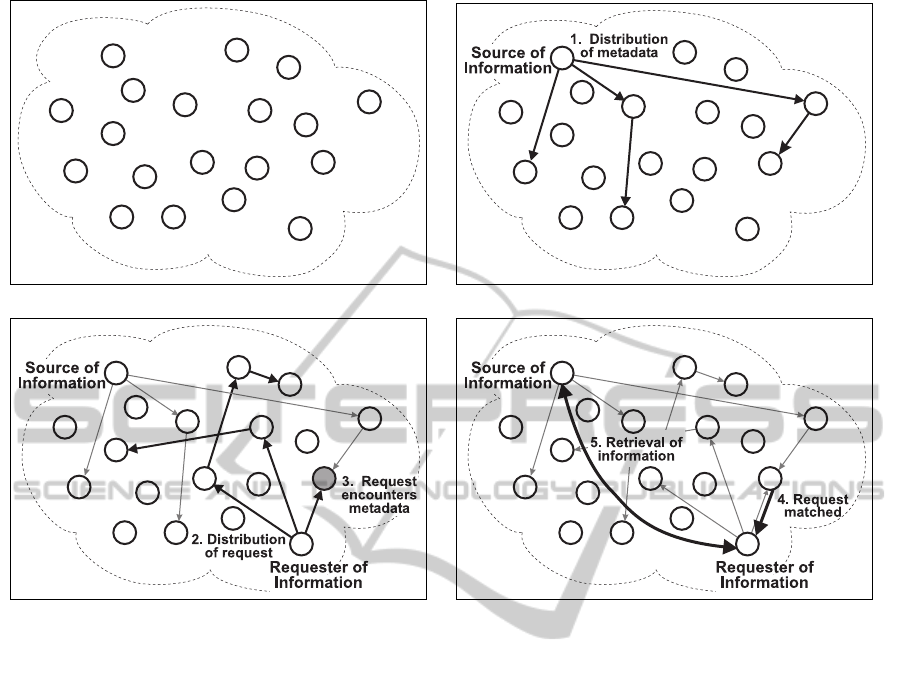
(a) A network with participating nodes. (b) A source node distributes metadata.

Figure 1: The iTrust random, probabilistic search strategy.

3 THE ITRUST P2P NETWORK

To address potential Internet censorship and other

problems associated with centralized search engines,

as well as to avoid the aforementioned P2P network

vulnerabilities, we are developing the iTrust P2P net-

work (Chuang et al., 2011; Michel Lombera et al.,

2011). iTrust is intended to be robust against attacks

as well as capable of disseminating information even

in the presence of attempts to suppress it, i.e., iTrust

is intended to be censorship resistant. iTrust attains

these goals by making use of a random, probabilistic

search strategy.

The nodes that participate in an iTrust network are

referred to as the participating nodes or the member-

ship (Figure 1(a)). Some of the participating nodes,

the source nodes, produce information, and make

that information available to other participating nodes

(Figure 1(b)). The source nodes also produce meta-

data that describes their information, and distribute

the metadata, along with the URL of the information,

to a subset of the participating nodes chosen at ran-

dom. Other participating nodes, the requesting nodes,

request and retrieve information. Such nodes gener-

ate requests that contain keywords, and distribute the

requests to a subset of the participating nodes chosen

at random (Figure 1(c)). Nodes that receive a request

compare the keywords in the request with the meta-

data they hold. If a node ﬁnds a match, which we

call an encounter, the matching node returns the URL

of the associated information to the requesting node

(Figure 1(d)). The requesting node then uses the URL

to retrieve the information from the source node. A

match between the keywords in a request received by

a node and the metadata held by the node might be an

exact match or a partial match, or might correspond

to synonyms.

In iTrust, each node maintains a list of cooperat-

ing peers, nodes that distribute metadata and that is-

sue search requests. Every node needs such a list from

which to draw random subsets of nodes for distribu-

tion of metadata and requests. In our existing im-

plementation of iTrust (Chuang et al., 2011; Michel

Lombera et al., 2011), all nodes maintain a list of sub-

DECLUSTERINGTHEITRUSTSEARCHANDRETRIEVALNETWORKTOINCREASETRUSTWORTHINESS

315

stantially all participating nodes, which works quite

well for memberships of a few hundred or thousand

participating nodes. For memberships of millions of

participating nodes, the cost of the membership list,

and the cost of maintaining the membership, as nodes

join and leave the membership, can become exces-

sive. Consequently, in this paper, we investigate P2P

networks in which each node holds a list of partici-

pating nodes that form a small, random subset of the

membership, i.e., a neighborhood of the node. Be-

cause it can be difﬁcult to ascertain whether a given

node is cooperative or malicious, we must ensure that

the subset is sufﬁciently random. By making a ran-

dom choice of a subset from the list of known partic-

ipating nodes, attempts to poison the list with a large

number of malicious nodes can be mitigated.

Even unstructured networks, such as iTrust, can

develop many unwanted features when left to their

own devices. Real networks tend to form cliques

and have degree distributions that follow a power

law (Adamic et al., 2001; Watts and Strogatz, 1998).

Cliques are undesirable, because they can decrease

the efﬁcacy of searches and can compartmentalize

the network. Degree distributions that follow power

laws tend to have a few hub nodes that become single

points of failure, which is a real problem for hybrid

hierarchical P2P networks. Because of these char-

acteristics of real networks, it is useful to create a

method that can be applied to a network to inﬂuence

its structure towards a more robust, random variant.

Moreover, it is of utmost importance that this method

is fully distributed and is applicable at the individual

node level, and that it does not require global context

or understanding of the entire network.

4 DECLUSTERING

4.1 Expectation of Cooperation

Traditional strategies for P2P overlay networks de-

pend on a high level of cooperation between peers in

the network, and degrade rapidly if cooperation is in-

sufﬁcient. Our declustering algorithm aims to achieve

a high level of functionality even at lower levels of co-

operation between peers. It is based on the idea that

there is an expectation of cooperation between peers

in the network, which represents the degree to which

nodes rely on, or act on, information provided by their

peers. The expectation of cooperation can be thought

of as the set of assumptions made during peer commu-

nication, e.g., that the information provided by other

nodes is trustworthy. In general, the smaller the ex-

pectation of cooperation, the less dependence there is

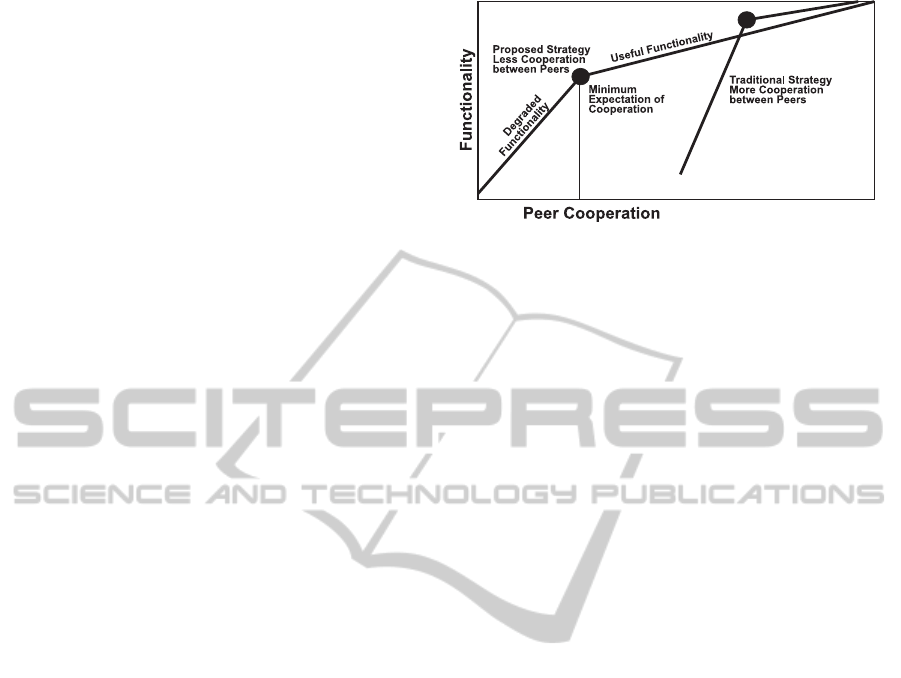
Figure 2: The minimum expectation of cooperation can be

imagined as the point at which network functionality begins

to degrade rapidly.

to exploit, and the less susceptible the network is to

attack. Thus, by decreasing the expectation of coop-

eration between peers in the network, the robustness

of the network can be improved.

Moreover, an individual node should not require

a given level of cooperation from its neighbors but,

rather, it should require a given level of cooperation

from the network. That is, the expectation of coop-

eration should be not only as small as possible, but

also as focused on the network as possible, rather

than on a subset of the participating nodes. Figure 2

shows the traditional strategy and our proposed strat-

egy, which achieves a high level of functionality even

at lower levels of cooperation between peers. The ﬁg-

ure shows the minimum expectation of cooperation,

i.e., the point below which network functionality be-

gins to degrade rapidly.

The inability to use more advanced search tech-

niques that rely on a greater expectation of coopera-

tion is partially offset in iTrust by probabilistic search

techniques that make even message ﬂooding scalable

(Banaei-Kashani and Shahabi, 2003).

4.2 Deﬁnitions

For our declustering algorithm, we represent the net-

work as an undirected graph, where the nodes in the

graph correspond to nodes in the network and the

edges in the graph correspond to connections between

the nodes in the network. The degree of a node is the

number of edges emanating from it. We use the fol-

lowing terminology in our descriptions of the declus-

tering algorithm, the simulation, and the results.

A neighbor of a node is a node that is directly con-

nected to the node, i.e., such that there exists an edge

between the two nodes. The neighborhood of a node

comprises all of the neighbors of the node, i.e., all of

the nodes to which the node is directly connected. A

neighborhood is a random, small subset of the mem-

bership of the iTrust network, as shown in Figure 3.

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

316

Figure 3: A large membership with small neighborhoods about a source node and a requesting node.

The network view of a node is the number of the

node’s neighbors plus the number of the neighbor’s

neighbors. Our concept of the network view is taken

from Gossple (Jelasity et al., 2007; Bertier et al.,

2010), where the idea is used in peer management.

A clique is a group of nodes that are highly con-

nected among themselves. The global clustering co-

efﬁcient of a network measures the “cliquishness” of

the network, i.e., how common and how large the

cliques in the network are. In our declustering al-

gorithm, we use the Watts-Strogatz version of the

global clustering coefﬁcient, the calculation of which

is given in Figure 7.

A hub is a node with a signiﬁcantly higher than av-

erage degree. The hub degree is the number of edges

emanating from the hub, i.e., the number of nodes to

which the hub is directly connected.

The network diameter is the distance between the

two nodes in the network that are farthest apart. More

formally, the network diameter is the largest path

length of all of the shortest paths in the solution for

the all pairs shortest paths problem.

The match probability is the probability that a re-

questing node receives one or more responses from

nodes that hold metadata that matches the keywords

in its request.

4.3 The Declustering Algorithm

Our declustering algorithm can be used to assuage

the potential problems, introduced by real networks

and malicious attackers, through randomization of the

neigborhoods of the nodes, i.e., the connections made

by the nodes. The algorithm is so named because its

main purpose is to reduce the global clustering coefﬁ-

cient of the graphs to which it is applied. The declus-

tering algorithm can be used by any individual node

in the network, which makes it particularly useful if

cooperation between nodes is expected to be minimal.

The basic idea of the declustering algorithm is pre-

sented in Figures 4 and 5. A node makes a list of all of

its neighbors and all of its neighbor’s neighbors and

then randomly selects new neighbors from the com-

bined list. If applied enough times and by different

nodes, the desired end result is that the network will

become “sufﬁciently random.” Declustering might be

seen as an attempt to de-structure the network by re-

moving any patterns or trends that are present in it.

In the iTrust network with the declustering algo-

rithm, we assume that there are N participating nodes

in the membership and n participating nodes in a

neighborhood of a node. A source node distributes

its metadata to m participating nodes in its current

neighborhood, and a requesting node distributes its

request to r participating nodes in its current neigb-

horhood. If the nodes choose nodes for their neigh-

borhoods at random and if the source nodes (request-

ing nodes) distribute their metadata (requests) at ran-

dom to the nodes in their neighborhoods, then the

metadata (requests) are distributed at random to the

participating nodes in the iTrust membership. If m

and r are sufﬁciently large with respect to N, then the

probability of one or more matches is high. For exam-

ple, if N = 1000 participating nodes, n = 150 partic-

ipating nodes, the metadata are distributed to m = 50

participating nodes, and the requests are distributed

to r = 50 participating nodes, then the probability of

one or more matches is p = 0.928023, which we ob-

tain using the formula given in (Chuang et al., 2011;

Michel Lombera et al., 2011).

5 SIMULATION AND RESULTS

5.1 Metrics

To analyze the results of our simulation quantitatively,

DECLUSTERINGTHEITRUSTSEARCHANDRETRIEVALNETWORKTOINCREASETRUSTWORTHINESS

317

1. For any given node X, place all of X’s neighbors, and X ’s neighbor’s neighbors into a set S.

• In the set S, duplicate entries are not allowed, and each node occurs only once. After the ﬁrst step is

complete, S is the set of all nodes that are visible to the node.

2. Remove all edges incident to X, in effect clearing its neighborhood.

3. Select M new neighbors from S without replacement, where M is the number of neighbors that node X

originally had. Alternatively, randomly select each node in S with probability

|S|

, to obtain a binomial

distribution with mean M.

• The latter method allows each node to vary the number of neighbors it has, but to retain roughly

the same number of neighbors. However, doing so leads to an increassed variance in the degree

distribution of the network, and is not used in our simulations.

Figure 4: The declustering algorithm.

(a) Initial neighbors. (b) Discover nodes. (c) Drop neighbors. (d) Pick new neighbors.

Figure 5: Example of the declustering algorithm.

we recorded the following metrics: the maximum hub

degree, the average network view, the global cluster-

ing coefﬁcient, the average network diameter, and the

match probability.

Determining the maximum hub degree is simply a

matter of ﬁnding the most highly connected node in

the network. The average network view is also easy

to calculate by averaging the network views of ev-

ery node during the declustering process. The global

clustering coefﬁcient is not as easy to calculate. We

use the Watts-Strogatz version of the global cluster-

ing coefﬁcient; it is deﬁned as the average of the

local clustering coefﬁcients of all nodes in the net-

work. The local clustering coefﬁcient calculation is

described in Figure 7. The experiments related to

the network diameter were performed separately from

those for the other metrics.

5.2 Simulation

Because the declustering algorithm requires a graph

as input, and the structure of the graph can affect the

results of the declustering, we input three different

types of graphs to the algorithm multiple times, the

Erd

os-R

enyi graph, the Barab

asi-Albert graph, and

the Watts-Strogatz graph, shown in Figure 6.

For the hub degree, network view, clustering co-

efﬁcient and match probability, we performed the

following steps. First, we created the initial net-

work graph and recorded information about it. Then,

we applied our declustering algorithm to the graph

in several successive passes. In the ﬁrst pass, the

declustering algorithm is applied to the original graph

and information about the once declustered graph

is recorded. In the second pass, the declustering

algorithm is applied to the once declustered graph

and information about the twice declustered graph is

recorded. In the third pass, the declustering algorithm

is applied to the twice declustered graph and informa-

tion about the thrice declustered graph is recorded.

For the network diameter, we performed separate

experiments from those for the other metrics. First,

we created the initial network graphs for each model

and then we removed the nodes with the most con-

nection, one-by-one, until the diameter of the network

increased. We then recorded the number of nodes re-

quired to be removed before the diameter changed.

This number is used as a gauge to determine the

amount of work required to harm the network.

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

318

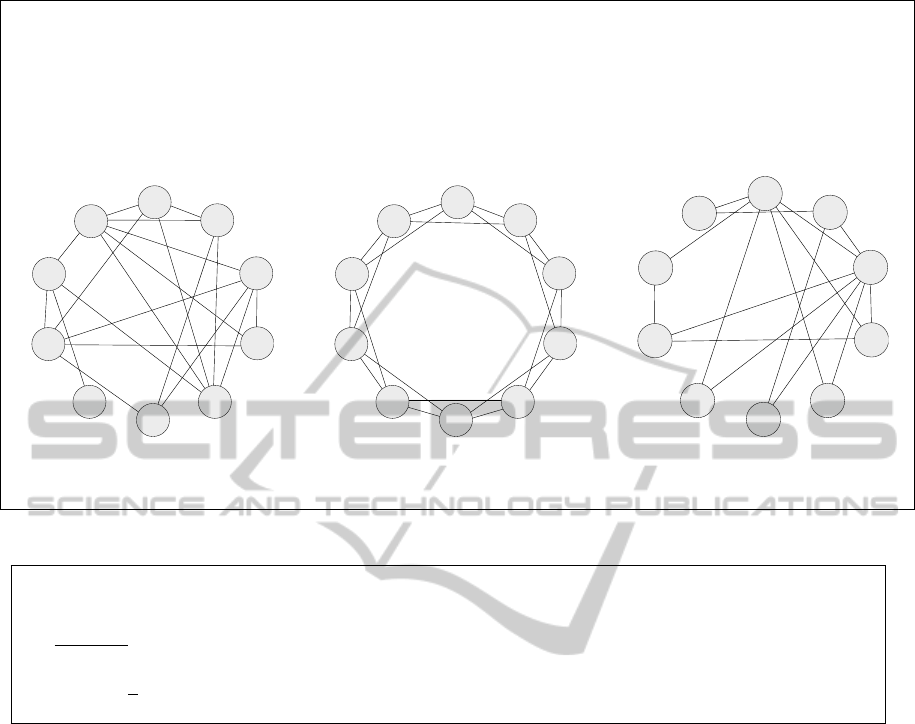
Erd

os-R

enyi Graph (Erd

os and R

enyi, 1960): Has very low clustering coefﬁcients and is very robust to random

and targeted failures. Used as the baseline.

Watts-Strogatz Graph (Watts and Strogatz, 1998): Has very high clustering coefﬁcients. Used to investigate

the ability of declustering to lower clustering coefﬁcients.

Barab

asi-Albert Graph (Barab

asi and Albert, 1999): Node degrees follows a power law distribution, which

results in the formation of a few very large hubs. Used to investigate the ability of declustering to remove

hubs and smooth out the node degree distribution curve.

(a) Erd

os-R

enyi graph(P = 0.4) (b) Watts-Strogatz graph

(K = 4, β = 0.0)

asi-Albert graph

(m = m

= 2, a = 1)

Figure 6: Three types of random graphs with n = 10.

1. To calculate the local clustering coefﬁcient of node X, put all of X’s neighbors into a set S.

2. Find E, the number of possible edges between all nodes in S. For an undirected graph, this number is

|S|×(|S|−1)

3. Find e, the number of edges that exist between nodes in S. The local clustering coefﬁcient for node X is

given by

. Note that this quantity is always less than or equal to 1.

Figure 7: Algorithm for calculating the local clustering coefﬁcient.

5.3 Results

5.3.1 Hub Degree, Network View, Clustering

Coefﬁcient, Match Probability

The results of the simulation of iTrust with the

declustering algorithm for the hub degree, network

view, clustering coefﬁcient, and match probability are

shown in Table 1. These results were obtained for an

iTrust network with a membership of N = 1000 par-

ticipating nodes and with neighborhoods that contain

n = 150 participating nodes, where the metadata are

distributed to m = 50 nodes within the neighborhood

of a source node and the requests are distributed to

r = 50 nodes within the neighborhood of a requesting

node. The table shows the results of the simulation of

iTrust for three passes of the declustering algorithm

for the three graphs.

First and foremost, one of the most interesting yet

somewhat expected results is that the metrics for the

Erd

os-R

enyi graph change very little despite declus-

tering. The reason is that the declustering process

very nearly emulates the construction of the Erd

os-

enyi graph — it attempts to distribute edges in

the graph at random. Declustering also causes the

other graphs to transform slowly into Erd

os-R

enyi-

like graphs, as is shown for the Watts-Strogatz and

Barab

asi-Albert graphs. The global clustering co-

efﬁcient of the Watts-Strogatz graph, with an edge

rewiring probability of 0, is very quickly reduced.

Even after a single declustering pass, its global clus-

tering coefﬁcient is consistent with that of the Erd

os-

enyi graph.

This effect is noteworthy because of the fact that

real networks tend to have larger global clustering co-

efﬁcients than Erd

os-R

enyi graphs and, thus, can ex-

hibit sub-optimal performance using iTrust’s search

and retrieval strategy, due to their increased cluster-

ing. In networks similar to the Watts-Strogatz graph,

declustering not only increases the match probability

DECLUSTERINGTHEITRUSTSEARCHANDRETRIEVALNETWORKTOINCREASETRUSTWORTHINESS

319

Table 1: Results of the simulation of iTrust with the declustering algorithm.

Maximum Average Global Match

Hub Network Clustering Probability

Degree View Coefﬁcient

Erd

os-R

enyi Graph

Initial 192 1000 0.1502 0.9282

1st Pass 187 1000 0.1501 0.9283

2nd Pass 187 1000 0.1501 0.9282

3rd Pass 190 1000 0.1499 0.9279

Watts-Strogatz Graph

Initial 150 301 0.7450 0.2858

1st Pass 187 1000 0.1506 0.9286

2nd Pass 185 1000 0.1503 0.9283

3rd Pass 180 1000 0.1501 0.9290

Barab

asi-Albert Graph

Initial 492 1000 0.2399 0.9652

1st Pass 246 1000 0.1533 0.9297

2nd Pass 187 1000 0.1505 0.9281

3rd Pass 186 1000 0.1508 0.9283

Table 2: More results of the simulation of iTrust with the declustering algorithm.

Network Diameter 4 5 6 7 8

Average Number of High-Degree Nodes Removed

Erd

os-R

enyi Graph 270 352 374 386 394

Watts-Strogatz Graph 207 329 366 378 389

Barab

asi-Albert Graph 112 236 274 307 331

Barab

asi-Albert Graph 259 342 363 380 388

Once Declustered

of iTrust but also ensures sufﬁcient network edge ran-

domness to decrease the possibility of malicious at-

tacks in the network.

In the same vein, the large hubs of the Barab

asi-

Albert graph are a potential vulnerability despite the

fact that they increase the search success rate. In

this case, the ability of declustering to remove hubs

and smooth the node degree distribution curve is ex-

tremely useful for increasing the robustness of the net-

work. Real networks tend to have degree distributions

that follow a power law (Adamic et al., 2001; Price,

1976), and hubs similar to those of the Barab

asi-

Albert graphs.

5.3.2 Network Diameter

The results of the simulation of iTrust with the declus-

tering algorithm for the network diameter are shown

in Table 2. These results were obtained for an iTrust

network with a membership of N = 500 nodes and

with neighborhoods of n = 50 nodes on average. The

table shows, for each network and for network diam-

eter between 4 and 8, the number of nodes that had to

be removed before the diameter changed to the net-

work diameter shown.

Each removal disabled the node in the network

with the highest degree and removed all of its con-

nections to other nodes. Because networks with small

diameters are preferable, the results show that the

structure of the Barab

asi-Albert graph is less robust

against targeted attacks than the Erd

os-R

enyi graph.

Moreover, the Barab

asi-Albert graph exhibits a no-

ticeable improvement in robustness after only a sin-

gle declustering pass. The difference in performance

between these two graphs is most likely due to the

uneven distribution of edges in the Barab

asi-Albert

graph, which allows a larger proportion of edges to be

removed from the network with the removal of a hub.

For the Watts-Strogatz graph, with N = 500, n =

50 and an edge rewiring probability of 0, as used in

Table 1, the diameter is initially 10 due to its ring

lattice structure. Therefore, for the network diameter

experiments, we used an edge rewiring probability of

0.1 instead, which gave the initial network a diameter

more comparable to that of the other networks. This

version of the Watts-Strogatz graph ended up splitting

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

320

the difference between the Barab

asi-Albert graph and

the Erd

os-R

enyi graph in terms of robustness.

6 CONCLUSIONS

We have described a declustering algorithm for the

iTrust search and retrieval network. The objective of

iTrust is to provide trustworthy access to information

on the Web by making it difﬁcult to censor or ﬁlter in-

formation. The declustering algorithm decreases the

expectation of cooperation between peers in the iTrust

network and, thus, improves the robustness of the net-

work. The expectation of cooperation represents the

degree to which the nodes rely on, or act on, informa-

tion provided by their peers.

The simulation results demonstrate that the

declustering algorithm succeeds in randomizing the

neighbors of a node. This randomness not only helps

mitigate malicious attacks, but also allows for eas-

ier analysis of the functionality of the network. The

simulation results also show that even networks with

high global clustering coefﬁcients or extremely large

hubs can be transformed into Erd

os-R

enyi-like graphs

very quickly when declustering is used. In some

cases, only one pass is required to achieve the de-

sired outcomes of lower global clustering coefﬁcients

and fewer nodes with high degrees. These ﬁndings

support the idea that techniques applied on a node-

by-node basis can be used to ensure certain network-

wide properties in pure P2P networks, both unstruc-

tured and loosely structured.

While declustering might be useful for iTrust, and

its objective of preventing censorship or ﬁltering of

information accessed over the Web, it might not be

useful for P2P networks that have different objec-

tives. The declustering technique might sacriﬁce po-

tentially useful network features; however, it accom-

plishes its goal of making the network more robust.

Subsequent versions of iTrust might use information

gathered from forwarded queries to help in the declus-

tering process. Future work in this area might inves-

tigate other techniques like declustering that work to

create robust networks by supporting and promoting

high levels of network churn.

ACKNOWLEDGEMENTS

This research was supported in part by U.S. Na-

tional Science Foundation grant number NSF CNS

10-16193 and by an REU supplement to support the

ﬁrst author.

REFERENCES

Adamic, L. A., Lukose, R. M., Puniyani, A. R., and Hu-

berman, B. A. (2001). Search in power-law networks.

Physical Review E, 64(046135):046135–1–046135–8.

Albert, R., Hawoong, J., and Barab

asi, A. (2000). Error

and attack tolerance of complex networks. Nature,

406(6794):378–382.

Banaei-Kashani, F. and Shahabi, C. (2003). Criticality-

based analysis and design of unstructured peer-to-peer

networks as complex systems. In Proceedings of the

IEEE International Symposium on Cluster Computing

and the Grid, page 351.

Barab

asi, A. and Albert, R. (1999). Emergence of scaling

in random networks. Science, 286:509–512.

Bertier, M., Frey, D., Guerraoui, R., Kermarrec, A. M., and

Leroy, V. (2010). The Gossple anonymous social net-

work. In Proceedings of the ACM/IFIP/USENIX 11th

Middleware Conference, pages 191–211.

Chuang, Y. T., Michel Lombera, I., Moser, L. E., and

Melliar-Smith, P. M. (2011). Trustworthy distributed

search and retrieval over the Internet. In Proceed-

ings of the 2011 International Conference on Internet

Computing, pages 169–175.

Clarke, I., Sandberg, O., Wiley, B., and Hong, T. (2000).

Freenet: A distributed anonymous information stor-

age and retrieval system. In Proceedings of the Inter-

national Workshop on Designing Privacy Enhancing

Technologies: Design Issues in Anonymity and Unob-

servability, pages 46–66.

Erd

os, P. and R

enyi, A. (1960). On the evolution of random

graphs. Publication of the Mathematical Institute of

the Hungarian Academy of Sciences, 5:17–61.

Gnutella (2000). http://gnutella.wego.com/.

i-Safe America (2011). Peer-to-peer networking.

http://www.isafe.org/imgs/pdf/education/P2PNetwork

ing.pdf.

Jelasity, M., Voulgaris, S., Guerraoui, R., Kermarrec, A. M.,

and van Steen, M. (2007). Gossip-based peer sam-

pling. ACM Transactions on Computer Systems,

25(8).

Makowiec, D. (2005). Evolving network–simulation study.

The European Physical Journal B–Condensed Matter

and Complex Systems, 48:547–555.

Michel Lombera, I., Chuang, Y. T., Melliar-Smith, P. M.,

and Moser, L. E. (2011). Trustworthy distribution and

retrieval of information over HTTP and the Internet.

In Proceedings of the Third International Conference

on the Evolving Internet, pages 7–13.

Milgram, S. (1967). The small world problem. Psychology

Today, 2:60–67.

Price, D. D. S. (1976). A general theory of bibliometric

and other cumulative advantage processes. Journal of

the American Society for Information Science, pages

292–306.

Rasti, A. H., Stutzbach, D., and Rejaie, R. (2006). On the

long-term evolution of the two-tier Gnutella overlay.

In Proceedings of the 25th IEEE International Con-

ference on Computer Communications, pages 1–6.

DECLUSTERINGTHEITRUSTSEARCHANDRETRIEVALNETWORKTOINCREASETRUSTWORTHINESS

321

Ree, S. (2006). Power-law distributions from addi-

tive preferential redistributions. Physical Review E,

73:026115.

Stoica, I., Morris, R., Karger, D., Kaashoek, F. M., and Bal-

akrishnan, H. (2001). Chord: A scalable peer-to-peer

lookup service for Internet applications. In Proceed-

ings of the 2001 ACM Conference on Applications,

Technologies, Architectures and Protocols for Com-

puter Communications, pages 149–160.

Travers, J. and Milgram, S. (1969). An experimental study

of the small world problem. Sociometry, 32(4):425–

443.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of ‘small-world’ networks. Nature, 393(6684):440–

442.

Wikipedia (2011a). Peer-to-peer networks. http://en.wikipe

dia.org/wiki/peer-to-peer.

Wikipedia (2011b). Power law networks. http://en.wikiped

ia.org/wiki/power law.

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

322