
INTEGRATING COMPUTATIONAL THINKING WITH K-12
SCIENCE EDUCATION
A Theoretical Framework
Pratim Sengupta
1, 3
, John S. Kinnebrew
2
, Gautam Biswas
2
and Douglas Clark
3
1
Mind, Matter and Media Lab, Vanderbilt University, Nashville, Tennessee, U.S.A.
2
Department of EECS/ISIS, Vanderbilt University, Nashville, Tennessee, U.S.A.
3
Department of Teaching and Learning, Peabody College, Vanderbilt University, Nashville, Tennessee, U.S.A.
Keywords: Computational Thinking, Agent-based Modelling and Simulation, Visual Programming, Constructionism,
Learning by Design, Explanation and Argumentation, Computational Modelling.
Abstract: Computational thinking (CT) draws on concepts that are fundamental to computing and computer science,
however, as an approach, it includes practices, such as problem representation, abstraction, decomposition,
simulation, verification, and prediction that are also central to modelling, reasoning, and problem solving in
many scientific and mathematical disciplines. Recently, arguments have been made in favour of integrating
programming and CT with K-12 curricula. In this paper, we present a theoretical investigation of key issues
that need to be considered for integrating CT with K-12 science. We identify the synergies between pro-
gramming and CT on one hand, and scientific expertise on the other. We then present a critical review of
literature on educational computing, and propose a set of guidelines for designing learning environments in
science that can jointly foster the development of computational thinking with scientific expertise. Finally,
we describe the design of a learning environment that supports CT through modelling and simulation to help
middle school students learn physics and biology.
1 INTRODUCTION
Wing (2006, 2008) and others (NRC, 2010) have de-
scribed computational thinking as a general, analytic
approach to problem solving, designing systems, and
understanding human behaviours. Computational
thinking (CT) draws on concepts that are fundamen-
tal to computing and computer science, however, as
an approach, it includes practices (e.g., problem rep-
resentation, abstraction, decomposition, simulation,
verification, and prediction) that are also central to
modelling, reasoning, and problem solving in a large
number of scientific and mathematical disciplines
(NRC, 2010). Several scholars (Soloway, 1993);
(diSessa, 1986, 2000); (Sherin, 2000); (Pea, 1986);
(Guzdial, 1995) have used the synergies between
scientific thinking, analysis and engineering design,
and evaluation to establish close links between CT
and modeming, reasoning, and problem solving in
STEM disciplines.
Developing scientific reasoning and expertise
requires sustained, immersive educational
experiences, as is reflected in the recent efforts to
develop learning progressions for science in K-12
classrooms (Lehrer, Schauble, and Lucas, 2008;
Krajick et al., 2008). Similarly, fostering a
curriculum that integrates CT with science and
mathematics requires the design of coherent, long-
term curricula (ACM K-12 Taskforce, 2003).
However, there exists no theoretical framework that
can support such an endeavour, and empirical
studies show that integrating computational
modelling and programming with K-12 science and
math curricula can be extremely challenging (Sherin
et al., 1992). Our goal in this paper is to establish
such a framework and present the design of a
computer-based learning environment, which
supports middle school science learning through
Computational Thinking in Simulation and Model-
building (CTSiM).
40
Sengupta P., S. Kinnebrew J., Biswas G. and Clark D..
INTEGRATING COMPUTATIONAL THINKING WITH K-12 SCIENCE EDUCATION - A Theoretical Framework.
DOI: 10.5220/0003915500400049
In Proceedings of the 4th International Conference on Computer Supported Education (CSEDU-2012), pages 40-49
ISBN: 978-989-8565-07-5
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 REVIEW OF LITERATURE ON
EDUCATIONAL COMPUTING
Table 1: Computational thinking and STEM expertise.
Computational
Thinking and
Programming
STEM Expertise
Abstractions
Models, laws and other generalizable
representations in science; Variables and
functional forms in mathematics
Encapsulation
Creating coherent, formal representations
of scientific processes and phenomena;
Understanding functions as dynamic ob-
jects in mathematics
Classes/Agents and
Class Inheritance
Agent-based thinking (micro-level rea-
soning, species vs. individuals, classifi-
cation and hierarchy – inheritance)
Emergence and
Aggregation
Macro-level reasoning;
Generating aggregate-level equations
and functional forms from individual-
level variables
Algorithms
(Behaviours) and
Causal Reasoning
(Interactions and
Rules)
Mechanistic reasoning; Natural laws;
Mathematical equations and functions
Software Engineering
/ Iterative Design
Iterative theory refinement through mod-
elling; Model matching; Model Refine-
ment
Unit Testing and
Verification
Experimentation; Hypothesis Testing;
Verification
Formal
representations
Mathematical models and inscriptions
Perkins and Simmons (1988) argued that novice
misconceptions in math, science, and programming
exhibit similar patterns in that misunderstandings in
these domains have domain-specific (e.g., challeng-
ing concepts) and domain general (e.g., difficulties
pertaining to conducting inquiry, problem solving,
and epistemological knowledge) causes. Harel and
Papert (1991) argued that programming is reflexive
with other domains, i.e., learning programming in
concert with concepts in another domain can be eas-
ier than learning each separately. Along similar
lines, several researchers have shown that program-
ming and computational modelling can serve as ef-
fective vehicles for learning challenging science and
math concepts (Guzdial, 1995); (Sherin, 2001);
(Hambrusch et al., 2009); (Blikstein and Wilensky,
2009); (diSessa, 2000); (Kaput, 1994); (Kynigos,
2007). Table 1 illustrates components of CT that are
central to our framework and establishes their rela-
tionship to scientific practices.
2.1 Pedagogical Benefits of Integrating
CT with Science Curricula
We discuss a number of pedagogical benefits that
may be derived from integrating CT and K-12 sci-
ence curriculum units.
A. Lowering the learning threshold by reorganizing
scientific and mathematical concepts around intui-
tive computational mechanisms: Several studies
have shown that through programming, students can
construct representations of physics concepts such as
speed and acceleration, which in turn provides moti-
vation for learning programming and leads to a
deeper understanding of concepts in both domains
(Sherin, 2001); (Soloway, 1996); (Guzdial, 1995);
(diSessa, 2000); (Papert, 1980). Sherin (2001) and
diSessa (2000) argued that programming enables
novice learners to access their intuitions about the
physical world. Redish and Wilson (1993) argued
that computational representations enable us to in-
troduce discrete forms of the fundamental laws,
which can be much simpler to explain and under-
stand than the continuous forms traditionally pre-
sented in equation-based instruction. Furthermore,
these studies also suggest that in the domains of
physics and biology, rather than organizing scientific
phenomena and domains in terms of abstract
mathematical principles, these phenomena can be
organized in a more intuitive fashion around compu-
tational mechanisms and principles (Redish and
Wilson, 1993); (Sengupta and Wilensky, 2011);
(Wilensky and Reisman, 2006).
B. Programming and computational modelling as
embodiments of core scientific practices: Soloway
(1993) argued that learning to program amounts to
learning how to construct mechanisms and explana-
tions. Therefore, the ability to build computational
models by programming corresponds to core scien-
tific practices, such as model building and verifica-
tion. Lehrer, Schauble and Lucas (2008) indicate
that modelling is a fundamental component of in-
quiry in science. Regardless of the domain, scien-
tists’ work involves building and refining models of
the world (Stewart and Golubitsky, 1992).
C. Developing pre-algebra concepts through graph-
ing functions and linked representations: Much like
computational environments for science, environ-
ments like SimCalc (Kaput, 1994; Hegedus and Ka-
INTEGRATINGCOMPUTATIONALTHINKINGWITHK-12SCIENCEEDUCATION-ATheoreticalFramework
41

put, 2004) ESCOT (Roschelle et al., 1999), and E-
slate (Kynigos, 2001, 2007) enable students to learn
algebra by creating their own dynamic representa-
tions of concepts, such as rate and proportion,
through animations of actors. Based on this research,
our goal is to provide students with the following
opportunities within an integrated modelling plat-
form by (a) linking the underlying computational
model (i.e., agent-based program) with the resultant
visualization of the programmed behaviours as well
as mathematical inscriptions (e.g., graphs) to meas-
ure salient aspects of the simulated behaviours; (b)
importing physical data into the mathematical realm
in active ways, and (c) manipulating functional
forms to develop mathematical narratives and expla-
nations of scientific phenomena.
D. Contextualized representations make it easier to
learn programming: When computational mecha-
nisms are anchored in real (world) problem contexts,
programming and computational modelling become
easier to learn. Hambrusch et al. (2009) found that
introducing computer programming to undergradu-
ate non-CS major students in the context of model-
ling phenomena in their major domains (physics and
chemistry) resulted in higher learning gains (in pro-
gramming), as well as a higher level of engagement.
2.2 Agent-based Computation
In this work, we focus on multi-agent-based compu-
tational modelling (MABM). An example of a multi-
agent programming platform widely used by both
researchers and educators is NetLogo (Wilensky,
1999); (Sengupta and Wilensky, 2009). The term
“agent” in the context of MABMs denotes individual
computational objects or actors (e.g., cars), which
are controlled by simple rules assigned by the user.
It is the interactions between agents (based on these
rules) that give rise to emergent, aggregate-level be-
haviour (e.g., formation of a traffic jam – while in-
dividual cars move forward, the traffic jam moves
backward – see Resnick, 1994).
When students learn using MABMs, they use
their intuitive knowledge at the agent level as they
are asked to manipulate and reason about the behav-
iours of individual agents. Then, by visualizing and
analyzing the aggregate-level behaviours that are
dynamically displayed in MABM simulations, stu-
dents can develop multi-level explanations by con-
necting their relevant agent-level intuitions with the
emergent phenomena (Resnick, 1994); (Wilensky
and Resnick, 1999); (Klopfer et al., 2005); (Sen-
gupta and Wilensky, 2011); (Blikstein and Wilen-
sky, 2009). These scholars have argued that in most
science classrooms, aggregate-level formalisms are
typically used to teach scientific concepts and phe-
nomena, such as using the Lotka-Volterra differen-
tial equation to explain how populations of different
species in a predator-prey ecosystem evolve over
time (Wilensky and Reisman, 2006). In contrast,
when complex phenomena (e.g., microscopic proc-
esses of electrical conduction) that are traditionally
taught in college are represented in the form of
multi-agent based models, much younger students
(e.g., 4
th
and 5
th
graders) can access and understand
those phenomena (Sengupta and Wilensky, 2011);
(Dickes and Sengupta, 2011).
Among the earliest and best-known agent-based
programming languages is Logo (Papert, 1980),
which has been widely used to support children’
learning through constructionist activities (i.e.,
through the creation of personally meaningful com-
putational artifacts). The core building blocks for
constructionist (or design-based learning) activities
in Logo are computational procedures, which facili-
tate simultaneous learning of concepts about the
phenomena being modelled and computational con-
cepts, such as procedure abstraction, iteration, and
recursion.
2.3 Visual Programming
In visual programming environments, students can
construct programs using graphical and physical ob-
jects, typically using a drag-and-drop interface (Kel-
leher and Pausch, 2005); (Hundhausen and Brown,
2007). This significantly reduces students’ chal-
lenges in learning the language syntax (compared to
text-based programming), and thus makes program-
ming more accessible to novices, This is an impor-
tant affordance of visual programming, because
prior research showed that students in a LOGO pro-
gramming-based high school physics curriculum
faced significant challenges in writing programs for
modelling kinematics even after multiple weeks of
programming instruction (Sherin et al., 1992)
Some examples of visual agent-based program-
ming are AgentSheets (Reppening, 1993), StarLogo
TNG (Klopfer et al., 2005), Scratch (Maloney et al.,
2004), ToonTalk (Kahn, 1996), Stagecast Creator
(Smith et al., 2000), Kedama (Oshima, 2005) and
Alice (Conway, 1997). Common characteristics of
all these environments are: (a) users can construct or
design their programs by arranging icons or blocks
that represent programming commands and (b) these
platforms employ animations to represent the en-
actment (i.e., the execution) of the user-generated
algorithm (i.e., program), albeit with varying de-
CSEDU2012-4thInternationalConferenceonComputerSupportedEducation
42
grees of algorithm visualization (Hundhausen and
Brown, 2007).
3 SYSTEM DESIGN
FRAMEWORK
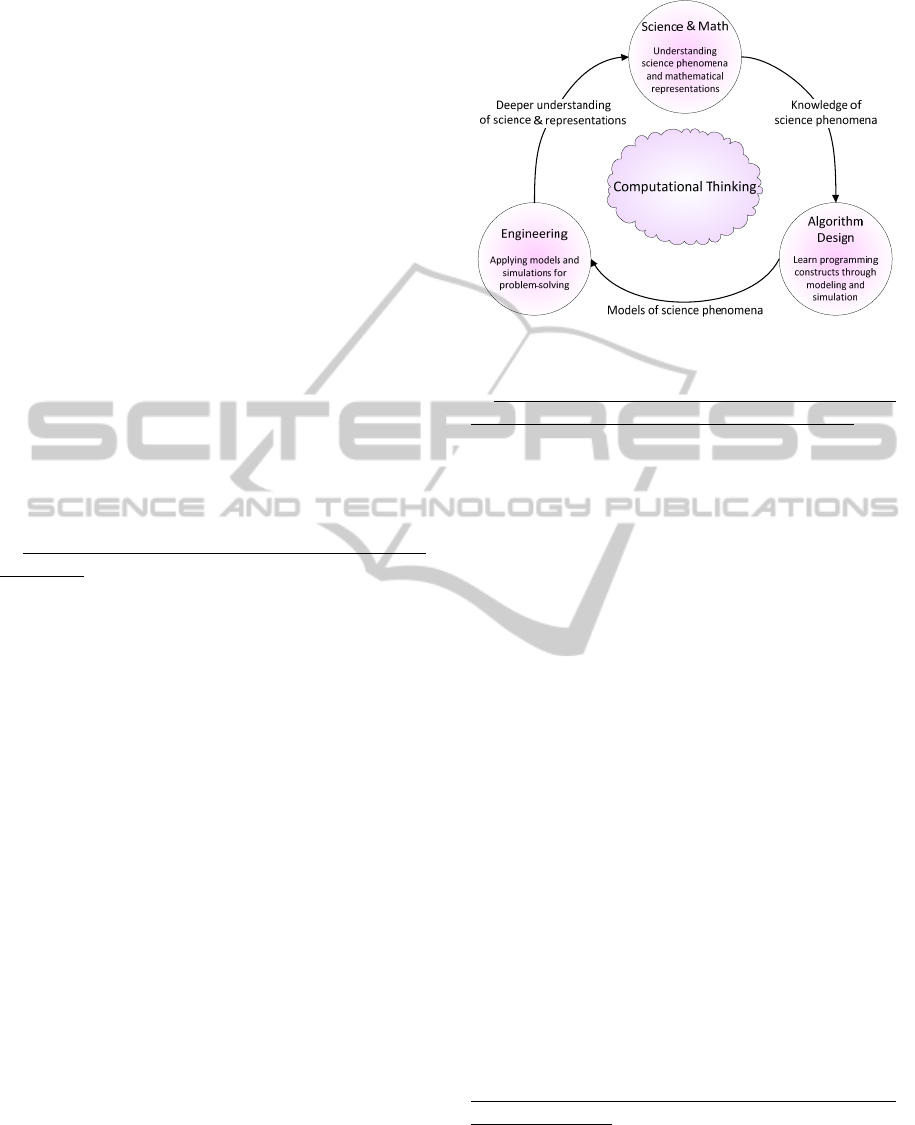
Figure 1 illustrates the conceptual framework for our
integrated approach to science learning through
computational thinking. The framework captures a
typical learning-by-design progression, which in-
cludes learning the basics of a science unit, model-
ling the entities and processes in the unit using a
visual agent-based computational framework, simu-
lating and studying the behaviour of the model, us-
ing explanation and argumentation skills to fully un-
derstand and verify the model, and finally applying
the developed model and the learned science con-
cepts to problem-solving situations.
In what follows, we outline our key design prin-
ciples, some of which has been adapted from Sen-
gupta (2011).
A. Achieving Low Threshold and High Ceiling – The
Trade-offs: For a computing medium to be widely
usable in K-12 science classrooms it must have the
following affordances: (1) it should be easy to use
for novice students; (2) learning activities should be
well-integrated with the existing science curricula;
(3) teachers, who are likely to have little or no com-
puting background, should be able to master the sys-
tem with minimal or no professional development;
and (4) while low-threshold is a definite requirement
for our system, it should not impose arbitrary ceil-
ings on the levels of complexity for modelling and
analysis by students over time. Therefore, our goal
here is to find a sweet spot that encapsulates low-
threshold (i.e., easy to program, similar to NetLogo
and Logo), wide walls (i.e., students should be able
to design a wide range of artifacts, such as anima-
tions, games, and science experiments, much like
Scratch), and high ceiling (e.g., NetLogo supports
advanced programming and modelling of complex
phenomena using a library of intuitive programming
primitives). While many of these design principles
are shared by other modelling platforms (e.g., Logo,
NetLogo, and Scratch), CTSiM is being designed
specifically for pedagogical use in science class-
rooms, keeping both teachers and students in mind
as users. This is reflected in the design of domain-
specific programming primitives, scaffolds to make
algorithms “live” and to support experimentation,
and an explicit focus on curricular integration. We
discuss these in detail in the rest of this section.,
Figure 1: CTSiM conceptual framework.
B. Incorporate Multiple “Liveness” Factors as Sup-
port for Programming and Learning by Design: Our
challenge is to design a system that lets students
seamlessly progress through cycles of construction,
execution, analysis, reflection, and refinement using
timely feedback from the simulation environment
and scaffolding provided by the system. To support
learning activities that involve rapid prototyping, our
CTSiM system will offer learners a range of “live-
ness” factors for algorithm construction, visualiza-
tion, analysis, and reflection (Tanimoto, 1990). This
primary design objective is to enable the learners to
identify the relationship between their programs
(i.e., algorithms) in the Construction World (see
Section 4.1), and the resultant enactment of their
simulations in the Enactment World (see Section
4.2). This involves developing scaffolds for support-
ing algorithm visualization (e.g., highlighting step-
by-step execution of commands; controlling the de-
lay between execution of successive commands).
The goal is to provide timely feedback to students in
order to avoid situations where lack of feedback and
scaffolding may cause errors to accumulate late into
the construction process, which makes the source of
errors harder to detect. Accumulation of errors often
leads to students being overwhelmed in terms of
their cognitive abilities, resulting in their applying
trial and error rather than systematic methods to
conduct scientific inquiry (Segedy, Kinnebrew, and
Biswas, in review).
C. Verification and Validation to Support Learning
of Expert Models: True scientific expertise involves
understanding how knowledge is generated, justi-
fied, and evaluated by scientists and how to use such
knowledge to engage in inquiry (Driver, Newton,
and Osborne, 2000; Duschl and Osborne, 2002).
Novice science learners engaging in these aspects of
INTEGRATINGCOMPUTATIONALTHINKINGWITHK-12SCIENCEEDUCATION-ATheoreticalFramework
43

inquiry often struggle without extensive scaffolding
(e.g., Klahr et al., 1990); (Schauble et al., 1991);
(Sandoval and Millwood, 2005). This is a challenge
in computational modelling environments, where
learning is often assumed to arise as students build
their models and then verify them by comparing the
behaviours generated against real data or behaviours
of reference models representing the actual phenom-
ena (Bravo et al., 2006). Therefore, building appro-
priate scaffolding and feedback is vital to the suc-
cess of such environments. In CTSiM, learners will
iteratively refine their programs by effectively com-
paring results of their simulation to an “expert” (i.e.,
canonically correct) simulation, understand the dif-
ferences, and then map elements and constructs in
their model to behaviours exhibited by their simula-
tion and vice-versa. We will extensively scaffold
this process to support experimentation and meas-
urement activities, as discussed in Section 4.3.
D. Choice of Curricular Topics
: The phenomena we
have chosen as contexts for disciplinary learning are
kinematics (physics) and ecology (biology), which
are common and important curricular topics. Re-
searchers have shown that K-12 students find these
phenomena quite challenging to understand (Chi et
al., 1994). Furthermore, it has been argued that stu-
dents’ difficulties in both the domains have similar
epistemological origins, in that both kinematic phe-
nomena (e.g., change of speed over time in an accel-
eration field) and system-level behaviours in an eco-
system (e.g., population dynamics) involve under-
standing aggregation of interactions over time
(Reiner et al., 2000); (Chi, 2005). As discussed in
Section 2.2, agent-based modelling is ideally suited
for representing such phenomena, as it enables the
learner to recruit their intuitions about agent-level
behaviours and organize them through design-based
learning activities (Kolodner et al., 2003), in order to
explain aggregate-level outcomes.
4 IMPLEMENTING CTSIM:
ARCHITECTURE AND
MODULES
The CTSiM environment will be made up of three
primary modules:
1. The Construction World: This module provides
the visual programming interface for the student to
build a computational model by composing pro-
grams. Students select primitives from a library of
commands and arrange them spatially, using a drag-
and-drop interface to generate their programs. These
programs control behaviours of individual-level
agents in a NetLogo simulation.
2. The Enactment World: This module is a mi-
croworld (Papert, 1980; White and Frederiksen,
1990) in the form of a NetLogo simulation, which
simulates the agent-level behaviours modelled by
the student in the Construction World.
3. The Envisionment World: This module works
closely with the enactment world, helping the stu-
dent to set up experiments to analyze the behaviour
of their models and to compare their model against
an expert model. Much of the scaffolding and feed-
back to help students refine, understand, and verify
their models is also provided in this module.
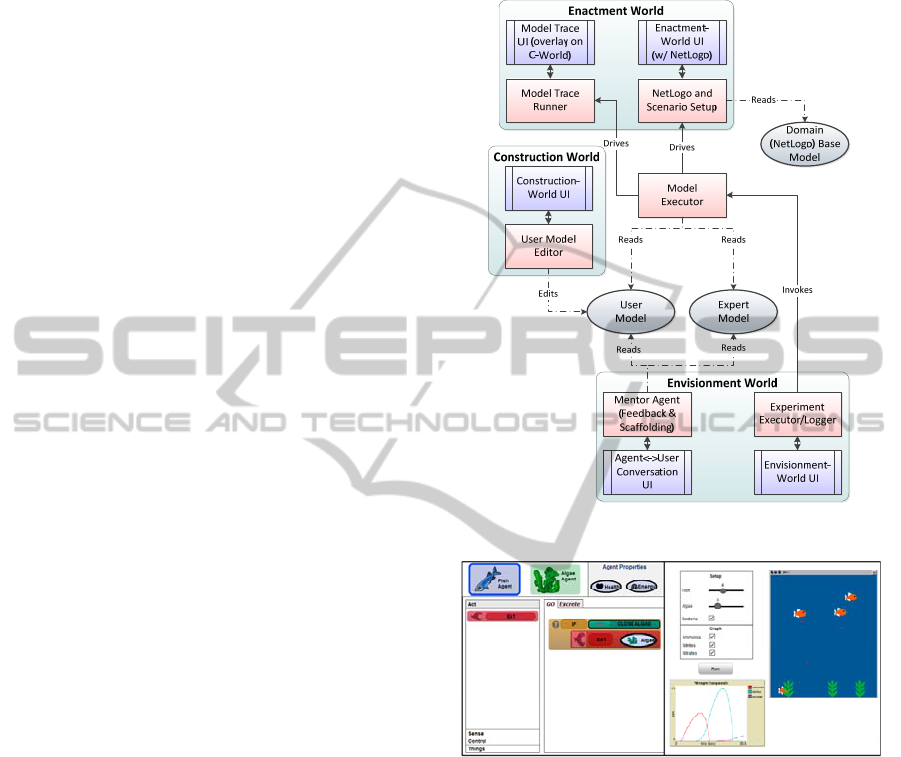
The overall system architecture is illustrated in Fig-
ure 2Error! Reference source not found.. The rest
of this section provides a brief description of the
three modules, and illustrates their functionality us-
ing a biology learning unit – a simple fish tank eco-
system that includes fish, algae, and bacteria that
break down organic waste.
4.1 Construction World
The construction world allows students to build the
relevant science model using an agent-based frame-
work with relevant computational constructs. Figure
3 presents a mock-up of the drag-and-drop model-
ling interface (illustrated on the left side of the fig-
ure) in which students define their computational
models for a simplified fish tank microworld. The
students define the model for each type of agent by
arranging and parameterizing a set of visual primi-
tives, as illustrated for a partial fish agent model in
Figure 3.
The visual primitives are named and iconically
depicted in terms of their scientific function. These
primitives are of three types: agent actions in the mi-
croworld (e.g., movement, eating, reproducing),
sensing (e.g., vision, colour, touch, toxicity), and
controlling the flow of execution in the computa-
tional model (e.g., conditionals, loops). Each visual
primitive, in turn, is defined in terms of an underly-
ing computational primitive (with appropriate con-
straints and parameters), as illustrated in Figure 4.
The computational primitives provide a domain-
independent set of computational constructs in a va-
riety of categories: 1) changing (e.g., increasing or
decreasing) a property of the agent, 2) sensing con-
ditions of the agent or its environment (e.g., reading
local or global variable values), 3) creating or de-
stroying agents (e.g., to model birth and death), and
4) conditionals and logical operators for controlling
execution flow.
CSEDU2012-4thInternationalConferenceonComputerSupportedEducation
44
4.2 Enactment World
The enactment world interface allows the student to
define a scenario (as a set of initial parameters) and
visualize the multi-agent-based simulation driven by
their model. The CTSiM environment, implemented
in Java, includes an embedded instance of NetLogo
to implement the visualization and mechanics of the
simulation. As the student builds a model, it is repre-
sented in the system as a code graph of parameter-
ized computational primitives, illustrated in Figure
4. This code graph remains hidden from the end-user
(the learner), who accesses the environment using
the UI as shown in Figures 3 and 5. The code graph
enables the system to simulate the user-generated
model for a given scenario by stepping through the
graph and executing the computational primitives.
The execution of the computational primitives indi-
cated by the current (user) model drives the NetLogo
simulation, as illustrated in Figure 2. NetLogo visu-
alization and plotting/measurement functionality (il-
lustrated in Figure 4) provide the students with a dy-
namic, real-time display of how their agents operate
in the microworld, thus making explicit the emer-
gence of aggregate system behaviours (e.g., from
graphs of the population of a species over time).
Furthermore, since there is a one-to-one corre-
spondence between the visual primitives in the con-
struction world model and the computational primi-
tives in the execution model (code graph), the sys-
tem can highlight each primitive in the construction
world as it is executed in the enactment world. This
model-tracing functionality will be leveraged to pro-
vide important scaffolding that supports model re-
finement and debugging activities.
5 ENVISIONMENT WORLD
The envisionment world provides students with a
space where they can systematically design experi-
ments to test their constructed models and compare
their model behaviours against behaviours generated
by an “expert” model. A typical experimental setup
would involve assigning values to agent parameters
and variables defined in the student model, and si-
multaneously simulating the expert model with the
same parameter values. Although the expert model
is hidden, students may observe its behaviour in
comparison to their own model with side-by-side
plots and microworld visualizations. With additional
scaffolding and support, this allows students to make
decisions on what components of their models they
need to investigate, develop further, or check for er-
rors to correct. Figure 5 illustrates a mock-up of the
envisionment world window that we are designing
from CTSiM.
Figure 2: CTSiM architecture.
Figure 3: Construction- and enactment-worlds interface
mock-up.
Work by Basu, Sengupta, and Biswas (in review)
details our approach to simulation investigation and
discusses the scaffolds that we have developed to
help students study and understand underlying
model concepts and relations in a desert ecosystem
microworld. With proper support and scaffolding,
we believe that the overall process of model con-
struction, analysis, comparison, and refinement will
help students gain a better understanding of science
(e.g., science phenomena and the scientific reason-
ing process), mathematics (e.g., measurement,
graphs, and equations), and computational constructs
and methods.
INTEGRATINGCOMPUTATIONALTHINKINGWITHK-12SCIENCEEDUCATION-ATheoreticalFramework
45

Figure 4: Construction-world and execution models.
To further support learning science by model
building, analysis, and verification, we plan to de-
velop a module for critique, explanation, and argu-
mentation that will engage students in authentic
analysis and inquiry practices. For example, each
cycle of modelling will begin with students critiqu-
ing the fit between the current version of their
model, and the target agent- and aggregate-level be-
haviours generated from the expert model. If differ-
ences in system behaviour (between the expert
model and the student’s model) are identified
through the critique phase, the student will then be
scaffolded in creating an explanation/claim about the
mechanisms in their constructed model that could
lead to the observed differences. The methods dis-
cussed in the construction and enactment worlds will
support this interaction and help students identify the
segments of their model that are contributing to dif-
ferences in system behaviour. The goal is to scaffold
explanation about the underlying causal mechanism
that simultaneously identifies an issue and proposes
corrective action.
After creating an explanation about the source of
differences between the agent-level program and ag-
gregate-level outputs, the student will be scaffolded
to identify and collect further evidence for, or
against, the proposed causal mechanism. This can
include evidence collected during the critiquing
phase or during subsequent experimentation. Re-
search has shown that students initially tend to focus
only on evidence that supports their claims and ig-
nore the evidence that contradicts their claims, in a
manner very similar to the ways in which scientists
have historically dealt with anomalous data (Chinn
and Brewer, 1993). Therefore, the scaffolding
should help students search for evidence that might
contradict their claims, as well as evidence that sup-
ports their claims.
Figure 5: Envisionment world interface mock-up.
6 SEQUENCE OF CURRICULAR
MODULES AND ACTIVITIES
We are currently developing two curricular models
in the CTSiM environment: (1) a kinematics unit
that focuses on modelling Newtonian mechanical
phenomena such as the trajectory, velocity, and ac-
celeration of balls placed on different inclined
planes, as well as using mathematically meaningful
aesthetic representations (e.g., geometric shapes) to
represent various classes of kinematic phenomena
(e.g., constant speed, constant acceleration) (Sen-
gupta, 2011); (Sengupta, Voss Farris, and Wright,
under review); and (2) an ecological unit (Tan and
Biswas, 2007) that emulates a simplified fish tank
environment, which includes fish, algae, and bacte-
ria for breaking down organic waste; it primarily
models a simplified food chain and the waste cycle
focusing on how organic waste is broken down in
steps by bacteria to produce nitrates, which provide
nutrition for algae. The focus of this unit is on the
study of interdependence and balance in ecosystems.
In terms of learning programming, these model-
ling activities will introduce students to fundamental
programming constructs (e.g., agents, conditionals,
loops, variables, etc.). For example, the first two
modelling tasks in both kinematics and ecology in-
volve students using three main types of constructs:
CSEDU2012-4thInternationalConferenceonComputerSupportedEducation
46

agents (various species of organisms in ecology;
physical objects in kinematics), conditionals (indi-
cating need-based interactions between agents in
ecology, and effect of different conditions, e.g., ter-
rains, in kinematics), and loops (for repetitions of an
action(s) based on the current value of an agent’s or
environmental property/variable). In subsequent
modelling activities, students will learn to define
variables (e.g., defining attributes of agents and
breeds of agents), as well as code-reuse and encap-
sulation (e.g., using portions of existing code to
model behaviour of new agents). In later, more
complex, modules, students will explore class hier-
archy/inheritance connected to science through rela-
tion to taxonomy and class/type properties and be-
haviours, as well as the nature of physical “laws”
that apply to all objects (e.g., in kinematics).
From the mathematical perspective, students in
both curricular units will focus on: (1) generating
graphs of aggregations (e.g., averages) over time, (2)
identifying and developing basic mathematical rela-
tionships between variables and statistical properties
of populations evident from graphs (e.g., linear vs.
quadratic relationships, averages, range, vari-
ance/standard-deviation), and (3) understanding
rates through designing multiple, linked representa-
tions of rates and other time-based/time-variant rela-
tionships. For example, students would start out
visualizing a variable’s value changing over time, ei-
ther step-by-step or plotted on a graph, and then
learn to represent it as a simple equation.
7 DISCUSSION AND
CONCLUSIONS
In general, computational thinking involves being
able to reason at multiple levels of abstraction
(Kramer, 2007), mathematical and design-based
thinking (Wing, 2008), as well as using these kinds
of reasoning for contextual problem solving (Guz-
dial, 2008); (Wing, 2008). Our paper proposes a
theoretical framework through which these aspects
of CT can be integrated with curricular modules in
K-12 science classrooms via agent-based modelling.
We also presented the computational architecture of
a learning environment based on this theoretical
framework that includes a visual programming lan-
guage and a modelling environment. In designing
this system, our goal is to integrate computational
thinking with existing K-12 science curricula (as has
been recommended by the ACM K-12 Taskforce
(2003)), without necessitating the development of
new curricular standards or introducing a program-
ming course separately from the curricular science.
This also lays the groundwork for the development
of a long-term curricular progression in which stu-
dents can engage in learning science using computa-
tional modelling and thinking over a span of multi-
ple years. This is consistent with the findings from
research in developmental psychology and science
education, which show that the development of sci-
entific thinking, even when it builds on students’ in-
tuitive knowledge and competencies, happens over a
period of multiple years through meaningful immer-
sion in authentic learning experiences (Lehrer et al.,
2008).
By engaging students in agent-based modelling
across multiple domains, but using the same pro-
gramming constructs and modelling environment,
our primary goal is to enable students to realize the
commonalities across domains in terms of the under-
lying computational/mathematical constructs and
practices (e.g., control flow, variables, debugging),
as well as the domain-general representational prac-
tices involved in modelling (e.g., problematizing,
experimentation, generating inscriptions, verifica-
tion, and validation). We will run classroom studies
with the first prototype of our system in Spring
2012, to study some of these claims and to collect
data for refining and continuing the development of
CTSiM.
ACKNOWLEDGEMENTS
Thanks to Satabdi Basu, Amanda Dickes, Brian Sul-
cer, Jaymes Winger, and Mason Wright (in no par-
ticular order). This work is partially supported by
NSF IIS # 1124175.
REFERENCES
ACM K-12 Taskforce (2003). A Model Curriculum for K-
12 Computer Science: Final Report of the ACM K-12
Task Force Curriculum Committee, CSTA, New York,
NY.
Basu, S., Sengupta, P. and Biswas, G., (In Review). A
scaffolding framework to support learning in multi-
agent based simulation environments. Computers and
Education.
Baumgartner, E. and Reiser, B. J., (1998). Strategies for
supporting student inquiry in design tasks. Annual
Conference of the American Educational Research As-
sociation, San Diego, CA, April 13, 1998.
Blikstein P. and Wilensky, U., (2009). An Atom is Known
by the Company it Keeps: A Constructionist Learning
INTEGRATINGCOMPUTATIONALTHINKINGWITHK-12SCIENCEEDUCATION-ATheoreticalFramework
47

Environment for Materials Science Using Agent-
Based Modeling. Int J Comput Math Learning, 14:81–
119.
Bravo, C., van Joolingen, W. R., and deJong, T., (2006).
Modeling and Simulation in Inquiry Learning: Check-
ing Solutions and Giving Advice. Simulation, 82(11),
769-784.
Chi, M. T. H., (2005). Common sense conceptions of
emergent processes: Why some misconceptions are
robust. Journal of the Learning Sciences, 14: 161-199.
Chi, M. T. H., Slotta, J. D. and de Leeuw, N., (1994).
From things to processes: A theory of conceptual
change for learning science concepts. Learning and
Instruction, 4: 27-43.
Chinn, C. A., and Brewer, W. F., (1993). The role of
anomalous data in knowledge acquisition: A theoreti-
cal framework and implications for science instruc-
tion. Review of Educational Research, 63, 1–49.
Conway, M., (1997). Alice: Easy to Learn 3D Scripting
for Novices, Technical Report, School of Engineering
and Applied Sciences, University of Virginia, Char-
lottesville, VA.
diSessa, A. A., (1986). BOXER: A Reconstructible Com-
putational Medium. Communications of ACM, 29(9):
859-868.
diSessa, A. A., (2000). Changing Minds: Computers,
Learning, and Literacy. Cambridge, MA: MIT Press.
Dickes, A., and Sengupta, P., (2011). Learning Natural
Selection in 4th Grade With Multi-Agent-Based Com-
putational Models. In Sengupta, P. (Chair), and Hall,
R. (Discussant). Models, Modeling, and Naïve Intui-
tive Knowledge in Science Learning. Symposium pre-
sented at the 41st Annual Meeting of the Jean Piaget
Society, Berkeley, CA.
Driver, R., Newton, P., and Osborne, J., (2000). Establish-
ing the norms of scientific argumentation in class-
rooms. Science Education, 84(3), 287-313.
Duschl, R. A., and Osborne, J., (2002). Supporting and
promoting argumentation discourse in science educa-
tion. Studies in Science Education, 38, 39-72.
Guzdial M., (1995) Software-realized scaffolding to facili-
tate programming for science learning. Interactive
Learning Environments, 4(1). 1-44.
Guzdial, M., 2008. “Paving the way for computational
thinking.” Education Column. Communications of the
ACM, 51(8)
Hambrusch, S., Hoffmann, C., Korb, J. T., Haugan, M.,
and Hosking, A. L., (2009). A multidisciplinary ap-
proach towards computational thinking for science
majors. In Proceedings of the 40th ACM technical
symposium on Computer science education (SIGCSE
'09). ACM, New York, NY, USA, 183-187.
Harel, I. and Papert, S., (1991). "Software design as a
learning environment". Constructionism. Norwood,
NJ: Ablex Publishing Corporation. pp. 51–52. ISBN
0-89391-785-0.
Hegedus, S. J. and Kaput, J. J., (2004). An Introduction to
the Profound Potential of Connected Algebra Activi-
ties: Issues of Representation, Engagement, and Peda-
gogy, Proceedings of the 28th Conference of the In-
ternational Group for the Psychology of Mathematics
Education
, 3, 129–136.
Hundhausen, C. D., Brown, J. L., (2007). What You See Is
What You Code: A “live” algorithm development and
visualization environment for novice learners. Journal
of Visual Languages and Computing, 18: 22-47.
Kafai, Y., and Soloway, E., (1994). Computational Gifts
for the Barney Generation. Commun. ACM, 37(9): 19-
22.
Kahn, K., (1996). ToonTalk: An Animated Programming
Environment for Children, Journal of Visual Lan-
guages and Computing.
Kaput, J., (1994). Democratizing access to calculus: New
routes using old routes. In Schoenfeld, A. (ed.), Ma-
thematical Thinking and Problem Solving, Lawrence
Erlbaum, Hillsdale, NJ, 77-156.
Kelleher, C. and Pausch, R., (2005) Lowering the barriers
to programming: a taxonomy of programming envi-
ronments and languages for novice programmers,
ACM Computing Surveys, Vol. (37) 83–137.
Klahr, D., Dunbar, K., and Fay, A. L., (1990). Designing
good experiments to test bad hypotheses. In J. Shrager
and P. Langley (Eds.), Computational models of scien-
tific discovery and theory formation (pp. 355-401).
San Mateo, CA: Morgan Kaufman.
Klopfer, E., Yoon, S. and Um, T., (2005). Teaching Com-
plex Dynamic Systems to Young Students with Star-
Logo. The Journal of Computers in Mathematics and
Science Teaching; 24(2): 157-178.
Kolodner, J. L., Camp, P. J., Crismond, D., Fasse, B.,
Gray, J., Holbrook, J., Puntambekar, S., and Ryan, M.,
(2003). Problem-Based Learning meets Case-Based
Reasoning in the Middle-School Science Classroom:
Putting Learning by Design into Practice. The Journal
of Learning Sciences, 12(4) 495-547.
Krajcik, J., McNeill, K. L. and Reiser, B., (2008). Learn-
ing-goals-driven design model: Curriculum materials
that align with national standards and incorporate
project-based pedagogy. Science Education, 92(1), 1-
32.
Kramer, J., (2007). Is abstraction the key to computing?
Commun. ACM 50, 4 (April 2007), 36-42.
Kynigos, C., (2007). Using half-baked microworlds to
challenge teacher educators’ knowing, Journal of
Computers for Math Learning, 12(2), 87-111.
Kynigos, C., (2001). E-slate Logo as a basis for construct-
ing microworlds with mathematics teach-
ers. Proceedings of the Ninth Eurologo Conference,
Lintz, Austria, 65-74.
Lehrer and Romberg (1996). Exploring Children’s Data
Modeling, Cognition and Instruction, 14(1): 69-108.
Lehrer, R., Schauble, L., and Lucas, D., (2008). Support-
ing development of the epistemology of inquiry. Cog-
nitive Development, 23 (4), 512-529.
Maloney, J., Burd, L., Kafai, Y., Rusk, N., Silverman, B.,
and Resnick, M., (2004) Scratch: A Sneak Preview. In
Proc. of Creating, Connecting, and Collaborating
through Computing,
104-109.
NRC (2010). Report of a Workshop on The Scope and Na-
ture of Computational Thinking.
CSEDU2012-4thInternationalConferenceonComputerSupportedEducation
48

Oshima, Y., (2005). Kedama: A GUI-based Interactive
Massively Parallel Particle Programming System.
Proceedings of the 2005 IEEE Symposium on Visual
Languages and Human-Centric Computing
(VL/HCC’05).
Papert, S., (1980). Mindstorms: children, computers, and
powerful ideas. Basic Books, Inc. New York, NY.
Papert, S., (1991). Situating constructionism. In I. Harel
and S. Papert (Eds.), Constructionism. Norwood, NJ:
Ablex Publishing Corporation.
Pea, R. D., (1986). Language-independent conceptual
bugs in novice programming. Journal of Educational
Computing Research, 2(1), 25-36.
Perkins, D. N., (1986). Knowledge as design. Hillsdale, N.
J.: Lawrence Erlbaum Associates.
Perkins, D. N. and Simmons, R., (1988). Patterns of mi-
sunderstanding: An integrative model for science,
math, and programming. Review of Educational Re-
search, 58(3), 303-326.
Redish, E. F. and Wilson, J. M., (1993). Student pro-
gramming in the introductory physics course:
M.U.P.P.E.T. Am. J. Phys. 61: 222–232.
Reiner, M., Slotta, J. D., Chi, M. T. H., and Resnick, L. B.,
(2000). Naive physics reasoning: A commitment to
substance-based conceptions. Cognition and Instruc-
tion, 18(1), 1-34.
Repenning, A., (1993). Agentsheets: A tool for building
domain-oriented visual programming, Conference on
Human Factors in Computing Systems, 142-143.
Resnick, M., (1994). Turtles, Termites, and Traffic Jams:
Explorations in Massively Parallel Microworlds.
Cambridge, MA: MIT Press.
Roschelle, J., Digiano, C., Pea, R. D. and Kaput, J.,
(1999). Educational Software Components of Tomor-
row (ESCOT), Proceedings of the International Con-
ference on Mathematics/Science Education and Tech-
nology (M/SET), March 1-4, 1999. San Antonio, USA.
Sandoval, W. A., and Millwood, K., (2005). The quality of
students' use of evidence in written scientific explana-
tions. Cognition and Instruction, 23(1), 23-55.
Schauble, L., Klopfer, L. E., and Raghavan, K., (1991).
Students' transition from an engineering model to a
science model of experimentation. Journal of Re-
search in Science teaching, 28, 859-882.
Segedy, J. R., Kinnebrew, J. S., and Biswas, G., (In Re-
view). Promoting Metacognitive Learning Behaviors
using Conversational Agents in a Learning by Teach-
ing Environment, Educational Technology Research
and Development.
Sengupta, P., (2011). Design Principles for a Visual Pro-
gramming Language to Integrate Agent-based model-
ing in K-12 Science. In: Proceedings of the Eighth In-
ternational Conference of Complex Systems (ICCS
2011), pp 1636 - 1637.
Sengupta, P., Voss Farris, A., and Wright, M., (In Re-
view). From Agents to Aggregation via Aesthetics:
Learning Mechanics with Visual Agent-based Compu-
tational Modeling. Technology, Knowledge and Learn-
ing.
Sengupta, P. and Wilensky, U., (2011). Lowering the
Learning Threshold: Multi-agent-Based Models and
Learning Electricity. In Khine, M.S., and Saleh, I.M
(Eds.). Dynamic Modeling: Cognitive Tool for Scien-
tific Inquiry, pp 141 - 171. Springer, New York, NY.
Sherin, B., (2000). How students invent representations of
motion: A genetic account.
Journal of Mathematical
Behavior, 19(4), 399-441.
Sherin, B., (2001). A comparison of programming lan-
guages and algebraic notation as expressive languages
for physics. International Journal of Computers for
Mathematics Learning: 6, 1-61.
Smith, D., Cypher, A., and Tesler, L., (2000). Program-
ming by example: novice programming comes of age.
Communications of the ACM, 43(3), 75-81.
Soloway, E., (1993). Should We Teach Students to Pro-
gram? Commun. ACM 36(10): 21-24
Stewart, I. and Golubitsky, M. (1992). Fearful Symmetry:
Is God a Geometer?, Blackwell Publishers, Oxford.
Tan, J., and Biswas, G., (2007). Simulation-based game
learning environments: Building and sustaining a fish
tank. In Proceedings of the First IEEE International
Workshop on Digital Game and Intelligent Toy En-
hanced Learning (pp. 73-80). Jhongli, Taiwan.
Tanimoto, S. L., (1990) VIVA: a visual language for im-
age processing. Journal of Visual Languages and
Computing. 1, 127–139.
White, B. Y., and Frederiksen, J. R., (1990). Causal model
progressions as a foundation for intelligent learning
environments. Artificial Intelligence, 42(1):99-157.
Wilensky, U., (1999). NetLogo. Center for Connected
Learning and Computer-Based Modeling
(http://ccl.northwestern.edu/netlogo). Northwestern
University, Evanston, IL.
Wilensky, U., and Resnick, M., (1999). Thinking in Le-
vels: A Dynamic Systems Perspective to Making
Sense of the World. Journal of Science Education and
Technology, 8(1).
Wilensky, U., and Reisman, K., (2006). Thinking like a
wolf, a sheep or a firefly: Learning biology through
constructing and testing computational theories - An
embodied modeling approach. Cognition and Instruc-
tion, 24(2), 171-209.
Wing, J. M., (2006) Computational Thinking CACM,
Viewpoint, vol. 49, no.3 March 2006, pp. 33-35.
Wing, J. M., (2008). Computational thinking and thinking
about computing. Philosophical Transactions of the
Royal Society, vol. 366, pp.
INTEGRATINGCOMPUTATIONALTHINKINGWITHK-12SCIENCEEDUCATION-ATheoreticalFramework
49
