
SPREADING EXPERTISE SCORES IN OVERLAY LEARNER
MODELS
Martin Hochmeister
Electronic Commerce Group, Vienna University of Technology, Favoritenstraße 9-11/188-4, 1040 Vienna, Austria
Keywords:
Learner Model, Expertise, Ontology, Spreading Activation, Intelligent Tutoring Systems.
Abstract:
Intelligent tutoring systems adapt learning resources depending on learners’ models. Successful adaptation is
largely based on comprehensive and accurate learner models. By exploiting the network structure of ontology
overlay models, we infer new learner knowledge and calculate the knowledge level we refer to as expertise
scores. This paper presents a novel score propagation algorithm using constrained spreading activation and
heuristics based on relative depth scaling. The algorithm spreads expertise scores amongst topics in a learner’s
overlay model. We compared this novel approach with a baseline algorithm in the domain of programming
languages and asked human experts to evaluate the calculated scores. Our results suggest that the novel
algorithm tends to calculate more accurate expertise scores than the baseline approach.
1 INTRODUCTION
Intelligent tutoring systems recommend learning re-
sources to learners based on their learner models.
Learning resources include learning content, learn-
ing paths that may help navigating through appro-
priate learning resources or relevant peer-learners,
with whom collaborative learning may take place
(Manouselis et al., 2011). Intelligent tutoring systems
perform poorly until they collect sufficient informa-
tion about learners. Such systems may improve their
service by exploiting more comprehensive and accu-
rate learner models.
Learners’ expertise is a frequently modeled at-
tribute and if scaled quantitatively, it usually ranges
from 0 to 100 points. The dominant representation
form for modeling expertise is the ontology overlay
model (Brusilovsky and Mill´an, 2007). In this sense,
the overlay is a structural model representing learners
expertise as a subset of topics of a domain ontology.
(Kay and Lum, 2005b) suggest the use of lightweight
ontologies in favor of saving expert resources to build
relatively complete ontologies. They further conclude
that simpler inference algorithms sufficefor reasoning
about topics in the area of adaptive educational sys-
tems. Such reasoning algorithms fight sparsity and in-
crease the precision of user models. Additionally, the
trend to make user models scrutable for users (Bull
and Kay, 2010) opens another application field for
such algorithms.
In this paper, we propose an algorithm using
spreading activation to propagate expertise scores in
an overlay learner model. We address the following
research question:
Based on a learner’s expertise in topic X, how
much does the learner know about topic Y?
Spreading activation is a technique to process net-
worked data like topics in an ontology. The idea is to
transfer information between topics in the network.
In this paper, we spread learners’ expertise scores
through the network structure of a domain ontology.
The novel aspects of our algorithm are:
1. Coefficient α is used to alter a topic’s while being
activated. Thus, it ensures the alignment between
a topic and its subtopics.
2. We introduce relative depth scaling for calculat-
ing relation weights representing the similarity
between topics. These weights are used for prop-
agation, for pre-adjusting activation and for com-
paring calculated scores with the expert standard.
We compared our novel method with a baseline
approach from literature. Based on scenarios in the
domain of programming languages, we propagated
scores with both the novel and the baseline approach.
We then showed the calculated scores (novel vs. base-
line) to 29 experts for evaluation. Experts were asked
to vote for scores that seem more accurate than oth-
ers. Our results show that for some scenarios both
algorithms calculate almost equal scores. However,
175
Hochmeister M..
SPREADING EXPERTISE SCORES IN OVERLAY LEARNER MODELS.
DOI: 10.5220/0003918901750180
In Proceedings of the 4th International Conference on Computer Supported Education (CSEDU-2012), pages 175-180
ISBN: 978-989-8565-06-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

for the rest of scenarios the novel approach performs
significantly better than the baseline approach.
This paper is organized as follows. Section 2
surveys literature on overlay models as well as ap-
plications using spreading activation. Section 3 de-
scribes the details of both the baseline and the novel
approach. The evaluation and results are presented in
Section 4. We conclude in Section 5.
2 RELATED WORK
Overlay modeling has its roots in the design of a tutor-
ing system presented by (Carr and Goldstein, 1977).
They refer to a set of hypotheses as overlay that esti-
mates the confidence that a learner possesses certain
skills. The basic idea of overlays was transferred to
ontology-based user models. In this type of models,
learners’ expertise is modeled as a subset of topics
from a domain ontology representing the expert stan-
dard. The underlying network structure of the domain
ontology allows for reasoning over the topics in learn-
ers’ models. Today, this kind of user models consti-
tutes the dominant representation of users in adaptive
educational systems (Brusilovsky and Mill´an, 2007).
Spreading activation is a technique to process net-
worked data such as an ontology. It was first intro-
duced in the field of psychology (Anderson, 1983).
Computer sciences adopted spreading activation in
various areas, for instance, in information retrieval
(Crestani, 1997). Basically, spreading activation ac-
tivates topics in an ontology and passes the level of
these topics to adjacent topics as shown in Equation
1, where the level depends also on the link connecting
two topics.
I
j
=
∑
i
O
i
· ω
ij
. (1)
where I
j
represents the activation level of topic j re-
ceived from topic i depending on the relation weight
ω
ij
. Various approaches exist to determine relation
weights (Pirr`o, 2009). However, one simple way to
configure relation weights is the use of a decay factor,
which consistently attenuates the activation level dur-
ing spreading activation (Liu and Maes, 2005) (Can-
tador et al., 2008).
Spreading continues until all topics in the network
are activated. In fact, this is the main drawback of
pure spreading activation. Introducing rules adjusting
spreading activation helps to gain control of this unde-
sired behavior. Constrained spreading activation con-
siders such rules (constraints) that limit the number
of activations in the network. These rules include dis-
tance constraints, fan-out constraints, path constraints
and activation constraints (Crestani, 1997).
One of the most cited and pioneering systems
using spreading activation is GRANT (Cohen and
Kjeldsen, 1987). This system relies on an ontology
representing research topics. It activates topics ob-
tained from research proposals and spreads activation
through the ontology until funding agencies, linked to
the ontology’s topics, are activated as well. Thereby,
activation is restricted to prevent activation of possi-
bly irrelevant funding bodies.
(Liu et al., 2005) adopt spreading activation for
the purpose of ontology extension. They first aug-
ment a seed ontology with terms obtained from a col-
lection of news media sites. The relation weights are
set depending on the type of relation between terms
found in the web documents. Finally, spreading ac-
tivation yields the most promising terms, which are
then suggested to experts as candidates for ontology
extension.
(Sieg et al., 2007) utilize spreading activation to
propagate interests in a hierarchically structured user
model. They determine relation weights by a measure
of containment. Ontology topics are associated with
documents. The more equal the document term vec-
tors of topics, the higher the relation weight. A similar
approach using a hierarchy is proposed by (Schickel-
Zuber and Faltings, 2007). The amount of scores
propagated to a parent topic depends on the features
shared by the parent and the descendants in its sub-
tree.
(Kay and Lum, 2005a) apply spreading activation
to propagate a user’s expertise scores in an overlay
user model. They define the relation weight of a par-
ent topic as the reciprocal value of the total amount
of its children. To our knowledge, this is the only
directly related work to our approach as it is related
to a similar context, i.e., spreading expertise scores
of learners. Therefore, we took this approach as the
baseline for evaluation.
3 EXPERTISE SCORE
PROPAGATION
A lot of research work has been done on hierarchical
ontologies. This is not surprising since most ontolo-
gies are made of is-a relationships (Schickel-Zuber
and Faltings, 2007). Many adaptive systems claim to
utilize ontologies. In fact, they use taxonomies that
can be considered as lightweight ontologies based on
relations like is-a, part-of or similarity (Brusilovsky
and Mill´an, 2007). Figure 1 depicts a simple ontology
modeling programming languages and programming
paradigms. We built this ontology by hand based on
descriptions from Wikipedia. The links represent the
CSEDU2012-4thInternationalConferenceonComputerSupportedEducation
176
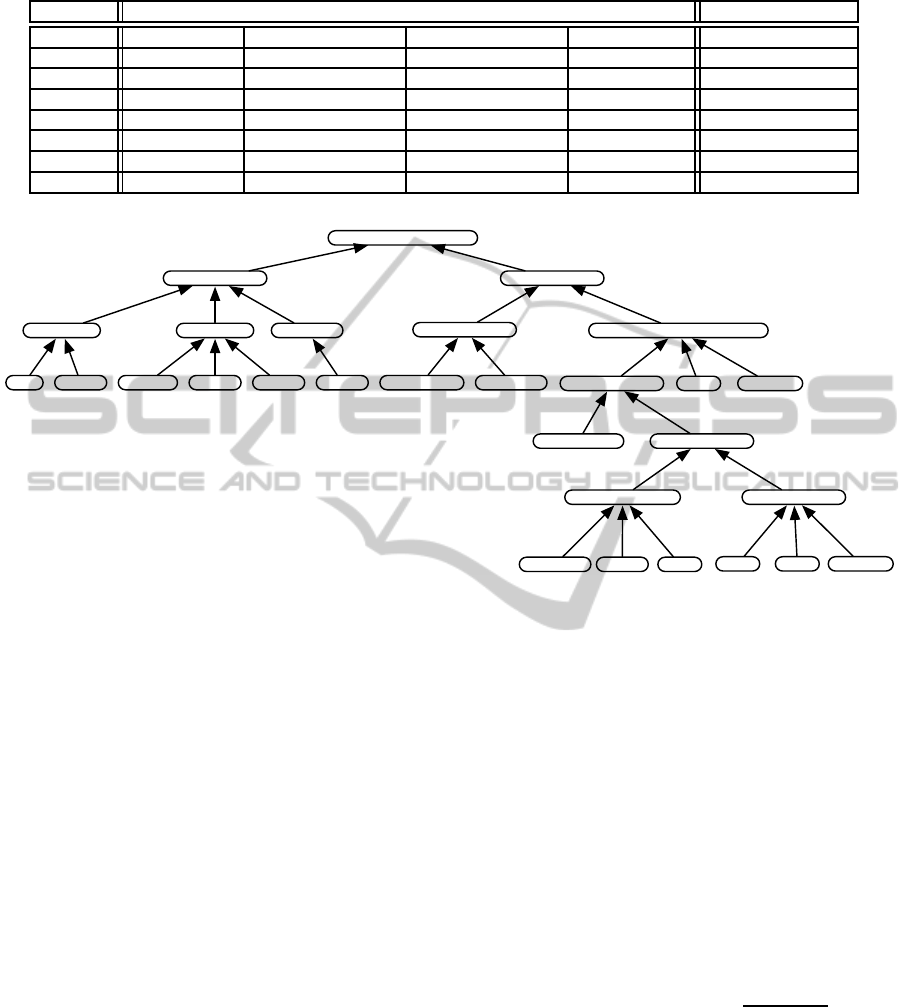
Table 1: Test scenarios.
Scenario Initial Scores (points) Topics to Estimate
1 Java: 80 C++: 30 - - object-oriented
2 Prolog: 50 COBOL: 90 object-oriented: 20 - programming
3 Smalltalk: 30 object-oriented: 50 - - structured
4 LISP: 10 Erlang: 60 Prolog: 30 - declarative
5 C++: 70 Java: 40 Falcon: 30 JavaScript: 80 object-oriented
6 Java: 90 C++: 60 Visual Basic: 30 - object-based
7 Smalltalk: 60 class-based: 30 - - class-based
8 Prolog: 40 logic: 70 - - logic
0.50.5
0.5 0.5
0.47
0.470.47
0.73
0.640.670.67
0.64
0.64
0.67
0.67 0.64
0.64
0.64
0.75
0.75
0.80.8
0.82 0.82
0.82
0.82
0.82
0.82
programming languages
object-oriented
C++
class-based
Java Smalltalk
Falcon
prototype-based
JavaScript Slate
logicfunctional
unstructured
imperativedeclarative
object-based
Visual Basic
LISP
structured
Haskell Erlang Prolog
PascalC
COBOLAssembler
constraint
Oz Turtle
Figure 1: A domain ontology modeling topics and their similarities.
similarities of topics ranging from 0 to 1. All scores
calculated in this paper are based on this ontology.
Spreading activation is made of a sequence of it-
erations (Crestani, 1997). One iteration follows the
other until a certain termination condition occurs.
Each iteration is made of one or more pulses, where
a pulse represents the process of spreading activation
from one single topic to another. A pulse consists of a
pre-adjustment and post-adjustment phase, which al-
low to attenuate previous pulses and control activa-
tion. We apply spreading activation in a hierarchical
ontology. This implies that activation is only allowed
on the shortest path leading to the root topic. An iter-
ation consists of pulses that propagate activation start-
ing from lower hierarchy levels upwards. Before any
activation starts, initially activated topics (see Table
1) will be sorted in descending order by their hier-
archy levels. Topics not being activated will receive
the activation level 0. The first iteration starts with
propagating expertise scores on the lowest level. This
process terminates at the root level.
In case a topic about being activated has already
an activation level greater than 0 (this happens when
initial activation concerns topics on different hierar-
chy levels), we perform pre-adjustment to prevent
possible distortion of activation levels. For instance,
in scenario 3 the topic object-oriented has an initial
score and will also be activated by topic Smalltalk.
3.1 Baseline Approach
(Kay and Lum, 2005a) propose an algorithm to in-
fer the scores of higher level topics from topics on
lower levels where direct evidence is available. We
set their approach as the baseline for our work since
the idea and the domain of this approach is directly
related to the algorithm presented in this paper. Equa-
tion 2 describes their approach propagating expertise
from topics in C
p
to an adjacent topic p located one
hierarchy level above.
S(p) = S(p) + (1− S(p)) ·
∑
c∈C
p
S(c)
|C
p
|
. (2)
where C
p
is the set of topic p’s children.
3.2 Novel Approach
We propose an algorithm based on constrained
spreading activation. By means of relative depth
scaling as introduced by (Sussna, 1993), we assign
weights to the ontology’s relations. Equation 3 shows
SPREADINGEXPERTISESCORESINOVERLAYLEARNERMODELS
177

activation, where topic p is activated by topic c. The
overall score S(p) is the sum of scores received from
activated subtopics. Scores are propagated level by
level starting with the lowest activated topics up to
the root.
S(p) = α· S(p) +
∑
c∈C
p
S(c) · ω
Sussna(p,c)
n
ExpertStandard
(p)
· γ . (3)
where α is a coefficient for generalization and
ω
Sussna(p,c)
the weight of the link connecting topic p
and c. The decay factor γ controls the intensity of ac-
tivation. In the following, we describe each term in
Equation 3 in detail.
3.2.1 Relation Weights
A relation linking two topics represents their similar-
ity. Basically, measures calculating similarity include
edge-based and node-based approaches (Pirr`o, 2009).
We adopt an edge-based measure since we have no
further topic information at hand but the topic re-
lations. The edge-based distance measure proposed
by (Sussna, 1993) supports our idea to integrate fur-
ther types of relations in future work and is designed
to work on hierarchies. This measure considers the
depth of a topic as well as the number of children
for similarity calculation. Equation 4 and 5 show the
weight calculation customized to our work.
ω
Sussna(p,c)
= 1 −
ω(p, c)
2· depth· distance
max
. (4)
given
ω(p, c) = 2−
1
|C
p
|
. (5)
The relation weight between to topics is divided
by the depth of the lower topic. This is called rela-
tive depth scaling. It is based on the assumption that
topics in lower levels are closer related than topics in
higher levels. Sussna calculates the distance between
topics. However, we want to model similarity, where
similarity = 1− distance. We need to normalize cal-
culated similarities to gain values between 0 and 1,
confer (Billig et al., 2010). To calculate similari-
ties, we first determine the distance values between all
topic pairs. We then divide distances by distance
max
calculated at the root level. Since the similarity at the
root level results in 0, we replace these weights by
1
|C
r
|
, where C
r
is the set of children of the root topic.
3.2.2 Normalize to Expert Standard
We define the expert standard by assuming that an on-
tology almost models the entire knowledge of a given
domain and that top experts in a topic have also top
expertise in its subtopics. When spreading a score to
the target topic we need to normalize the score against
the top expert level. We define the expert standard for
topic p as shown in Equation 6.
n
ExpertStandard
(p) =
∑
c∈C
p
100· ω
SussnaRoot
. (6)
where C
p
is the set of topic p’s children. Top expertise
is associated with scores of 100 points. In Equation
3, we normalize with n
ExpertStandard
. In case we cal-
culate n
ExpertStandard
based topic’s weight being pro-
cessed (say a topic at level 5), we drop relative depth
scaling and the weight in Equation 3 is reduced to
1
|C
p
|
. Instead, we use the weight at the root level. As
a consequence, for specific topics located on very low
levels, a learner does not have to show top expertise
in all of the subtopics to reach the maximum score. In
this case, it is probably sufficient to show nearly top
expertise in the sibling topics to reach 100 points in
the higher-level topic.
3.2.3 Coefficent α
The coefficient α alters a topic’s initial score as shown
in Equation 7.
α =
1
(1+ |C
active
|) · ω
p
· ω
f
. (7)
where C
active
is the set of active topics propagating
to topic p. ω
p
is the outgoing relation weight of p.
ω
f
is the outgoing relation weight of the farthest ac-
tive descendant in p’s subtree, where activation orig-
inally started. For instance in scenario 3, we calcu-
late α for the topic object-oriented with |C
active
| = 1,
ω
p
= 0.75 and ω
f
= 0.82. Coefficient α prevents in-
accuracies due to possibly coarse-grained source in-
formation in higher levels. We assume that exper-
tise scores of specific topics are more reliable than
that of general topics. For instance, a learner’s self-
assessment in a general topic is possibly more biased
than in a specific topic, which is usually easier to self-
assess. Therefore, the more information from specific
topics is available, the higher the loss of the general
topic. In addition, the higher the level of a topic be-
ing activated, the higher is the attenuation of its initial
score by means of ω
p
and ω
f
. The maximum score
a topic may receive is limited to the maximum score
of its children. For instance, three topics with scores
of 90, 80 and 70 points activate topic p. Then, the
maximum score of p is limited to 90 points.
4 EVALUATION
To measure the performance of the novel approach
against the baseline approach we set up various sce-
CSEDU2012-4thInternationalConferenceonComputerSupportedEducation
178
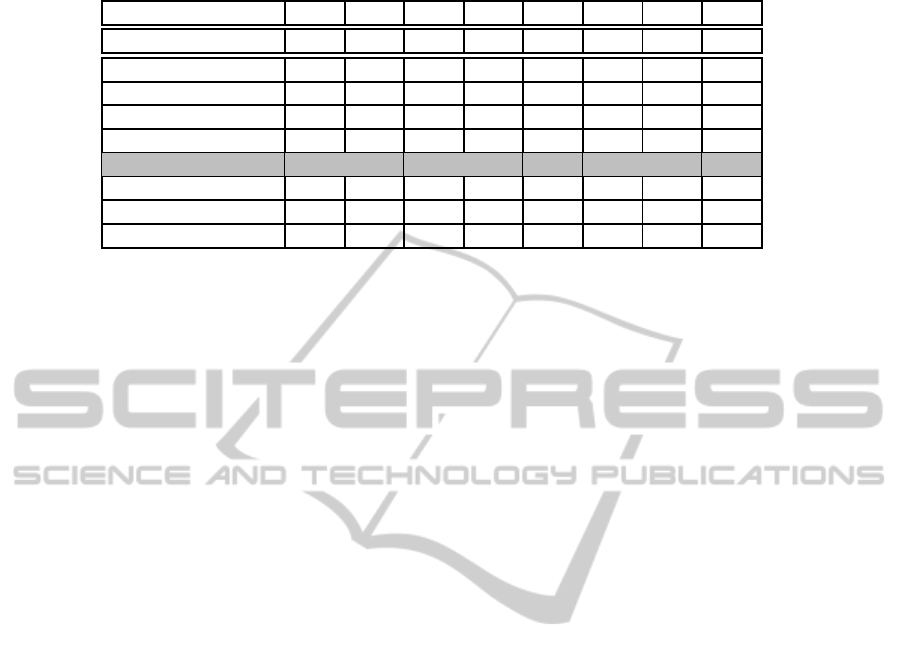
Table 2: Expertise scores calculated for the given scenarios.
Scenario 1 2 3 4 5 6 7 8
Baseline Approach 27.5 20.4 8.8 17.8 36.7 27.5 44.0 82.0
Novel Approach (γ)
(0.70) 25.3 9.0 5.0 11.3 45.2 33.9 39.3 56.5
(0.75) 29.1 11.1 6.0 12.9 48.5 39.2 41.0 58.9
(0.80) 33.1 13.5 7.0 14.7 51.7 45.1 42.8 61.4
(0.85) 37.3 16.3 8.2 16.6 54.9 50.9 44.5 63.8
(0.90) 41.9 19.4 9.6 18.6 58.1 57.1 46.3 66.3
(0.95) 46.6 22.9 11.1 20.7 61.4 63.6 48.1 68.7
(1.00) 51.7 26.8 12.7 23.0 64.6 70.5 49.8 71.2
narios serving as calculation tasks for both algo-
rithms. We then calculated expertise scores for each
scenario and asked experts to assess the scores by
means of an online survey. We had 29 participants
completing the survey, including professors, lecturers
and post-docs teaching programming courses at uni-
versity.
Test Scenarios. Table 1 shows the scenarios we
defined to test the algorithms in different hierarchy
levels and at different topic densities. Due to relative
depth scaling, we expect the novel algorithm to per-
form significantly better in scenarios with high den-
sity of topics located in lower levels (covered by sce-
narios 1, 5, 6). On the other side, we expect rather
similar behavior the more general and the more scat-
tered the topics are (Scenarios 2, 4). We also investi-
gate the propagation of scores on the same path test-
ing different path lengths (Scenarios 3, 7, 8).
Settings and Score Calculation. Before we started
calculation, we experimented with settings for the de-
cay factor γ. It seems reasonable to us that a one to
one relationship of two topics should nearly result in
equal scores for both topics. We performed propaga-
tion with varying decay factors and found that scores
of the topics Prolog and logic are nearly equal (Pro-
log: 50, logic: 52) at γ = 0.85. The baseline approach
works equally regarding a one to one relationship. Ta-
ble 2 shows the propagated scores given our scenar-
ios. As we expected, scenarios 2, 3, 4 and 7 show
almost identical results and scores are the closest at
γ = 0.85.
The difference in scores for scenarios 1, 5, 6 and 8
are worth to notice. We were interested, which scores
would be chosen by experts, if they had to vote for a
score showing the more accurate tendency.
Expert Survey. We set up an online survey and
asked for expert estimates. In particular, we wanted
to know how experts evaluate the scores in scenario
1, 5, 6 and 8 since these scenarios showed a clear
difference in score results. After a brief description
on how a beginner is distinguished from a top ex-
pert, we displayed for each scenario initial scores and
two calculated scores, one from the baseline the other
from the novel approach. Experts were asked: “Please
choose the score that in your opinion reflects the bet-
ter tendency for expertise ...”. Both the ontology
and the source of scores were hidden from the par-
ticipants. Since the scenarios’ initial scores are scaled
in ten steps, we carefully converted the result scores
to the same scale. We assume that this might facilitate
the decision-making of participants without causing a
bias. Scores were converted as follows: Scenario 1
with scores of 27.5/37.3 rounded to 30/40, scenario
5: 40/60, scenario 6: 30/50 and scenario 8: 60/80.
4.1 Results and Findings
Scenario 1 was intended to test the algorithms’ behav-
ior in lower levels with moderate topic density. 78%
of the domain experts perceived the scores coming
from the novel approach as more accurate. Scenario
5 aimed to test at lower levels with higher density of
topics. In this scenario 56% voted for novel approach.
In scenario 6 we observed the algorithms’ behavior
in lower levels propagating several levels towards the
top given a moderate topic density. Results show that
89% of the experts found the novel approach’s score
more accurate. Finally, scenario 8 was intended to
test the influence of coefficient α on a topic’s initial
score. The more specific information available, the
more initial score is attenuated. In contrast, the base-
line approach attenuates a propagated score more, the
higher the topic’s initial score is. 97% of the experts
favored the score calculated by the novel approach.
In summary, the novel approach outperforms the
baseline approach the lower the topics reside in the
hierarchy. Only the result of scenario 5 weakens this
claim. However, results of scenario 5 does not sig-
nificantly speak for the baseline either. Scenario 5 is
the one with the most given scores in the task descrip-
tion, which possibly makes expert assessments more
difficult and thus leads to a broader distribution of es-
SPREADINGEXPERTISESCORESINOVERLAYLEARNERMODELS
179

timates. The results also suggest that the coefficient
α is useful for altering initial scores. Despite of these
promising results, our study is not without shortcom-
ings, i.e., the small size of the ontology as well as the
small amount of scenarios tested so far. However, a
strong point is certainly the empirical assessment by
means of professors, lecturers and post-docs teaching
programming courses at university.
5 CONCLUSIONS
We proposed a novel algorithm to propagate expertise
scores in an ontology overlay model based on con-
strained spreading activation and relative depth scal-
ing. We compared the algorithm’s performance with
a baseline. 29 experts qualified calculated expertise
scores given various scenarios. Thereby, our algo-
rithm outperforms the baseline approach in half of
the test scenarios. For the remaining scenarios both
algorithms propagate almost equally. These results
suggests that the calculation of a learner’s expertise
utilizing constrained spreading activation and relative
depth scaling can lead to more accurate learner mod-
els. Future work may consider multi-inheritance of
topics as well as the integration of additional relation
types like the part-of relationship.
REFERENCES
Anderson, J. (1983). A spreading activation theory of mem-
ory. Journal of verbal learning and verbal behavior,
22(3):261–295.
Billig, A., Blomqvist, E., and Lin, F. (2010). Semantic
matching based on enterprise ontologies. On the Move
to Meaningful Internet Systems 2007: CoopIS, DOA,
ODBASE, GADA, and IS, pages 1161–1168.
Brusilovsky, P. and Mill´an, E. (2007). User models for
adaptive hypermedia and adaptive educational sys-
tems. The adaptive web, pages 3–53.
Bull, S. and Kay, J. (2010). Open learner models. Advances
in Intelligent Tutoring Systems, pages 301–322.
Cantador, I., Szomszor, M., Alani, H., Fern´andez, M., and
Castells, P. (2008). Enriching ontological user profiles
with tagging history for multi-domain recommenda-
tions. In 1st Int. Workshop on Collective Intelligence
and the Semantic Web (CISWeb 2008).
Carr, B. and Goldstein, I. (1977). Overlays: A theory
of modelling for computer aided instruction. Artifi-
cial Intelligence Memo 406, Massachusetts Institute
of Technology, Cambridge, Massachusetts.
Cohen, P. and Kjeldsen, R. (1987). Information re-
trieval by constrained spreading activation in seman-
tic networks. Information processing & management,
23(4):255–268.
Crestani, F. (1997). Application of spreading activation
techniques in information retrieval. Artificial Intelli-
gence Review, 11(6):453–482.
Kay, J. and Lum, A. (2005a). Exploiting readily available
web data for scrutable student models. In Proceedings
of the 2005 conference on Artificial Intelligence in Ed-
ucation: Supporting Learning through Intelligent and
Socially Informed Technology, pages 338–345. IOS
Press.
Kay, J. and Lum, A. (2005b). Ontology-based user mod-
elling for the semantic web. In Proceedings of the
Workshop on Personalisation on the Semantic Web:
Per-SWeb05, pages 15–23.
Liu, H. and Maes, P. (2005). Interestmap: Harvesting social
network profiles for recommendations. In Beyond Per-
sonalization - IUI 2005, San Diego, California, USA.
Liu, W., Weichselbraun, A., Scharl, A., and Chang, E.
(2005). Semi-automatic ontology extension using
spreading activation. Journal of Universal Knowledge
Management, 1:50–58.
Manouselis, N., Drachsler, H., Vuorikari, R., Hummel, H.,
and Koper, R. (2011). Recommender systems in tech-
nology enhanced learning. Recommender Systems
Handbook, pages 387–415.
Pirr`o, G. (2009). A semantic similarity metric combin-
ing features and intrinsic information content. Data
Knowl. Eng., 68(11):1289–1308.
Schickel-Zuber, V. and Faltings, B. (2007). Oss: a semantic
similarity function based on hierarchical ontologies.
In Proceedings of the 20th international joint confer-
ence on Artifical intelligence, pages 551–556.
Sieg, A., Mobasher, B., and Burke, R. (2007). Web search
personalization with ontological user profiles. In Pro-
ceedings of the sixteenth ACM conference on Con-
ference on information and knowledge management,
pages 525–534. ACM.
Sussna, M. (1993). Word sense disambiguation for free-
text indexing using a massive semantic network. In
Proceedings of the second international conference on
Information and knowledge management, pages 67–
74. ACM.
CSEDU2012-4thInternationalConferenceonComputerSupportedEducation
180
