
MINING ON THE CLOUD
K-means with MapReduce
Ilias K. Savvas
1
and M-Tahar Kechadi
2
1
Dept. of Computer Science and Telecommunications, T.E.I. of Larissa, Larissa, Greece
2
School of Informatics and Computer Science, UCD, Dublin, Ireland
Keywords:
MapReduce, HDFS, Hadoop, Clustering, K-means Algorithm.
Abstract:
The Apache Hadoop software library is a framework for distributed processing of large data sets, while HDFS
is a distributed file system that provides high-throughput access to data-driven applications, and MapReduce
is software framework for distributed computing of large data sets. The huge collections of raw data require
fast and accurate mining process in order to extract useful knowledge. One of the most popular techniques
of data mining is the K-means clustering algorithm. In this paper, we developed a distributed version of the
K-means algorithm using the MapReduce framework on the Hadoop Distributed File System. The theoretical
and experimental results of the technique proved its efficiency.
1 INTRODUCTION
Nowadays, computational systems and science instru-
ments generate petascale data stores. For example,
the Large Synoptic Survey Telescope (LSST, 2011)
generates several petabytes of data each year, while
the Square Kilometer Array generates 200 Gbytes or
raw data per second (SKA, 2011). Cyber security has
to handle huge raw datasets and should provide ac-
tionable results in seconds to minutes while social
computing stores vast amount of content that must
managed, searched, and delivered to users over the
Internet. Thus, the computational applications are be-
coming data-centric (Gorton et al., 2008). With Data
Intensive Computing, organizationscan progressively
filter, transform and process massive data volumes
into information that helps the users make better de-
cisions sooner.
Data Mining is the process for extracting useful
information from large data-sets. One of the most
important techniques of data mining clustering is the
k-means algorithm (LLoyd, 1982). K-means takes
as inputs the desired number of clusters k, and a
dataset. It assigns data objects to the clusters accord-
ing to a certain similarity measure. As the datasets
are very large, the operation of assigning and/or re-
assigning data objects to their nearest centroids is
very time consuming. One method is to distribute the
dataset among a set of processing nodes and perform
the calculation of centroids in parallel. This method
follows the Single Program Multiple Data (SPMD)
paradigm. It can be implemented by using threads,
MPI or MapReduce (HMR, 2011).
The purpose of this study is to explore the pos-
sibility of using Hadoop’s MapReduce framework
(AH, 2011) and the Hadoop Distributed File System
-HDFS- (Dean and Ghemawat, 2008) to implement
a popular clustering technique in a distributed fash-
ion. The experimental results obtained so far are very
promising and showed good performance of the pro-
posed technique. In addition, the theoretical analysis
of the complexity of the algorithm is inline with the
experimental results, the approach scales very well
and outperforms the sequential original version.
The rest of the paper is organised as follows. The
related work is presented in Section 2. In Section 3
the proposed algorithms are presented. Section 4
presents the experimental results and in Section 5 we
discuss the complexity issues of the techniques. Fi-
nally, Section 6 concludes the paper and highlights
some future research directions.
2 RELATED WORK
There have been extensive studies on various clus-
tering methods; and especially the k-means clus-
tering has been given a great attention. However,
there is very little on the application of k-means to
413
K. Savvas I. and Kechadi M..
MINING ON THE CLOUD - K-means with MapReduce.
DOI: 10.5220/0003927204130418
In Proceedings of the 2nd International Conference on Cloud Computing and Services Science (CLOSER-2012), pages 413-418
ISBN: 978-989-8565-05-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

the MapReduce. Since its early development, the
k-means clustering (LLoyd, 1982) has been identi-
fied to have a very high complexity and significant
effort has been spent to tune the algorithm and im-
prove its performance. While k-means is very simple
and straightforward algorithm, it has two main issues:
1) the choice of the number of clusters and of the ini-
tial centroids. 2) the iterative nature of the algorithm
which impacts heavily on its scalability as the size of
the dataset increases. The right set of initial centroids
will lead to compact and well formed clusters (Jin
et al., 2006). On the other hand, in (McCallum et al.,
2000) and (Guha et al., 1998), the authors explained
how the number of iterations can be reduced by parti-
tioning the dataset into overlapping subsets and iterat-
ing only over the data objects within the overlapping
areas. This technique is called Canopy Clustering.
While the above studies largely concentrated on
improving the k-means algorithm and reducing the
number of iterations, there have been many other
studies about its scalability. Recently, more research
has been done on MapReduce framework. The paper
(Zhao et al., 2009) presented Parallel k-means cluster-
ing based on MapReduce. It has been shown that the
k-means clustering algorithms can scale well and can
be parallelized. The authors concluded that MapRe-
duce can efficiently process large datasets.
Some researches have conducted comparative
studies of various MapReduce frameworks available
in the market and studied their effectiveness in the
area of clustering large datasets. In (S.Ibrahim et al.,
2009), the authors have analysed the performance
benefits of Hadoop on virtual machines, and it was
shown that MapReduce is a good tool for cloud
based data analysis. There have been also devel-
opments with Microsoft product DryadLINQ to per-
form data intensive analysis and compared the per-
formance of DryadLINQ with Hadoop implementa-
tions (Ekanayake et al., 2009). In another study, the
authors have implemented a slightly enhanced model
and architecture of MapReduce called the
Twister
(Ekanayake et al., 2010). They have compared the
performance of Twister with Hadoop and DryadLINQ
with the aim of expanding the applicability of MapRe-
duce for data-intensive scientific applications. Two
important observations can be made from this study.
First, for computationintensiveworkload, threads and
processes did not show any significant difference in
performance. Second, for memory intensive work-
load, processes are 20 times faster than threads. In
(Jiang et al., 2009) a comparative study of Hadoop
MapReduce and Framework for Rapid Implemen-
tation of data mining Engines has been performed.
According to this study, they have concluded that
Hadoop is not well suited for modest-sized databases.
However, when the datasets are large, there is a good
performance benefit in using Hadoop.
3 MAPREDUCE K-MEANS
TECHNIQUE
The sequential k-means algorithm starts by choosing
k initial centroids, one for each cluster and assigns
each object of the dataset to the nearest centroid. Then
it recalculates the centroid of each cluster based on
its member objects and goes through again each data
object and assigns it to its closest centroid. This step
is repeated until there is no change in the centroids.
In this work we transformed the original k-means
algorithm to meet the MapReduce requirements. The
new k-means technique consists of four parts: a map-
per, a reducer, a mapper with a combiner, and a re-
ducer with a combiner.
3.1 Mapper and Reducer (MR)
The input dataset is distributed across the mappers.
The initial set of centroids is either placed in a com-
mon location and accessed by all the mappers or dis-
tributed on each mapper. The centroid list has an
identification for each centroid as a key and the cen-
troid itself as the value. Each data object in the sub-
set (x
1
,x
2
,...,x
m
) is assigned to its closest centroid by
the mapper. We use the Euclidean distance to mea-
sure proximity of data objects; the distances between
a data object and the centroids. The data object is as-
signed to the closest centroid. When all the objects
are assigned to the centroids, the mapper sends all the
data objects and the centroids they are assigned to, to
the reducer (Algorithm 1).
After the execution of the mapper, the reducer
takes as input the mapper outputs,
(key, value)
pairs,
and loops through them to calculate the new centroid
values. For each centroid, the reducer calculates a
new value based on the objects assigned to it in that
iteration. This new centroid list is sent back to the
start-up program (Algorithm 2).
3.2 Mapper and Reducer with
Combiner (MRC)
In the MapReduce model, the output of the map func-
tion is written to the disk and the reduce function
reads it. In the mean time, the output is sorted and
shuffled. In order to reduce the time overhead be-
tween the mappers and the reducer, Algorithm 1 was
modified to combine the map outputs in order to re-
CLOSER2012-2ndInternationalConferenceonCloudComputingandServicesScience
414

Algorithm 1: Algorithm for Mapper.
Require:
• Subset of m-Dim objects {x
1
,x
2
,..., x
n
} in each map-
per
• Initial set of centroids C = {c
1
,c
2
,...,c
k
}
1: M ← {x
1
,x
2
,..., x
n
}
2: current centroids ← C
3: out putlist ← ∅
4: for all x
i
∈ M do
5: bestCentroid ← ∅
6: minDist ← ∞
7: for all c ∈ current centroids do
8: dist ← kx
i
,ck
9: if bestCentroid = ∅ or dist < minDist then
10: minDist ← dist
11: bestCentroid ← c
12: end if
13: end for
14: outputlist ← outputlist ∪ (bestCentroid, x
i
)
15: end for
16: return outputlist
Algorithm 2: Algorithm for Reducer.
Require: Input (key, value) where key = bestCentroid, and
value = objects assigned to the centroids by the mapper.
1: out putlist ← outputlists from mappers
2: v ← ∅
3: newCentroidList ← ∅
4: for all y ∈ outputlist do
5: centroid ← y.key
6: object ← y.value
7: v
centroid
← ob ject
8: end for
9: for all centroid ∈ v do
10: newCentroid, sumofObjects,numof Ob jects ← ∅
11: for all object ∈ v do
12: sumof Ob jects ← sumof Objects+ object
13: numof Ob jects ← numof Ob jects+ 1
14: end for
15: newCentroid ← (sumof Ob jects÷ numofOb jects)
16: newCentroidList ← newCentroidList ∪ newCentroid
17: end for
18: return newCentroidList
duce the amount of data that the mappers have to write
locally and the reducer to read it. The proposed com-
biner reads the mapper outputs locally, and calculates
the local centroids. After that, the reducer reads the
output produced by the mappers (which is only the
local centroids instead of the entire dataset) and cal-
culates the global centroids. This method reduces dra-
matically the read/write operations. The mappers and
reducer now are using the combiner, which are de-
scribed in Algorithms 3, and 4 respectively.
Algorithm 3: Algorithm for Mapper with Combiner.
Require:
• A subset of d-dimensional objects of {x
1
,x
2
,.. ., x
n
} in
each mapper
• Initial set of centroids C = {c
1
,c
2
,.. . , c
k
}
1: M ← {x
1
,x
2
,.. ., x
n
}
2: current centroids ← C
3: outputlist ← ∅
4: v ← ∅
5: for all x
i
∈ M do
6: bestCentroid ← ∅
7: minDist ← ∞
8: for all c ∈ current centroids do
9: dist ← kx
i
,ck
10: if bestCentroid = ∅ or dist < minDist then
11: minDist ← dist
12: minDist ← dist
13: end if
14: end for
15: v
bestCentroid
← x
i
16: end for
17: for all centroid ∈ v do
18: localCentroid ← ∅
19: sumofLocalobjects ← ∅
20: numofLocalObjects ← ∅
21: for all ob ject ∈ v do
22: sumofLocalObjects ← sumofLocalObjects +
object
23: numofLocalObjects ← numofLocalObjects + 1
24: end for
25: localCentroid ← (sumofLocalObjects ÷
numofLocalObjects)
26: outputlist ← (centroid, localCentroid)
27: end for
28: return outputlist
Algorithm 4: Algorithm for Reducer with Combiner.
Require: Input (key, value) where key = oldCentroid and value
= newLocalCentroid assigned to the centroid by the mapper.
1: outputlist ← outputlists from mappers
2: v ← ∅
3: newCentroidList ← ∅
4: for all y ∈ outputlist do
5: centroid ← y.key
6: localCentroid ← y.value
7: v
centroid
← localCentroid
8: end for
9: for all centroid ∈ v do
10: newCentroid ← (sumofLocalCentroids ÷
numofLocalCentroids)
11: newCentroidList ← newCentroidList ∪ newCentroid
12: end for
13: return newCentroidList
MININGONTHECLOUD-K-meanswithMapReduce
415

4 EXPERIMENTAL RESULTS
To evaluate the proposed MapReduce K-means tech-
nique, we use a cluster of 21 nodes. One of the nodes
is defined as Namenode and Job Tracker and has an
Intel Pentium IV cpu of 3.4GHz and 2GB of main
memory. The remaining nodes are defined as Datan-
odes and Task Trackers; each of them has an Intel dual
Core cpu of 2.33GHz and 2GB of main memory. The
network has a bandwidthof 1Gbps. All nodes run Red
Hat version 4.1.2−48 and 32bit operating system 5.5.
We used Java Runtime version 1.6.0 16, Python 2.4.3
and Hadoop 0.21.0.
4.1 Input Datasets
We use spatial data for testing for many reasons. The
distance measure, Euclidian distance, is well suited
for such data, the spatial dimensions are very com-
plex, as their combination with the Euclidian distance,
define spherical shapes, which are not always desir-
able. We generated datasets containing clusters of
different shapes, densities and noise. So, the primary
dimensions are the spacial dimensions, we generated
about 2G data objects of 2D and 3D. The 3d dataset
before clustering is shown in Figure 1.
Figure 1: 3d-Dataset.
4.2 Results' Analysis
As a first step of the k-means algorithm we have con-
sidered various methods, from random choice of cen-
troids to canopy clustering, to generate initial cen-
troids. Because the quality of the final clusters in k-
means depends highly on the first step (initial genera-
tion of centroids), we decided against random choice.
Instead, we chose a more dependable approach of the
density distribution of the data objects. This worked
well for our study as our aim was not to optimise the
choice of initial set of centroids but to analyse the ef-
fectiveness of MapReduce to cluster. The final clus-
tered 3d data points are shown in Figure 2.
Figure 2: Final clusters of 3d data.
With the Hadoop characteristics in mind, we have
improved the clustering response time. We also stud-
ied the effect of the number of nodes on the speed of
convergence of the clustering technique. So we used
the same set of data objects and perform the MapRe-
duce with just one node and gradually, we increased
the number of nodes up to 21. As the number of nodes
increases, the MapReduce k-means algorithm conver-
gences faster. For example, a dataset of 100K data
objects, it takes about 110 seconds with one node to
converge and 71 seconds with 4 nodes. It is far from
an ideal speedup but it is an improvement of 35%.
Another very interesting point is the behaviour of
the technique when the number of clusters, k, varies.
As we can see in Table 1 increasing the number of
clusters, the performance of the proposed technique
is also increasing. For example, for k = 2, the simple
MapReduce algorithm needs at least 8 participating
nodes in order to outperform the sequential algorithm
when the number of data objects is about N = 10 mil-
lions, and only 2 nodes when k = 10. Basically, more
k is bigger more the technique needs to be distributed,
because more computations are required to assign the
objects to their corresponding clusters, and therefore,
the overhead of the MapReduce procedure becomes
less important.
Table 1: Number of nodes needed to outperform the sequen-
tial technique.
N k=2 k=4 k=10
MR MRC MR MRC MR MRC
10 >20 6 7 2 2 2
100 11 2 10 2 2 2
500 16 2 16 2 2 2
1000 >20 2 20 3 2 2
More precisely, in Figures 3, and 4 we can see
the behaviour of the proposed technique with 3 dif-
ferent numbers of clusters. The number of participat-
ing nodes varied from 1 to 21 (x-axis), while keep-
ing constant the number of data objects to 1 billion.
CLOSER2012-2ndInternationalConferenceonCloudComputingandServicesScience
416
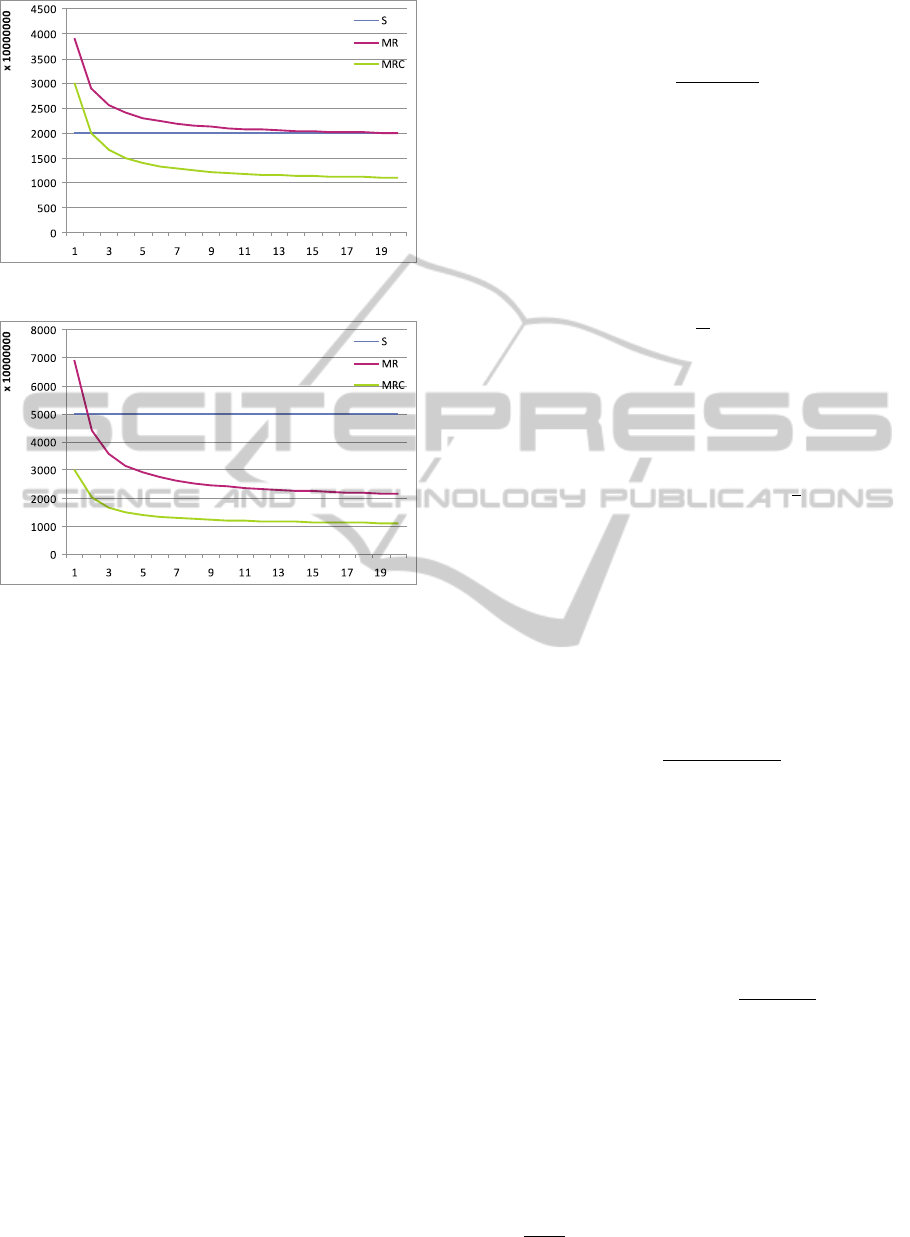
Figure 3: Time to cluster 1 billion 3d points (k=4).
Figure 4: Time to cluster 1 billion 3d points (k=10).
As the number of the clusters k and the number of
nodes increase, the efficiency of MapReduce k-means
increases.
5 MAPREDUCE K-MEANS
COMPLEXITY
In this section we validate theoretically the experi-
mental results obtained in the previous section.
Complexity of the Sequential Algorithm. In the
sequential k-means clustering the time coplexity is
given by the equation 1 (LLoyd, 1982).
T
S
(N) = M × k × N (1)
where k is the number of clusters, N is the number
of data objects, and M is the number of iterations.
Complexity of the MapReduce Algorithm. Mapper:
Before using MapReduce for clustering, we need to
partition the input data objects into x subsets, where
x is the number of available mappers. In each map-
per, we iterate through N/x data objects and for each
centroid in the k clusters, for calculating the distance
between them and assign for each objects its corre-
sponding centroid. So, the complexity of the mapper
is expressed by the following equation 2.
T
M
(N) =
M × k × N
x
(2)
Reducer: In the reducer, we iterate through the output
from x mappers for assigning each object and its cor-
responding centroid into a dictionary type variable for
further processing. We then iterate through each cen-
troid k, by cumulating and counting the data objects in
that cluster and calculate a new centroid. Therefore,
the complexity of this operation is given by equation
3.
T
R
(N) = M(N + k
N
k
) = 2M × N (3)
We repeat the MapReduce process M times until
convergence. So, according to the equations 2 and 3
the total complexity for the MapReduce algorithm is
as follows:
T
MR
(N) = T
M
(N) + T
R
(N) = M × N
k
x
+ 2
(4)
Where x is the number of nodes assigned for the
MapReduce K-means process.
Complexity of MapReduce with Combiner. Mapper
with Combiner: In the mapper, we iterate through all
the N/x data objects for each centroid to calculate the
distances between them while the combiner calculates
the k centroids each time the mappers terminate their
process. Therefore, the complexity now is as follows:
T
MC
(N) =
M × k × N + N
x
(5)
Reducer: In the reducer, we iterate through k outputs
from x mappers to calculate the global centroids.
T
RC
(N) = N + k (6)
We repeat the entire process for M iterations un-
til convergence. Thus, the total complexity of the
MapReduce with Combiner algorithm is as follows:
T
MRC
(N) = T
MC
(N) + T
RC
(N) =
MkN + N
x
+ N + k
(7)
where x is the number of nodes assigned for the
MapReduce K-means process.
Comparing the above mentioned complexities we
can see the following:
Sequential vs. MapReduce. From equations 1, and 4
we can easily see that
MkN
x
+ 2MN ≤ MkN, ∀(k > 2∧ x > 3) (8)
MININGONTHECLOUD-K-meanswithMapReduce
417

Thus, for any k > 2 and the number of the partic-
ipating nodes is greater than 3 then the MapReduce
k-means version outperforms the sequential one.
MapReduce vs. MapReduce with Combiner. From
equations 4, and 7 we can derive the following:
N
x
+ N + k ≤ 2MN, ∀(x ≥ 1∧ M > 1)
Therefore, the MapReduce with Combiner tech-
nique outperforms the simple MapReduce technique
even with one processing node and the number of iter-
ations is more than 2 and in addition, the experimental
results are inline with the theoretical analysis.
6 CONCLUSIONS
In this study, we have adapted the MapReduce tech-
nique to the k-means clustering algorithm. We de-
scribe the new technique and discuss its theoretical
complexity. We validated our implementation by ex-
periments on a cluster of workstations. The results
show that the clusters formed using MapReduce are
identical to the clusters formed using the sequential
(original) algorithm. We also showed that by adding
a combiner between Map and Reduce jobs improves
the performanceby decreasing the amount of interme-
diate read/write operations. In addition, the number
of available nodes for the map tasks increases signifi-
cantly the performance of the system.
As near future work we would like to; 1) Evaluate
the performance of the proposed techniques on a very
large number of heterogeneous computing resources
(nodes) since one of the main problemsof the MapRe-
duce is that all the mappers have to finish their jobs
before starting the reduce phase. 2) Express explic-
itly the overhead produced from both the MapReduce
technique and the read/write operations as a function
of the size of the input dataset and the number of the
nodes (T
o
= f(N,x)).
REFERENCES
AH (2011). Apache Hadoop. http://hadoop.apache.org.
Dean, J. and Ghemawat, S. (2008). Mapreduce: Simplified
data processing on large clusters. Communications of
the ACM, 51(1):107–113.
Ekanayake, J., Gunarathne, T., Fox, G., Balkir, A. S.,
Poulain, C., Araujo, N., and Barga, R. (2009).
Dryadlinq for scientific analyses. Fifth IEEE Inter-
national Conference on e-Science (E-SCIENCE '09),
pages 329–336.
Ekanayake, J., Li, H., Zhang, B., Gunarathne, T., Bae, S.,
Qiu, J., and Fox, G. (2010). Twister: a runtime for iter-
ative mapreduce. 19th ACM International Symposium
on High Performance Distributed Computing, pages
810–818.
Gorton, I., Greenfield, P., Szalay, A., and Williams, R.
(2008). Data-intensive computing in the 21st century.
IEEE Computer, pages 78–80.
Guha, S., Rastogi, R., and Shim, K. (1998). Cure: an effi-
cient clustering algorithm for large databases. ACM
SIGMOD International Conference on Management
of Data, pages 73–84.
HMR (2011). Hadoop MapReduce. http://
hadoop.apache.org/mapreduce/.
Jiang, W., Ravi, V., and Agrawal, G. (2009). Compar-
ing map-reduce and freeride for data-intensive appli-
cations. IEEE International Conference on Cluster
Computing and Workshops, pages 1–10.
Jin, R., Goswami, A., and Agrawal, G. (2006). Fast and
exact out-of-core and distributed k-means clustering.
Knowledge and Information Systems, 10(1):17–40.
LLoyd, S. P. (1982). Least squares quantization in pcm.
IEEE Transactions on Information Theory, 28:129–
137.
LSST (2011). Large Synoptic Survey Telescope. http://
www.lsst.org/lsst.
McCallum, A., k. Nigam, and Ungar, L. H. (2000). Ef-
ficient clustering of high-dimensional data sets with
application to reference matching. ACM SIGKDD In-
ternational Conference on Knowledge Discovery and
Data Mining, pages 169–178.
S.Ibrahim, Jin, H., Lu, L., Qi, L., Wu, S., and Shi,
X. (2009). Evaluating mapreduce on virtual ma-
chines: The hadoop case. 1st International Confer-
ence on Cloud Computing, Springer: Cloud Comput-
ing 5931:519–528.
SKA (2011). Square Kilometer Array. http://
www.skatelescope.org/.
Zhao, W., Ma, H., and He, Q. (2009). Parallel k-means clus-
tering based on mapreduce. 1st International Confer-
ence on Cloud Computing, Springer: Cloud Comput-
ing 5931:674–679.
CLOSER2012-2ndInternationalConferenceonCloudComputingandServicesScience
418
