
A COMPARATIVE STUDY OF IMPLEMENTED COLLISION
DETECTION STRATEGIES
F´elix Paulano, Juan J. Jim´enez, Rub´en Pulido and Carlos J. Ogayar
Departamento de Inform´atica, University of Ja´en, Ja´en, Spain
Keywords:
Collision Detection, Spatial Decomposition, Bounding Hierarchy, Strategies Comparative.
Abstract:
Many computer interactive environments require to calculate collision detections between geometrical models,
usually triangle meshes. In this paper, a comparative study of some collision detection strategies is realized.
For this purpose, the compared algorithms have been implemented. Some of these algorithms also allow
realizing other procedures, such as calculating distances or overlapping triangles. Hence, the main features
of each algorithm have been explained. The compared strategies have been tested considering, in addition
to the runtime, the pre-processing time and the memory usage. Finally, the results have been compared in
order to extract the benefits and constraints of each strategy, and proposing some possible applications for
each strategy.
1 INTRODUCTION
Interactive environments require methods that allow
performing collision detection tests between geo-
metrical models, usually triangle meshes (Lin and
Gottschalk, 1998; Bergen, 2003). Since interaction
must be in real time, it is necessary to utilize methods
that resolve the collision detection quickly. In addi-
tion, the methods must be robustso that the interactive
environment remains consistent.
Once the collision is detected, the interactive en-
vironment must give a response (Geiger, 2000). For
that, it is important not only to detect the collision, but
also to calculate a detailed collision. This involves
calculating some collision parameters, such us over-
lapping triangles, distances, and nearest points. These
calculations must be also calculated quickly in order
to keep a real time interaction.
In the literature, there are several approaches that
allow performing some of that calculations. Each ap-
proach has their advantages and disadvantages, hence
the use of one method depends on each situation. In
the present paper, we describe strategies to calculate a
detailed collision between two triangle meshes. These
strategies are implemented in order to test and com-
pare them. These tests allow extracting the main ben-
efits and constraints of each strategy.
The following section deals with the proposed
strategies. Then, we will explain the implementations
and makea comparison between the differentstrategi-
es. Later, a possible GPU implementation of the pro-
posed strategies is studied. Finally, the benefits and
constraints of each strategy are shown and some ap-
plications or each approach are suggested.
2 PROPOSED STRATEGIES
In order to perform a collision detection, we have
proved different strategies and determined their posi-
tive and negative points. On the one hand, we pretend
to calculate the collision detection. On the other hand,
we want to identify other features that allow us to im-
plement a correct response to a collision.
2.1 Spatial Decompositions
Hierarchical space decompositions allow increasing
the efficiency of the collision detection. This is be-
cause spatial decompositions permit to reduce the
space where the collision detection is performed. In
order to check a collision, the two spatial decompo-
sitions are compared recursively. Each recursive step
tests whether two nodes A and B, one from each hier-
archy, collide. If A and B do not collide, the collision
test ends. Otherwise, the collision test is performed
recursively to their children. If A or B are both leaf
nodes, the collision detection test is performed to the
triangles that are inside the leaf nodes. When down
485
Paulano F., J. Jiménez J., Pulido R. and J. Ogayar C..
A COMPARATIVE STUDY OF IMPLEMENTED COLLISION DETECTION STRATEGIES.
DOI: 10.5220/0003930604850490
In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 485-490
ISBN: 978-989-8565-02-0
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

the hierarchy, some different strategies can be chosen.
For example, if A and B do not collide, we can test A
with each of the children of B, B with each of the chil-
dren of A, or each of the children of A with each of
the children of B. This choice modifies the efficiency
of the method and depends on each case.
In order to perform the triangle-triangle collision
test, we have used the point in solid algorithm by
Feito (Feito and Torres, 1997). This method allows
performing a point in solid test without any complex
calculation, such as solving a system of equations. In
addition, this method is robust because it can work
with non-manifold polyhedra.
The octree (Chen and Huang, 1988) is one of the
most used hierarchical data structures. This structure
starts from a cuboid that contains all the triangles,
usually a bounding box. In general, the root box is
homogeneously divided into eight new boxes. The
subdivision stops when a prefixed level is reached or
a box contains less triangles than a threshold. There
are variations in the octree that can improve its per-
formance. One of the most used proposes a change
in the subdivision method of the boxes. Instead of di-
viding homogeneously each box, the dividing point is
selected so that it increases the efficiency.
The tetra-tree (Jim´enez et al., 2006) is a hierar-
chical data structure that divides the entire space into
eight equal parts named tetra-cones. In the follow-
ing levels of the hierarchy, each tetra-cone is homo-
geneously divided into four new tetra-cones. Due to
the adjustment obtained by bounding tetrahedra as-
sociated with each tetra-cone (Jim´enez and Segura,
2008), the tetra-tree fits the mesh better that other ap-
proaches, such as the octree. In addition, the tetra-
tree allows classifying triangles quickly and robustly
because it is based on barycentric coordinates. In the
same way as the octree, the subdivision stops when a
prefixed level is reached or a tetra-cone contains less
triangles than a threshold.
2.2 Convex Hull
Convex objects enable the application of specific al-
gorithms in order to detect a collision. In general,
these algorithms are more efficient because they take
advantage of the convex object features. We consid-
ered to build the convex hull of the objects in order to
apply specific algorithms, such us the GJK algorithm
(Gilbert et al., 1987) or some of its variants (Cameron,
1997). The quick hull method was chosen to build the
convex hull. Nevertheless, the main disadvantage is
that the convex hulls do not fit the mesh properly in
most cases, hence the obtained results are not exact.
2.3 Bounding Volume Hierarchies
As an alternative to spatial decompositions and con-
vex hulls, we propose to use bounding volume hierar-
chies (Gottschalk et al., 1996; Klosowski et al., 1998).
Unlike the spatial decompositions, bounding volumes
do not fill all the space and their nodes can overlap
between them.
In (Larsen et al., 1999), swept sphere hierarchies are
used to perform collision detections, identify over-
lapping triangles, determine nearest points, and cal-
culate distances. They used three different types of
swept volumes: a sphere, a cylinder with hemispher-
ical caps, and a rounded box. These volumes depend
on the swept primitive used: a point, a segment, and a
rectangle. The algorithm efficiency depends on the
volume used. The sphere allows building the data
structure quickly, but the rounded box fits the mesh
better.
This algorithm utilizes a bounding volume traver-
sal tree (BVTT) in order to perform a query. Each
node of the BVTT represents a single collision test
between two bounding volumes. Hence, the BVTT
is traversed to perform a collision detection. In or-
der to improve query performance, this method uses a
priority directed search when the BVTT is being tra-
versed. Moreover, temporal coherence is also taken
into account. This method is implemented in the PQP
library.
In (Ehmann and Lin, 2001), they present an ap-
proach to detect collisions and calculate distances
based on convex surface decomposition. Moreover,
This method has three main steps. First, the model
is decomposed into convex parts. In order to achieve
that, a method based on graph search is used. Second,
a bounding volume hierarchy is constructed based on
the previous decomposition. They proposed a top-
down approach in which each node of the hierarchy
bounds all the geometry in its child nodes. For that
reason, the primitives are divided recursively in order
to obtain new convex patches.
Once the hierarchy is constructed, queries can
be executed. In order to perform queries between
pairs of convex polyhedra, the method uses a distance
minimization algorithm based on Voronoi marching
(Ehmann and Lin, 2000). Queries are accelerated us-
ing spatial and temporal coherence. This method re-
quires 2-manifold meshes and their triangles must be
sorted counter-clockwise. This algorithm is imple-
mented in the SWIFT++ library.
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
486
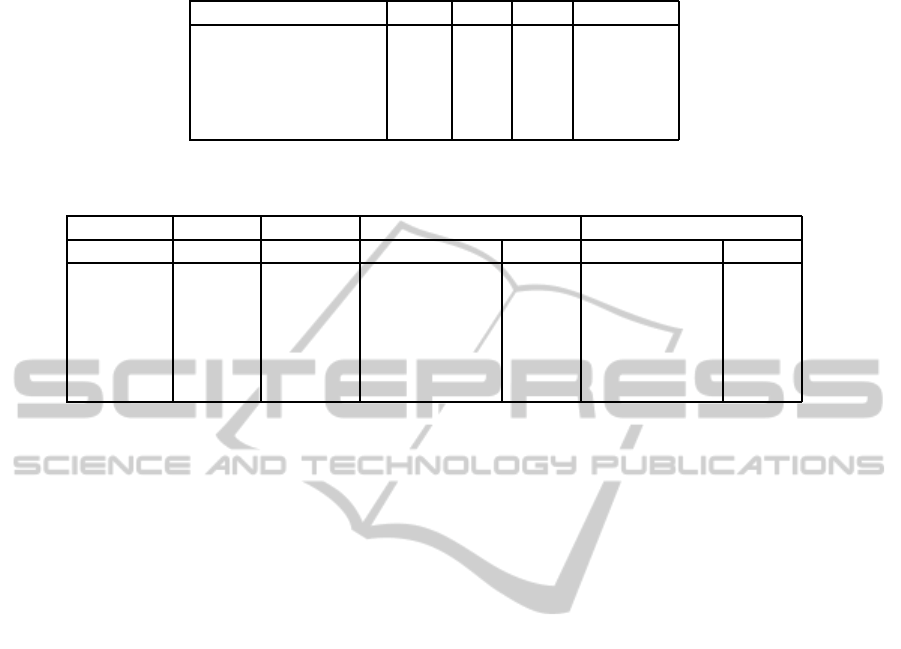
Table 1: Features implemented by each method. Tetra-tree and Octree utilize the Feito- Torres algorithm.
Feito GJK PQP SWIFT++
Collision X X X X
Overlapping triangles X X
Distance X X X
Tolerance X X
Contact features X
Table 2: Pre-processing time (s) and size (MB) of the spatial decompositions.
Tetra-tree Octree
Vertices Triangles Pre-processing Size Pre-processing Size
Horse 3582 7172 0,427 0,0351 0,496 0,0399
Skull 20002 40000 2,49 0,2608 4,329 0,261
Bunny 35947 69451 4,544 0,4211 8,744 0,3254
Armadillo 172974 345944 28,184 2,0322 44,579 1,6549
Dragon 437645 869928 70,25 4,8031 104,68 2,1975
Buddha 543652 1085634 84,704 5,5607 138,542 4,8717
3 IMPLEMENTATION AND
RESULTS
In order to check their performance, the described
strategies have been implemented under the same
conditions. In order to developed this, we have used
the same programming language (C++) and the same
compiler (gcc). The implemented data structures are
the octree and the tetra-tree. The Feito’s algorithm has
been used to check the intersection between triangles.
In addition, qhull, PQP, and SWIFT++ libraries have
been used.
Spatial decompositions, as well as the Feito and
Torres algorithm have been implemented without the
use of any library. Moreover, we have not used any
optimization, nor have considered spatial or tempo-
ral coherence. That means that the implementation is
less optimized than other approaches which are based
on a library. Hence, the obtained results should not
be as good as the implemented libraries. In order
to implement the convex hull, the qhull library has
been utilized. This library implements the quickhull
algorithm and is one of the most used libraries. Nev-
ertheless, the collision detection based on the qhull
implementation has not been tested because the re-
sults obtained are not as accurate as the rest of ap-
proaches, hence the obtained results should not be
compared with them. The PQP library, that is writ-
ten in C++, can work with any model composed of
triangles. Hence, it is not necessary that the mesh is
closed or 2-manifold. This library allows detecting
collisions and overlapping triangles, calculating dis-
tances and nearest points, and determining if two
models are closer than a given threshold. The
SWIFT++ library is implemented in C++ and is di-
vided into two parts. The main part allow performing
intersection, calculating exact and approximate dis-
tances, and resolving contact determination queries
between two or more objects. These objects must
be convex and closed. However, the other part of
the library enables the conversion of non-convex and
opened models into convex hierarchies that can be
processed by the main part of the library. This library
can not work with non-2-manifold models or that con-
tain counter clockwise triangles. The features of the
algorithms are summarized in table 1.
3.1 Results
We have performed some tests to measure the effi-
ciency of the proposed strategies. These tests were
done with six models with a polygonal complexity in
the range from 7172 to 1085634 triangles (table 2).
Some of the models used(figure 1) have holes and are
not-2-manifold, therefore we can test the robustness
of each strategy. The measured parameters have been
the pre-processing time, the size of the data struc-
tures, and the time to determine the collision detec-
tion and to calculate the overlapping triangles. These
tests were performed on a 2,8 GHz Intel i7 PC with 4
GB of RAM.
Firstly, we have developed some tests to measure
the spatial decomposition performance. Both data
structures have been built under the same conditions:
A COMPARATIVE STUDY OF IMPLEMENTED COLLISION DETECTION STRATEGIES
487
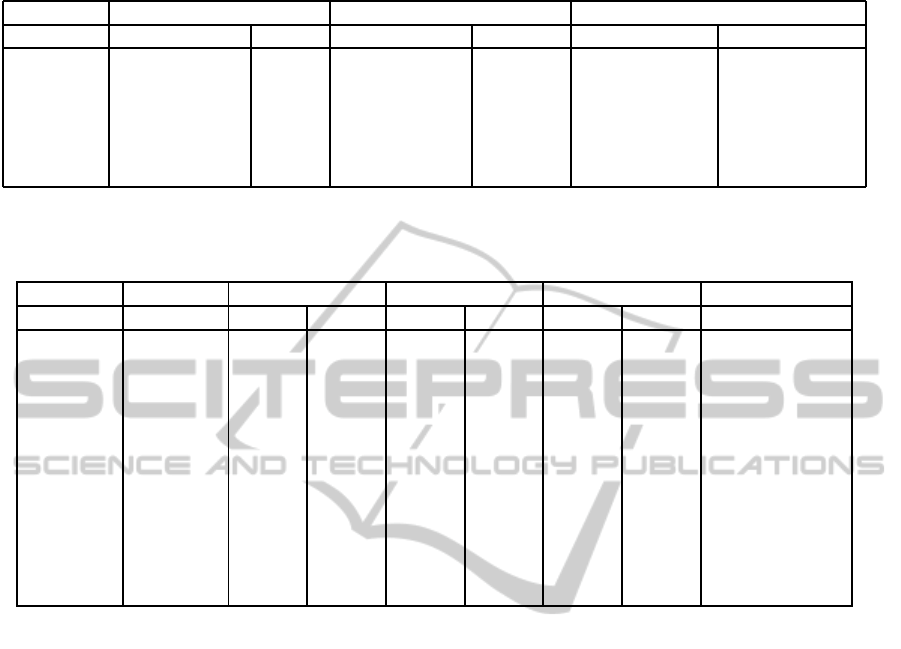
Table 3: Pre-processing time (s) and size (MB) of the proposed strategies.
Convex Hull PQP SWIFT++
Models Pre-processing Size Pre-processing Size Pre-processing Size
Horse 0,202 0,0252 0,045 2,8726 0,599 2,9544
Skull 3,8 0,6182 0,265 16,0216 8,094 20,6092
Bunny 4,3 0,2916 0,47 27,818 8,148 31,6224
Armadillo 15,7 0,3662 2,552 138,5654 380,121 162,3651
Dragon 42,5 0,4613 6,678 348,9311 Not 2-manifold Not 2-manifold
Buddha 130,4 1,1556 8,327 435,5262 Not 2-manifold Not 2-manifold
Table 4: Colision detection (C.D.) and overlapping triangles (O.T.) calculation (s) between object A and B using the proposed
strategies.
Octree Tetra-tree PQP Swift++
Model A Model B C.D. O.T. C.D. O.T. C.D. O.T. Collision
Buddha Horse 0,5807 0,6236 0,2161 0,409 0,0034 0,0104 Not-2-Manifold
Buddha Skull 1,8118 2,2317 0,2787 1,712 0,0076 0,017 Not-2-Manifold
Buddha Bunny 1,2058 1,7777 0,2481 1,1735 0,0102 0,041 Not-2-Manifold
Buddha Armadillo 2,026 4,5383 0,875 3,447 0,0106 0,4625 Not-2-Manifold
Dragon Horse 0,4144 0,3593 0,1444 0,307 0,0014 0,0043 Not-2-Manifold
Dragon Skull 0,8103 1,7643 0,2064 1,1583 0,0034 0,009 Not-2-Manifold
Dragon Bunny 0,6852 1,4197 0,2195 0,8823 0,0045 0,0145 Not-2-Manifold
Dragon Armadillo 1,1456 3,622 0,573 2,69 0,0087 0,0313 Not-2-Manifold
Armadillo Horse 0,0923 0,32 0,0892 0,22 0,0013 0,004 ≈ 0
Armadillo Skull 0,2605 1,5928 0,1108 1,184 0,0026 0,0054 ≈ 0
Armadillo Bunny 0,234 1,483 0,1673 0,9248 0,0033 0,009 ≈ 0
Armadillo Armadillo 0,588 3,3435 0,4418 3,207 0,0037 0,016 ≈ 0
same level and maximun threshold of triangles per
node. Nevertheless, it should be noted that the oc-
tree performs 8 subdivisions in each node and the
tretra-tree performs only 4, hence the number of oc-
tree nodes is higher. The results are shown in table 2.
In general, the tetra-tree has less pre-processing time,
but it needs more memory space.
The pre-processing time and size of the proposed
bounding volumes hierarchies have been measured.
Moreover, the convex hull has also been tested. The
size of each structure has been measured theoretically
because the real size depends on each machine and
compiler. Therefore, the calculated size is approxi-
mate.
In the case of spatial decompositions, size has
been calculated based on the theoretical size of each
node. In order to achieve this, the number of nodes
and their associated triangles have been measured. It
was considered that each node in the tetra-tree re-
quires 88 bytes: 16 bytes for children nodes (4 bytes
for each child pointer) and 72 bytes for tetra-cone ver-
tices (24 bytes per vertex). Since the centroid is a
common vertex for all the tetra-cones, it only needs to
store 3 vertices per tetra-cone. Additionally, the root
node requires 340 bytes: 4 bytes for the origin pointer,
8 bytes for the pointers to the lists of vertices and
triangles (4 bytes per pointer), 8 bytes for the num-
ber of vertices and triangles (4 bytes per number), 32
bytes for the eight initial tetra-cones (4 bytes for each
tetra-cone pointer), and 576 bytes for the vertices of
the initial tetra-cones (3 vertices per tetra-cone and
24 bytes per vertex). The octree requires 80 bytes per
node: 32 bytes for children nodes (4 bytes for each
children pointer) and 48 for the structure (2 vertices
and 3 coordinates per vertex). In this case, the root
node requires 72 bytes: 8 bytes for the pointers to the
lists of vertices and triangles, 8 bytes for the number
of vertices and triangles, 32 bytes for the initial oc-
tants (4 bytes for each octant), and 24 bytes for the
initial structure. In addition, both spatial decomposi-
tions need 4 bytes for each classified triangle.
PQP allows knowing the size of each structure at
runtime, hence this procedure has been used to calcu-
late the approximate size of the structure associated
with each model. It has not been possible to reach the
size of the data structures used by SWIFT++. How-
ever, this library allows exporting the hierarchies to a
file in order to facilitate reuse. We have used the size
of this file to approximate the size of the hierarchical
structure.
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
488

Figure 1: Models used for testing. From left to right and from top to bottom: horse, skull, bunny, armadillo, dragon and
buddha.
The results are shown in table 3. PQP is the op-
tion that requires less pre-processingtime, but it needs
a large amount of memory space. SWIFT++ also take
a long time and a lot of memory to build its struc-
ture. Moreover, it can not work with all of the pro-
posed models. The convex hull size is small because
its structure is very simple.
Table 4 shows the performance of each method to
calculate a collision detection and overlapping trian-
gles. SWIFT++ is the fastest method we are tested,
but it can not work with all the proposed models be-
cause some of them are non-2-manifold. Moreover,
it does not allow determining overlapping triangles.
PQP has a reasonable good performance and its main
advantage is that can work with all the proposed mod-
els. The spatial decomposition based methods do not
have good results. In both cases, spatial decomposi-
tions have been built under the same conditions as in
table 2.
Some tests to measure the performance of the
tetra-tree in an interactive environment are realized
in (Jim´enez et al., 2011). Models of different sizes
are used in order to perform these tests. Their results
show, in the same way as ours, that the tetra-tree re-
quire less pre-processing time that the octree, but it
needs a little more space in memory. The tests show
that the tetra-tree has some advantages with respect
to other approaches. Some of the main benefits are
that the tetra-tree enables the selection of inaccessible
parts without the use of extra algorithms and enable
an accurate level of detail.
3.2 GPU Optimization
Some of the proposed strategies obtain good results,
hence they can be applied to real-time interactive en-
vironments. However, some complex applications,
such us haptic interaction or complex deformations,
may require higher performance. In haptic interac-
tion, the refresh rate is 1Khz (Lin and Otaduy, 2008),
hence the collision detection should be calculated in
less than one millisecond. In order to achieve that, the
approaches shown could be improved and optimized
by using the GPU.
Spatial decompositions are not easily adaptable to
be used in parallel algorithms. However, in (Jim´enez
et al., 2009) a novel algorithm is presented. This algo-
rithm allows building and utilizing spatial decomposi-
tions in GPU. For that, they propose to use the geom-
etry shader. Each execution unit classifies a triangle
in a certain level, regardless of others. They propose
to use a n-sized texture for each level of the hierarchy,
where n is the number of triangles. Hence, the mesh
should be processed l times, where l is the level of the
hierarchy, in order to classify the mesh. In addition,
they propose to pre-calculate the spatial decomposi-
tion volume and codify it through a 2D texture.
The other libraries used do not have a GPU im-
plementation. However, in (Srungarapu et al., 2011)
the authors present a method to construct a convex
hull in GPU that could be adapted to build it in 3D.
This could be used in order to improvethe convex hull
strategy. Moreover, it would be interesting to consider
a GPU implementation of the other proposed strate-
gies.
4 CONCLUSIONS
In this work, we have presented some strategies to de-
tect collisions in interactive environments. Moreover,
some of the exposed methods allow performing other
A COMPARATIVE STUDY OF IMPLEMENTED COLLISION DETECTION STRATEGIES
489

interesting calculations, such us distances or nearest
points. On the one hand, SWIFT++ is the faster li-
brary we tested, but it requires a lot of pre-processing
time. On the other hand, PQP does not require much
pre-processing time and it is quite efficient at calcu-
lating collisions. Therefore, the use of each library
depends on the needs of each particular problem.
Since the octree and the tetra-tree has been im-
plemented without the use of any library, both spatial
decompositions, along with the Feito’s algorithm, can
be utilized to develop interactive systems that require
to implement extra functionality. Due to its robust-
ness, PQP is a good option in systems that work with
meshes that could be topologically not correct. This
is the case of systems that work with reconstructed
meshes, such us surgery simulators with medical im-
ages and scanner data. Moreover, PQP could be
a good solution for visualization applications, since
meshes used in such applications do not need to be
topologically correct. Finally, the SWIFT++ library
is suitable for real time environments that require a
good performance but that can ensure that the topol-
ogy of the models is correct. For that reason, this
library could be used for working with solid mod-
els which have been generated by mathematical and
boolean operations that conserve their topology. In
addition, this library could also be used in machining
simulation. In all three approaches, the implemented
systems must support a pre-processing step in which
construct the data-structures.
ACKNOWLEDGEMENTS
This work has been partially supported by the
Ministerio de Ciencia e Innovaci´on and the Euro-
pean Union (via ERDF funds) through the research
project TIN2011-25259 and by the University of Ja´en
through the research project UJA2010/13/08 spon-
sored by Caja Rural de Ja´en.
REFERENCES
Bergen, G. V. D. (2003). Collision Detection in Interactive
3D Environments. Elsevier.
Cameron, S. (1997). Enhancing gjk: computing mini-
mum and penetration distances between convex poly-
hedra. In Robotics and Automation, 1997. Proceend-
ings., 1997 IEEE Inter, pages 3112–3117.
Chen, H. and Huang, T. (1988). A survey of construction
and manipulation of octrees. Computer Vision, Graph-
ics, and Image Processing, 43:409–431.
Ehmann, S. and Lin, M. (2000). Accelerated proxim-
ity queries between convex polyhedra by multi-level
voronoi marching. In Intelligent Robots and Systems,
2000. (IROS 2000). Proceedings. 2000 IEEE/RSJ In-
ternational Conference on, volume 3, pages 2101 –
2106.
Ehmann, S. and Lin, M. (2001). Accurate and fast prox-
imity queries between polyhedra using convex sur-
face decomposition. Computer Graphics Forum,
20(3):500–511.
Feito, F. and Torres, J. (1997). Inclusion test for general
polyhedral. Computers & Graphics, 21(1):23–30.
Geiger, B. (2000). Real-time collision detection and re-
sponse for complex environments. In Computer
Graphics International, 2000. Proceedings, pages 105
– 113.
Gilbert, E., Johnson, D., and Keerthi, S. (1987). A fast pro-
cedure for computing the distance between complex
objects in three space. In Robotics and Automation.
Proceedings. 1987 IEEE International Conference on,
volume 4, pages 1883–1889.
Gottschalk, S., Lin, M., and Manocha, D. (1996). Obbtree:
a hierarchical structure for rapid interference detec-
tion. In Proceedings of the 23rd annual conference on
Computer graphics and interactive techniques, SIG-
GRAPH ’96, pages 171–180. ACM.
Jim´enez, J., Feito, F., Segura, R., and Og´ayar, C. (2006).
Particle oriented collision detection using simplicial
coverings and tetra-trees. Computer Graphics Forum,
25:53–68.
Jim´enez, J. and Segura, R. (2008). Collision detection be-
tween complex polyhedra. Computers & Graphics,
4(32).
Jim´enez, J. J., Feito, F. R., and Segura, R. J. (2011). Tetra-
trees properties in graphic interaction. Graphical
Models, 73(5):182 – 201.
Jim´enez, J. J., Mart´ınez, A., and Feito, F. R. (2009). Dise˜no
de descomposiciones espaciales jer´arquicas para mal-
las de tri´angulos utilizando geometry shaders. de-
sign of hierarchical space decompositions for triangle
meshes using geometry shaders. In CEIG09. Spanish
conference on Computer Graphics, pages 95–104.
Klosowski, J., Held, M., Mitchell, J., Sowizral, H., and
Zikan, K. (1998). Efficient collision detection using
bounding volume hierarchies of k-dops. Visualiza-
tion and Computer Graphics, IEEE Transactions on,
4(1):21–36.
Larsen, E., Gottschalk, S., Lin, M., and Manocha, D.
(1999). Fast proximity queries with swept sphere vol-
umes. Technical report, Department of Computer Sci-
ence, UNC Chapel Hill.
Lin, M. and Gottschalk, S. (1998). Collision detection be-
tween geometric models: A survey. In In Proc. of IMA
Conference on Mathematics of Surfaces, pages 37–56.
Lin, M. and Otaduy, M. (2008). Haptic Rendering: Foun-
dations, Algorithms and Applications. A. K. Peters
Ltd.
Srungarapu, S., Reddy, D., Kothapalli, K., and Narayanan,
P. (2011). Fast two dimensional convex hull on the
gpu. In Advanced Information Networking and Appli-
cations (WAINA), 2011 IEEE Workshops of Interna-
tional Conference on, pages 7–12.
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
490
