W-ENTROPY RANK

A Unified Reference for Search Engines

Li Weigang and Zheng Jianya

TransLab, Department of Computer Science, University of Brasilia-UnB, Brasilia, Brazil

Keywords: Baidu Weight, Information Theory, Sogou Rank, PageRank, W-entropy Rank.

Abstract: Baidu, Sogou and Google are three main utilized search engines in China reported by Chinese Internet Date

Centre (CNZZ) recently. During daily search in the Internet, it is easy to find that there are significant

differences among the search rank indexes such as Baidu weight, Sogou rank and PageRank. As a result, the

sequence of the search lists is totally different for a same keyword. On the other hand, some valuable

articles in web as blogs in ScienceNet.cn are ignored by Baidu, Sogou and others. It is impossible to unify

these ranking systems to a same level due to the business models from multi-enterprises. This paper studies

the difference of ranking indexes of these search engines by analyzing 4 kinds of 42 websites in China. With

the analyses of the correlation among these ranking indexes, averaged and weighted indexes, W-entropy

rank index using information theory is proposed as a search ranking reference. With the property analyses,

this new index demonstrates the ranking reality of Chinese websites. After the publication of this main idea

in our blog, Baidu and Sogou adjusted their ranking indexes of some websites, achieving a better match

with W-entropy rank index.

1 INTRODUCTION

According to the recent monthly report from

Chinese Internet Date Centre (CNZZ, 2011), Baidu,

Sogou and Google are three main search engines

with 93.50% using rate in China. At the same time,

some statistic results show that 70% of people use

search engines to find the product or service that

they want to buy; and 90% of web searchers never

make it to the second page of search results. This

means that to get a potential business and a better

propagation in the Internet, it is important to be

listed at the top of major search engines. In China,

there is no doubt, in Baidu, Sogou and Google.

Every search engine has proper criteria and

evaluation system to rank the feature of web pages,

such as Baidu weight (by Baidu search), Sogou rank

(by Sogou search), and PageRank (by Google search,

Brin and Page, 1998) and so on. However, the

difference of the ranking algorithms and criteria

systems makes the same web page have the different

importance values by above search engines. In some

especially situations, the Baidu weight and Sogou

rank are lower than PageRank for universities and

research institutions and Google has lower

PageRank than others for Chinese financial

institutions. As a result, the sequence of the search

results is totally different even for the same

keyword. Some valuable articles in web, such as

blog papers by some famous scientists in

ScienceNet.cn (ScienceNet, 2011) may be not well

classified and further propagated on the Internet,

even not be indexed by Baidu and Sogou search

engines.

In order to adjust the inequality of the inquiry

from different search engines, this paper firstly

analyzes the ranking indexes such as Baidu weight,

Sogou rank and PageRank for 42 websites from 4

categories institutions in China: Internet media,

universities and research institutions, financial

institutions and some enterprises to show the

problems. Then use statistical method to find out the

correlation between every two search engines, such

as Baidu weight with PageRank, etc. And further to

establish the mean index among these three ranks

and weighted index based on statistic result by

CNZZ. The paper also describes the model of W-

entropy rank using the information theory and the

application for the 42 websites mentioned above.

The W-entropy rank is proposed as a reference to

adjust the gap among the Baidu weight, Sogou rank

and PageRank. With the property analyses, this new

616

Weigang L. and Jianya Z..

W-ENTROPY RANK - A Uniﬁed Reference for Search Engines.

DOI: 10.5220/0003936306160624

In Proceedings of the 8th International Conference on Web Information Systems and Technologies (WEBIST-2012), pages 616-624

ISBN: 978-989-8565-08-2

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

index demonstrates the ranking reality of Chinese

websites. After the publication of our main idea in

our blog of ScienceNet.cn, Baidu and Sogou

adjusted their ranking indexes achieving a better

matching with the result of W-entropy rank index

and reality.

The paper is organized as following. Section 2

explains the problem of the heterogenic ranking

indexes of search engines in China. Section 3

analyzes the different search engines return the

different results for the same query keywords using

the example of a blog article in ScienceNet. Section

4 studies the correlation among the ranking indexes

from these search engines by comparing various

website samples. In section 5, the paper presents the

information theory briefly and proposes a new index

called W-entropy rank to unify the existed search

ranking indexes as a reference. And in section 6, it

analyzes the property of the new index to be used as

a reference for the search engines. The application

results of W-entropy Rank are illustrated in section 7

and the section 8 is the conclusion of the paper.

2 HETEROGENIC RANKING

INDEXES OF SEARCH

ENGINES

As mentioned by the report from CNZZ, in October

2011(CNZZ, 2011), Baidu search engine remained

in the top shot with a commanding 81.10% market

share in China, Sogou earned 7.52% share and the

third place Google had 5.49% share. This paper

takes these three most popular search engines to

study the ranking index, a measurement of

importance of the web pages.

Table 1 shows the rank indexes by the search

engines for some websites in China and there are

two rank values in the last columns: Averaged rank

is the average of rank indexes from these three

search engines. Another is Weighted rank, where

every search engine is assigned a different weight in

accordance of market share. Baidu is weighted as

81.10%, Google and Sogou both are weighted as

9.45%. The distribution of the weights is still a

research topic. It may use the Analytic Hierarchy

Process – AHP (Saaty, 1989) to further study the

effective weights to reflect the reality.

1) The website of Baidu gets 9/10 score from every

one of these three engines. For Google’s site, 8

score was weighted by Baidu, ranked 9 by

Sogou, and PageRank 10 by itself, so the

Averaged rank of Google is 9, but its Weighted

rank is 8.28. For Sogou’s site, the rank index

from both Baidu weight and Sogou rank is 9, its

PageRank is 8, the Averaged rank of Sogou is

8.33 and Weighted Rank is 8.81. These data

present the basic scenario of Chinese search

engines and the market share distribution.

2) From the collected data, Baidu weighted 4/10

score for the websites of both Zhejiang

University and Chinese Academy of Science

(CAS). Sogou rank is 6 for them. However,

Google’s PageRank for Zhejiang University is 9,

and for Chinese Academy of Science is 8. This

result shows the Baidu search engine classified

the websites of the most universities

unreasonable systematically till now.

3) There is also some inequality classification for

the web sites of financial institutions. For the

website of Industrial and Commercial Bank of

China – ICBC, its Sogou rank is 9; Baidu weight

is 8; Google’s PageRank is only 7. In an especial

case, Baidu just weighted the website of Unipay,

the biggest credit card company in China, as 2,

and 1 by Sogou rank. It should be mentioned

that, Unipay is the biggest credit card company

in China. This situation shows the importance to

develop a unify index system as a reference for

these search engines in China.

Table 1: Rank indexes of Baidu, Sogou, Google for related web sites (2011-11-14).

Website

URL Field Baidu

Weight

Sogou

Rank

Google PR Averaged

Rank

Weighted

Rank

Baidu baidu.com search 9 9 9 9 9

Google google.com search 8 9 10 9 8.28

Sogou sogou.com search 9 9 7 8.33 8.81

Zhejiang

zju.edu.cn education 4 6 9 6.33 4.66

CAS cas.cn science 4 6 8 6 4.57

ICBC icbc.com.cn financial 8 9 7 8 8

Unipay unionpay.com financial 2 1 7 3.33 2.38

W-ENTROPYRANK-AUnifiedReferenceforSearchEngines

617

3 DIFFERENT SEARCH

ENGINES, DIFFERENT RANKS

In this section, some propagation and search results

in the Internet are discussed concern to a blog article

of Shi Yigong, a famous scientist from Tsinghua

University. In September 9th, 2011, he published an

article “How to be an excellent PhD student?” (Shi,

2011) in his blog hosted by ScienceNet. Using the

title of the article as the keyword to search in Baidu,

Sogou and Google, there are some interesting results

to be analyzed:

1) The first three results listed in the first page of

Baidu search engine are respectively: a) the

article re-published by Baidu Online Library; b)

the article re-published by Douban online

community; c) the article re-published by

Dingxiang forum. This sequence basically is

ordered by the Baidu weight, a rank index of

Baidu to classify the importance of websites. The

website of both of Baidu Library and Douban

online community is with 9 of the Baidu weight

and Sogou rank; and the website of Dingxiang is

with 6. Even the version of the article was re-

published in Baidu Library by someone rather

than the original author, Baidu indexed very fast

and took the snapshot on September 14th.

Whereas the original version from the blog of

SicenceNet, was listed in 24th place on the third

page and didn’t take the snapshot until

November 13th.

2) In Sogou search engine, the first three results

were listed as: a) the article re-published by the

Sina iask site; b) the article re-published by

Baidu Online Library; c) the article published in

the 1000plan net. For Sina iask site, the Sogou

rank is 5, for Baidu Library and 1000plan, both

of them is 4. Although in the first 8 search pages

(with 80 results), all the links are totally with the

re-published version of the article, and there is

no exist the original version from ScienceNet. It

can be explain reasonable, Sogou ranked 2 for

the website of the blog of ScienceNet.

3) The results from Google search engine are: a) the

original version of the article in the blog of

ScienceNet; b) the related article “How to be a

good PhD student (continue)” (Shi, 2011) in the

ScienceNet; c) the article republished by Sina

iask site. Google classified ScienceNet as PR 9

and the blog of ScienceNet as 7. According to

this high ranking index, the original version and

the related article are certainly listed in the first

two lines by Google, see figure 1.

Figure 1: The search result of “How to be a good PhD

student” by Google.

Compare with the results of this example, it can

be found that the different ranking indexes are main

reason of the scenario of heterogenic search results.

The search engines of Baidu and Sogou focus on the

popular sites and Google gives more weight to the

innovation pages.

4 CORRELATION BETWEEN

DIFFERENT RANK INDEXES

As mentioned above, the different search engines

with different search reports. How about the relation

among the ranking criteria from the different search

engines? Correlation coefficient (R) (Pearson, 1896)

is used as an indicator to measure the relationship

among these indicators. The range of R is [-1, 1], the

abstract value of R bigger, the correlation between

these variables stronger, otherwise the correlation is

weaker. Usually when the |R| >0.8, it is considered

that these two variables have strong correlation.

Table 2 listed the ranking indexes from Baidu,

Sogou and Google for some websites of the Internet

media in China. The data were collected in Nov. 14,

2011.

The correlation is defined syntactical by 5 levels:

|R| between 0~0.2 is no correlation, 0.2~0.4 is little

correlation, 0.4~0.6 is ordinary correlation, 0.6~0.8

is fine correlation, 0.8~1.0 is linear correlation.

Table 3 shows the correlation among the ranking

indexes form Baidu, Sogou and Google search

engines. It is also analyzed the correlation among the

ranking indexes with the Averaged Rank and

Weighted Rank indexes. The |R| between Baidu

weight and Sogou rank is 0.0663, so there is no

correlation between the ranking indexes from these

two search engines; also they don’t have correlation

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

618

Table 2: The ranking indexes for some websites of the Internet media (2011-11-14).

Website URL

Baidu

Weight

Sogou

Rank

Google

PageRank

Averaged

Rank

Weighted

Rank

Baidu baidu.com 9 9 9 9 9

Sohu sohu.com 9 9 8 8.67 8.91

Sogou sogou.com 9 9 7 8.33 8.81

Google google.com 8 9 10 9 8.28

Sina sina.com 9 9 8 8.67 8.91

Tencent qq.com 10 9 8 9 9.72

Sina micro-blog weibo.com 9 1 8 6 8.15

Net Ease 163.com 9 9 8 8.67 8.91

Youku youku.com 10 8 8 8.67 8.62

Tianya tianya.cn 9 8 8 8.33 8.81

Douban douban.com 9 8 7 8 8.72

Mop mop.com 8 7 7 7.33 7.81

Table 3: The correlation analyses among the ranking indexes from Baidu, Sogou and Google.

Baidu Weight Sogou Rank PageRank Averaged Rank Weighted Rank

Baidu Weight - 0.0663 0.1768 0.2311 0.8978

Sogou Rank No - 0.1406 0.9329 0.4749

PageRank No no - 0.4085 0.0447

Averaged Rank Little Linear Ordinary - -

Weighted Rank Linear Ordinary No - -

Table 4: The ranking indexes for some websites of the education institutions (2011-11-14).

Website URL

Baidu

Weight

Sogou

Rank

Google

PageRank

Averaged

Rank

Weighted

Rank

Tsinghua U. tsinghua.edu.cn 5 7 9 7 5.57

Peking University pku.edu.cn 6 7 9 7.33 6.38

USTC ustc.edu.cn 5 5 8 6 5.28

Nanjing U. nju.edu.cn 6 5 9 6.67 6.19

Fudan University fudan.edu.cn 5 6 9 6.67 5.47

Zhejiang U. zju.edu.cn 4 6 9 6.33 4.66

SJTU sjtu.edu.cn 4 7 9 6.67 4.76

RUC ruc.edu.cn 5 6 8 6.33 5.38

Sun Yet-Sen U. sysu.edu.cn 6 5 8 6.33 6.09

CAS cas.cn 4 6 8 6 4.57

ScienceNet sciencenet.cn 6 5 9 6.67 5.38

1000plan 1000plan.org 3 4 7 4.67 3.47

Table 5: Correlations among three search engines.

Baidu Weight Sogou Rank PageRank Averaged

Rank

Weighted

Rank

Baidu Weight - 0.0709 0.4737 0.6947 0.9874

Sogou Rank No - 0.6285 0.7326 0.2204

PageRank Ordinary Fine - 0.8798 0.5890

Averaged Rank Fine Fine Linear - -

Weighted Rank Linear Little Ordinary - -

with PageRank of Google, the |R| values are 0.1768

and 0.1406 respectively. Baidu weight has little

correlation with the Averaged Rank, but has linear

correlation with the Weighted Rank, obviously the

reason is that the weight of the ranking index of

Baidu is 81.1% when calculation the Weighted Rank

W-ENTROPYRANK-AUnifiedReferenceforSearchEngines

619

value. Sogou rank has linear correlation with the

Averaged Rank value and ordinary correlation with

the Weighted Rank value; Google has ordinary

correlation with Averaged Rank value and has no

correlation with the Weighted Rank value.

Table 4 listed the ranking indexes from Baidu,

Sogou and Google for some websites of the

education institutions in China. The data were

collected in Nov. 14, 2011. In table 4, USTC is the

abbreviation of the University of Science and

Technology, and SJTU is the Shanghai Jiaotong

University. And RUC is the People’s University.

Table 5 presents the analyses of the correlation

among the ranking indexes from Baidu, Sogou and

Google for the websites of some Chinese education

institutions. Baidu weight has no correlation with

Sogou rank, the |R| between them is 0.0709; it has

ordinary correlation with Google PageRank

(0.4737), fine correlation with Averaged

rank value (0.6947) and linear correlation with

Weight rank value. Sogou rank has ordinary

correlations with PageRank of Google and Averaged

rank, little correlation with the Weighted rank value.

Google PageRank has linear correlation with

Average rank value and fine correlation with

Weighted rank value.

Analyzing above studies, some interesting points

should be mentioned:

1) Heterogenic sequences of presentation the search

results of the same keyword from the different

search engines should be noted in Chinese

Internet search scenario. The main reason is that

every search engine has its own criterions and

algorithms to determine the rank of web pages.

This is a difficulty factor in the Search Engine

Optimization.

2) The Averaged rank indexes of Tencent, Baidu

and Google are 9, but distribution manner of

ranking index from the every search engine is

different. For example, for Tencent,

its Baidu weight is 10, its Sogou Rank is 9 and

its Google PageRank is 8. The Weighted rank

index can distinguish this difference.

3) According to the correlation analyses, in

Averaged rank case, Baidu weight has linear

correlation with the Averaged rank, and Sogou

rank too. Google PageRank has little correlation

with Averaged rank. In Weighted rank case, only

the Baidu weight has linear correlation with

Weighted rank index. Sogou rank has fine

correlation with Weighted rank value and Google

PageRank has no correlation with it. So, there is

a necessary to develop a new ranking index with

the advantage from both of Averaged rank and

Weighted rank.

5 INFORMATION THEORY AND

THE DEFINITION OF

W-ENTROPY RANK

The information theory is introduced firstly in this

section. Based on this theory, W-entropy rank is

defined.

5.1 Brief Introduction of Information

Theory

The concept of Shannon's entropy (Shannon, 1948)

is the central role of information theory sometimes

referred as a measurement of uncertainty. Let X be a

discrete random variable taking a finite number of

possible values x

, x

…x

with probabilities p

…p

respectively such that Δn = {P = (p

, p

…p

)

: p

≥0, ∑ p

= 1, i = 1, 2…n}. Let h be a function

defined on the interval (0, 1] and h(p) be interpreted

as the uncertainty associated with the event X = x

, i

= 1, 2…n. For each n, a function H

, p

…p

) is

defined as the average uncertainty associated with

the event {X = x

}, given by

∑

iinn

phppppH

,,2,1

)(*)...(

(1)

Let H

:Δn → IR (n≥2) be a function satisfying the

following axioms:

1) H

, p

… p

) is a continuous function of p Є

[0, 1].

2) H

, p

… p

) is a symmetric function of its

arguments.

3) H

, p

… p

) = H

n-1

, p

… p

) + (p

)*H

/( p

+ p

), p

/( p

+ p

) ), p

+ p

> 0.

Then H

, p

…p

) is the formula as Shannon

defined:

∑

−=

binn

pCpppH

,,2,1

log)...(

(2)

Where C > 0, b > 1, with 0*log

0 = 0.

Weigang presented a practical application of the

entropy, where the entropy of information was

applied to measure the degree of disorder and an

application algorithm was proposed (Weigang,

1988), also adopted this theory to measure the

influence of individual among the different social

networks (Weigang et al., 2011a).

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

620

5.2 Definition of W-entropy Rank

Suppose a ranking index for a web page is P

, j =

1...n, there are n these indexes from related search

engines. The weights of these indexes are {a

a2...a

}, ∑a

=1, which are selected as 1/n for every

search engines as mentioned in section 4. Because

the ranking index is usually divided in 10 levels, so

there is p

= P

/10.

Then the Averaged rank index of this web page is:

∑

pam

(3)

The Averaged rank is a very simple and intuitive

method to present the unified rank index for a web

page. As discussed in section 4, it cannot identify the

difference cases between the distribution of rank

indexes in 10, 9, 8, and in 9, 9, 9. The entropy

concept of information theory can be employed to

quantify this distribution. Firstly, there is a

transformation for p

to q

)1/( += npq

j=1,2…n

(4)

∑

−=

)1(

(5)

Where q

presents a numeric value of the

information of j

ranking index from j

engine. On the other hand, q

(n+1)

is a percent that

presents an absence of information of all n ranking

indexes of the related search engines. The entropy is

defined as a correction coefficient to reflect the

distribution of the ranking indexes of these related

search engines, in briefly distribution coefficient:

∑

−=

11,,2,1

log)...(

jnjn

qqqqqh

(6)

Based on the formulas (3) and (6), W-entropy

Rank, a new index to class the importance of a web

page can be defined as:

W-entropy Rank = h * m (7)

In order to simplify this formula for application

purposes, the value from formula (7) was scaled in

relation to maximum W-entropy Rank, and

multiplied by 100, which results in the following

equation:

max

relative

W entropy Rank

(8)

Generally, the Relative W-entropy rank index is

simply presented as W-entropy rank.

6 THE PROPERTY ANALYSIS OF

W-ENTROPY RANK

As calculated in equation (6), the distribution

coefficient for imbalance during the transmission of

information is defined as entropy of information

(Weigang et al., 2011b). This coefficient, h, must

present the following attributes: when all the

elements, q

, j=1,2…n, are equal to 1, it means that

the information of this individual is being

transmitted evenly among social networks, so the

distribution coefficient is set to 1. On the other hand,

when all the terms, q

, j=1,2…n, are equal to 0, it

means that transmission is uneven, therefore the

distribution coefficient is set equal to 0. The value of

the elements range from 0 to 1, thus the distribution

coefficient value also varies between 0 and 1.

To verify the validity and effectiveness of the

modified coefficient h, the following parameters

were used: n = 3 and six sets of data were selected:

Set1: p

[0, 0.1, 0.2...1], p

[0, 0, 0...0], p

[0, 0, 0...0]

Set2: p

[1, 1, 1...1], p

[0, 0.1, 0.2...1], p

[0, 0, 0...0]

Set3: p

[1, 1, 1...1], p

[0, 0.1, 0.2...1]

Set4: p

[1, 0.9, 0.8 ...0], p

[1, 1, 1...1], p

[1, 1, 1...1]

Set5: p

[0, 0, 0...0], p

[1, 0.9, 0.8 ...0], p

[1, 1, 1...1]

Set6: p

[0, 0, 0...0], p

[1, 0.9, 0.8 ...0]

Based on the data, it can be seen that in the first

three sets of data, the trend of the imbalance during

transmission went from 0 to 1, so the distribution

coefficient h also assumed a value that ranges from

0 to 1. The last three sets of data shown were used to

illustrate an opposite scenario, where the trend went

from 1 to 0 and the distribution coefficient also

ranged from 1 to 0. Thus, h*w and the W-entropy

rank will have the same monotonic trend. Figure 2 is

a plot of h as a function of w. These results illustrate

the property of generality of the distribution

coefficient.

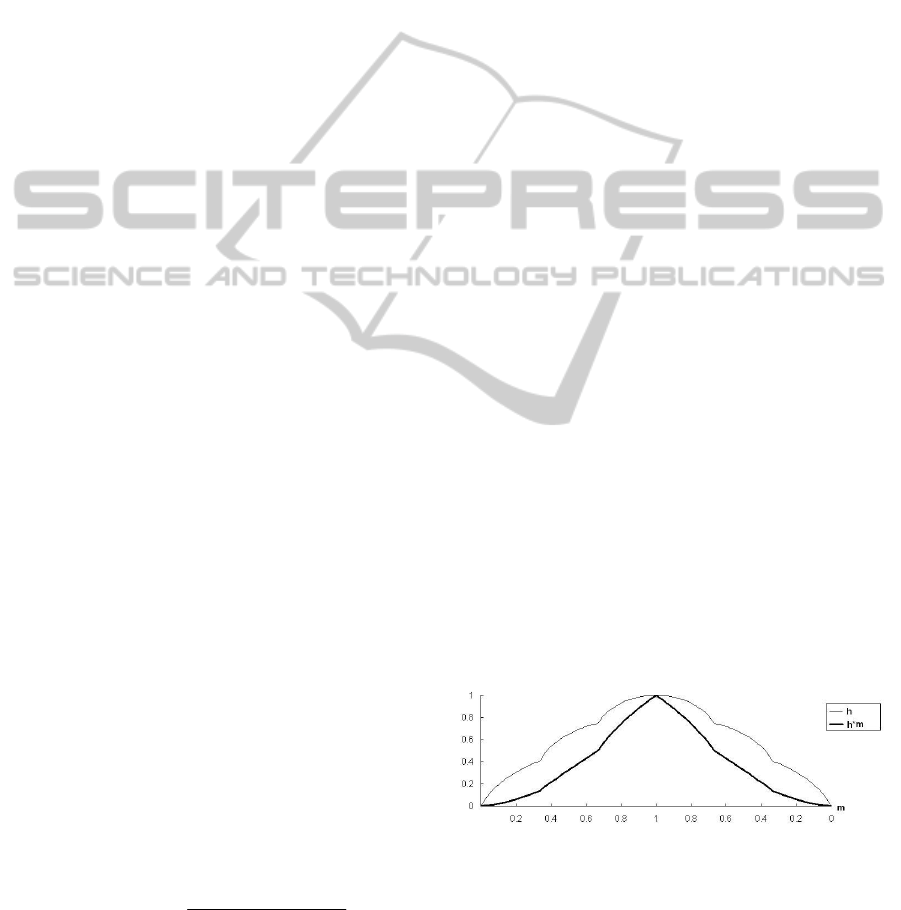
Figure 2: A graphic of Entropy and h and h*m with m.

different for these lines, the values of the distribution

coefficient h = 0.4056 and h*m = 0.1352 are the

same because of symmetry in m. If the values of

, p

} are {0.3333,0.3333,0.3333}, then the

value of m is also 0.3333; in this case, h = 0.6037

and h*m = 0.2012, which are greater than the values

W-ENTROPYRANK-AUnifiedReferenceforSearchEngines

621

for the third and eleventh line. This result further

supports the validity of the modified coefficient

method.

7 APPLICATION OF

W-ENTROPY RANK

This section presents the application of W-Entropy

rank to the web sites of the Internet media and

education institutions of China. There is some

difference of the ranking indexes of Baidu, Sogou

between tables 2 and 7 (4 and 8 too) because the

companies of these search engines changed the

ranking indexes during this period.

7.1 W-entropy Rank for Some

Websites of the Internet Media

Table 6 shows the W-entropy rank indexes for some

websites of the Internet media in China. For the

website of Baidu, its ranking index is 9/10 by Baidu,

Sogou and Google. The Averaged rank index is 9

too. The distribution coefficient h is 0.9863, the

absolute W-entropy rank index is 8.88. This is the

largest value in this moment, so, the relative W-

entropy rank index of Baidu is defined as 100.

In case of Google, its website is classified by

Baidu as 8, Sogou as 9 and proper as 10, The

Averaged rank index is 9 too. The distribution

coefficient h is 0.9829, the absolute W-entropy rank

index is 8.85. According to Baidu, the relative W-

entropy rank index of Google is defined as 99.78.

As in table 6, for websites of Tencent and

Youku, Baidu changed the weight for them from 10

to 9, which is the maximum Baidu weight value in

China now. So, the relative W-entropy rank index of

Tencent together with Sina, NetEase and Sohu is

95.48, Youku is 90.91 together with Tianya.

In an especial case, Baidu re-classified Unipay’s

website from 2 to 4, the adjustment reflected the

affection of our proposal. As the result, the relative

W-entropy rank index of Unipay is defined as 28.41.

7.2 W-entropy Rank for Some

Websites of Education Institutions

As an indicial study in table 4, Baidu and Sogou

classified the websites of education institutions with

lower indexes. In the later of November, these

search engines changed the rank indexes for these

websites. As presented in table 7, the Baidu weight

of the websites of Shanghai Jiaotong University and

Zhejiang University were re-classified from 2 to 4.

And the websites of Tsinghua University, People’s

University of China, Nanjing University, Sun Yat-

sen University and University of Science and

Technology of China ware modified from 5 to 6. For

Chinese Academy of Science, its Baidu weight was

also increased from 4 to 5.

As the results, in the Shanghai Jiaotong

University, Peking University and Tsinghua

University, their websites were classified by Baidu

as 6, Sogou as 7 and Google as 9, The Averaged

rank index is 7.33. The distribution coefficient h is

0.9309, the absolute W-entropy rank index is 6.83.

According to Baidu, the relative W-entropy rank

index of them is defined as 76.28.

The Fudan University, Nanjing University and

Zhejiang University shared fourth place with the W-

Entropy rank index 71.33. Sun Yat-sen University,

Chinese Academy of Science, University of Science

and Technology of China, ScienceNet are also listed

in the same level with the W-Entropy rank index

more or less 62.

Comparing the results in table 7 and the Internet

traffic records of Alexa (Alexa, 2011), the rank

sequence of the websites is listed as the Shanghai

Jiaotong Unviersity, Fudan University, ScienceNet,

Tsinghua University, Peking University, Nanjing

University, and Zhejiang University. This means

that, probably, Baidu and Sogou search engines

adjusted the classification for this institutions using

W-entropy rank as a reference.

7.3 Correlation Analyses of W-entropy

Rank with Others

In this section, 42 websites from some Internet

media, education, research, finance institutions and

telecommunication enterprises were selected to

analyze the correlation between the W-entropy rank

index and the rank indexes from every individual

search engine. The indicial results are presented in

table 8.

1) With the comparison, the correlation between W-

entropy rank index and Baidu weight is 0.8657,

i.e, linear correlation. For Sogou rank, the

correlation coefficient is 0.8647 and also as

linear correlation. For the PageRank of Google,

the correlation coefficient is 0.3402, even it is

with little correlation, but is still better than

PageRank with Weighted rank. This result

reduces the gap between the PageRank with

other two ranking indexes.

2) Comparing the correlation study among the

Baidu weight, Sogou rank and Google PageRank

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

622

Table 6: W-entropy rank for some websites of the Internet media (2011-12-01).

Website URL

Baidu

Weight

Sogou

Rank

Google

Averaged

Rank

W-Entropy

Rank

Baidu baidu.com 9 9 9 9 100

Google google.com 8 9 10 9 99.78

Tencent qq.com 10/9 9 8 8.67 95.48

Sina sina.com 9 9 8 8.67 95.48

NetEase

163.com

9 9 8 8.67 95.48

Sohu sohu.com 9 9 8 8.67 95.48

Youku

youku.com

10/9 8 8 8.33 90.91

Tianya tianya.cn 9 8 8 8.33 90.91

Sogou sogou.com 9 9 7 8.33 90.70

Douban douban.com 9 8 7 8 86.10

Mop mop.com 8/9 7 7 7.67 81.79

Sina weibo weibo.com 9 1 8 6 52.40

Visa China visa.com.cn 1 5 6 4 28.71

China-Unipay unionpay.com 2/4 1 7 4 28.41

Table 7: W-entropy rank for some websites of education institutions (2011-12-01).

Website URL

Baidu

Weight

Sogou

Rank

Google

Averaged

Rank

W-Entropy

Rank

SJTU sjtu.edu.cn 4/6 7 9 7.33

76.28

Tsinghua U. tsinghua.edu.cn 5/6 7 9 7.33 76.28

Peking U. pku.edu.cn 6 7 9 7.33 76.28

Fudan University fudan.edu.cn 5/6 6 9 7

71.33

Nanjing U. nju.edu.cn 6/6 5/6 9 7

71.33

Zhejiang U. zju.edu.cn 4/6 6 9 7

71.33

People’s university ruc.edu.cn 5/6 6 8 6.67

66.81

CAS cas.cn 4/5 6 8 6.33 61.78

Sun Yet-sen U. sysu.edu.cn 6/6 5 8 6.33

61.78

USCT ustc.edu.cn 5/6 5 8 6.33

61.78

Science Net sciencenet.cn 6/5 5 9 6.33 61.22

1000plan 1000plan.org 3 4 7 4.67

38.15

Table 8: Correlation analyses of W-Entropy rank with the indexes of Baidu, Sogou and Google.

Baidu

Weight

Sogou

Rank

PageRank Averaged

Rank

Weighted

Rank

W-entropy

rank

Baidu Weight - 0.5648 0.1530 0.8796 0.9957 0.8657

Sogou Rank Ordinary - 0.1044 0.8438 0.6297 0.8647

PageRank No No - 0.3442 0.1968 0.3402

Averaged Rank Linear Linear Little -

Weighted Rank Linear Fine No - - -

W-entropy Rank Linear Linear Little - - -

The average of correlation coefficients between each search

engine and different rank value

0.6956 0.6074 0.6902

with the Average rank, Weighted rank and W-

entropy rank in table 8. The sum of the column

of the correlation coefficient of Average rank is

0.6956, the sum of the column of W-entropy

rank is 0.6094 and the Weighted rank is 0.6074,

this result shows that the W-entropy rank index

has a better presentation.

3) The W-entropy rank index is developed to

synchronize the information distribution of the

ranking indexes from the different search

engines. For example, in case of the websites of

Baidu and Tencent, both of them get 9 in

Average rank, but Baidu is also with a better

distribution of the classification: 9, 9, and 9 by

W-ENTROPYRANK-AUnifiedReferenceforSearchEngines

623

Baidu, Sogou and Google. As the result, the

distribution coefficient h is 0.9863, the absolute

W-entropy rank index is 8.88, and, the relative

W-entropy rank index of Baidu is 100.

Otherwise, in case of Google, the ranking

indexes are classified as 8, 9 and 10, the

distribution coefficient is 0.9829, so W-entropy

rank index is 99.78, lesser than Baidu.

8 CONCLUSIONS

As the national Internet search engines, Baidu,

Sogou and Soso take the main market share in

China. There is still a space for Google search too.

In order to adjust the gaps among the Baidu weight,

Sogou rank and PageRank of Google and other

search engines, a new concept, W-entropy rank is

proposed as a reference. This index unifies the rank

indexes from above research engines to smooth the

gaps among them. It is also better than simple use

the averaged rank because of using the entropy

concept of the information theory to reflect the

distribution of the information from different

ranking indexes of the related platforms. This index

unifies the rank indexes from above research engines

to smooth the gaps among them. It is also better than

simple use the averaged rank because of using the

entropy theory to reflect the distribution of the

information from different ranking indexes of the

related platforms.

W-entropy rank can also be used as to rank the

websites according to their importance. Based on the

study of 42 websites over 4 kinds of the sectors such

as Internet media, education/research, finance

institutions and telecommunication enterprises, the

sequence of these websites according the W-entropy

rank is well listed comparing with the Internet traffic

rank list by Alexa.

It should be mentioned that, the W-entropy rank

is not proposed to substitute the existed ranking

indexes, but just to be a reference for all search

engines in China. After the publication the main idea

in our blog in ScienceNet.cn about this reference,

Baidu and Sogou even changed their ranking

indexes quickly, especially for education and

research institutions.

The further study of this research is to develop

an automated system to produce frequently a W-

entropy rank list to cover the important websites in

China even worldwide to establish a public domain

for reference to any kinds of the users, especially,

search engines. It is very important with a

democracy and quality in the website ranking by any

search engine over the Internet.

REFERENCES

CNZZ (Chinese Internet Date Centre), Monthly report of

the using rate of Chinese Internet search engines,

2011. http://data.cnzz.com/main.php?s=engine

Brin, S., Page, L. 1998. The anatomy of a large-scale

hyper-textual web search engine. Computer Networks

and ISDN Syst. 30 (April 1998), 107-117.

ScientNet, 2011. http://www.sciencenet.cn

Saaty, Thomas; Alexander, Joyce, 1989. Conflict

Resolution: The Analytic Hierarchy Process. New

York, New York: Praeger.

Shi Yigong, 2011, How to be an excellent PhD student.

http://bbs.sciencenet.cn/home.php?mod=space&uid=4

6212&do=blog&id=484416.

Pearson, K., 1896. Mathematical contributions to the

theory of evolution, III: regression, heredity and

panmixia. Philos. Trans. Roy. Soc. London Ser. A 187

253–318.

Shannon, C. E., 1948, A Mathematical Theory of

Communication. Bell System Technical Journal, Vol.

27, pp. 379–423, 623–656.

Weigang, L., 1988. An Algorithm for Negative Entropy-

The Sequence of the Complex System Structure.

Systems Engineering Theory & Practice, 8(4), 15-22..

Weigang, L., Jianya, Z., Daniel, L., 2011a. W-entropy

Index: the Impact of Members on Social Networks. In

the Proceedings of the Web Information Systems and

Mining - WISM 2011, Taiyuan, China, Part I, LNCS

6987, 226-233.

Weigang, L., Jianya, Z., Daniel, L., 2011b. Analysis of W-

entropy Index: the Impact of Members on Social

Networks. In the proceedings of IADIS International

Conference WWW/INTERNET, Rio de Janeiro,

Brazil, 171-178. Best Paper Award.

Alexa, Internet Information website, 2011, http://

alexa.com/.

WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies

624