MIXED-INITIATIVE SCHEDULING OF TASKS
IN USER COLLABORATION
L. Ardissono, G. Petrone, G. Torta and M. Segnan
Dipartimento di Informatica, Universit`a di Torino, Corso Svizzera 185, Torino, Italy
Keywords:
Scheduling User Tasks, Collaboration Support, Mixed-initiative Interaction, Temporal Reasoning.
Abstract:
This paper describes an intelligent, mixed-initiative scheduler which supports users in the organization and re-
vision of their calendars, helping them to allocate personal and shared activities involving other collaborators.
Our scheduler exploits well-known temporal reasoning techniques to suggest complete schedules, as well as
to guide the user in the exploration of the possible changes to the timing of tasks, in order to enable her/him to
modify the calendar in an informed way. We have integrated our scheduler into a Collaborative Task Manager
service supporting the management of projects and distributed tasks.
1 INTRODUCTION
The increasing adoption of online calendars for orga-
nizing people’s schedules and their availability “in the
cloud” offer excellent opportunities for the develop-
ment of services holistically supporting the manage-
ment of personal and shared activities at home and
at the workplace. In fact, the ubiquitous availability
of such tools enables users to manage their work and
personal schedules, providing a user-centered per-
spective of their commitments. However, in order to
help users to organize their activity contexts, which
might involve different groups of people, an explicit
task scheduling support is needed, which analyzes the
schedules of the involved users and suggests feasible
time intervals for the execution of activities.
As a first step towards addressing this issue, we
propose an intelligent, mixed-initiativescheduler sup-
porting the generation and revisionof the user’scalen-
dar, given her/his commitments and those of the other
actors involved in the shared activities. The main fea-
ture of our scheduler is its mixed-initiative, conser-
vative support: besides the generation of complete
schedule proposals, our system helps the user to re-
vise a schedule by suggesting alternative allocations
of the tasks to be moved. The scheduler proposes
conservative changes to the user’s calendar in order to
maintain previous commitments as originally planned
or with minor temporal shifts; in turn, the user can
choose the preferred one and apply it. The calendars
of all the involved actors are updated accordingly.
Our scheduler is based on the exploitation of Tem-
poral Constraint Satisfaction Problems (TCSP) tech-
niques, used to generate safe full schedule proposals
as well as to present all of the admissible intervals for
the placement of specific tasks.
The rest of this paper is organized as follows: Sec-
tion 2 presents a running example describing a usage
scenario for our mixed-initiative scheduler. Section 3
describes the services offered by the system and its
underlying model. Section 4 explains the technical
details behind our proposal. Section 5 presents some
related work and Section 6 concludes the paper.
2 RUNNING EXAMPLE
We describe the services offered by our mixed-
initiative scheduler by means of a running example.
Let’s suppose that, as new tasks are assigned to a user
U, they are placed within free spots in the user’s cal-
endar, either manually by U or by the mixed-initiative
scheduler, without involving U in the decision. This
process is only adequate as long as new tasks can be
scheduled without affecting the other tasks that are al-
ready in the calendar.
Figure 1 shows the user interface of our mixed-
initiative scheduler and displays a possible calendar
where we assume that the tasks have been placed in
this way. The placement of tasks satisfies some con-
straints given by the user: for example, the Library
meeting cannot take place at lunch time (13.00 to
14.00)
1
or after 17.00, and must take place before Th-
342
Ardissono L., Petrone G., Torta G. and Segnan M..
MIXED-INITIATIVE SCHEDULING OF TASKS IN USER COLLABORATION.
DOI: 10.5220/0003937903420351
In Proceedings of the 8th International Conference on Web Information Systems and Technologies (WEBIST-2012), pages 342-351
ISBN: 978-989-8565-08-2
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

ursday 11.00. Moreover, the Phd meeting and the
phone call must take place on Wednesday, before
20.00, and the phone call must take place after the
Phd meeting, e.g., because the user has to talk to Mr.
Smith about a decision taken in the meeting.
Let’s assume that a new task arrives (e.g., meet-
ing the plumber for fixing a leaking sink), that takes 3
hours and has to be done on Wednesday before 18.00.
It is easy to see that there is no free spot in the calen-
dar where the new task can be placed. Then, the user
can ask for the help of the mixed-initiative scheduler:
• The user can ask when the task can be allocated;
the scheduler replies that it could start at 13.00,
14.00 or 15.00, since this would only require to
anticipate or postpone the afternoon tasks, with-
out affecting the order of the current ones. Indeed,
if the new task is placed at 13.00 or 14.00, it is
sufficient to delay the Ph.d meeting and the phone
call. Otherwise, if it is placed at 15.00, a solution
can be found by anticipating the Ph.d meeting and
deferring the phone call, and slipping the new task
between them.
• If the user is not satisfied with meeting the
plumber in the afternoon, (s)he can try to move
the Library meeting to make room for the new
task. For this purpose, the user points to the Li-
brary meeting task and asks the temporal reasoner
again for help. The reasoner replies that, consid-
ering only the user’s tasks in the current schedule,
the Library meeting can be moved to Wednesday
at 8.00, 9.00, 14.00, 15.00 or to Thursday either at
8.00 or at 9.00 (in which case, the write paper task
should be anticipated to Wednesday afternoon).
If, after exploring several possibilities with the
help of the scheduler, the user is still unsatisfied, (s)he
can request a brand new schedule. However, this may
cause many of the other tasks to change their times
and their relative order.
3 MIXED-INITIATIVE TASK
SCHEDULING
Our scheduler is integrated in a Collaborative Task
Manager (CTM) service (Ardissono et al., 2011;
Ardissono et al., 2012) that supports distributed col-
laboration by enabling users to synchronize with each
other in the execution of shared activities.
1
We use 24-hours notation so that, e.g. 13.00 and 14.00
stand respectively for 1pm and 2pm.
3.1 The Collaborative Task Manager
The CTM manages task nets that regulate the execu-
tion of complex activities, denoted as activity frames,
possibly decomposed in simpler tasks which can be
organized in patterns typical of workflow nets; e.g.,
sequence, parallel split, exclusive choice, synchro-
nization, simple merge, etc. (van der Aalst et al.,
2008). Figure 2 shows the user interface of the CTM
for the visualization of an activity frame: the CTM
visualizes the task net by coloring nodes on the basis
of their state. By clicking on a specific node, the user
can view the details of the represented task.
Within an activity frame, a task is modeled by
specifying various types of information, among which
the involved actors, the task state (disabled, enabled,
done), the expected duration, the task deadline (if
any) and the dependencies on other tasks. For in-
stance, in the activity frame of Figure 2, T3 is alter-
native to T2 and is enabled only after T1 is done. Ac-
tivity frames can also include simpler “to dos”, repre-
senting elementary tasks that the user wants to sched-
ule, even though they do not have a precise deadline
or structure. Overall, the CTM is based on Allen’s
Getting Things Done model for the organization of
human activity (Allen, 2003).
Using the user interface of the CTM, the actors
involved in an activity frame can manage their tasks
and “to dos”: as the user interface is web-based, they
can monitor the evolution of a collaboration on a stan-
dard web browser. Moreover, the CTM supports user
awareness by means of a notification service that in-
forms users about relevant events, such as the enable-
ment of a task (Ardissono and Bosio, 2012).
The CTM alone enables users to carry out activ-
ities according to the dependencies specified in the
task net. However, it does not help them to decide at
which time exactly they haveto, or can, performa par-
ticular task because it is not integrated with the actors’
calendars. The role of our mixed-initiative scheduler
is thus that of extending the CTM capabilities, help-
ing users to plan their activities in advance, but also
to react to unexpected events, such as changes in task
deadlines, or the occurrence of new commitments.
3.2 Our Mixed-initiative Scheduler
3.2.1 Features
The main requirements driving the design of our
scheduler are the following:
• Safe Scheduling: the proposed solutions must be
consistent with the constraints imposed on the
MIXED-INITIATIVESCHEDULINGOFTASKSINUSERCOLLABORATION
343

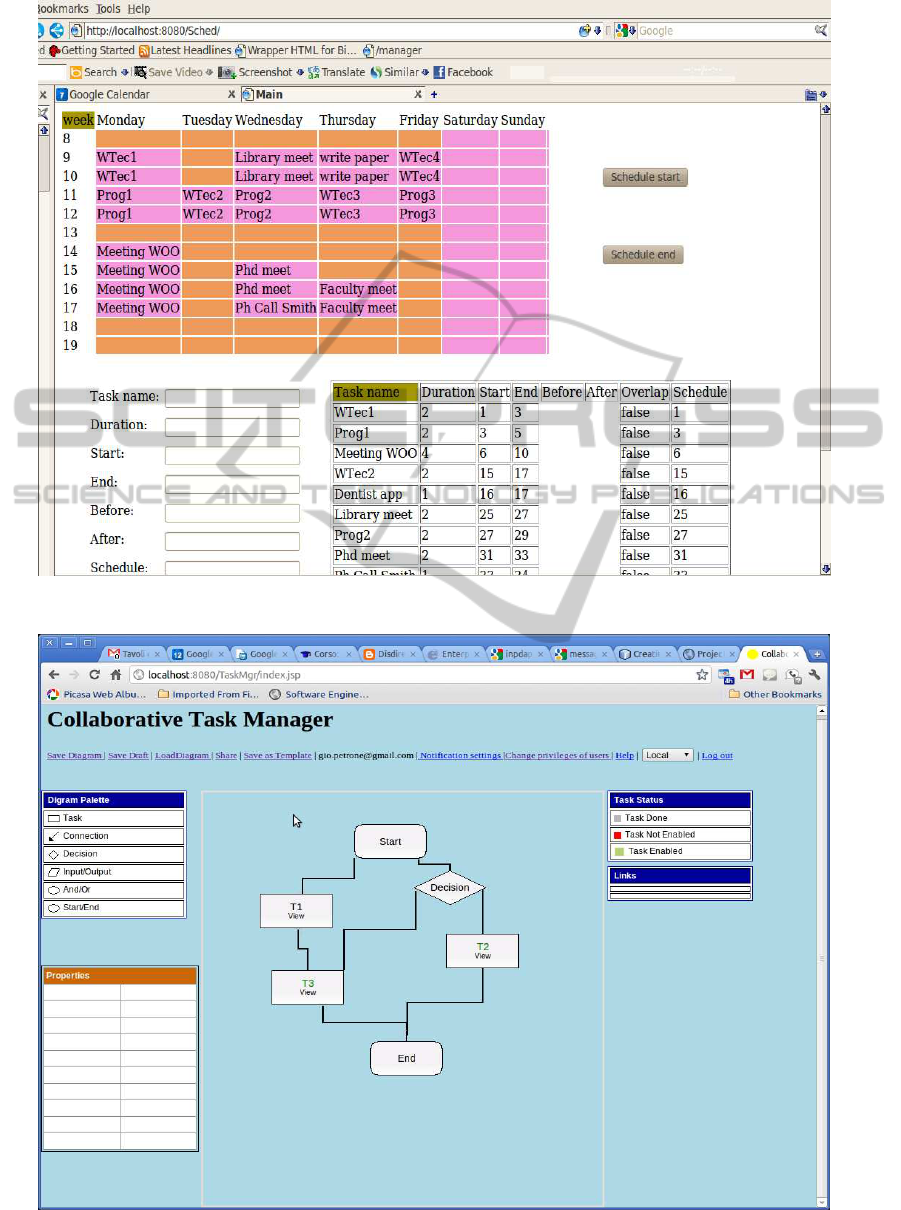
Figure 1: Visualization of a user’s schedule (week).
Figure 2: User interface of the CTM.
WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies
344

tasks in the user’s calendar and with the commit-
ments of the other involved actors; i.e., the mixed-
initiative scheduler must propose task allocations
that are feasible for all the participants.
• Mixed-initiative: if the user wants to inspect the
space of possible solutions, e.g., to allocate a new
task, or to move a task in the calendar, the sched-
uler has to visualize the admissible time slots for
the task (if any), so that the user can select the pre-
ferred schedule modification. In other words, the
user has an active role in guiding the scheduler’s
operations rather than being only responsible for
accepting or rejecting the proposed solutions.
• Collaboration Support: tasks are scheduled for all
the involved actors, taking into account their cal-
endars and the deadlines of their other commit-
ments.
• Conservativeness: unless the user requests a
new schedule, the mixed-initiative scheduler must
search for solutions that are as conservative as
possible with respect to the existing commitments
in order to avoid a complete reorganization of the
actors’ daily schedules.
As described in section 3.1, the Collaborative Task
Manager enables the user to define the tasks to be per-
formed by specifying their actors, duration, deadline,
and other types of information. Even though some
tasks have a fixed starting time, e.g., meetings, other
ones can be scheduled in alternative ways and there is
a safe starting time window which spans from the in-
stant of time when they are enabled (earliest starting
time) until the very last minute they have to be started
to meet their deadline. In order to safely schedule a
task, it has to be allocated within its safe starting time
window. However, the specific allocation is not by it-
self a hard constraint to be met and can be modified
for re-scheduling purposes. We thus model two main
types of information: the basic constraints of tasks,
which have to be met in any schedule proposal, and
the specific configuration of a calendar, which repre-
sents the user’s current decisions about how to orga-
nize the activities, but can be revised. The represen-
tation of tasks, and the temporal reasoning approach
adopted in our work, reflect this idea.
As discussed later on, a critical aspect concerns
the execution of shared tasks, whose scheduling af-
fects multiple actors. In this respect, our current pro-
posal fully addresses the management of a single cal-
endar. In contrast, it provides a partial solution to the
synchronization of multiple calendars, to be further
developed in our future work.
3.2.2 Interaction with the User
Figure 1 shows the user interface of the mixed-
initiative scheduler we developed. This user interface
is only aimed at testing the scheduling capabilities of
our prototype and we will restyle it after having col-
lected feedback from our users.
• The central portion of the page shows the user’s
schedule for the current week in a calendar and
summarizes the definition of all the allocated
tasks; see the table at the bottom of the page.
– On the right of the user’s schedule, the Schedule
start and Schedule end buttons enable the user
to request a new schedule following different
task allocation policies. If at least one schedule
solution exists:
∗ The Schedule start policy proposes one where
tasks that can be started earlier are allocated
before the others.
∗ The Schedule end policy produces a schedule
where tasks are allocated depending on their
urgency, i.e., tasks whose deadline is earlier
are allocated before the others.
The former policy produces tighter schedules,
reducing the free time slots in the user’s calen-
dar. The latter is more cautious and tends to
reserve time after the expected termination of
tasks, which might be possibly exploited for re-
covery purposes if problems occur during the
task execution.
– By clicking on a cell of the calendar the user
can view the alternative allocations of the re-
lated task in her/his schedule and can select
the one to be applied. As a consequence, the
system generates a new schedule satisfying the
user’s choice and visualizes it in the calendar (if
the user does not select anything, the schedule
is not modified).
• The lower portion of the page provides details
about the tasks allocated in the calendar. More-
over, it offers a form that enables the user to enter
tasks which do not have to be handled by the Col-
laborative Task Manager (e.g., simple “to -dos”
that are not part of a complex activity handled via
the CTM).
3.2.3 Software Components
We developed our mixed-initiative scheduler by inte-
grating two subsystems:
• The scheduling module, given a set of tasks, their
definition (e.g., duration, deadline and earliest
MIXED-INITIATIVESCHEDULINGOFTASKSINUSERCOLLABORATION
345

starting time) and the task allocation policy se-
lected by the user (schedule start or end) attempts
to allocate the tasks in the calendars of the in-
volved actors and proposes a solution, if it ex-
ists. Unless specified by the user at task definition
time, we assume that tasks cannot be scheduled in
parallel; e.g., the same person cannot attend two
meetings at the same time. Thus, the scheduler
sequentially allocates the non overlapping tasks.
• The temporal reasoner, given the current sched-
ule, the overall constraints imposed on the tasks
and a problem to be solved (e.g., adding a task to
the schedule or moving a task to a different time),
searches for safe reallocation hypotheses concern-
ing the problematic task. For this purpose, the
execution of other tasks might be shifted back or
ahead, within their starting time windows, in or-
der to reserve enough free time for the user.
4 MIXED-INITIATIVE
SCHEDULING AS A TCSP
4.1 Background
As described later on in section 4.2, the constraints
that must be satisfied by the tasks in a user’s calendar
can be represented as a Temporal Constraint Satisfac-
tion Problem (TCSP) (Dechter et al., 1991).
TCSPs are a class of Constraint Satisfaction Prob-
lems (CSPs) (Dechter, 1992) tailored to the represen-
tation of temporal constraints.
A TCSP involves a set of variables X
1
, . . . , X
n
with
continuous domains representing time points. Con-
straints can be unary or binary; a unary constraint:
(a
1
≤ X
i
≤ b
1
) ∨ . . . ∨(a
n
≤ X
i
≤ b
n
)
constrains the value of one variable X
i
to be in one of
the intervals [a
1
, b
1
], . . ., [a
n
, b
n
]. A binary constraint:
(a
1
≤ X
j
− X
i
≤ b
1
) ∨ . . . ∨ (a
n
≤ X
j
− X
i
≤ b
n
)
constrains the difference between two variables X
j
, X
i
to be in one of the intervals [a
1
, b
1
], . . ., [a
n
, b
n
].
As we shall see, TCSPs have the expressive power
to capture all of the constraints of interest to this work.
We solve TCSPs with a Constraint Logic Program-
ming (CLP) solver, as described in Section 4.3.
For implementing some important features of our
approach, we have to focus on a subclass of TCSPs,
the Simple Temporal Problems (STPs) (Dechter et al.,
1991), where all of the constraints are binary and do
not contain disjunctions:
(a ≤ X
j
− X
i
≤ b)
This class of problems can be represented as a graph
named Simple Temporal Network (STN), and it has
two important characteristics:
• checking whether a STN is consistent takes poly-
nomial time (Dechter et al., 1991; Planken et al.,
2011)
• the same polynomial algorithm used for checking
the consistency, also minimizes the STN; i.e., for
each pair of variables X
i
, X
j
, it computes an inter-
val [a
min
, b
min
] such that in every global solution,
the following holds:
a
min
≤ X
j
− X
i
≤ b
min
vice versa, for each value δ ∈ [a
min
, b
min
] there is
a global solution such that X
j
− X
i
= δ.
We solve STPs with a specialized STN solver, as de-
scribed in section 4.4.
4.2 Representing Tasks for Scheduling
Purposes
We express the time constraints in the user’s calen-
dar as TCSP constraints. Starting from the basic con-
straints defined for a task (and stored by the Collabo-
rative Task Manager), we associate two numeric vari-
ables T
s
and T
e
to the start and end time of each task
T. For simplicity, we assume that the value of a vari-
able T
s
(resp. T
e
) is the number of one-hour slots in
our calendar between Monday 8.00 and the start (re-
spectively the end) of task T.
Let us start by considering deadlines, durations
and precedences, following the example schedule
shown in Figure 1.
A deadline, such as “the Library meeting (LM)
must take place before 11.00 on Thursday”, is ex-
pressed as:
LM
e
≤ 39
since in our calendar there are 39 one-hour slots be-
tween Monday 8.00 and Thursday 11.00 (see Fig-
ure 1). With a slight abuse, we use the term deadline
also to indicate constraints on the exact end of a task;
for example, the fact that the Prog2 class (P2) must
end exactly on Wednesday at 13.00, is captured by:
P2
e
= 29
which is equivalent to 29 ≤ P2
e
≤ 29.
To express a duration, such as the fact that the Li-
brary meeting lasts 2 time slots, we simply write:
LM
e
− LM
s
= 2
A precedence, such as the fact that the Phone call
to Mr. Smith (CS) must take place after the Phd meet-
ing (PM), is expressed as:
CS
s
− PM
e
≥ 0
WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies
346

It is easy to see that all of the above constraints
can be represented not only as a TCSP, but also as a
Simple Temporal Network. However,there is an addi-
tional kind of constraints that is fundamental for com-
puting an admissible schedule of the tasks: the non-
overlapping constraints. A typical non-overlapping
constraint states that a task T cannot overlap with
another task. For example, the fact that the Library
meeting (LM) cannot overlap with the Prog2 class
(P2) is expressed as:
P2
s
− LM
e
≥ 0∨ LM
s
− P2
e
≥ 0
i.e., either LM ends before P2 starts, or vice versa.
Clearly, there must be one of these constraints be-
tween each pair of tasks T, T
′
in the calendar.
There may be additional non-overlapping con-
straints. For example, in our scenario of section 2,
the Library meeting must not take place at lunch time
(i.e. from 13.00 to 14.00) or after 17.00; to express
this constraint on Monday, we write:
LM
e
≤ 5∨ LM
e
≥ 8
LM
e
≤ 9∨ LM
e
≥ 14
similar constraints must be added for each day of the
week under consideration.
4.3 The Scheduling Module
Given the set of tasks to be allocated in the user’s cal-
endar, the scheduling module (developed by exploit-
ing the JaCoP Constraint Solver (JaCoP, 2011)) gen-
erates a schedule by handling the task definitions as
constraints to be solved in a Constraint Satisfaction
Problem. This type of activity has been largely ex-
plored in the research on Constraint Satisfaction; thus,
we briefly describe it, leaving space for the temporal
reasoning process, which is peculiar of our work.
If a task is not a precise appointment, its start and
end times are time windows during which the task has
to be executed (unless its duration is the same as the
distance between such time points). The scheduling
module thus represents the start and end time of each
task as time intervals themselves, defining them as Fi-
nite Domain Variables whose domains represent the
eligible time instants for starting/ending the task. For
instance, if a task T must start after t0, end by t1 and
its duration is d, its starting time window is [t0, t1-d].
Given the start and end Finite Domain Variables
of the tasks to be scheduled and the existing non-
overlapping constraints, the scheduling module per-
forms a domain reduction on such variables in order
to restrict their domains to the feasible values. If a
solution exists (i.e., for each Finite Domain Variable,
the domain is not null), the scheduling module ex-
plores the solution space for setting such variables to
specific values, which represent the proposed alloca-
tion time. Otherwise, the scheduling module returns a
“no solution” value, which describes the fact that the
set of considered constraints is not satisfiable, i.e., a
schedule addressing all the requirements specified by
the user cannot be generated.
Different strategies could be applied in the ex-
ploration of the solution space, leading to different
schedules. As previously described, we have selected
two alternative strategies: allocating earlier tasks be-
fore or allocating more urgent tasks before. Techni-
cally, such policies are implemented by selecting the
order of the variables to set during the exploration of
the solution space (i.e., the set of possible configura-
tions of the variables). In the Schedule start policy,
the variables having the smallest minimum values in
their domains are set before the others, which results
in an early allocation of the tasks that can start ear-
lier. In the Schedule end policy the variables having
the smallest maximum values in their domains are set
before the others, which results in an early allocation
of the tasks that must end earlier.
In order to supportan incremental mixed-initiative
scheduling of tasks, and the possibility of reason-
ing on a subset of all the tasks to be considered, the
scheduling module operates on a constraint set that
is a clone of the original task specification. In this
way, at each instant of time, the set of constraints to
be considered can be reset or modified as needed. It
is thus possible to create a history of the generated
scheduling solutions and allow the user to navigate it
and choose the preferred alternative.
It should be noticed that the constraints to be
solved in the generation of a schedule might con-
cern personal and shared tasks. Scheduling a shared
task means allocating it in the calendar of all the in-
volved actors, which are known thanks to the infor-
mation available in the Collaborative Task Manager
in which our mixed-initiative scheduler is integrated.
The scheduling module fully supports the allocation
of shared tasks because the constraints belonging to
the calendars of the involved users can be fused to
search for a global solution by merging their con-
straints: in fact, even though each actor is committed
to several tasks, those to be performed by different
actors can overlap in the overall schedule; thus, task
constraints can be merged to represent the complete
set of activities to be scheduled.
2
If the overall set of
constraints is not satisfiable (because there is no free
slot where the involved actors can perform the shared
2
If more than one actor is involved in a task to be re-
scheduled, the task instances present in the various calen-
dars are unified by imposing that their start and end times
are equal.
MIXED-INITIATIVESCHEDULINGOFTASKSINUSERCOLLABORATION
347

LMs
MPe
[2,2]
P2s
P2e
[2,2]
PMs
PMe
CSs
CSe
z
[2,2]
[1,1]
[26,39]
[25,36]
[26,36]
[29,29]
MPs
[3,3]
[27,34]
LMe
[26,35]
[27,36]
Figure 3: Basic STN for wednesday tasks.
task), the scheduling module returns a “no solution”.
However, if the failure is returned after the user has
selected one of the (conservative) suggestions made
by the temporal reasoner (see next section), it may
still be possible to request a complete (non conser-
vative) re-scheduling of all of the activities, to see if
different solutions can be found which accommodate
the new task.
4.4 The Temporal Reasoner
The deadlines, durations and precedences can be
straightforwardly expressed without disjunctions, and
therefore can be encoded in a Simple Temporal
Network (STN). Figure 3 depicts the STN for the
constraints of our running example regarding the
Wednesday tasks. It shows the new task Meet
Plumber (MP) to be inserted, as well as Library meet-
ing (LM), Prog2 class (P2), Ph.d meeting (PM) and
Phone Call to Smith (CS) (assuming that the tasks
cannot be performed before Wednesday).
The z time point represents Monday 8.00, while
the intervals on the arcs express the minimum
and maximum distance between the connected time
points; for example, interval [26, 39] on the arc con-
necting z and LM
e
represents:
26 ≤ LM
e
− z ≤ 39
i.e., LM must end at most on Thursday 11.00, and at
least on Wednesday 10.00. The dotted arc represents
the precedence between PM and CS; its associated in-
terval (omitted for readability) would be [0, +∞]; i.e.,
CS
s
must follow PM
e
by at least 0 hours.
The minimization of this STN only restricts the
intervals of the arcs z−PM
e
and z−CS
e
(the restricted
intervals are depicted in italics in the figure). In par-
ticular, the maximum value of PM
e
(end of Phd meet-
ing) becomes 35 (Wednesday 19.00) because there
must be time for making the phone call to Mr. Smith
afterwards. Similarly, the minimum value of CS
e
be-
comes 27 (Wednesday 11.00) because there must be
time for the Ph.d meeting before.
Note that this STN does not take into account
the non-overlapping constraints and, in particular, its
minimization does not affect the interval for the end
PM
e
of the new task (Meet plumber), which is still be-
tween 11.00 and 18.00 on Wednesday. Unfortunately,
not all of the time points within this interval are ad-
missible, as can be seen by considering, e.g., that the
two time slots between 11.00 and 13.00 are rigidly
allocated to the Prog2 class.
When the STN solver is invoked to show all the
feasible time intervals for starting the Meet plumber
task, we want it to return only admissible time points.
Let us start by considering how we can take into ac-
count the non-overlapping between tasks (below, we
will also discuss the non-overlapping between a task
and certain time slots, such as lunch time for the Li-
brary meeting).
From the current schedule (Figure 1), we can infer
the current order of the tasks that are already in the
calendar. We make the assumption that the order of
these tasks cannot change, while the Meet plumber
new task can be placed between any two of them.
Algorithm 1 implements this idea. It takes as in-
puts a new task T to insert, the sequence of the other
tasks (T
1
, . . . , T
k
) in the order in which they appear in
the current schedule, and an STN N encoding the ba-
sic deadline, duration and precedence constraints for
T
1
, . . ., T
k
and T. Each possible positioning of T in
the sequence determines a total order Ord among the
tasks (including T); such a total order is asserted as a
set of precedence constraints into N , and the result-
ing net is minimized, yielding an interval [min
i
, max
i
]
of possible values for the start T
s
of T.
The algorithm returns a set FInt containing all of
such intervals. If the current order of the tasks is not
allowed to change, the intervals in FInt represent all
Algorithm 1: Feasible intervals for adding a new task.
input:
new task T
other tasks in current schedule order (T
1
, . . . , T
k
)
STN N (deadlines, durations, precedences)
FInt ⇐
/
0
for i = 0. . . k do
Ord ⇐ (T
1
, . . . , T
i
, T, T
i+1
, . . . T
k
)
N
′
⇐ assert order Ord in N
N
′
⇐ minimize N
′
FInt ⇐ FInt ∪
{ get interval [min
i
, max
i
] for T
s
from N
′
}
end for
return FInt
WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies
348

LMs
MPe
[2,2]
P2s
P2e
[2,2]
PMs
PMe
CSs
CSe
z
[2,2]
[1,1]
[26,39]
[25,36]
[26,36]
[29,29]
MPs
[3,3]
[27,34]
LMe
[32,33]
[34,35]
[26,27]
[35,36]
[29,30]
Figure 4: STN for order (LM, P2, MP, PM, CS).
of the possible choices for starting task T.
Going back to our example scenario, the new task
is MP, the other tasks (in the current scheduled order)
are (LM, P2, PM, CS), and the basic STN N is the
one depicted in Figure 3. Figure 4 shows the net N
′
computed by the algorithm at the 3rd iteration (i = 2),
when the new task MP is placed between P2 and PM.
First of all, several intervals are restricted due to
the minimization. In particular, the interval on the
arc z−MP
e
is restricted to [32, 33] (Wednesday from
16.00 to 17.00); when we ask the STN for the inter-
val on the arc z−MP
s
, we get [29, 30] meaning that,
if MP is placed between P2 and PM, it can start on
Wednesday between 13.00 and 14.00.
The full execution of the algorithm yields the fol-
lowing set of intervals:
/
0 when MP is the first task
/
0 when MP is between LM and P2
[29, 30] when MP is between P2 and PM
[31, 31] when MP is between PM and CS
/
0 when MP is the last task
If we take the union of the overlapping intervals, we
conclude that the meeting with the plumber can start
on Wednesday from 13.00 to 15.00 (interval [29,31]).
Let us now show how it is possible to handle the
non-overlappingbetween a task and certain time slots,
by assuming that the user is not satisfied with the in-
terval [29,31] for PM
s
computed by Algorithm 1, be-
cause it would be preferable to meet the plumber in
the morning. The user then attempts to make room for
MP by selecting the Library meeting task and asking
the STN solver to suggest where to move this task.
The computation of the possible start intervals of
LM is made with an algorithm similar to Algorithm 1,
which explores the effects of placing LM in each
position within the current order of the other tasks
(P2, PM, CS). However, there is a parallel ordering
to be explored; if we denote respectively as I1, I2
LMs
[2,2]
P2s
P2e
[2,2]
PMs
PMe
CSs
CSe
[2,2]
[1,1]
LMe
I1s
[1,1]
I1e I2s
[3,3]
I2e
Figure 5: Moving LM after P2 in the afternoon.
the lunch time (13.00 to 14.00) and the late afternoon
(17.00 to 20.00) on Wednesday, the algorithm must
also explore the placement of LM in each position
within the order (I1, I2). Figure 5 shows a portion
of the STN where LM has been placed between P2
and PM in the order of tasks, and between I1 and I2
in the order of non-admissible slots.
The minimization of this particular network yields
an interval [30,31] for starting LM (14.00 to 15.00).
The algorithm also explores all the other combina-
tions of the position of LM in the tasks order and in
the non-admissible slots order, yielding the following
admissible starting intervals:
[24, 25] LM first task before lunch
[30, 31] LM between P2 and PM after lunch
[31, 31] LM between PM and CS after lunch
[36, 37] LM on Thursday after Write paper
If we take the union of the overlapping intervals, we
conclude that we can start LM on Wednesday from
8.00 to 9.00 or from 14.00 to 15.00, and on Thursday
from 8.00 to 9.00. Going back to the goal of the user,
the Library meeting can be moved to Wednesday af-
ternoon or Thursday morning, saving room for task
Meet plumber on Wednesday morning.
It should be noticed that the described techniques
could be extended to handle shared tasks. For exam-
ple, after computing the slots where the Library meet-
ing could be placed, we have only taken into account
the current user’s calendar. However, it might be nec-
essary or desirable to also take into account the calen-
dars of the other people attending the meeting.
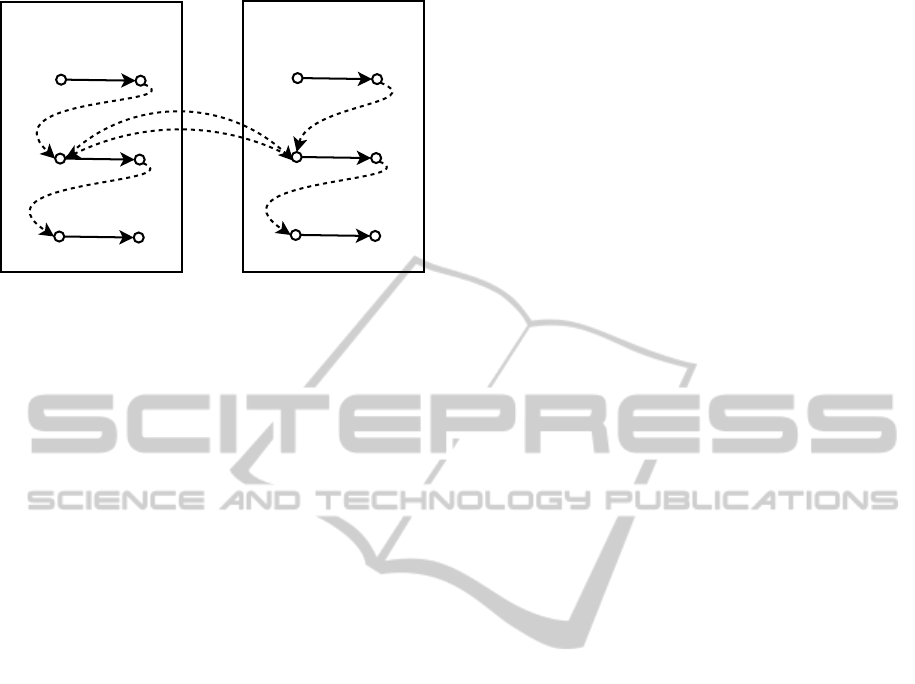
It is out of the scope of this paper to present the
extended techniques that address this issue. In Fig-
ure 6 we give a hint of how a (portion of) STN en-
compassing multiple calendars may look like. There,
tasks B and V of USR1 and USR2 represent the same,
shared task (e.g., a meeting), and this is expressed in
the net by the fact that B
s
− V
s
≥ 0 and V
s
− B
s
≥ 0,
i.e. B
s
= V
s
. The extensions needed to handle such an
MIXED-INITIATIVESCHEDULINGOFTASKSINUSERCOLLABORATION
349

As
Bs
Be
Ae
USR1
Cs
Ce
Us
Vs
Ve
Ue
USR2
Ws
We
Figure 6: A multi-user scenario with cross-dependencies.
STN may benefit from distributed solving of the Sim-
ple Temporal Problem (Boerkoel and Durfee, 2010)
and may involve negotiations among the schedules
of different users (as partially done in (Tarumi et al.,
1997), where a user affected by a change made by an-
other user can accept or refuse it).
5 RELATED WORK
The support offered by our mixed-initiative sched-
uler can be compared to various types of systems, de-
scribed in the following.
Meeting support services help the user identify-
ing suitable time slots for allocating shared tasks on
the basis of the availability of the actors to be in-
volved. See, for instance Google Calendar (Google,
2012) and previous agent-based meeting scheduling
services such as the one described in (Macho et al.,
2000). However, such tools do not provide any
scheduling support.
To-do-list managers, such as Remember The Milk
(Remember The Milk, 2011), are connected to the
user’s calendar but typically do not provide any
scheduling support. They only present the lists of
things allocated in a certain time slot.
Task managers, such as Things (Cultured Code,
2011) and DoIt (DoIt.im, 2011), support the manage-
ment of tasks, deadlines and task dependencies but
they do not schedule tasks, either.
Opportunistic schedulers, typically based on plan-
ning technology, synchronously guide the user in the
execution of activities according to the pending goals
to be achieved. However, they do not provide the user
with an overviewof long-term schedules, do not man-
age the shared activities and are not mixed-initiative:
they basically suggest opportunities of action, which
the user may accept or ignore. For instance, see
(Horvitz and Subramani, 2007).
Complex schedulers plan the execution of tasks ac-
cording to deadlines and to the surrounding context,
e.g., in mission planning and robotic applications.
However, they are developed for very particular envi-
ronments and are not suitable for managing the user’s
daily schedules, which is a goal of our work, nor for
handling parallel activity contexts. In contrast, this
is possible in our work because our mixed-initiative
scheduler is integrated with a generic Collaborative
Task Manager handling parallel activity contexts.
Temporal reasoning and scheduling have been in-
troduced in some process management tools to ad-
dress their lack of capability to reason about time.
In (Senkul and Toroslu, 2005) the authors make
use of the Oz multi-paradigm programming language
(Wurtz, 1996) for solving scheduling problems with
CLP techniques similar to the ones at the base of the
JaCoP Constraint Solver used in our work. In (Mans
et al., 2010), a dedicated Java service is used for sim-
ilar purposes. Some process management tools, such
as the one described in (Eder et al., 2003), perform
temporal reasoning to estimate the date where a cer-
tain task will have to be done, with the aim of en-
abling the user to foresee her/his future schedules.
This kind of feature is complementaryto those offered
by our system. Other tools, such as WorkWeb System
(Tarumi et al., 1997), schedule multiple workflows by
taking the availability of actors and resources (e.g.,
meeting rooms) into account. The main role of the ac-
tors’ personal schedulers (named Pochet) is that of au-
tomatically (or manually) accepting or rejecting new
tasks and modifications proposed by other agents.
To the best of our knowledge, none of the men-
tioned works supports the kind of mixed-initiative
process which is at the core of our method, i.e., the
ability of the user to invoke the temporal reasoner
module as a support tool for reasoning about the pos-
sible places where specific tasks can be (re)allocated
and thus to pro-actively guide the schedule revision.
6 CONCLUSIONS
We described a mixed-initiative scheduler which sup-
ports the organization of the user’s activities in a
calendar by proposing safe schedules (respecting the
user’s commitments) and by suggesting conservative
schedule revisions when new tasks occur. Our system
also helps the user to identify alternative allocations
of tasks, which guarantee that the overall schedule is
satisfiable. At the current stage, our mixed-initiative
scheduler fully supports the management of personal
tasks. However, it partially supports the scheduling
of shared tasks: it generates global schedules if at
WEBIST2012-8thInternationalConferenceonWebInformationSystemsandTechnologies
350

least one solution satisfying the overall set of con-
straints exists, but it does not support the search for
solutions for repairing to scheduling failures. In our
future work we will extend the system to deal with
such situations by improving the temporal reasoner
that supports the task re-allocation and by developing
an interaction protocol that helps the involved users to
reach an agreement on schedule modifications. Our
future work will also be devoted to testing the scal-
ability of our scheduler and its usability, checking it
with end-users to improve its user interface and inter-
action features.
REFERENCES
Allen, D. (2003). Getting Things Done: the art of stress-
free productivity. Penguin.
Ardissono, L. and Bosio, G. (2012). Context-dependent
awareness support in open collaboration environ-
ments. User modeling and user-adapted interaction
- The Journal of Personalization Research, to appear.
Ardissono, L., Bosio, G., Goy, A., Petrone, G., and Seg-
nan, M. (2012). Integration of cloud services for web
collaboration: A user-centered perspective. In Models
for Capitalizing on Web Engineering Advancements:
Trends and Discoveries, pp. 1–19. IGI Global.
Ardissono, L., Bosio, G., Goy, A., Petrone, G., Segnan,
M., and Torretta, F. (2011). Collaboration support
for activity management in a personal cloud. Interna-
tional Journal of Distributed Systems and Technolo-
gies, 2(4):30–43.
Boerkoel, J. and Durfee, E. (2010). A comparison of al-
gorithms for solving the multiagent simple temporal
problem. In Proc. of 20th Int. Conf. on Automated
Planning and Scheduling.
Cultured Code (2011). Things Mac.
http://culturedcode.com/things/.
Dechter, R. (1992). Constraint networks (survey). In Wiley,
J. and Sons, editors, Encyclopedia of Artificial Intelli-
gence (2nd ed.).
Dechter, R., Meiri, I., and Pearl, J. (1991). Temporal con-
straint networks. Artificial Intelligence, 49:61–95.
DoIt.im (2011). Doit anywhere, any time!
http://www.doit.im/.
Eder, J., Ninaus, M., and Pitchler, H. (2003). Personal
schedules for workflow systems. In Proc. of Int. Conf.
on Business Process Management, LNCS 2678, pp.
216–231, Eindhoven, NL.
Google (2012). Google calendar. calendar.google.com.
Horvitz, E. and Subramani, M. (2007). Mobile opportunis-
tic planning: methods and models. In LNAI n. 4511:
Proc. 11th Int. Conf. on User Modeling, pp. 228–237,
Corfu, Greece.
JaCoP (2011). JaCoP - Java Constraint Programming
solver. http://www.jacop.eu/.
Macho, S., Torrens, M., and Faltings, B. (2000). A multi-
agent recommender system for planning meetings. In
Proc. of the Agents’2000 workshop on Agent-based
recommender systems (WARS’2000), Barcelona.
Mans, R., Russell, N., van der Aalst, W., Moleman, A., and
Bakker, P. (2010). Schedule-aware workflow manage-
ment systems. Springer.
Planken, L., de Weerdt, M., and van der Krogt, R. (2011).
Computing all-pairs shortest paths by leveraging low
treewidth. In In Proc. of 21st Int. Conf. on Automated
Planning and Scheduling.
Remember The Milk (2011). The best way to manage your
tasks. never forget the milk (or anything else) again.
http://www.rememberthemilk.com/.
Senkul, P. and Toroslu, I. (2005). An architecture for work-
flow scheduling under resource allocation constraints.
Information Systems, 30:399–422.
Tarumi, H., Kida, K., Ishiguro, Y., Yoshifu, K., and
Asakura, T. (1997). WorkWeb system - multi-
workflow management with a multi-agent system. In
Proc. of Int. ACM SIGGROUP Conference on Sup-
porting Group Work, pp. 299–308, New York, NY.
Van der Aalst, W., Ter Hofstede, A., Kiepuszewski, B., and
Barros, A. (2008). Conformance checking of service
behavior. ACM Trans. on Internet Technology (TOIT),
Spec. Issue on Service-oriented Computing, 8(3):art.
13.
Wurtz, J. (1996). Constraint-based scheduling in oz. In Se-
lected Papers of the Symp. on Operational Research.,
pp. 218–223.
MIXED-INITIATIVESCHEDULINGOFTASKSINUSERCOLLABORATION
351