
AN OPEN-LOOP ENERGY NEUTRAL POWER MANAGER
FOR SOLAR HARVESTING WSN
Andrea Castagnetti, Alain Pegatoquet, C´ecile Belleudy and Michel Auguin
University Nice Sophia Antipolis, LEAT-CNRS, 250 Rue Albert Einstein, 06560 Valbonne, France
Keywords:
Wireless Sensor Networks, Solar Energy Harvesting, Power Management.
Abstract:
Energy harvesting Wireless Sensor Networks are receiving increasing interest due to their potential to extend
system lifetime. Because environmental energy availability is highly variable, an efficient power management
is required. An energy harvesting power manager must adapt to different situations that depends on the energy
that can be harvested from the environment. In this paper we propose a generic model for solar energy
harvesting wireless sensor node, that we validate on real hardware. A novel power management architecture is
then proposed. Simulation results show that up to 30% performance improvement can be achieved compared
to a state of the art power management algorithm.
1 INTRODUCTION
Wireless Sensor Networks (WSNs) consists of dis-
tributed autonomous sensors that can operate with-
out a pre-established infrastructure. WSNs are used
for monitoring environment (temperature, humidity,
etc.), fire surveillance, high precision agriculture and
many other applications. Due to their physically em-
bedded nature, WSNs are well suited for energy-
harvesting. This offers an alternative solution to the
problem of the energy limitation that arise from the
fact that sensor nodes are equipped with small bat-
teries. More often, due to the fact that nodes are de-
ployed in harsh environment, batteries cannot be re-
placed. Virtually, the lifetime of an energy-harvesting
WSN node is only limited by the hardware reliabil-
ity. However we argue that the potential of an energy-
harvesting WSNs node cannot be exploited without
an efficient power management system.
In battery-powered system, the goal of a power
manager is to minimize the power consumption in
order to maximize the lifetime of the battery. At
the opposite energy-harvesting systems can experi-
ence peak of energyavailability. During those periods
the system can provide peak quality of service (QoS)
only using the energy coming from the environment.
Those periods are interleaved with intervals in which
the environment provides only small amount of en-
ergy, or even nothing. When an energy-harvesting
node operates on battery, performance must be ad-
justed to extend the lifetime of the node until suffici-
ent energy will again be provided by the environment.
From the situations sketched above it becomes
clear that different power management techniques can
be used depending on environmental conditions. As
an example, consider the case in which a sufficient
amount of energy can be harvested from the environ-
ment. The power manager can then decide to operate
the system in energy neutrality, that is balancing the
energy consumed (to perform the task) and the har-
vested energy.
In this paper we address the problem of power
management for energy-harvesting WSNs starting
from a modeling perspective. We propose a generic
model that permits to describe a solar energy-
harvesting node in a compact form. The derived
model is validated on a recent solar energy harvest-
ing sensor platform. Based on this framework, we
propose a novel architecture, called Open-Loop en-
ergy neutral Power Manager (OL-PM). This power
manager is validated in simulation. We have also
adapted the power manager presented in (Kansal
et al., 2007) to our model and we compared its per-
formance against our power manager. Experimen-
tal results are very encouraging as up to 30% data
throughput improvement can be achieved. Moreover
we have observed that the battery is never completely
discharged using our power manager, that leads to an
improvement on system reliability. Finally the im-
pact of the power management reactiveness on the
system’s performance has been studied.
352
Castagnetti A., Pegatoquet A., Belleudy C. and Auguin M..
AN OPEN-LOOP ENERGY NEUTRAL POWER MANAGER FOR SOLAR HARVESTING WSN.
DOI: 10.5220/0003942703520358
In Proceedings of the 2nd International Conference on Pervasive Embedded Computing and Communication Systems (PECCS-2012), pages 352-358
ISBN: 978-989-8565-00-6
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK
In recent years several energy harvesting technology
have emerged. Besides solar panels (Nelson, 2003)
and wind generators, vibration scavengers, thermal-
to-electricity (Toriyama et al., 2001) and electromag-
netic converters (Yi et al., 2007) have also been pro-
posed. Many energy harvesting systems also need en-
ergy storage because they have to continue operation
even when no energy is available from the environ-
ment (i.e. during night for a solar harvesting system).
Nowadays rechargeable batteries are used for long-
term energy storage. However new technologies are
emerging like supercapacitors (Shin et al., 2011).
Besides the problem of designing an energy har-
vesting system that effectively extract and store en-
ergy the issue of an efficient power management pol-
icy must be faced. Research on energy harvesting
power management has gained lot of attention in re-
cent years mainly in the field of wireless sensor net-
works. One of the earliest work on energy harvest-
ing power management has been presented in (Kansal
et al., 2004). Duty-cycling is used to adjust the power
consumption of a WSN node. During an initializa-
tion phase the characteristics of the energy source are
learned. Then a fixed duty-cycleis applied. The effec-
tiveness of this solution depends on the variability of
the energy source. A more principled algorithm for
dynamically adapting the the duty-cycle of a sensor
node is discussed in (Kansal et al., 2007). The authors
assume that the energy source is periodic. A period is
then divided into intervals of equal duration. An es-
timate of the energy input, that is assumed to be con-
stant over the course of a single block, is computed
from historical data. Duty-cycle is then set for each
block based on an initial estimate. Online changes
are applied if there is a mismatch between the actual
energy received and the expected energy computed
by the model. The reactiveness of this power man-
agement solutions, that is the ability to adapt to en-
vironmental variations, mainly depends on the initial
choice of intervals duration. In the work of (Kansal
et al., 2007) this duration was fixed to 30 minutes.
The authors also present the notion of energy neutral
operation, that is the ability to operate such that the
energy used is always less than the energy harvested.
They use this concept to develop the energy neutral
power manager discussed above.
The work of (Kansal et al., 2007) is extended in
(Vigorito et al., 2007). Here the authors use tech-
niques from adaptive control theory to increase the
adaptivity of an energy harvesting power manager.
This power manager only uses the current battery
level of the node to make duty-cycling decisions. This
approach is then model-free with respect to the energy
source. The powermanager is validated in simulation.
Experimental results show that an average 16% per-
formance improvement can be achieved compared to
the power manager proposed by (Kansal et al., 2007).
3 SYSTEM MODEL
In this Section we present the system model that is
composed of three main components: the platform
load, the energy harvesting and the battery.
3.1 A Task Level Platform Load Model
The Figure 1 represents a formalization of the plat-
form load. As shown, the platform load is first char-
Figure 1: Formalization of the platform load.
acterized by a wake-up period T
wi
. During this period,
the platform is first active, then inactive. An active pe-
riod may be composed by several activities that cor-
respond to different current consumption. A typical
active period is composed of Sensor, CPU and RF ac-
tivities. However, in order to get a platform model
as much general as possible, different activities hav-
ing their own period that can be different from the
wake-up period can be defined. For example, in Fig.
1 two different kinds of activities have been defined:
sensing and transmission. The sensing activity is ex-
ecuted every wake-up period (T
wi
), while the trans-
mission occurs with a period T
Tx
. During the inactive
period the system enters sleep state for power saving.
Q
sense
is the charge delivered by the battery when the
sensing task is executed, which accounts for the cur-
rent consumed by the microcontroller and the sensor.
When the transmission task is also executed, there is
an increase in the current consumption and the battery
delivers supplementary Q
TX
Ampere-hour of charge
compared to previous case. The rate at which the bat-
tery is discharged depends on the average discharge
current. This parameter can be computed using our
model and it is represented by the α factor that is de-
fined as follows:
α =
Q
T
wi
(1)
AN OPEN-LOOP ENERGY NEUTRAL POWER MANAGER FOR SOLAR HARVESTING WSN
353
α denotes the charge consumed by the platform over
a wake-up period. In other words α is the average
current delivered by the battery during a wake-up pe-
riod. This parameter can be computed independently
for each activity (e.g. sensing, RF transmission) en-
abling a modular and accurate characterization of the
application.
3.2 A Battery and Energy Harvesting
Integrated Model
We model the solar panel and the recharge circuit us-
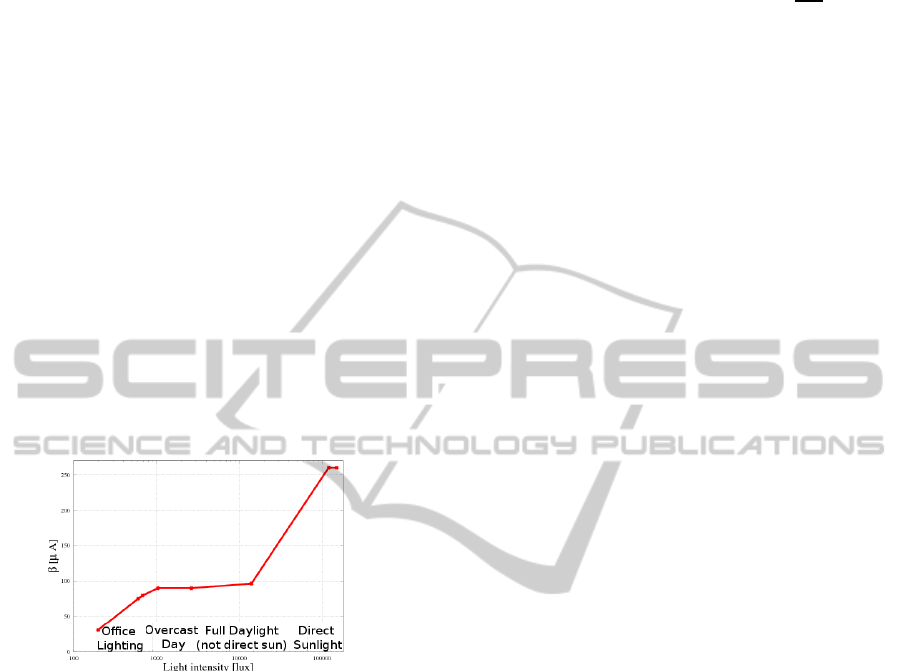
ing a parameter, called β, which is a function of the
light intensity. The β parameter models both the ef-
ficiency of the solar panel and the efficiency of the
voltage regulator and the charge circuit that are used
to recharge the battery. This parameter is expressed in
Ampere and indicates the rate at which the solar panel
can recharge the battery under a fixed light intensity.
Figure 2 shows the β parameter as a function of the
Figure 2: β for different light conditions.
light intensity expressed in Lux using a logarithmic
scale. The curve was extracted through experimen-
tations for a 2.25in x 2.25in solar panel and a 100
µAh Li-Ion battery. More parameters can be taken
into account in order to refine the model, e.g. the type
of light (fluorescent, incandescent, sun light) and its
spectral characteristics, the quantum efficiency of the
solar cell and more. Although simple, our model pro-
vides a good approximation of the energy that can be
harvested by the system and help defining the appli-
cation load requirements and the power management
policies.
3.3 A Battery State of Charge Model for
Periodic Workload
Using the α and β parameters introduced in Sections
3.1 and 3.2, the state of charge (SoC) of a battery for
the next n wake-up periods (Twi) can be computed
using equation 2:
SoC(t + nT
wi
) = SoC(t) + [β− (α
s
+ α
Tx
T
wi
T
Tx
)]nT
wi
− K
leak
nT
wi
(2)
Where α
s
and α
Tx
are the current consumption for
sensing and transmission respectively. The Eq. 2 is
true if the conditions 3, 4 and 5 are respected.
SoC(t = 0) = SoC
max
(3)
SoC
min
≤ SoC(t + nT
wi
) ≤ SoC
max
(4)
β, α
s
and α
Tx
are constants on [t, t + nT
wi
] (5)
SoC
max
represents the capacity of the battery. We con-
sider that the battery is fully charged at t = 0 (3).
As the battery can neither store more charge than
its capacity nor be discharged too deeply, its SoC is
bounded between SoC
max
and SoC
min
(4). Finally and
for sake of simplicity, Eq. 2 is true if the luminosity
(β) and the average discharge current over a wake-
up period (α) are constants (5). If these parameters
are changing during this period, Eq. 2 can be eas-
ily divided into smaller period intervals. The leakage
current is modeled with the K
leak
parameter. This pa-
rameter models two effects: the battery self discharge
and the current drawn by the platform during inactive
periods (e.g. the low-power mode current consump-
tion).
3.4 Model Validation using the EZ430
Platform
We conducted a set of tests to validate our SoC esti-
mation approach. The Texas Instruments EZ430 solar
energy harvesting platform (TexasInstruments, 2011)
was used as experimental platform. This platform
is equipped with a 2.25in x 2.25in solar panel opti-
mized for operating indoor under low-intensity fluo-
rescent light. The energy harvested by the solar panel
is stored in a 100 µAh Li-Ion rechargeable battery.
The application board is equipped with an MSP430
microcontroller and a CC2500 RF transceiver. The
board is programmed with an End Device (ED) ap-
plication that periodically sends a packet over the air
to a base station. During the idle period both the mi-
crocontroller and the radio chip are put into a sleep
state.
We used Equation 2 to predict the SoC, then the
lifetime (LT) of the system under different light con-
ditions. The estimated and measured life-times (LT)
are compared for different wake-up periods. The re-
sults are shown in Tab. 1. As it can be observed, the
model is accurate as the error always remains below
PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems
354
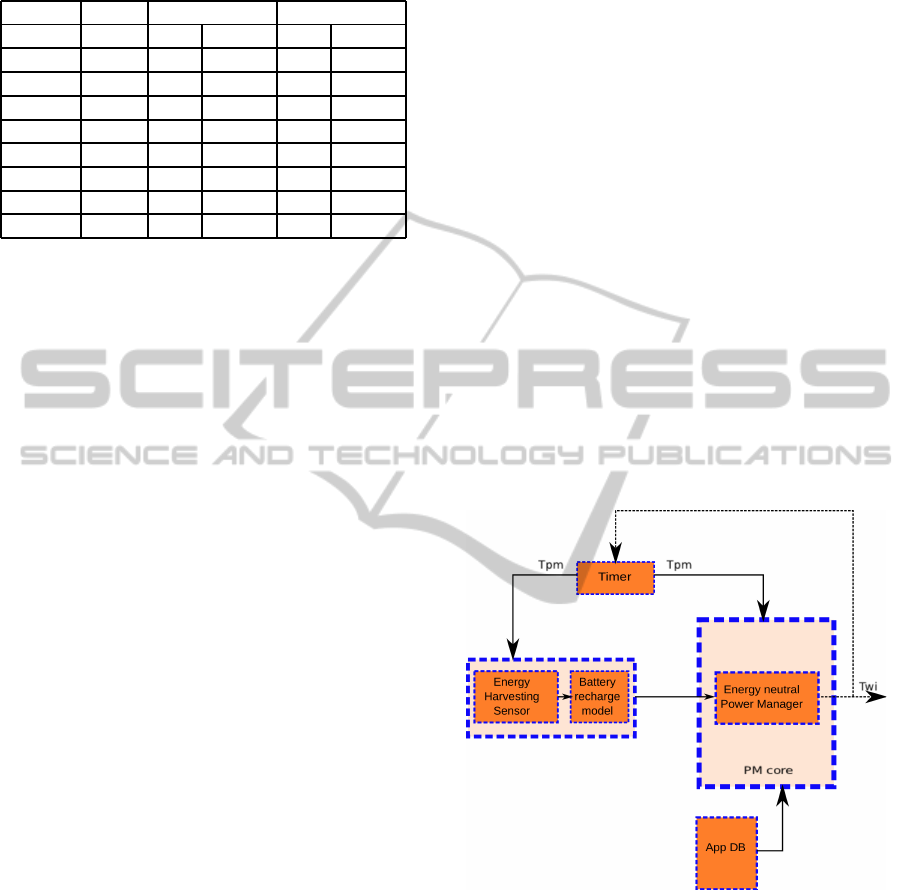
Table 1: Validation of the SoC estimation technique (LT in
minutes).
0 lux ≃ 200 lux
T
wi
[sec] α [µA] LT LT LT LT
(exp) (model) (exp) (model)
1 128.52 28 29 50 38
2 64.26 54 59 140 112
3 42.84 83 88 312 332
4 32.13 107 117 / +∞
6 21.42 162 176 / +∞
10 12.85 290 294 / +∞
20 6.43 585 587 / +∞
10% for 0 lux. It is interesting to note that with a
T
wi
of 20 seconds the tests lasts for 10 hours while
the lifetime prediction error is only 2 minutes. The
prediction error slightly increases for 200 lux, but the
model still gives accurate results. Actually, during ex-
perimentations the luminosity fluctuates around 200
lux. This is why we observe a higher deviation of the
model than without energy harvesting (β = 0). For
a T
wi
higher or equal to 4 seconds the energy har-
vested (β) is higher than the energy consumed (α),
so the system is working in energy neutral conditions.
Therefore the LT is theorically infinite (∞). Despite
our model has been validated on the TI EZ430 plat-
form, it is applicable to a wide range of platforms.
3.5 Range of Applicability of the Model
In this section we discuss how our model can adapt
to different architectures. We first analyze the plat-
form load model proposed in Section 3.1. The power
consumption usually changes according to the voltage
supply. Nowadays electronics can be powered with a
wide voltage range. If a switching regulator (e.g. a
buck regulator) is used to provide regulated power to
the load then the current that it draws from the battery
will change according to its input and output voltage.
In this case the α parameter must be rescaled by a fac-
tor that takes into account the efficiency of the switch-
ing regulator. At the opposite, if a linear regulator is
used, as in our case, it is reasonable to consider α to
be independent from the battery voltage.
In Section 3.2 we proposed to model the recharge
process with a β parameter, which is a function of the
light intensity. The solar cell and recharge circuit are
then modeled as a simple current generator. Some as-
sumptions must be made in order for this model to be
valid. First of all the operating point of the solar panel
must be forced by a proper circuit (i.e. MPPT control
circuit). Moreover the efficiency of the recharge cir-
cuit will vary a lot depending on the output voltage of
the solar cell. Finally, the capacity of the battery will
have a huge impact on the recharge process. In our
model all the variables which have an impact on the
efficiency of the recharge process are implicitly in-
cluded in the β parameter. Of course β will change for
a different solar panel and so the model would have to
be re-calibrated.
4 OPEN-LOOP ENERGY
NEUTRAL POWER MANAGER
In this Section we consider the problem of adapting
the performance and the power consumption of the
system to the available energy. Performance scaling
is achieved by varying the wake-up period (T
wi
) of
the sensor node. Duty-cycling between active and
low power states is very effective in reducing the
power consumption. Moreover, almost all the WSNs
nodes features one or more low-power states. Figure
3 shows the architecture of an Open-loop power man-
ager (OL-PM). We use the name open-loop to under-
Energy neutral
Power Manager
Energy
Harvesting
Sensor
Battery
recharge
model
Timer
Figure 3: Open-loop power manager architecture.
line the fact that the decision of the power manager is
based only on the current value of β. The power man-
ager does not use the SoC prediction to compute the
current value of T
wi
. The system is composed of four
main blocks:
Power Manager Timer (T
pm
). The power man-
ager is executed periodically, with a period that is a
multiple of the wake-up period T
wi
. Every time T
wi
changes, this timer is set to n times T
wi
. Limiting the
execution of the power manager reduces the overhead
but it also limits the reactiveness. The trade-off be-
AN OPEN-LOOP ENERGY NEUTRAL POWER MANAGER FOR SOLAR HARVESTING WSN
355
tween overhead and reactivity can be tuned by adjust-
ing the n parameter.
Energy Harvesting Sensor and Battery
Recharge Model. An energy harvesting sensor is
used to estimate the recharging rate of the battery.
This value will then be used to compute the recharge
rate using the battery recharge model, namely β. For
a solar panel the harvesting sensor could be a current
meter that measures the output current of the solar
panel. If it is not possible to measure the output
current of the solar cell, the energy harvesting sensor
can be replaced by a light meter.
System Parameters Database (AppDB). The T
wi
settings as well as the task level platform loads (α
i
)
are stored in a database.
Energy Neutral Power Manager. This block im-
plements the power management strategy. By balanc-
ing the α and β parameters, the system works with
only the energy coming from the environment. In this
case the SoC of the battery is constant over the time.
Its value depends on the past history, i.e. how much
time the system has worked in both negative and pos-
itive energy conditions. Using Equation 2 the condi-
tion for energy neutrality can be expressed as follows:
SoC(t) = SoC(t + nT
wi
) (6)
This condition leads to the following energy neutral
wake-up period:
T
wi
=
l
Q
β− K
leak
m
(7)
As T
wi
is an integer the result of Eq. 7 must be approx-
imated (the decimal part must be removed). The ceil
function is used to round toward the nearest energy
neutral.
5 SIMULATION RESULTS
We compared the OL-PM with the power manager
presented in (Kansal et al., 2007) that we have
adapted to the model discussed in Section 3. We sim-
ulated the two power managers on a five days solar
energy data set. This Section presents the simulation
setup as well as the simulation results.
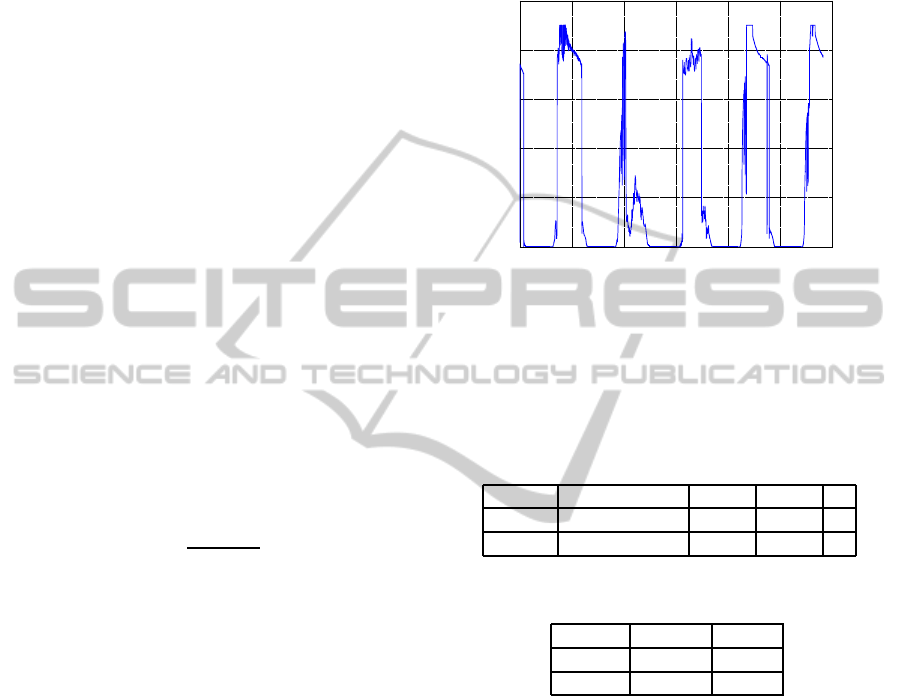
5.1 Simulation Setup and Energy Data
Set Profile
The values for the α parameter were measured for the
TI EZ430 platform (some are reported in Tab. 1). In
order to get realistic values for the β parameter we
measured the light intensity in an office. We con-
nected a luxmeter to a PC and repeatedly measured
the light intensity at an interval of five seconds during
five days. The values for the β parameter were then
computed using the function of Fig. 2. The results are
plotted in Fig. 4. The system parameters are shown in
0
20
40
60
80
100
0 20 40 60 80 100 120
β [µ A]
Time [hours]
Figure 4: The values of β during five days in an office.
Table 2. The overhead of a power management exe-
cution (Q
pm
) has been considered equal to the charge
consumed for a RF transmission.
The battery parameters are reported in Tab. 3.
Table 2: System parameters.
T
wi
[min, max] Q
tx
Q
pm
n
[sec] [µAs] [µAs]
OL-PM [1, 120] 128.52 128.52 10
Table 3: Battery parameters.
SoC
min
SoC
max
C
d
[µAh] [µAh] [µAh]
37 100 63
5.2 Evaluation Metrics
In order to evaluate both power managers we have de-
fined different metrics:
• Average Data-rate (hRdi). It is a metric of the
performance of the power manager. It is defined
as the ratio between the size of the packet that is
sent (we use a payload of 33 bytes) and the wake-
up period, T
wi
. The average is computed over the
five days, including the periods of time where the
battery is fully discharged (in this case the data-
rate is zero).
• Maximum and Minimum Data-rate (Rdmax,
Rdmin). Those metrics give an indication of the
peak and minimal performance achievable by a
node using a given power manager.
PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems
356
• Average SoC (hSoCi). To assess if the power
management algorithm drift. Actually, the aver-
age SoC can be used to determine how far the de-
cisions of the power manager are from the energy
neutral condition.
• Battery Failures (B
f
). This metric gives a mea-
sure of the correctness and reliability of the power
manager’s choices. A value of 0 means that the
battery is never fully discharged and the node is
always operational.
5.3 Experimental Results
Simulation results for the power manager are reported
in Tab. 4.
Table 4: Performance comparison of Kansal algorithms
(Kansal et al., 2007) and the OL-PM.
hRdi Rd
max
Rd
min
hSoCi B
f
[bits/s] [bits/s] [bits/s] [µAh]
Kansal 29.55 132 0 65.81 9
OL-PM 44.61 132 2.2 88.8 0
From Tab. 4 it can be observed that for the data set
used the OL-PM improves the data-rate by more than
30% compared to the algorithm proposed by (Kansal
et al., 2007). This can be mainly explained by the
fact that the data set has a high energy variability
as it can be observed from Fig. 4. The OL-PM is
able to exploit this variability thanks to of its reactiv-
ity (that can be tuned through the n parameter). The
activation period of this power manager is in the or-
der of tens of seconds. The algorithm proposed by
(Kansal et al., 2007) takes a different approach. It
samples the energy source each 30 minutes and it also
uses an EWMA filter to predict the energy availabil-
ity. The combination of those two effects excessively
smoothes the data from the energy harvester (β), and
the power manager cannot exploit the peak of energy
availability to increase the data-rate (Rd). The dif-
ferences in reactivity also explains that the battery is
never fully discharged for the OL-PM, while it hap-
pens nine times in five days for Kansal. As a con-
sequence the node stops sending data, for a variable
amount of time, on average two times a day.
Rd
max
is the same for the two algorithms, as it de-
pends on the peak energy harvested by the solar panel,
which is the same in both cases. It is interesting to
note that both power managers’ goal is to operate the
system in energy neutrality. In perfect conditions the
average SoC of the battery should be equal to the ini-
tial SoC (in our case SoC
max
). Inaccuracies in β esti-
mation and lack of reactivity cause a SoC drift. The
drift is only 10µAh, that is 16% of the discharge ca-
pacity (C
d
) for the OL-PM. It can accurately track the
variation of β and it can operate the system near the
energy neutrality. At the opposite the Kansal algo-
rithm produces a drift of 34µAh, that is 54% of the
discharge capacity C
d
. This is due to the assumption
made by the authors that the energy harvested is con-
stant over a period of 30 minutes. Actually this as-
sumption is violated many times in our data set. We
therefore conclude that considering the harvested en-
ergy constant over a long period (i.e. 30 minutes)
could lead to performance degradation.
The rest of our experiments investigated the im-
pact of varying the reactivity of the power manager,
on the overall performance of the OL-PM. Figure 5
shows the average SoC, the average data rate and the
SoC
min
obtained for different values of n. As previ-
30
40
50
60
70
80
90
100
5 10 15 20 25 30
<SoC> [µAh], <Rd> [bits/s], SoC
min
[µAh]
n
<SoC>
SoCmin
<Rd>
<SoC>
SoCmin
<Rd>
Figure 5: The effects of varying the power manager reactiv-
ity (n) on the hSoCi, SoC
min
and hRdi.
ously discussed the more the SoC diverges from the
SoC
max
the more the energy neutrality condition is vi-
olated. Experimental results show that for a n smaller
than 10 the system tends to perform poorly. Actually
the gain induced by the increased reactivity is coun-
terbalanced by the overhead. The impact of the power
management overhead is higher when β is lower (i.e.
during night). During those periods the system can-
not actually work in energy neutrality even with the
smallest value of T
wi
. As it can be seen, the aver-
age SoC as well as the average data-rate tends to be-
come stable for a n comprised between 10 and 20. For
values greater than 20 the lack of reactiveness of the
power manager deteriorates the global performance.
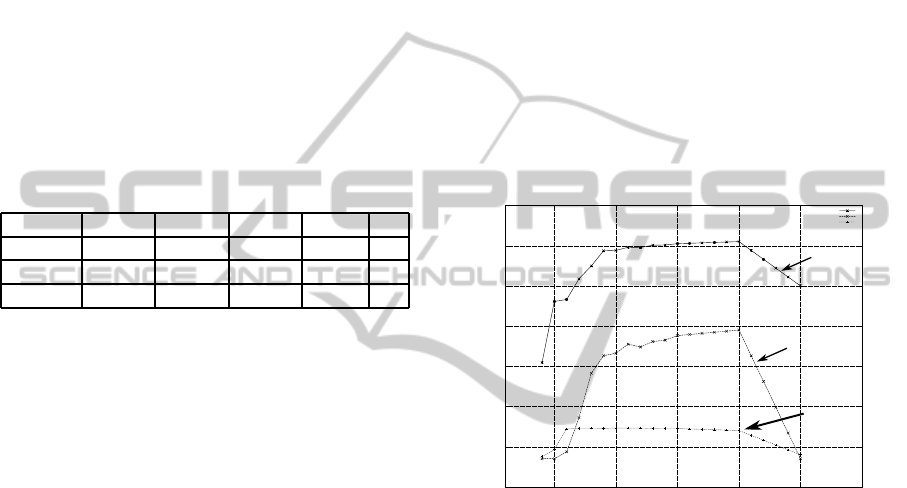
Finally , the Fig. 6 depicts the instantaneous val-
ues of the SoC, the data-rate (R
d
) and the energy har-
vested (β) during the second and third day for both
approaches. As shown, the OL-PM reactiveness al-
lows the data-rate to accurately follows the energy
AN OPEN-LOOP ENERGY NEUTRAL POWER MANAGER FOR SOLAR HARVESTING WSN
357
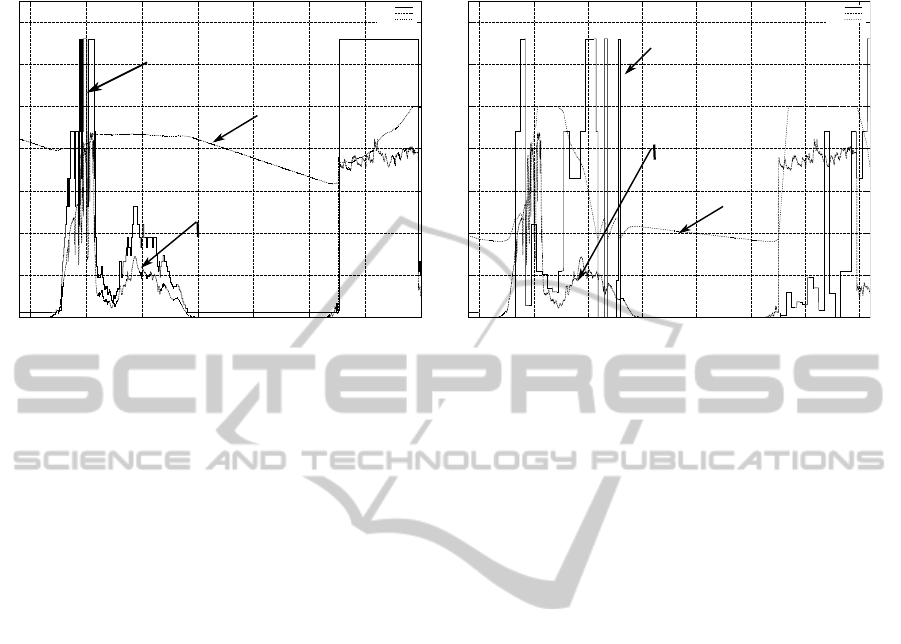
0
20
40
60
80
100
120
140
35 40 45 50 55 60 65 70
β [uA], Rd [bits/s], SoC [uAh]
time [hours]
Rd
beta
SoC
SoC
Rd
B
Open-Loop
0
20
40
60
80
100
120
140
35 40 45 50 55 60 65 70
β [uA], Rd [bits/s], SoC [uAh]
time [sec]
Rd
beta
SoC
SoC
B
Kansal
Rd
Figure 6: Execution traces of the OL-PM (n = 10) and Kansal during the second and third day.
harvested profile. In the meantime, for Kansal the
data-rate is less correlated to the β and leads to a larger
SoC drift than with our OL-PM.
6 CONCLUSIONS
In this paper, we have proposed a modeling approach
for an energy harvesting wireless sensor node. Based
on the derived model we have developed a power
manager that can dynamically adapt the duty-cycle
of the node to operate in energy neutral condition.
Experimental results have shown that up to 30% per-
formance improvement can be achieved compared to
a state of the art power management algorithm. We
have also studied the impact of the power manage-
ment reactiveness on the global system performance.
Our analysis has shown that the deviation from the en-
ergy neutrality condition is related to the reactiveness
of the power manager. Therefore, this outcome can
be used to increase the power management efficiency
by adding an adaptive control of the reactiveness. Fu-
ture works will also focus on using SoC estimation to
adapt the power manager policies. Finally, we aim to
extend our approach for different energy harvesting
system (piezoelectric, thermoelectric) and batteries.
ACKNOWLEDGEMENTS
This work is supported by the French National Re-
search Agency (ANR) project GRECO bearing refer-
ence ANR-2010-SEGI-004-04.
REFERENCES
Kansal, A., Hsu, J., Zahedi, S., and Srivastava, M. (2007).
Power management in energy harvesting sensor net-
works. ACM Transactions on Embedded Computing
Systems (TECS), 6(4):32–es.
Kansal, A., Potter, D., and Srivastava, M. B. (2004). Per-
formance aware tasking for environmentally powered
sensor networks. SIGMETRICS Perform. Eval. Rev.,
32:223–234.
Nelson, J. (2003). The physics of solar cells. Imperial Col-
lege Press London.
Shin, D., Kim, Y., Seo, J., Chang, N., Wang, Y., and Pe-
dram, M. (2011). Battery-supercapacitor hybrid sys-
tem for high-rate pulsed load applications. In DATE,
pages 875–878. IEEE.
TexasInstruments (2011). ez430-rf2500 solar energy har-
vesting kit. http://focus.ti.com/docs/toolsw/folders/p
rint/ez430-rf2500-seh.html.
Toriyama, T., Yajima, M., and Sugiyama, S. (2001).
Thermoelectric micro power generator utilizing self-
standing polysilicon-metal thermopile. In Micro Elec-
tro Mechanical Systems, 2001. MEMS 2001. The 14th
IEEE International Conference on, pages 562–565.
IEEE.
Vigorito, C., Ganesan, D., and Barto, A. (2007). Adaptive
control of duty cycling in energy-harvesting wireless
sensor networks. In Sensor, Mesh and Ad Hoc Com-
munications and Networks, 2007. SECON’07. 4th An-
nual IEEE Communications Society Conference on,
pages 21–30. IEEE.
Yi, J., Ki, W., and Tsui, C. (2007). Analysis and design
strategy of uhf micro-power cmos rectifiers for micro-
sensor and rfid applications. Circuits and Systems
I: Regular Papers, IEEE Transactions on, 54(1):153–
166.
PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems
358
