MULTI-STAGE DECISION BASED APPROACH FOR

BALANCING BI-OBJECTIVE U-SHAPED ASSEMBLY LINES

WITH ALTERNATIVE SUBASSEMBLY GRAPHS

Seren Ozmehmet Tasan

Department of Industrial Engineering, Dokuz Eylul University, Izmir, Turkey

Keywords: Assembly Line Balancing, U-shaped Assembly Line, Alternative Subassembly Graphs, Multi-stage

Decisions, Genetic Algorithms, Fuzzy Logic Controller.

Abstract: The purpose of this study is to propose an efficient way to balance the u-shaped assembly lines with

alternative subassembly graphs while minimizing the number of stations and maximizing the line efficiency.

U-shaped assembly line balancing models with alternative subassembly graphs (uALB/sb) under

consideration contains two kinds of special issues, i.e. the selection of a suitable subassembly graph among

alternatives and the balancing according to the operational precedence constrained among the tasks in the

selected subassembly graph. To deal with the multiple objectives and the special issues, first we designed

this uALB/sb as a network problem and then proposed a multi-stage decision based genetic algorithm

(mdGA). Additionally, in order to improve the performance of mdGA, we use fuzzy logic controller for

fine-tuning of genetic parameters. Finally, uALB/sb problem has been solved using the proposed solution

approach to highlight the applicability and performance of the proposed solution approach.

1 INTRODUCTION

Traditionally, an assembly line is organized as a

serial line, where stations are arranged along a

conveyor belt serially. In modern production lines

with the implementation of just-in-time (JIT)

production principles, u-shaped lines are being more

preferred among other line layouts, where serial

lines are rather inflexible and have other

disadvantages which might be overcome by a u-

shaped assembly line. The u-shaped line

compliments the JIT principle by providing more

alternatives. Namely, u-shaped lines provide more

alternatives for assigning tasks to station (operators)

than comparable serial lines because operators can

handle not only adjacent tasks, but also tasks on both

side of the u-shaped line. Further as more

advantages, u-shaped line is crowded with work

places and space is needed few. Operators work

together in u-shaped line and it can make

communication easier and trust each other.

In u-shaped lines, the stations are arranged along

a rather narrow U, where both legs are closely

together, and the entrance and the exit of the line are

on the same position. Stations in between those legs

may work at two segments of the line facing each

other simultaneously. This means that the

workpieces can revisit the same station at a later

stage in the production process without changing the

flow direction of the line. This can result in better

balance of station loads due to larger number of

task-station combinations where operators can

handle adjacent tasks as well as tasks on both sides

of the u-shaped line. Another advantage of u-shaped

lines is that they simultaneously maximize both the

use of operational workspace and operator

communication and trust, such that machines take up

less space and workers are closer to one another.

Besides improvements with respect to job

enrichment and enlargement strategies, a u-shaped

line design might result in a better balance of station

loads due to the larger number of task-station

combinations (Miltenburg & Wijngaard, 1994;

Monden, 1998; Scholl & Klein, 1999). Usually, in a

u-shaped assembly line balancing model, researchers

deal with the allocation of the tasks among stations

so that the precedence relations are not violated and

given objective functions is optimized. Additionally

at the same time, there mostly exits alternative ways

of doing these tasks, e.g., there may be two

alternative ways to perform a cable assembly task.

This kind of disjunctive assembly line balancing

334

Ozmehmet Tasan S..

MULTI-STAGE DECISION BASED APPROACH FOR BALANCING BI-OBJECTIVE U-SHAPED ASSEMBLY LINES WITH ALTERNATIVE SUBASSEM-

BLY GRAPHS.

DOI: 10.5220/0003942903340342

In Proceedings of the 2nd International Conference on Pervasive Embedded Computing and Communication Systems (PECCS-2012), pages 334-342

ISBN: 978-989-8565-00-6

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

problem has been receiving attention of researchers

since it has been first identified by Capacho &

Pastor (2005), However, all of the researchers

considered only single model with serial lines such

as Capacho & Pastor (2006, 2008), and Scholl et al.

(2009). In this study, we considered U-shaped

assembly line balancing models with alternative

subassembly graphs (uALB/sb). The problem under

consideration contains two kinds of special issues,

i.e. the selection of a suitable subassembly graph

among alternatives and the balancing according to

the operational precedence constrained among the

tasks in the selected subassembly graph.

Traditionally to solve these kinds of u-ALB/sb

problems, researchers first tries to identify the best

alternative in the form of one precedence diagram

and finally balance this problem using only this

precedence diagram. However, most of the time,

researchers are giving the utmost importance to the

balancing rather than the selection of alternatives.

Particularly, the disjunctive relationship between

these two problems is often neglected and they are

solved separately in a hierarchical manner.

Nevertheless, by using the traditional hierarchical

approach, the u-ALB/sb problem can lose its

integrity since the researchers are eliminating some

features of the whole problem before balancing

procedure.

To maintain the integrity of the u-ALB/sb

problem, in this study, an integrated monolithic

approach, which considers selection together with

balancing, is proposed. Particularly, a multi-stage

decision based genetic algorithm (mdGA) approach

is constructed in order to consider it as an exclusive

problem while using a specific decoding procedure.

The rest of the paper is organized as follows; In

Section 2, the background information on the main

features of u-ALB/sb are introduced. In Section 3,

overall methodology of the proposed mdGA

approach and its general features are discussed in

detail. In Section 4, in order to evaluate the

performance, the proposed mdGA approach is

demonstrated on some problem instances, and the

experimental results are analyzed. Finally, the

concluding remarks and future research directions

are given in the last section.

2 BALANCING U-SHAPED

ASSEMBLY LINES WITH

ALTERNATIVE SUBASSEMBLY

GRAPHS

The assembly line balancing problems are usually

represented with precedence relations, which can be

transformed into a more visual form as precedence

diagrams. Precedence diagrams only model

conjunctions (AND relations), not disjunctions (OR

relations). However, in real-life, we usually come

across assembly line balancing problems with

alternative subassembly graphs. In this section, we

considered uALB models with alternative

subassembly graphs (uALB/sb). The uALB is a

generalization of assembly line balancing problems

and hence belongs to the class of NP-hard problems.

Hence its decision version uALB/sb is NP-complete.

As a disjunctive network optimization problem, in

uALB, each subassembly graph represents

subassembly, which is the alternative way for

performing a subset of task or tasks and each node

represents the tasks of a subassembly. The uALB/sb

model consists of i=0,1,…, I+1 subassemblies and

the precedence relations between each subassembly

are taken into consideration according to the

network structure. In each subassembly i, there are

k=0,1,…, K+1 alternative ways to perform that

subassembly. Fig.1 illustrates the conceptual

network for assembly line balancing problem with

alternative subassembly graphs.

In each alternative subassembly k, there are

j=0,1,…, J+1 tasks with precedence relations, where

ikj

denotes the variable processing time of task j in

alternative k of subassembly i. Particularly, the

detailed concepts of subassembly graphs and task

are given in Fig.2. In this model, the activities are

interrelated by two kinds of constraints; the

precedence constraints which are known from

traditional uALB, force a task no to be started before

all its predecessors have been finished and the new

constraints force a subassembly no to be started

before all its predecessors have been finished.

Specifically, the uALB/sb model considered in

this study can be defined by the following

assumptions:

A1. The problem consists of multiple

subassemblies.

A2. There exists alternative ways to perform

each subassembly.

A3. Each subassembly alternative contains

number of tasks with known processing

time

A4. The assembly line is used to assemble

one homogeneous product in mass

quantities.

A5. The line is U-shaped, paced line with

fixed cycle time and there are no feeder

lines.

MULTI-STAGE DECISION BASED APPROACH FOR BALANCING BI-OBJECTIVE U-SHAPED ASSEMBLY

LINES WITH ALTERNATIVE SUBASSEMBLY GRAPHS

335

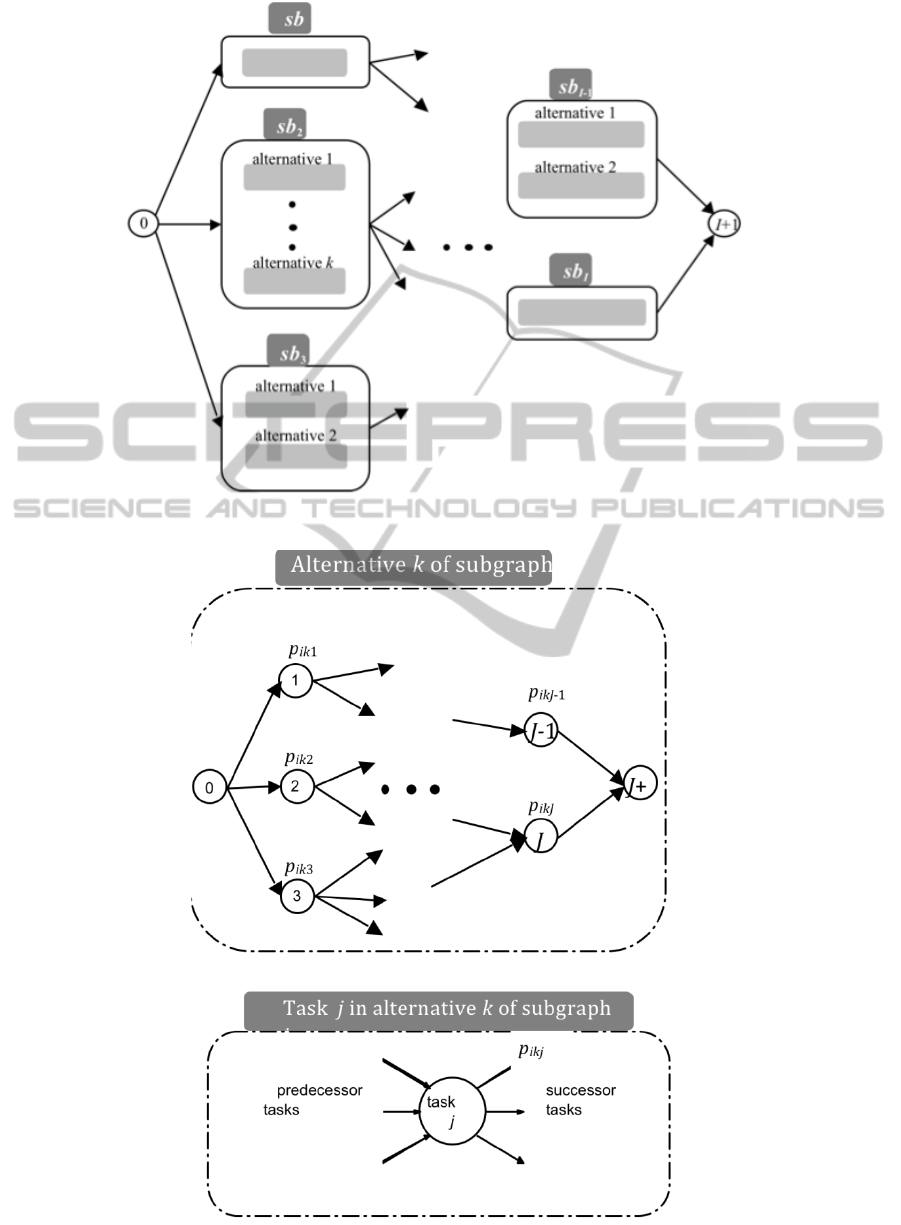
Figure 1: General concept of an assembly line balancing problem with alternative subgraphs.

Figure 2: Subgraph and task concepts.

PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems

336

A6. The processing times of tasks are

deterministic.

A7. All stations are equally equipped with

respect to machines and workers.

A8. A task cannot be split among two or

more stations.

A9. There are no assignment restrictions

besides the precedence constraints.

A10. All stations can process any one of the

tasks and all have the same associated

costs.

A11. The processing time of a task is

independent of the station and

furthermore, they are not sequence

dependent.

A12. The problem model allows for the

forward and backward assignment of

tasks to stations; for example, the first

and last tasks of an assembly can be

placed in the same station on a u-shaped

line, but not on a serial line system.

A13. The objectives are to minimize the

number of stations and maximize the line

efficiency.

For network complexity of alternative k of

subassembly graph i, the following normalized

complexity measure, C

over [0,1] is adapted from

Browning & Yassine (2010);

max max

max

44 4

(2)

′

−+

−

(1)

where A’

max

represents the number of precedence

relationships (non-redundant arcs), and N

max

represents the number of nodes. The network

complexity of alternatives for subassembly graph i is

defined by

123,

(, , )

iiii iK

CCCC C= K

. In this study,

instead of using a composite network complexity

such as using subassembly graph complexity

averages, a vector of subassembly graph complexity

measures,

123,

(, , )

CCCC C= K

will be used as the

disjunctive network complexity measure.

3 MULTI-STAGE DECISION

BASED GA APPROACH

The foundation of mdGA lies in the multi-stage

decision making problem (mdmP) described as one

process, which can be divided into several stages. At

each stage, there exist a set of similar decision to be

made that is called state. In the past decade this

problem has captured the interest of researchers,

which resulted in formation of various solution

approaches such as mdGA. In the original mdGA

approach, first the problem is constructed; second

this problem is divided into several stages; third

corresponding states are assigned to these stages;

and finally an optimum state for each stage is found

using genetic search procedure. For more

information about the original mdGA, readers may

refer to Osman et al. (2005), Gen & Zhang (2006)

and Gen et al. (2008). In this research, a GA

approach will be constructed in order to solve the

disjunctive network problems efficiently. Since there

exist two sub-problems, i.e., selection and balancing,

mdGA is going to be developed to reflect the sub-

problems together in the exclusive problem.

However, since the u-ALB/sb problems consist

of two sub-problems, a new kind of mdGA has been

proposed. In the proposed mdGA approach, first the

selection sub-problem is divided into the stages;

second the corresponding states are assigned to these

stages; third the scheduling sub-problem is

constructed states; and finally the newly constructed

scheduling sub-problems is solved by using genetic

search procedure. The overall procedure of the

proposed mdGA approach is planned as follows:

overall procedure: mdGA for u-ALB/sb problems

input: problem data, GA parameters

output: the best balance

begin

t ← 0;

initialize P( t ) by multistage-based and priority-

based encoding routines;

evaluate P( t ) by priority-based decoding routine;

while (not terminating condition) do

create C( t ) from P( t ) by crossover routine;

create C( t ) from P( t ) by mutation routines;

evaluate C( t ) by priority-based decoding routine;

if t > u then

regulate adaptive GA parameters p

and p

using fuzzy logic parameter tuning routine;

select P( t + 1) from P( t ) and C( t ) by selection

routine;

t ← t + 1;

end

output the best balance;

end

* P( t ) and C( t ) represents parent and offspring in current

generation t, respectively.

* u represents the number of generations needed to warn-up the

genetic search procedure.

MULTI-STAGE DECISION BASED APPROACH FOR BALANCING BI-OBJECTIVE U-SHAPED ASSEMBLY

LINES WITH ALTERNATIVE SUBASSEMBLY GRAPHS

337

3.1 Genetic Representation and

Initialization

In the proposed mdGA, an individual, which is

composed of two chromosomes, i.e. multistage-

based chromosome for representation of

subassembly graph alternatives and priority-based

chromosome for representing node sequences, is

constructed (see Figure 3). The multistage-based

chromosome is a fixed-length direct chromosome

representation. However, the priority-based

chromosome is variable-length indirect chromosome

representation. To develop a genetic representation,

there are three main phases, i.e. creating stages,

creating a feasible disjunctive network, designing

the schedule.

Figure 3: Genetic representation for a u-ALB/sb problem.

Phase 1: Creating stages

step 1.1: Generate a random number to each

alternative subassembly graph using multistage-

based encoding procedure

In order to create multistage-based chromosome,

permutation encoding given in Figure 4 is used. For

each subassembly graph, a random integer number

between [1, K

) is generated. In the multistage-based

chromosome, the position is used to denote a

subassembly graph ID and the content of the gene v

( ) is used to denote the selected alternative way to

perform this subassembly graph K

(see Figure 3).

procedure: permutation encoding routine

input: number of subgraphs I, number of alternatives for

subgraphs i, K

output: multistage-based chromosome v

( )

begin

for i=1 to I

(i) ←0;

for i=1 to I

(i) ← random[1, K

];

output multistage-based chromosome v

()

end

Figure 4: Permutation encoding procedure for creating a

multistage-based chromosome.

Phase 2: Creating a feasible precedence network

step 2.1: Generate a random priority to every node

in selected alternative subassembly graph using

priority-based encoding procedure

Using the multistage-based chromosome, a

network model can be constructed using priority-

based chromosome. In order to create a priority-

based chromosome, an indirect representation

scheme called priority-based encoding method is

used. Figure 5 presents the procedure for the

priority-based encoding procedure where v

( ) is a

priority value and m is number of total nodes in all

subassembly graphs. In the priority-based

chromosome, the position is used to denote a node

ID and the priority value v

( ) is used to denote the

priority associated with the node. The value of a

gene is an integer exclusively within [1, m). The

larger the integer value is the higher the priority

becomes (see Figure 3).

procedure: priority-based encoding routine

input: number of subgraphs I, multistage-based

chromosome v

( )

output: priority-based chromosome v

( )

1 ( )

() 0;

(())do

random(1, ( ));

(()0)

() ;

ρρ

←

≤

←

←+

jvi

begin

for to

while

if then

end

output priority-based chromosome v

( )

end

Figure 5: Priority-based encoding procedure for creating a

priority-based chromosome.

Phase 3: Designing the balance

step 3.1: Decode a feasible node sequence that

satisfies the precedence constraints using priority-

based decoding procedure.

In order to decode the priority-based

chromosome generated by encoding procedure in

step 2.1, a special two-step priority-based decoding

procedure is used for accommodating the

characteristics of uALB/sb. In this procedure, first

the priorities of each task are used to create a

feasible task sequence that satisfies the precedence

constraints in the uALB/sb model. Later, using the

feasible task sequence found in the first step, tasks

are assigned to stations. Figure 6 presents the two-

step priority-based decoding procedure.

step 3.2: Draw a Gantt chart for this balance

PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems

338

Using the balance found in step 3.1, the Gantt

chart for the balance can be easily designed.

3.2 Genetic Operators

Since an individual is composed of two parts and

also the priority-based chromosome is variable in

length, the usage of genetic operators, i.e. crossover,

mutation and selection, becomes more complicated.

The objective of applying crossover operator, which

generates new solutions (offsprings) using parts

contained in different solutions of the current

population (parents), is to guide the search toward

promising regions of the feasible domain while

maintaining some level of diversity in the

population. Crossover operator was used only for the

priority-based chromosome representation. The

position-based crossover (PMX) was adopted

(Syswerda, 1991). Essentially, it takes some tasks

from one parent at random and fills vacuum position

with tasks from the other parent by a left-to-right

scan. Since priority-base chromosome is variable in

length, the parents with different lengths are used in

PMX operation, which may result in offsprings with

different lengths.

As a mutation operator, for multistage-based

chromosome random mutation is used and after that

for priority-based chromosome swap mutation (SM)

is used (Syswerda, 1991). In random mutation, a

random gene is randomly selected and the content of

this gene is randomly generated between the integer

values of [1, K

] are used. In swap mutation two

positions are selected at random and their contents

are swapped is used.

To eliminate the drawback of classic selection

operators, diversity preserving selection (DPS)

operator is used in this research (Bosman &

Thierens, 2003).

Like elitist selection, DPS preserves the best

chromosome in the next generation and overcome

the stochastic errors of sampling. With the elitist

selection, if the best individual in the current

generation is not reproduced into the new

generation, one individual is randomly removed

from the new population and the best one is added to

the population. However, DPS dynamically adjust

itself to be more elitist when population’s diversity

is high and less aggressive (less elitist) when the

population includes solutions that are increasingly

similar. In DPS procedure, the population diversity

measure is represented by D where D ∈ [0,1]

increases with the diversity of the population.

procedure 1: priority-based decoding routine (step 1:

creating task sequence)

input: number of tasks n, chromosome v(j)

output: a task sequence T

begin

,sT

←

∅←∅

;

0, 0nj

←

;

while (j ≤ n) do

(

)

Suc

j←

;

(

)

Prec

j←

;

(

)

{

}

arg maxjvjjs

←

∈

;

←

;

TTj

←

∪

;

←

end

output

a task sequence T

end

procedure 2: priority-based decoding routine (step 2: task

to station assignment)

input: processing time t

, chromosome v(j), the task

sequence T

output: number of stations m, efficiency E, schedule S

begin

0, =1, 2, , ;

0, 0, 0, 0, 0;

tj n

Si m

jmEV EV

←

←←←← ←

for j = 1 to n

while (

()

≤ c

) do

;

() () ;

iij

tS tS t

←

;

SUM S

SUM T

;

/( );

;

Et mc

uum

←

←++

←

end

output

number of stations m, efficiency E,

end

Figure 6: Two-step priority-based decoding procedure for

designing a balance.

3.3 Parameter Tuning Strategy by FLC

In this research, a fuzzy logic controller (FLC)

concept of Wang et al. (1997) is used to regulate the

MULTI-STAGE DECISION BASED APPROACH FOR BALANCING BI-OBJECTIVE U-SHAPED ASSEMBLY

LINES WITH ALTERNATIVE SUBASSEMBLY GRAPHS

339

Figure 7: Coordinated strategies of FLC and mdGA.

parameter values as a auto-tuning strategy in the

proposed mdGA. At the beginning of the genetic

search procedure of mdGA, the parameter values for

crossover rate (p

) and mutation rate (p

) are kept

constant for a predetermined period of time (u),

which represents the number of generations needed

to warm-up the genetic search procedure before

starting the FLC. After u

generation, FLC auto-

tuning strategy recalculates the values of p

and p

while considering the changes in the average fitness

value in each generation. Thus by fine-tuning of

these parameters, much computational time can be

saved and the search ability of mdGA in finding

global optimum can be improved more than the

conventional mdGA without FLC. The main idea of

the concept used in this research consists of two

FLCs; crossover FLC and mutation FLC that are

implemented independently to adaptively regulate

the crossover ratio and mutation ratio during the

genetic search process (see Figure 7). The inputs of

mutation fuzzy controller are the same as the

crossover fuzzy controller, and the output of which

is changed by the mutation ratio.

4 COMPUTATIONAL

EXPERIMENTS

To investigate the performance of the proposed

mdGA approach for solving uALB/sb,

computational experiments have been performed on

a set of problems, which consist of different number

of subassemblies, different disjunctive network

complexity measures and different cycle times.

Since there exists no benchmark problem set in

literature, five problems were randomly constructed

to form the uALB/sb instances. The first two

problems have subassemblies with low network

complexity (C

<0.6) and the following three

problems have subassemblies with high network

complexity (C

≥0.6). Table 1 summarizes the

information about problem instances.

In the computational experiments, the proposed

mdGA is compared to two traditional hierarch

methods, which solve the uALB/sb in two steps. The

first step includes the selection of alternative

subassemblies with minimum number tasks in order

to form one precedence diagram and the second step

includes solving this precedence diagram. After the

selection of subassemblies, to solve the u-shaped

assembly line balancing problem, the first method

uses IP and the second method uses priority-based

GA proposed by Gen et al. (2008).

For the computational experiments, the following

values for mdGA parameters are used: Population

size: popSize =1000, Crossover probability: p

=0.75, Mutation probability: p

=0.2, and

Terminating condition: Maximum number of

generations: maxGen = 100 or Convergence limit:

conLim=40. In mdGA, the values of p

and p

are

adaptively regulated by FLC during overall

procedure. For each problem set, the traditional

hierarchic method with priority-based GA and the

proposed mdGA approaches were run 10 times with

parameters mentioned and compared with the

traditional hierarchic method with IP solved in

Lindo. The results are summarized in Table 2.

Based on the computational experiments while

considering minimization of the number of stations

and maximization of the line efficiency as

objectives, it can be clearly seen that for uALB/sb

with shorter cycle times (i.e. 14 and 33), lower

number of subassemblies (i.e. 2 and 3) and lower

disjunctive complexities, all methods performed

PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems

340

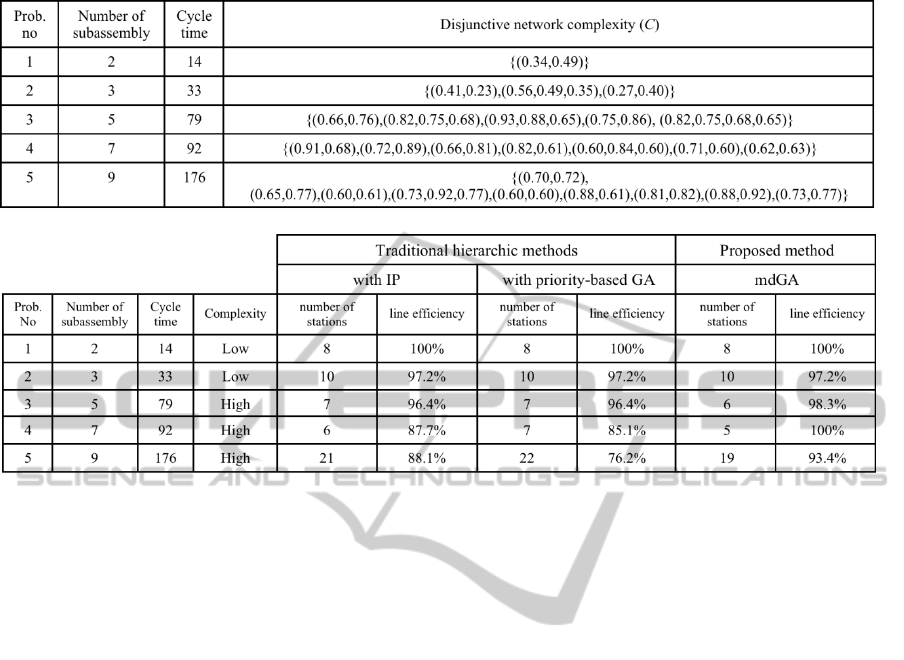
Table 1: Summary of uALB/sb instances.

Table 2: Computational results of uALB/sb.

similarly. However, in other problem instances with

longer cycle times and higher disjunctive

complexities, the proposed mdGA methods

outperformed the other traditional hierarchic

methods for both objectives. Particularly, this is due

to the increased number of possible task-workstation

assignments during mdGA while considering

alternative subassemblies simultaneously.

Overall, the proposed mdGA performs well for

all uALB/sb instances

5 CONCLUSIONS

In a highly competitive environment with rapidly

changing requirements, researchers have to consider

several alternatives when dealing with assembly line

balancing problems. In these problems, it is expected

that alternative networks under a single disjunctive

network umbrella will deliver benefit, which is not

achievable, if the alternative networks were solved

independently. Particularly, most of the time,

researchers are giving the utmost importance to the

balancing rather than the selection of the

alternatives. However, the relationship between

these two problems is often neglected and they are

solved separately in a hierarchical manner, which

usually result in the loss of network integrity.

Therefore, to maintain the integrity, there is a need

for a solution method that can effectively handle and

solve this kind of problems.

For this purpose, the contribution of this research

is threefold. First, the u-ALB/sb problem, which

consists of alternative selection and balancing sub-

problems, were defined in detail. Second as a

contribution to solution method, a new mdGA

approach was proposed to handle and solve this kind

of problems, while maintaining the integrity. In the

proposed mdGA, first, two chromosomes, i.e. fixed-

length multistage-based chromosome for

representation of subassembly graph alternatives and

variable-length priority-based chromosome for

representing task sequence, were introduced in order

to form an individual that is representing a problem

solution. Following, advanced genetic operators

adapted to the specific individual structure and the

characteristics of the u-ALB/sb problem were used.

Besides, FLC based auto-tuning strategy was used to

regulate the genetic parameters during the genetic

search process of mdGA. Third as a contribution to

problem area, in order to accommodate the

characteristics of uALB/sb, a new two-step priority-

based decoding procedure was used. Furthermore, in

order to illustrate the performance of the proposed

mdGA approach, a set of problems for u-ALB/sb

were generated and the results found by the

proposed mdGA approach were compared with two

traditional hierarchic methods. From the solution

performance perspective, computational experiments

showed that the proposed mdGA approach is

effective in finding good solutions for both problem

types, especially for problems with high disjunctive

MULTI-STAGE DECISION BASED APPROACH FOR BALANCING BI-OBJECTIVE U-SHAPED ASSEMBLY

LINES WITH ALTERNATIVE SUBASSEMBLY GRAPHS

341

network complexities, while maintaining structural

integrity of the problem by considering alternative

subassembly graphs simultaneously. There are

various future research directions related to this

research. In order to illustrate performance of the

proposed solution approach, new, adapted and

adopted solution approaches can be constructed to

solve the u-ALB/sb problems and their

performances can be compared with the proposed

mdGA. Furthermore, the proposed approach can be

applied to real world problems that are usually

complex and large.

REFERENCES

Bosman P. A. N. & Thierens D., 2003. The Balance

between Proximity and Diversity in Multiobjective

Evolutionary Algorithms. IEEE Transactions on

Evolutionary Computation, vol. 7, no. 2.

Browning T. R. & Yassine A. A., 2010. Resource-

constrained Multi-project Scheduling: Priority Rule

Performance Revisited, International Journal of

Production Economics, vol. 126, no. 2, pp. 212-228.

Capacho L. & Pastor R., 2005. ASALBP: The Alternative

Subgraphs Assembly Line Balancing Problem.

Working paper IOC-DP-P 2005-5. Universitat

Politecnica de Catalunya.

Capacho L. & Pastor R., 2006. The ASALB Problem with

Processing Alternatives Involving Different Tasks:

Definition, Formallization and Resolution. Lecture

Notes in Computer Science 3982, pp. 554-563.

Capacho L. and Pastor R., 2008. ASALBP: The

Alternative Subgraphs Assembly Line Balancing

Problem. International Journal of Production

Research, vol. 46, pp. 3503–3516.

Gen M. & Zhang H., 2006. Effective Designing

Chromosome for Optimizing Advanced Planning and

Scheduling, Dagli, C.H. et al. ed.: Intelligent

Engineering Systems through Artificial Neural

Networks, vol.16, pp.61-66, ASME Press.

Gen M., Cheng R., & Lin L., 2008. Network Models and

Optimization: Multiobjective Genetic Algorithm

Approach, Springer.

Miltenburg J. & Wijngaard J., 1994. The U-line Line

Balancing Problem, Management Science, vol. 40, no.

10, pp. 1378-1388.

Monden Y., 1998. Toyota Production System––An

Integrated Approach to Just-in-time, 3rd ed.

Dordrecht: Kluwer.

Osman M. S., Abo-Sinna M. A. & Mousa A. A., 2005. An

Effective Genetic Algorithm Approach to

Multiobjective Resource Allocation Problems, Applied

Mathematics and Computation, vol.163, pp.755-768.

Scholl A. & Klein R., 1999. Balancing Assembly Lines

Effectively—A Computational Comparison. European

Journal of Operational Research, vol. 114, pp. 50–58.

Scholl A., Boysen N., & Fliedner M., 2009. Optimally

Solving the Alternative Subgraphs Assembly Line

Balancing Problem, Annals of Operations Research,

vol. 172, no. 1, pp. 243-258.

Syswerda G., 1991. Scheduling Optimization using

Genetic Algorithms, 332-349 in Davis, L. Ed.:

Handbook of Genetic Algorithms, Van Nostrand

Reinhold, New York.

Wang P. Y, Wang G. S., & Hu Z. G., 1997. Speeding up

the Search Process of Genetic Algorithm by Fuzzy

Logic, Proceedings of European Congress on

Intelligent Techniques and Soft Computing, pp. 665-

671.

PECCS 2012 - International Conference on Pervasive and Embedded Computing and Communication Systems

342