POWERTRAIN SLIDING MODE CONTROL IN SHEV FOR

IMPROVEMENT OF FUEL ECONOMY AND ESS LIFETIME

Xi Zhang and Chengliang Yin

National Engineering Lab for Automotive Control Electronics, Shanghai Jiao Tong University, Shanghai, China

Keywords: Sliding Mode Control, SHEV, Battery Lifetime Extension, Speed Control, Torque Control.

Abstract: This paper proposes a powertrain sliding mode control strategy for a series hybrid electric vehicle (SHEV)

aimed at improving fuel economy and energy storage system (ESS) lifetime. An ESS charging curve

considering positive factors for ESS lifetime extension is predetermined, and two robust sliding mode

controllers using the fixed boundary layer technology are designed. One is in charge of engine speed

control, and the other is for torque control. Thus the powertrain control system could not only reduce

emissions due to engine efficiency enhancement but extend ESS lifetime. Finally, simulation results using

ADVISOR confirm validity of the proposed strategy.

1 INTRODUCTION

Electric power as the only propulsion power for a

series hybrid electric vehicle (SHEV) comes from

the ESS and the engine/generator set that converts

the energy from fuel into electricity. In SHEV,

Engine optimal operation region could be located

properly due to the particular structure.

Recently, appropriate control of the SHEV

powertrain for emission reduction has been a

research hotspot. A modified instantaneous

equivalent consumption minimization strategy

(ECMS) into the SHEV powertrain control system

was introduced (Plsu and Rizzoni, 2005). Wang et

al., (2008) introduced a simulated annealing (SA)

algorithm to optimize the operational parameters for

SHEV fuel economy and emissions. Unfortunately,

these SHEV powertrain control strategies fail to

sufficiently address the highly nonlinear parameter

variations and sudden external disturbances during

the vehicle operation.

Sliding mode control (SMC) is very suitable for

automotive applications due to its low sensitivity to

disturbances and plant parameter variations

(Kachroo and Tornizuka, 1996; Utkin et al., 2009).

In this paper, powertrain controller design uses the

chattering-free fixed-boundary-layer technology for

chattering elimination. To locate the engine

operation in the optimal efficiency region, two

proposed sliding mode controllers responsible for

engine speed and torque respectively work together

due to the simultaneous speed and torque magnitude

constraints in such an area.

So far, few manufacturers concern the systematic

electrical solutions for battery lifetime extension

under the present battery technology. It’s available

to analyze some stress factors which induce ageing

and influence the rate of ageing (Svoboda, 2007).

Consequently, comparison between two ageing

processes with a couple of different stress factors

(e.g. SOC, charge rate, temperature, etc.) is possible

as long as other operating conditions are similar.

Some problems which affect battery lifetime

such as surge current, persistent high power, low

SOC and so on in conventional powertrain control

have to be concerned. To solve these, this paper

presents an ellipse-like-based battery charge

scenario. When the engine starts, the battery keeps

charging at a high rate from the low SOC level, and

its SOC increases fast. The charge current gradually

drops to zero when the SOC approaches to the

predetermined maximum level. The chaotic and fast-

variable current almost disappears, which is very

good for battery lifetime extension.

Finally, simulation results by modifying the

original SHEV model in Advanced Vehicle

Simulator (ADVISOR) confirm that the proposed

strategy is valid and efficient.

235

Zhang X. and Yin C..

POWERTRAIN SLIDING MODE CONTROL IN SHEV FOR IMPROVEMENT OF FUEL ECONOMY AND ESS LIFETIME.

DOI: 10.5220/0003945602350238

In Proceedings of the 1st International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2012), pages 235-238

ISBN: 978-989-8565-09-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

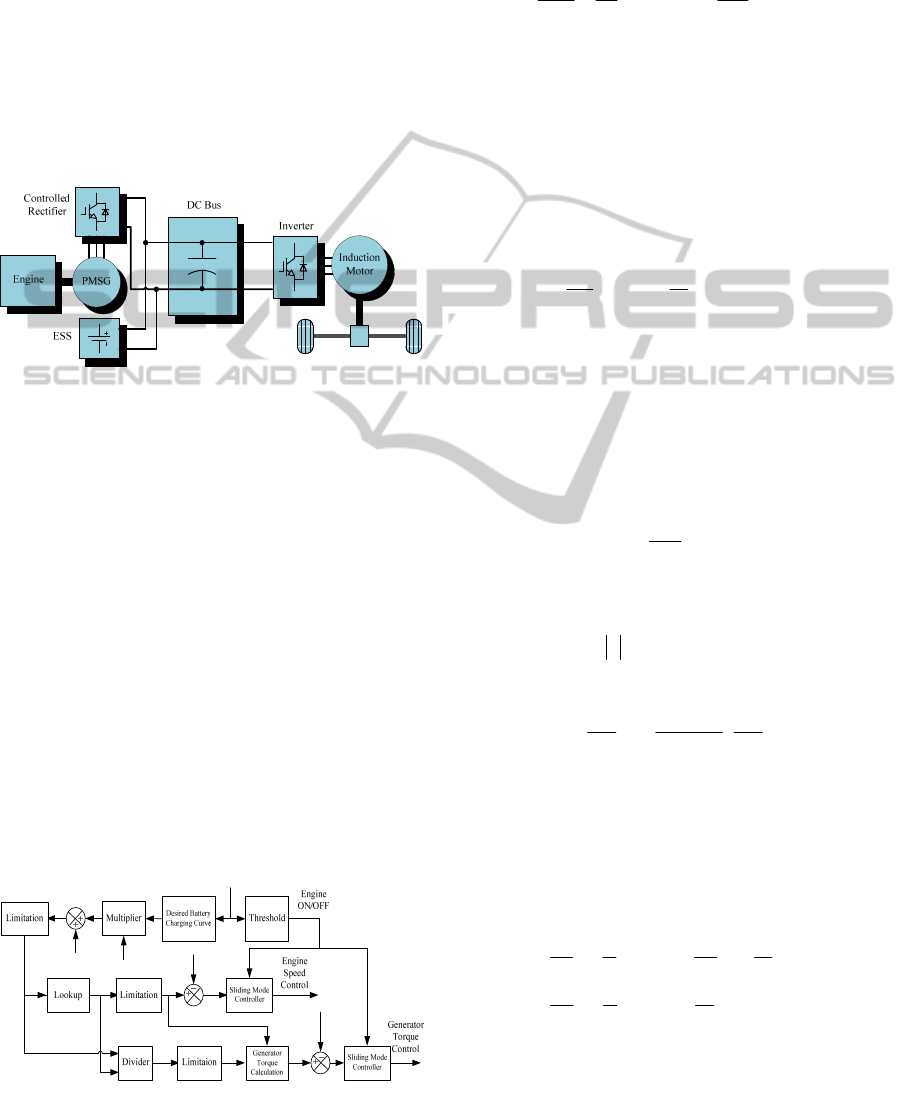
2 POWERTRAIN STRUCTURE

The structure of the studied SHEV powertrain is

shown in Figure 1. An internal combustion engine

(ICE) linked to a permanent magnet synchronous

generator (PMSG) provides main power in hybrid

mode. The ESS (battery pack) serves as the only

power source in the pure-electric-vehicle (EV) mode

and also absorbs the energy in the regeneration

process (braking or deceleration). In addition, the

battery pack will be charged by the engine when its

state of charge (SOC) drops to a predetermined

level, as determined by the control strategy.

Figure 1: Studied SHEV powertrain structure.

3 POWERTRAIN CONTROLLER

DESIGN

The block diagram of the proposed powertrain

control system is shown in Figure 2. Definitions of

variables in this figure are given as follows:

SOC

state of charge;

, battery output voltage;

calculated battery charging current;

, load demand;

, required power for battery charging;

, engine

output power with limitations;

, calculated engine

speed;

, calculated engine speed with limitations;

, actual engine speed;

, calculated engine

torque;

, calculated engine torque with limitations;

, final required generator torque; and

, actual

generator torque.

Figure 2: Proposed powertrain control system.

3.1 Engine Speed Control

The engine operation state function can be expressed

below

max

()

uT T

tJ nJ

=−

(1)

where

max

()

stands for the maximum torque at

speed

≈

denotes speed ratio between the

engine and generator,

is moment of inertia of the

engine/generator set, and

represents the engine

throttle angle (considered as the control variable)

and could be delineated as follows.

()

uAu B

−

′

=−

(2)

where

=−

max

()

=−

, the subscript n

stands for the nominal value, and

′

is considered as

a new control variable.

Let the sliding surface

eet

∫

, where

−

and

is a constant, and the new control

variable can be obtained using the fixed boundary

layer sliding mode control technology, expressed

below

()

(( ) ) (( ),,)

msat s

θω λ

ηαωφ

′

−+++

(3)

where

is a predetermined constant and

satisfies

<−



;

is the width of sliding

mode layer. The error function

()

is given by

max

()

eE G Gn

sEs

nJ T nJ

θω

=− + ⋅

(4)

3.2 Engine/Generator Torque Control

The state functions of the PMSG can be delineated

as follows:

(5)

where

and

, stator direct-axis and quadrature-

axis currents;

and

, stator direct-axis and



SOC

Gtrqq

qGd m

dGq

TKi

tL L L

tL L

ωλ

⎧

⎪

−− + −

⎨

⎪

=− + −

⎪

⎩

SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems

236

quadrature-axis inductances;

, flux of the

permanent magnet;

, stator winding resistance;

≈

, generator speed (replaced by

in the

following analysis);

trq

, torque constant;

and

, stator direct-axis and quadrature-axis voltages,

as control variables in the system.

Let the sliding surface

d, 1,2

iiii

se eti

=+ =

∫

where

1 qq

eii=−

, and

2 dd

eii=−

. Similar to

derivation process in engine speed control, new

controls can be obtained as

(6)

and

(7)

where

0 ( 1,2)

is a predetermined constant and

satisfies

(1,2)

ii i i

ss s i

<− =



, and

0 ( 1,2)

are

the widths of the two sliding mode layers.

Derivation of the error function is similar to that in

engine speed control.

Thus, the required stator direct-axis and

quadrature-axis voltages can be finally obtained to

guarantee desired generator torque.

3.3 Battery Charging Scenario Design

Although several options (e.g., parabola, ellipse,

line, trigonometric, etc.) exist for such a charging

scenario, only ellipse could satisfy all the fore-

mentioned requirements. In the meantime, the

ellipse curve is easy to calculate and easy to be

implemented in microprocessors. Consequently it is

possible to realize it in real time and real

applications. In this paper, a combination of line and

ellipse (see Figure 3) is eventually selected because

one wants the battery SOC to reach the “healthy”

low threshold SOC1 in the beginning phase (Phase

I) and then approaches to the maximum value

SOCmax in Phase II.

It has to be noted that the engine may not meet

the calculated power requirement that is the sum of

battery charging power and the peak driving power

demand at some instants. Thus constraints have to be

added.

When

the calculated engine power is located in

the high-efficiency region, the battery can be

charged along the pre-set curve. If the calculated

engine power exceeds the high-efficiency region, the

driving power demand is first satisfied while the

battery charging points may not lie on the pre-set

one. Whichever case happens, the dynamics of the

entire SHEV will not be influenced at all, the engine

always runs in the optimal region, and the

requirement of choosing a high-power engine could

also be avoided.

Figure 3: Desired battery charging curve.

4 SIMULATION RESULTS

This study employs ADVISOR for verification. The

original SHEV model is modified to embed the

proposed control system into the powertrain. In this

simulation, a Geo Metro 1.0L engine is selected. A

PMSG rated with 41kW-power and 95%-efficiency

is linked with the engine, and an induction motor

rated with 75kW-power and 95%-efficiency acts as a

traction motor. 100 Ovonic M70 cells compose the

battery pack where 50 are in series and 2 in parallel.

The inverter and controlled-rectifier both own the

structure of three IGBT/diode bridges.

The Orange County Cycle (OCC) is chosen as

the drive cycle for analysis. This is because the OCC

comprises of considerable acceleration/deceleration

processes and is capable of sufficiently validating

SHEV advantages on possible improvement of

system efficiency. The constants in the above

analysis are set as follows:

3540,

650,

2.03,

2.46,

min

0.6,SOC =

max

0.8,SOC =

0.68.SOC =

Figure 4 shows the engine operation efficiency

map. It is obvious from comparison between Figure

4(a) and 4(b) that most operation points using the

proposed strategy are located in the optimal region

while most points using the conventional method are

beyond such an area.



()

11 11

11 111

()

( ) ( ( ), , )

uX e

FX msat X s

θλ

=− + +

−+



()

22 22

22 222

()

( ) ( ( ), , )

uX e

FX msat Xs

θλ

αφ

=− + +

−+

maxB

SOC

min

SOC

max

SOC

POWERTRAINSLIDINGMODECONTROLINSHEVFORIMPROVEMENTOFFUELECONOMYANDESS

LIFETIME

237

(a) Conventional method

(b) Proposed method

Figure 4: Engine operation efficiency map.

The battery current curves using the

conventional and proposed methods respectively are

depicted in Figures 5(a) and 5(b). It is clear that

chaotic and surge currents using the proposed

method in the normal (engine is ON) mode almost

disappeared compared to those using the

conventional method, which does good to the battery

lifetime extension.

(a) Conventional method

(b) Proposed method

Figure 5: Battery current during OCC.

Table 1 gives some index including MPG,

emissions, efficiency resulting from simulation

using two methods. It is obvious that the proposed

method performs better fuel economy, lower

emissions and higher efficiency.

Table 1: Performance comparison between two methods.

Method

Index

Conventional

Method

Proposed Method

MPG 37.8 40.9

Emissions

(g/mile)

HC:0.783,

CO:3.234,

NOx:0.838

HC:0.781,

CO:2.158,

NOx:0.820

Average Engine

Efficiency

0.301 0.322

Overall System

Efficiency

0.0720 0.0782

5 CONCLUSIONS

This study presents two sliding mode controllers for

SHEV powertrain on basis of a predetermined

optimal ESS charging scenario to improve fuel

economy and ESS lifetime. The engine speed and

torque could be located in the high-efficiency

region. Meanwhile the ESS lifetime extends due to

the designed charging curve avoiding negative

charging status, chaotic and surge currents, or

persistent high power. ADVISOR-based simulation

results validate the proposed powertrain control

system.

REFERENCES

Plsu, P., Rizzoni, G., 2005. A supervisory control strategy

for series hybrid electric vehicles with two energy

storage systems, In IEEE Vehicle Power and

Propulsion Conference.

Wang, Z., Huang, B., Xu, Y. et al., 2008. Optimization of

series hybrid electric vehicle operational parameters

by simulated annealing algorithm, In IEEE

International Conference on Control & Automation.

Kachroo P., Tornizuka, M., 1996. Chattering reduction

and error convergence in the sliding-mode control of a

class of nonlinear systems, IEEE Transactions on

Automatic Control.

Utkin, V. I., Guldner, J., Shi, J., 2009. Sliding mode

control in electro-mechanical systems, CRC Press.

Boca Raton.

Svoboda, V., Wenzl, H., Kaiser, R. et al., 2007. Operating

conditions of batteries in off-grid renewable energy

systems, Solar Energy.

SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems

238