
A CONTROL PARADIGM FOR DECOUPLED OPERATION
OF MOBILE ROBOTS IN REMOTE ENVIRONMENTS
Remo Pillat, Arjun Nagendran and Charles E. Hughes
Synthetic Reality Lab, University of Central Florida, 3100 Technology Pkwy, 32826, Orlando, FL, U.S.A.
Keywords:
Mobile Robots, Tele-operation, Virtual Environments, Robot Simulation.
Abstract:
Remote operation of robots in distant environments presents a significant challenge for direct control due
to inherent issues with latency and available bandwidth. Purely autonomous behaviors in such environments
come with the associated risks of failure. It may be advantageous to acquire information about the environment
from the robot’s onboard sensors, to re-create a simulation and plan a mission beforehand. The planned
mission can then be uploaded to the robot for execution, allowing the physical robot to handle the autonomy
required for completing its task. In this paper, the foundations of a control paradigm are presented that uses
a simulated virtual environment to decouple the operator from the physical robot, thus circumventing latency
problems. To achieve this, it is first required to accurately model the robot’s kinematic parameters for use in
the simulation. Kalman filtering techniques that demonstrate this modeling for a differential drive robot are
presented in this paper. The estimated parameters are then used as inputs to a modular planning and execution
module. Based on simulation results, a safe and non-redundant path can then be uploaded and executed on the
real robot.
1 INTRODUCTION
Robots have become a ubiquitous presence in today’s
society. They have found uses in diverse areas such
as manufacturing, health care, planetary exploration,
and entertainment. Autonomous operation of these
robots is usually limited to processes that occur in
controlled environments and involve repetitive steps,
e.g. the assembly of cars.
Whenever a robot is deployed on a remote mis-
sion, some form of tele-operation has to be employed.
Conventionally, tele-operation refers to the direct con-
trol of a robot from a remote location using onboard
sensors that provide the required navigational aids. In
mobile robotics this need is most pronounced in ex-
ploring areas that are hazardous or inaccessible to hu-
mans, e.g. when surveying a stricken nuclear plant
or controlling a rover on a different planet. Recently,
the medical community has made long strides towards
making minimally invasive robotic surgery a routine
procedure, but in most commercially available sys-
tems the operator has to be located in close physical
proximity. Remote tele-operation is however always
hampered by the inescapable bandwidth limitations
and communication time delays (latency).
Transmission delays and bandwidth limitation are
an unavoidable feature of long-distance communica-
tion. These must be compensated for within existing
control schemes or an alternative control paradigm
must be applied. In this work, an architecture will be
presented that decouples the operator’s actions (mas-
ter) on a simulated robot from the executed actions on
the real robot (slave) through a virtual reality-based
simulation layer. The general control paradigm is
based on the following assumptions that are not pre-
sented in the scope of this paper.
• The simulation environment can be constructed
by gathering real-world data through the robot’s
onboard sensors and is sufficiently representative
within a localized region around the robot.
• The real robot has sufficient autonomy to be able
to execute a mission plan under the influence of
external uncertainties, or report discrepancies that
prevent execution.
An operator can work in the simulation environment
to plan and execute his mission either by controlling
the robot manually, or experiment with higher level
autonomous planning modules. Once mission execu-
tion in simulation is completed, a set of modules pro-
cess the simulation data to re-create a mission plan
for the real robot. The modules are capable of accept-
ing user inputs to prioritize the mission’s goals and
553
Pillat R., Nagendran A. and E. Hughes C. (2012).
A CONTROL PARADIGM FOR DECOUPLED OPERATION OF MOBILE ROBOTS IN REMOTE ENVIRONMENTS.
In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 553-561
DOI: 10.5220/0003947205530561
Copyright
c
SciTePress

remove any redundancy in the simulated mission. A
newly created mission plan is then uploaded to the
real robot for execution. The work presented herein
focuses on the use of Kalman filtering techniques to
determine the robot’s kinematic parameters and the
role of the different modules in the decoupling pro-
cess.
2 BACKGROUND
Traditionally, bilateral tele-operation with time delays
requires specialized control schemes to assure sys-
tem stability and transparency. Good surveys of these
methods can be found in (Arcara and Melchiorri,
2002) and (Hokayem and Spong, 2006).
All of these methods try to address the problem
of direct control of the slave by the master under the
presence of time delay. If the time delays are highly
variable or impractical to the operators other methods
have to employed. (Pan et al., 2006) takes a new ap-
proach be proposing a dual predictor/observer control
schemes on both the master as well as the slave side,
thus circumventing the usage of any delayed informa-
tion.
In one of the earliest attempts for an alternative
paradigm, (Bejczy et al., 1990) displays a virtual
”phantom robot” on the master side that can be con-
trolled directly without time delay. In these experi-
ments the real robot arm follows the phantom move-
ments with the implicit time delay. Unfortunately,
this scheme increases the execution time of any mo-
tion, because the operator will perform a motion on
the phantom robot and then has to wait until the real
robot attains the same configuration. (Kheddar, 2001)
first introduced the ”hidden robot concept” that com-
pletely abstracted the movements of the real robot
from the operator by only presenting him with a vir-
tual presentation.
(Kheddar et al., 2007) provides a more recent sur-
vey of the state-of-the-art in using virtual reality sim-
ulations to overcome the inherent tele-operation lim-
itations. Closely related to our work is the emerg-
ing field of Teleprogramming (Hernando and Gam-
bao, 2007) where the operator does not directly con-
trol the robot, but a simulated copy. After an action is
executed, an abstract command sequence that signals
operator intent is sent to the slave robot. The authors
make an effort to abstract the underlying system vari-
ables on the master and slave side and only transmit
operator intentions. This approach is laudable in its
generalizing power, but has implicit requirements of
accurate simulation models for robots and the envi-
ronment.
With exception of (Wright et al., 2006) and (Yu
et al., 2009), many teleprogramming systems focus
on the operation of robot arms, while systems tailored
towards mobile robot tele-operation have gained less
attention. This might be due to the fact that the phys-
ical simulation of mobile robots dynamics and envi-
ronment interaction is non-trivial.
Professional robot simulators have sufficiently ad-
vanced to provide a satisfactory simulation of physi-
cal interactions between robot and the environment.
Examples of commercial systems include Marilou
(Anykode, 2011), Webots (Michel, 2004), and Mi-
crosoft Robotics Studio (Jackson, 2007).
Predictive simulators have also been used to allow
multi-robot coordinating missions as in (Chong et al.,
2000).
3 SYSTEM ARCHITECTURE
As stated previously, transmission delays, missing
communication packets, and bandwidth limitation are
an unavoidable feature of long-distance communica-
tion. Communication latencies beyond several hun-
dred milliseconds are generally unacceptable for hu-
man operators and produce dangerous control insta-
bilities. This paper proposes an architecture that
decouples the operator’s actions from the executed
motions of the robot. This has several advantages
that can not be achieved in traditional tele-operation.
Given a representation of the environment, operators
can plan and execute simulated missions without the
need for a permanent communication connection to
the physical robot. Time-intensive trial runs can be
shortened, while invalid inputs and redundancies can
be corrected before any commands are uploaded to
the real robot.
The general control infrastructure will support
both goals of visual and operational fidelity on the
master’s side as well as tight closed-loop control with-
out time delay by the slave (Figure 1).
At the highest level, our Master-Slave Control Ar-
chitecture (Zhu et al., 2011) features a simulation
server that maintains an environmental model and
simulated robotic entities with sensors and actuators.
All simulation components are based on the com-
mercial Marilou robotics simulator (Anykode, 2011).
Without a physical complement, a program can be
launched locally that controls the movements of the
robot in the simulated environment. This is the master
layer and it can function independently of any other
communication.
The uniqueness of the control architecture lies
in decoupling the networked layers. The simulation
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
554

Figure 1: General architecture of the control paradigm.
layer is used to plan and execute movements before-
hand. These planned movements guide the real robot
that attempts to closely follow the simulated robot
without the need for explicit user control, while main-
taining a degree of autonomy to cope with dynami-
cally changing situations.
A remote program residing on the slave in the
real world connects to the Master and reads the val-
ues from the simulated sensors / actuators. The com-
munication interface then translates the actuator com-
mands to the real-robot (slave). At the same time,
real world sensors are read and data is fed back to
the simulation establishing a bilateral communication
interface; discrepancy in the received data from that
predicted by the simulation causes control to be trans-
ferred back to the Master.
The strength of the presented system, in compari-
son to the predictive simulation systems mentioned in
section 2, is its inherent ability to initially identify and
continually update the simulated representation of the
robot. Previous work relied heavily on a priori avail-
able simulation models or overly simplified physical
modeling. In addition, the modularity of the archi-
tecture allows easy addition of high-level planning or
processing modules.
While interpreting sensor data to recreate a simu-
lation dynamically forms one component, it is equally
important to have a robust model of the robot itself
in the simulation. Section 4 will focus on the use
of Kalman filtering techniques to estimate the robot’s
kinematic parameters for use in simulation. These es-
timates are then passed as inputs to the modular plan-
ning and execution system which processes the simu-
lated data to generate a feasible mission plan for the
real robot (see Section 5). The significance of estima-
tion errors in these parameters on the simulation are
highlighted in Section 6.
4 KINEMATIC ROBOT
SIMULATION MODEL
An accurate kinematic model of the controlled entity
is essential for any predictive simulation of robot mo-
tions. The existence and accuracy of this model is an a
priori requirement for both the validity of the physical
simulation in the master virtual environment as well
as the legitimacy of any simulated planning action.
In existing systems that demonstrated the tele-
operation of mobile robots, for example (Yu et al.,
2009) and (Wright et al., 2006), this robot model is as-
sumed to be provided to the simulator with sufficient
accuracy. In most cases, the parameters of this model
are hard to quantify, because values from manufac-
turer’s specifications or manual measurements are ei-
ther non-existent, prone to errors, or can vary from
one robot to the next. Through the example in Sec-
tion 6 it will be convincingly argued that even small
changes of the robot’s kinematic variables have a str-
A CONTROL PARADIGM FOR DECOUPLED OPERATION OF MOBILE ROBOTS IN REMOTE ENVIRONMENTS
555

ong influence on the accuracy of the motion simula-
tion in the planning and execution stages. For any
system employing a simulated mobile robot, this fact
cannot be overstated, because in the overall system ar-
chitecture many higher level modules will depend on
the precision of the kinematic parameters.
This makes the need for an automatic calibra-
tion method more pronounced. In this section, the
kinematic model of the well-known differential drive
configuration will be developed. In addition, a uni-
fied framework for the automatic identification of the
kinematic parameters of a differential-drive robot will
be presented that allows off-line as well as online es-
timation. Ideally, this process will be self-calibrating
and should not require any human control input be-
yond a rough initial value of the estimated entities.
4.1 Basic Differential Drive Model
The differential drive configuration is a commonly en-
countered mobile robot combination that uses two ac-
tuated wheels and one or more (passive) casters. For
the purposes of this work the parameters of this con-
figuration can be simplified according to Figure 2.
The kinematic parameters that should be esti-
mated are the diameters of the left and right wheels
(d
L
and d
R
, respectively), and the wheel base b.
Figure 2: Differential drive configuration. Here d
L
and d
R
denote the diameters of the left and right wheel, respec-
tively. c is the center point between the actuated wheels
and b is the wheelbase.
When the robot moves in 2D its basic state at time
instant k can be described by x = [x,y, θ]
T
. Here the
coordinates (x,y) denote its position and θ the orien-
tation of its body.
Depending on the sampling time, the movement of
a differential drive robot can be approximated either
by a linear motion or, more generally, a circular arc.
Following the derivation for the latter case outlined in
(Wang, 1988), the state transition between time steps
k and k + 1 can be described as follows:
x =
x
k−1
y
k−1
θ
k−1
+
sin(α)
α
∆s cos(θ
k−1
+ α)
sin(α)
α
∆s sin(θ
k−1
+ α)
∆θ
k
(1)
Here ∆s denotes the distance that the center c of
the robot traverses along the circular arc. The change
in orientation is signified by ∆θ
k
. α = ∆θ
k
/2 is simply
the half angle of the orientation change.
4.2 Incorporating Odometry Readings
In most cases, the odometry of the robot is derived
from encoders that are mounted on the driveshaft of
the actuated wheels. Even if they are not equipped on
a mobile base, they can easily be retrofitted.
Let e
res
be the encoder resolution per wheel rota-
tion. This value is constant and assumed to be known.
The encoder count differences between time steps are
indicated by ∆e
L
for the left wheel and ∆e
R
for the
right one.
Then the values for ∆s and ∆θ in Equation (1) can
be reformulated (under no wheel-slip conditions) as:
∆s =
∆s
R
+ ∆s
L
2
=
π (d
L
∆e
L
+ d
R
∆e
R
)
2 e
res
(2)
∆θ =
∆s
L
− ∆s
R
b
=
π (d
L
∆e
L
− d
R
∆e
R
)
e
res
b
(3)
∆s
L
is the distance traveled by the left wheel and
∆s
R
the equivalent quantity for the right wheel.
These derived equations will be used for estimat-
ing the state of the robot between time steps. Because
the robot state depends on our kinematic unknowns,
they can be estimated continuously while the robot
drives an arbitrary path.
4.3 Online Estimation
For estimating the state of a linear system, the Kalman
Filter (Kalman, 1960) and its many derivatives have
been the de facto standard in the robotics commu-
nity. Under the assumption that all state variables are
perturbed by zero-mean normal-distributed noise, the
Kalman Filter is an optimal recursive estimator for the
state variables of linear dynamical systems.
As can readily be seen by inspecting Equation (1),
the state transition between samples is described by
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
556

nonlinear equations. To handle that, this paper will
use the Extended Kalman Filter (Julier and Uhlmann,
2004), which linearizes the state transition equations
around the current mean and covariances of the esti-
mated quantities.
Akin to the state description in Section 4.1, our
state vector is x, but the process is now governed by
the non-linear function f :
x
k
= f (x
k−1
,w
k
) (4)
Here, the non-linear function f relates the state
x
k−1
from the last time step and process noise w
k
∼
N(0,Q) to the current state.
A vector of measurements can be calculated by:
z
k
= h(x
k
,v
k
) (5)
Here, the non-linear function h relates the a priori
state x
k
and measurement noise v
k
∼ N(0, R) to the
expected measurements z
k
.
In the update step of the filter, external measure-
ments of the robot state need to be integrated into the
current estimate. For the purposes of the experiments
presented here, the absolute position and orientation
of the robot is measured through an external optical
tracking system by Optitrack. Alternatively, a scan
matching based approach with a mounted laser scan-
ner could be used.
4.4 Augmented Extended Kalman Filter
The state vector x = [x,y,θ]
T
can be used to estimate
the pose of the robot based on internal encoder and
external tracking readings as outlined in Section 4.3.
If the values of the wheel diameters d
L
and d
R
and
the wheel base b are known only approximately or
are variable during robot operation, systematic errors
will be injected into the estimation process. This will
invariably lead to a degradation of Kalman Filter per-
formance. Examples of systematic errors include un-
equal wheel diameters, wheel misalignment, and ef-
fective wheel base ambiguities due to non-point floor
contact.
To alleviate that, the ideas from (Larsen, 1998)
and (Martinelli et al., 2007) can be followed to aug-
ment the state vector by the unknown quantities. De-
viating from this previous work, the wheel diameters
and wheel base are added directly to the state vec-
tor instead of using an artificial multiplier. The aug-
mented state vector is thus
x = [x,y,θ,d
L
,d
R
,b]
T
(6)
The linearized (6x6) system matrix can be derived
based on the Jacobians of the non-linear function f in
Equation (4). The partial derivatives can be readily
found through symbolic differentiation in Matlab.
4.5 Experimental Validation
To validate the usefulness of the filter proposed in
Section 4.4, the robot is driven multiple times along a
circular path with a set of predetermined wheel veloc-
ities. Encoder readings of both wheels are recorded at
20 ms intervals.
The absolute position and orientation of the robot
is determined by a mounted marker pattern that is
tracked by an infrared camera system. The optical
tracking data was logged and served as ground truth
for this test run.
The test is performed at relatively slow speeds, so
wheel slippage on the surface can be ignored. After
the run concludes, the Augmented EKF is executed
off-line on the log data. For the purposes of this evalu-
ation, only the mean estimated values for wheel diam-
eters d
L
and d
R
and wheel base b are used for further
calculations.
As a baseline, d
L
, d
R
, and b were measured man-
ually and the robot path was calculated through the
dead reckoning equations ( Equation (1) and Equa-
tion (2)). One would expect the shape of the resulting
circle to closely resemble the shape recorded by the
optical tracker.
To each set of circles, an ellipse was fitted and
its measurements for major axis, minor axis and area
were used as indicators for the validity of the esti-
mated parameters. Table 1 shows the results of this
run.
Table 1: The robot is driven along a circular path. Tracking
data is collected and a dead-reckoned path is calculated for
different values of wheel diameters and wheel base. The
”Baseline” is measured manually (d
L
= d
R
= 6.44 cm, b =
26 cm), while the ”Calibration” values are the mean output
of the Augmented Extended Kalman Filter (d
L
= 4.647 cm,
d
R
= 4.517 cm, b = 26.98 cm).
Major Axis a Minor Axis b Ellipse Area
(in cm) (in cm) (in cm
2
)
Tracking Data 107.714 107.44 9089.235
(Ground Truth)
Dead Reckoning 109.875 109.036 9409.337
(Baseline)
Dead Reckoning 107.101 106.387 8948.930
(Calibration)
Clearly, the quality of the dead reckoning im-
proves with the newly calibrated values. This bodes
well for the integration of the calibration into the vir-
tual reality simulation of the mobile robot.
Although this experiment was performed off-line
for convenience, the Kalman filter is designed to ex-
ecute online while the robot is running and continu-
ously update its estimates.
A CONTROL PARADIGM FOR DECOUPLED OPERATION OF MOBILE ROBOTS IN REMOTE ENVIRONMENTS
557
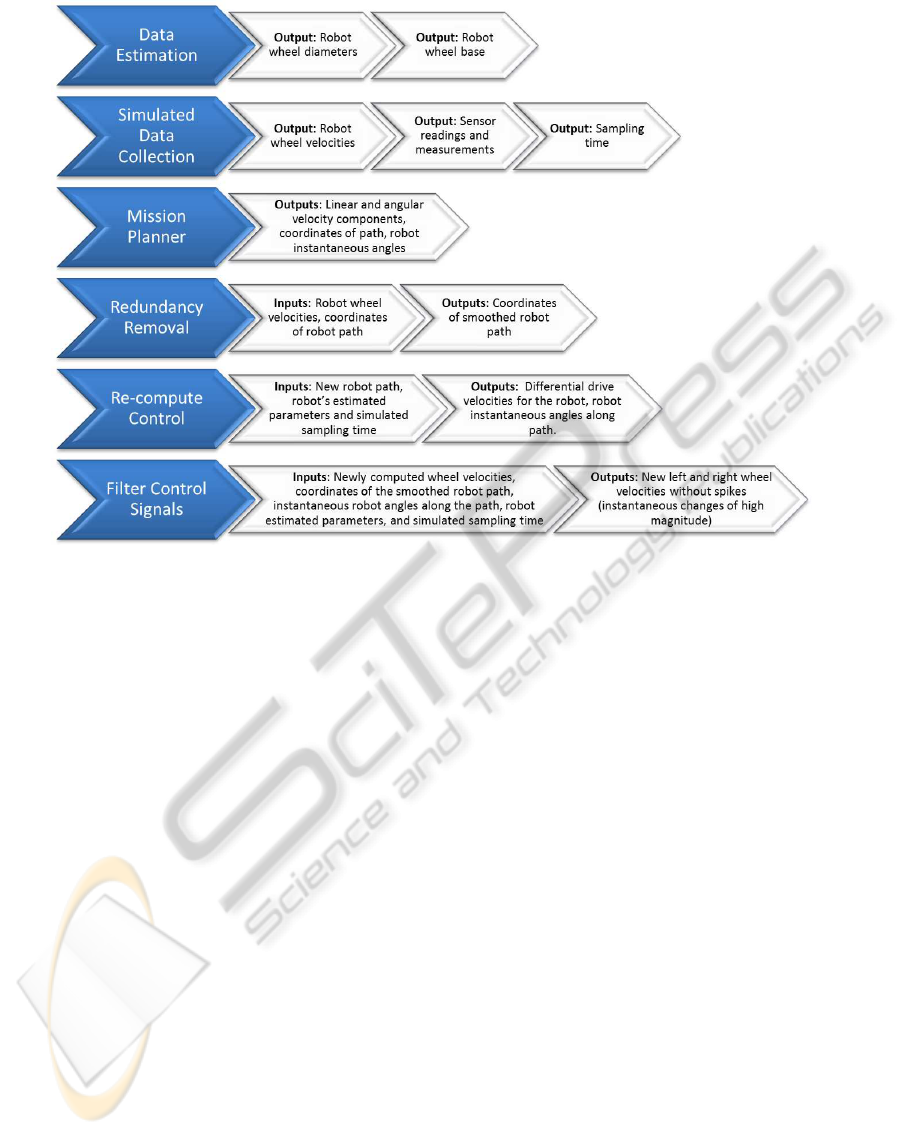
Figure 3: Planning and execution modules.
5 PLANNING AND EXECUTION
IN SIMULATION
The planning and execution stage is used on the mas-
ter (simulation) side of the tele-operation to allow the
operator to explore planning strategies and preview
anticipated robot movements. This stage is divided
into modules that are processed sequentially until a
final successful behavior can be implemented on the
real robot. Figure 3 depicts the six modules used
during planning and execution, highlighting the in-
puts and outputs of each module. The absence of an
explicit input indicates that this information directly
flows in from the outputs of the module above it.
Data Estimation: The data estimation module is
implemented according to the description in Section 4
i.e. the robot wheel diameters and wheel base are es-
timated using a Kalman Filter.
Simulated Data Collection: The data collection
module logs all simulated data during a mission, in-
cluding sampling time, left and right wheel velocities
of the robot, encoder counts, and all readings of the
mounted sensors.
Mission Planner: The mission planner integrates
the estimated and simulated data to re-create the exe-
cuted mission including generation of the coordinates
of the robot path that must be passed as an input to the
redundancy removal module.
Redundancy Removal: This module initializes
regions of interest based on the definition of redun-
dancy (user-specified). A matrix of distances between
the coordinates on the redundant path is used to find
pinch points (intersecting points) across the curves.
These pinch points are used to delete any kinks or
loops in the robot path, which are redundant.
Re-compute Control: The new path (time-series)
is used to regenerate velocity vectors for the robot i.e.
individual wheel velocities for the differential drive
steering mechanism are re-computed based on the de-
sired linear and angular velocities.
Filter Control Signals: The deletion of segments
in the original path may result in the new path requir-
ing instantaneous changes in robot velocity, leading to
spikes in the control signal for each wheel. As a result
of this deletion, the robot might be expected to be in a
new position at the next sampling instant that is phys-
ically infeasible to attain. The path must therefore
be re-interpolated between the regions where spikes
occur, resulting in smoothed control signals for each
robot wheel. For every control signal spike, the path
of the robot is interpolated by increasing the travel-
time between the spike-points. This involves a re-
sampling of the position and velocity vectors of the
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
558
robot to increase overall time for the mission. The
orientation of the robot must be interpolated sepa-
rately since simultaneous changes in position and ori-
entation of the robot can occur during the removal
of kinks. Magnitude of velocity and angular veloc-
ity of robot are together used to determine left and
right wheel velocities. The process is also iterative
for each spike in the list, since the newly computed
values for position and orientation are re-used in the
interpolation process.
5.1 Case Study: Simple Wall Following
Routine
A simulation scenario was created with a right-angled
wall in the center of an indoor environment as shown
in Figure 4. The simulated robot had a single infrared
sensor mounted at its side at an acute angle, and a
bump sensor. The robot utilized a differential drive
steering and was programmed to perform a simple
wall following routine. When the bump sensor was
triggered on contact, it would cause the robot to re-
verse; following which it turned to its left and moved
along the wall using a loosely tuned proportional con-
troller acting on the error from the desired wall dis-
tance. The green dotted lines in the depiction indi-
cate a rough path that the robot would follow when
this algorithm was used. The red dots indicate regions
where the robot would have to back up since the bump
sensor was triggered.
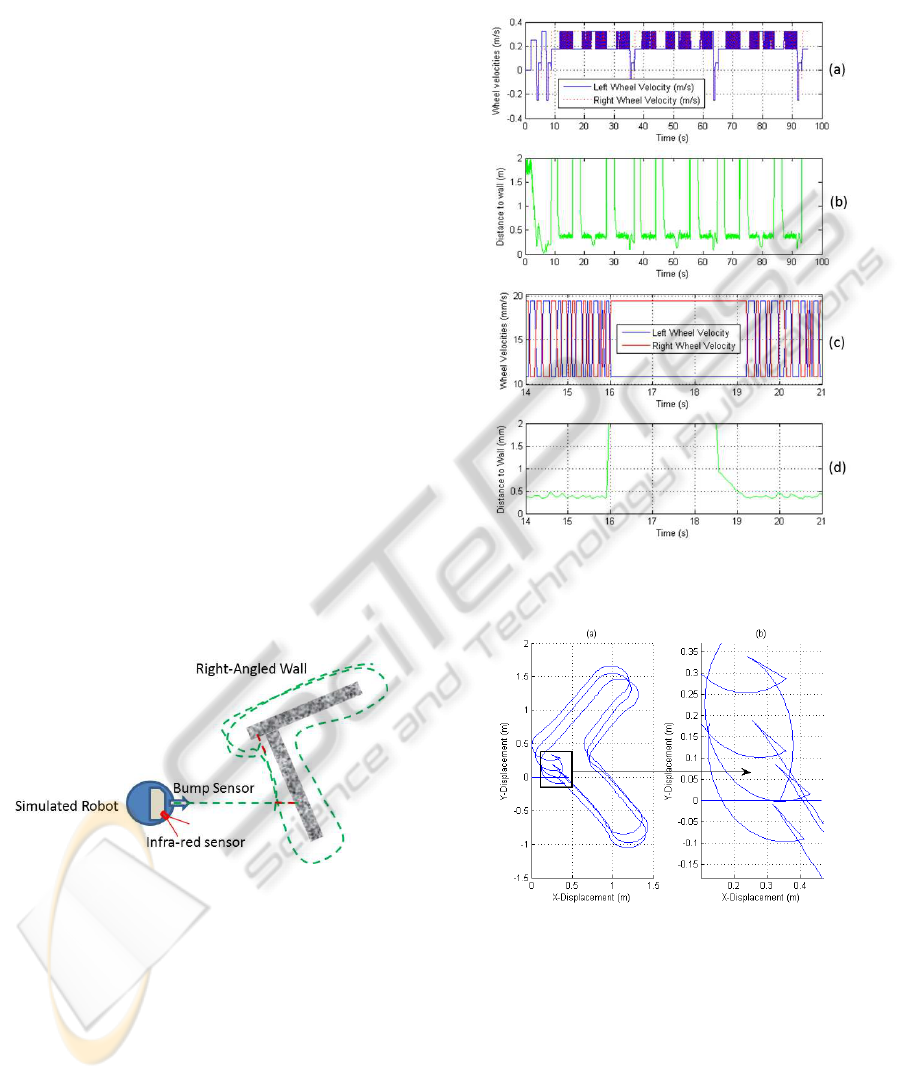
Figure 4: Simulation setup.
Figure 5(a) shows the left and right wheel veloc-
ities during the wall following routine. Figure 5 (b)
shows the distance to the wall as measured by the
on-board infrared sensor. A section of both graphs
is magnified for closer examination (Figure 5(c) and
Figure 5(d)). The data is generated by combining the
data estimation and simulated data collection mod-
ules. The continuous oscillations to compensate for
the wall distance-error highlights the implementation
of the proportional controller. Notice that the high
values of wall distance result in a corresponding dif-
ference in wheel velocities causing the robot to turn
in an arc until the infrared sensor picks up the wall
again.
Figure 5: Wall distance and wheel velocities. The graphs
are described in detail in Section 5.1.
Figure 6: Path of robot during wall-following.
Figure 6 (a) shows the actual path of the robot
around the right-angled wall in the simulation. This
is generated by the mission planner module. A por-
tion of Figure 6 (a) has been zoomed into in Figure 6
(b) to show the redundant traversal of paths by the
simulated robot. This occurs when the bump sensor
makes contact with the wall and the robot backs up
before turning away. In this case, redundancy is de-
fined as a portion of the path that can be eliminated
from the simulated path, without causing a change
A CONTROL PARADIGM FOR DECOUPLED OPERATION OF MOBILE ROBOTS IN REMOTE ENVIRONMENTS
559

Figure 7: Regions of interest showing ’pinch points’.
to the robot’s exploration route that would result in
the oversight of valuable information. All sections of
’bump and backup’ are therefore classified as redun-
dant.
Figure 7 shows the regions of interest identified
based on the mission planner and the correspondingly
computed pinch points. These pinch points are pro-
cessed to delete redundant segments of the path in be-
tween. This task is performed by the redundancy re-
moval module, resulting in a smooth path as shown
in Figure 8 (a). The smooth path is passed as an
input to the re-compute control module which cal-
culates the wheel velocities required to achieve the
new path. The module also notifies the filter control
signal module of any instantaneous large changes re-
quired in the wheel velocities to help the robot achieve
a specific position and orientation. These are shown
in Figure 8(a). The filter control signal module then
interpolates the path as described previously to help
achieve a final smoothed path for upload to the main
robot. The processed control signals (before and after
removal of spikes) for each of the wheel modules is
shown in Figure 9. It must be noted that in the newly
calculated path (for upload to the real robot), there
are no collisions with the wall, since this has already
been compensated for from the information provided
by the simulation.
6 EFFECT OF ERRORS IN
PARAMETER ESTIMATION
The mission planning module relies on the estimated
kinematic parameters to determine the robot’s path
in simulation. Specifically, the module integrates the
wheel velocities over time to determine the path taken
by the robot during the simulated mission. Errors
in the kinematics therefore propagate through all the
modules from an early stage. To illustrate this effect,
Figure 8: (a) Output from the re-compute control module
indicating control signal spikes. (b) Filtered path after re-
moval of control signal spikes by the final module.
Figure 9: Control signal (wheel velocities) for the left and
right wheels of the robot.
the estimated wheel base value was modified by 4%
on either side of the ideal value. The drift in the sim-
ulated path on either side of the actual path as shown
in Figure 10 is a result of this error in the estimate.
The mean squared errors between the actual path and
the resultant error-ridden paths (±4%) are found to be
0.1043 m and 0.1033 m respectively, while the sums
of absolute difference between the paths are found to
be 198.6847 m and 196.7018 m correspondingly.
7 CONCLUSIONS AND FUTURE
WORK
This paper presented a decoupled control paradigm
for the tele-operation of mobile robots. The proposed
control architecture benefits applications that have
to deal with intermittent communication channels or
varying time delays. A general system architecture
has been described that integrates a virtual reality-
based physical simulation and lends itself to rapid
mission planning, modular development and distribu-
GRAPP 2012 - International Conference on Computer Graphics Theory and Applications
560
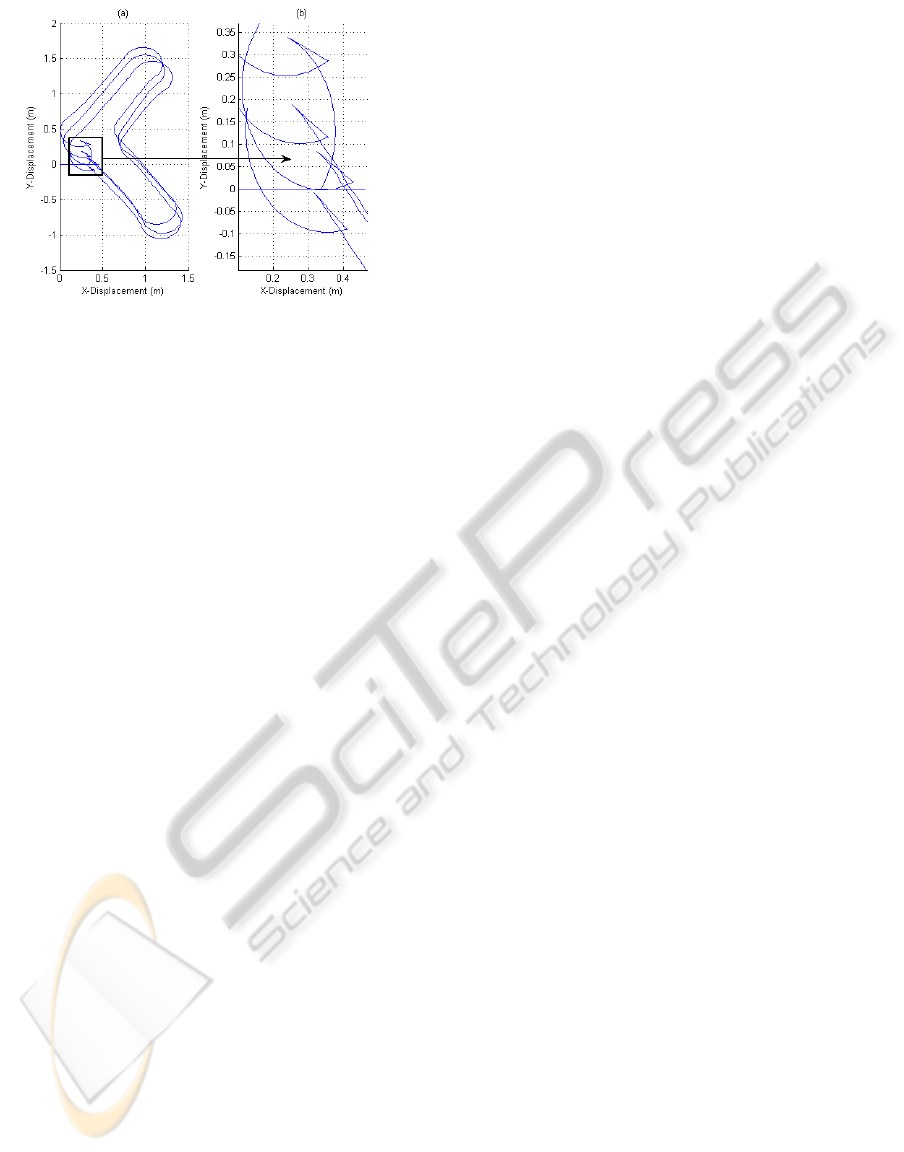
Figure 10: Effect of wrongly estimated wheel base.
tion across a network. Preliminary experimental re-
sults on a sub-section of the control paradigm have
been shown that demonstrate how kinematic parame-
ters of a robot can be estimated and used to improve
simulation results. In addition, an exemplar of a plan-
ning and execution module was described to empha-
size the advantages of the presented system in com-
parison to traditional direct control paradigms.
Since the Augmented Extended Kalman Filter
framework is in place, it can be integrated on the
physical robot to continuously provide an updated
robot state estimate. The presented framework can
accommodate any numbers of sensor inputs, but fus-
ing data from heterogeneous sources is a non-trivial
problem and needs to be investigated. In particular,
how the chosen robot path influences the evolution
and error covariances of the estimates for the robot’s
kinematic parameters should be investigated.
In addition, the components of the system that
have not been treated here, like environment model-
ing, slave-robot command execution and control need
to be examined and integrated.
REFERENCES
Anykode (2011). anyKode Marilou - Modeling and Simu-
lation Environment for Robotics; Last accessed 2 Jan-
uary 2012.
Arcara, P. and Melchiorri, C. (2002). Control schemes for
teleoperation with time delay : A comparative study.
Robotics and Autonomous Systems, 38:49–64.
Bejczy, A., Kim, W., and Venema, S. (1990). The phantom
robot: predictive displays for teleoperation with time
delay. In Proceedings, IEEE International Conference
on Robotics and Automation, pages 546–551. IEEE
Comput. Soc. Press.
Chong, N. Y., Kotokul, T., Ohba, K., Komoriya, K., Tanie,
K., and Mechanics, E. (2000). Use of Coordinated
On-line Graphics Simulator in Collaborative Multi-
robot Teleoperation with Time Delay. In Proc. IEEE
International Workshop on Robot and Human Inter-
active Communication, pages 167–172, Osaka, Japan.
Hernando, M. and Gambao, E. (2007). Teleprograming:
Capturing the Intention of the Human Operator. In Ad-
vances in Telerobotics, volume 31 of Springer Tracts
in Advanced Robotics, chapter 18, pages 303–320.
Springer.
Hokayem, P. and Spong, M. (2006). Bilateral teleoperation:
An historical survey. Automatica, 42(12):2035–2057.
Jackson, J. (2007). Microsoft robotics studio: A techni-
cal introduction. Robotics & Automation Magazine,
IEEE, 14(4):82–87.
Julier, S. and Uhlmann, J. (2004). Unscented filtering
and nonlinear estimation. Proceedings of the IEEE,
92(3):401–422.
Kalman, R. E. (1960). A New Approach to Linear Filtering
and Prediction Problems. Journal of Basic Engineer-
ing, 82(Series D):35–45.
Kheddar, A. (2001). Teleoperation based on the hidden
robot concept. Systems, Man and Cybernetics, Part A:
Systems and Humans, IEEE Transactions on, 31(1):1–
13.
Kheddar, A., Neo, E., Tadakuma, R., and Yokoi, K.
(2007). Enhanced Teleoperation Through Virtual Re-
ality Techniques. In Ferre, M., Buss, M., Aracil, R.,
Melchiorri, C., and Balaguer, C., editors, Advances
in Telerobotics, volume 31 of Springer Tracts in Ad-
vanced Robotics, chapter 9, pages 139–159. Springer.
Larsen, T. (1998). Optimal Fusion of Sensors. Phd thesis,
Technical University of Denmark.
Martinelli, A., Tomatis, N., and Siegwart, R. (2007). Simul-
taneous localization and odometry self calibration for
mobile robot. Autonomous Robots, 22(1):75–85.
Michel, O. (2004). Webots TM : Professional Mobile
Robot Simulation. International Journal of Advanced
Robotic Systems, 1(1):39–42.
Pan, Y.-j., Canudas-de wit, C., and Sename, O. (2006).
A New Predictive Approach for Bilateral Teleoper-
ation With Applications to Drive-by-Wire Systems.
Robotics, IEEE Transactions on, 22(6):1146–1162.
Wang, C. (1988). Location estimation and uncertainty anal-
ysis for mobile robots. In Proceedings. 1988 IEEE In-
ternational Conference on Robotics and Automation,
pages 1231–1235. IEEE Comput. Soc. Press.
Wright, B. Y. J., Hartman, F., Cooper, B., Maxwell, S.,
Yen, J., and Morrison, J. (2006). Driving on Mars
with RSVP - Building Safe and Effective Command
Sequences. Robotics & Automation Magazine, IEEE,
13(2):37 – 45.
Yu, C.-q., Ju, H.-h., Gao, Y., and Cui, P.-y. (2009). A
Bilateral Teleoperation System for Planetary Rovers.
In 2009 International Conference on Computational
Intelligence and Software Engineering, pages 1–5.
IEEE.
Zhu, J., He, X., and Gueaieb, W. (2011). Trends in
the Control Schemes for Bilateral Teleoperation with
Time Delay. Autonomous and Intelligent Systems,
6752:146–155.
A CONTROL PARADIGM FOR DECOUPLED OPERATION OF MOBILE ROBOTS IN REMOTE ENVIRONMENTS
561
