A NEW

VISUALIZATION METAPHOR

FOR ASSOCIATION

RULES

Zohra Ben Said

, Fabrice Guillet

, Paul Richard

, Julien Blanchard

and Fabien Picarougne

LINA, UMR 6241 CNRS, University of Nantes, Nantes, France

LISA, EA 4094, University of Angers, Angers, France

Keywords: Visual Data Mining, Visualization, Knowledge Discovery in Database, Association Rules.

Abstract: In order to discover knowledge from large amount of results generated by the association rules extraction

algorithms, visual representations of association rules can be very beneficial to the user. Those

representations support the user in finding and validating interesting knowledge. All techniques proposed

for association rule visualization have been developed to represent association rule as a hole without paying

attention to the relations between attributes and the contribution of each one. In this article, we propose a

new visualization metaphor for association rules. This new metaphor represents attributes which make up the

antecedent and the consequent, the contribution of each one to the rule, and the correlations between each

pair of antecedent and consequent.

INTR

ODUCTION

Association rule extraction (Agrawal et al., 1993) is

the task of finding correlations between items in a

dataset. Initial research was largely motivated by the

analysis of market basket data, the results of which

allowed companies to more fully understand purcha-

sing behavior and, as a result, better target market

audiences. An association rule is an implication of

the form X

➜ Y, where X (antecedent) and Y

(consequent) are non-intersecting sets of items. For

example, milk, eggs

➜ bread is an association rule

says that when milk and eggs are purchased, bread is

likely to be purchased as well. At the output of the

association rules extraction process, the user

(decision- maker) must evaluate and select the

interesting part of the results (known as rule post-

processing). To select interesting rules from the set

of all possible rules, constraints on interestingness

measures can be used. The best known constraints

are the minimum thresh- olds on support and

confidence.

•

The support:supp(X ➜ Y) = Nb of

transactions which contain X and Y / Nb of

transactions in the database,

•

The confidence:conf

➜

Y) = Nb of

transactions which contain X and Y / Nb of

transactions which contain X.

The main drawback of the association rule

extraction process is the volume of generated rules

which often greatly exceed the size of the

underlying database. Cognitive processing of

thousands of rules takes much more time than

generating them even by a less efficient tool. To

reduce the cognitive load, visual representations of

association rules are used to facilitate and speed up

comprehension and make easier the rules

comparison. All techniques proposed for rule

visualization have been developed to represent an

association rule as a hole without paying attention

to the relations between attributes which make up

the antecedent and the consequent and the

contribution of each one of them to the rule.

Attributes component of an association rule may be

more informative than the rule itself (Freitas, 1998).

Two rules with the same value of interestingness

measures can have very different degrees of

interestingness for the user, depending on which

attributes occur in the antecedent and in the

consequent. In the same way, the information found

in form of relations between the attributes

(correlation) provides the analyst with a better and

clearer image than analysis a rule (Imielinski and

Virmani, 1998). Exploring an association rule

attributes enable deeper insight into the data.

Analysts can be interested by those relationships,

rather than static rule. In this paper we propose a new

803

Ben Said Z., Guillet F., Richard P., Blanchard J. and Picarougne F..

A NEW VISUALIZATION METAPHOR FOR ASSOCIATION RULES.

DOI: 10.5220/0003949308030808

In Proceedings of the International Conference on Computer Graphics Theory and Applications (IVAPP-2012), pages 803-808

ISBN: 978-989-8565-02-0

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

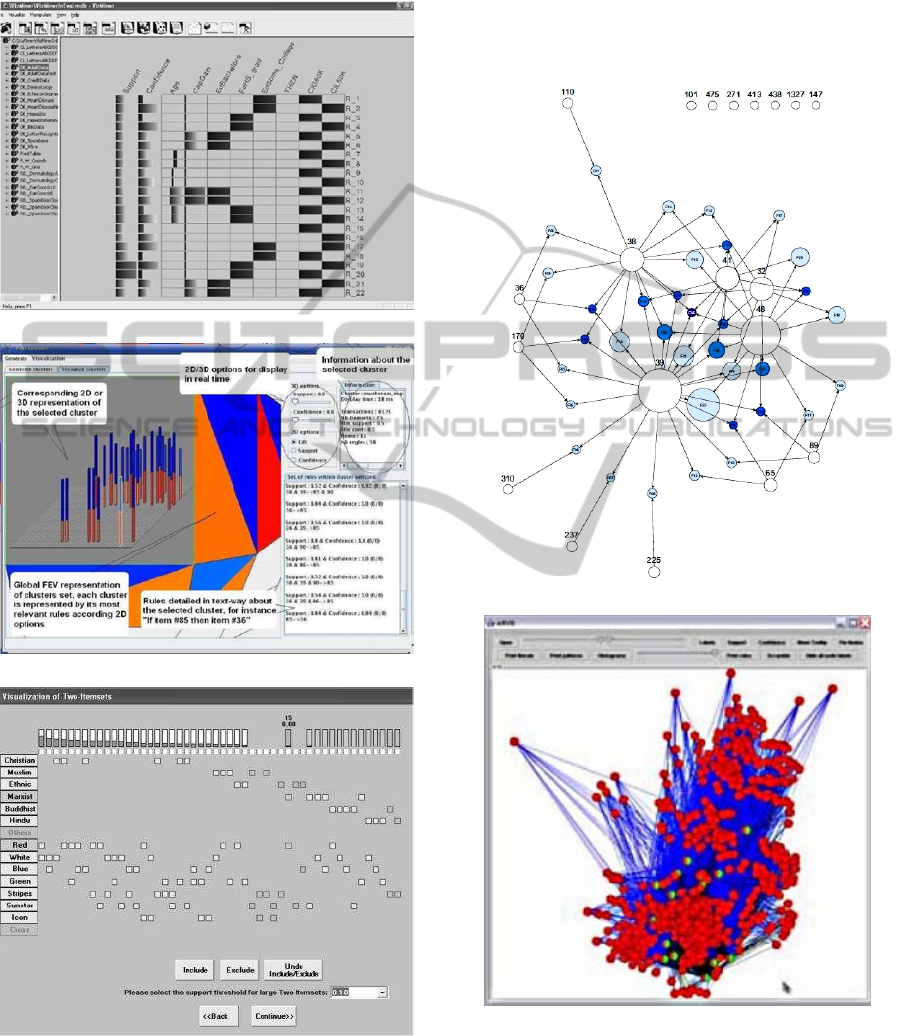
association rule metaphor which represents relations

between at- tributes and the contribution of each one

to the association rule.

(a): (Kopanakis and Theodoulidis,

2003)

(b): (Couturier et al.,

2007)

(c): (Liu and Salvendy,

2006)

Figure 1: Illustrations of association rule visualization tools

based on grid structures and bar charts.

2 ASSOCIATION

ULE

VISU

ALIZ

TION

Visualization can be very beneficial to association

rule mining (Simoff et al., 2008). In fact,

visualization techniques are an effective means to

(d): (Gordal and Demiriz,

2006)

(e): (Bruzzese and Buono,

2004)

Figure 2: Illustrations of association rule visualization tools

based on graph representations.

provide user with meaningful visual

representations

instead of poorly intelligible textual lists. To display

association rules mining results, typical visual

IVAPP 2012 - International Conference on Information Visualization Theory and Applications

804

representations are grid-like structures and bar charts

(Figure.1). The grid view consists of a 2D or 3D

matrix of cells where each cell represents a rule

(Kopanakis and Theodoulidis, 2003; Couturier et al.,

2007; Liu and Salvendy, 2006). One matrix

dimension represents rules antecedents and the other

one represents rules consequent. Each cell is filled

with colored bars indicating rule support and

confidence values. However, this representation

often suffers from occlusion. Moreover, it is difficult

to represent rules if there are too many different at-

tributes in the data or if the rules have many items.

Other visualization techniques are based on graph

visualization (Bruzzese and Buono, 2004; ?), the

nodes and the edges respectively representing the

items and the rules (Figures 2). The interestingness

measures are symbolized by colors and sizes. Other

work uses 3D objects to represent association rule.

In (Blanchard et al., 2007), each rule is represented

by a sphere, whose radius maps its support, and by

a cone, whose base width maps its confidence

(Figure 3). Additionally, the colors of the sphere and

cone redundantly represent a weighted average of the

measures. the rule position in the arena represents the

implication intensity. It’s must be noticed that the

presented methods and techniques are generally

supplied with few interestingness measures and

none of these methods represents the relations

between attributes in the rule and the contribution of

each one of them.

3 IMPORTANCE OF

RULE’S

INDIVIDUAL

TTRIB

UTES

3.1

Attribute Interaction

Two attributes are correlated if they are not

independent. Two attributes are independent if

changing the value of one does not affect the value

of the other. The lift measure calculates the

correlation between two attributes from the

antecedent or the con- sequent. The correlation

between two attributes rep- resents the amount of

information shared among the two attributes. The

lift measure determines whether attribute1 and

attribute2 have a positive (lift >1) or a negative (lift

<1) correlation. The correlation is considered

positive (negative) if the observed frequency of

example satisfying both attribute1 and attribute2 is

greater (smaller) than the expected frequency

assuming statistical independence

between attribute1

and at- tribute2. The (Freitas, 2001) study showed

that the concept of attributes interaction can be

beneficial to the association rule extraction process

and proposed to introduce attribute interaction in the

design of association rule mining systems.

Attributes interaction allows detection surprising

knowledge which can’t be discovered analyzing the

whole rule. The relationships expressed in a rule

totality is quite different from the relationships

expressed in separate rule parts (antecedent and

consequent).

On the other hand, to discover useful association

rules, the user needs to get insight into the data and

understand the relationships between the attributes

and their statistical properties (Chanda et al., 2010).

Exploring attributes relation enables deeper insight

into the data and learn about the data model. In

many case (biological or genetic context for example)

antecedent items has weak associations with

consequent. However, they interact together in a

complicated way to control the consequent

(Chanda et al., 2010).

3.2

Attribute Importance

An attribute can be important for the user if

regularities are observed in a smaller dataset, while

being unobservable in the entire data. A rule can be

considered as disjunction of rules. The size of a

disjunct (rule) is the number of items composed the

rule’s antecedent and the rule’s consequent. For

example: r : X1 X2 X3

➜ Y1 Y2 is a rule. A

disjunction of rules is r1 :

➜

Y1 Y2, r2 :

➜

Y1 Y2, r3 : X3 ➜ Y1 Y2, r4 : Y1 ➜ X1 X2 X3 and

r5 : Y2

➜ X1 X2 X3. At first sight, it seems that this

small rules has no importance, since they can be

considered as a redundant rules. Based on this view,

all most extraction algorithms do not keep this rules

in the results. However, small rules have the

potential to show unexpected relationships in the

data (Freitas, 1998). (Provost and Aronis, 1996)

proved that small rules were considered interesting in

their field application. Accordingly, it would

beneficial that the user can see automatically this

small rules.

In order to evaluate the contribution of each item

to rule (Freitas, 1998) has proposed the Information

Gain measure which can be positive or negative. Item

with high positive Information Gain is considered as

a good one. Item with high negative Information Gain

is considered as a bad one and should be removed

from the association rule. From a rule interesting

perspective, the user knows already the most

important attributes for its field, and rules containing

these items may not be much interesting. At the

same time, a rule includes attributes with low or

A NEW VISUALIZATION METAPHOR FOR ASSOCIATION RULES

805

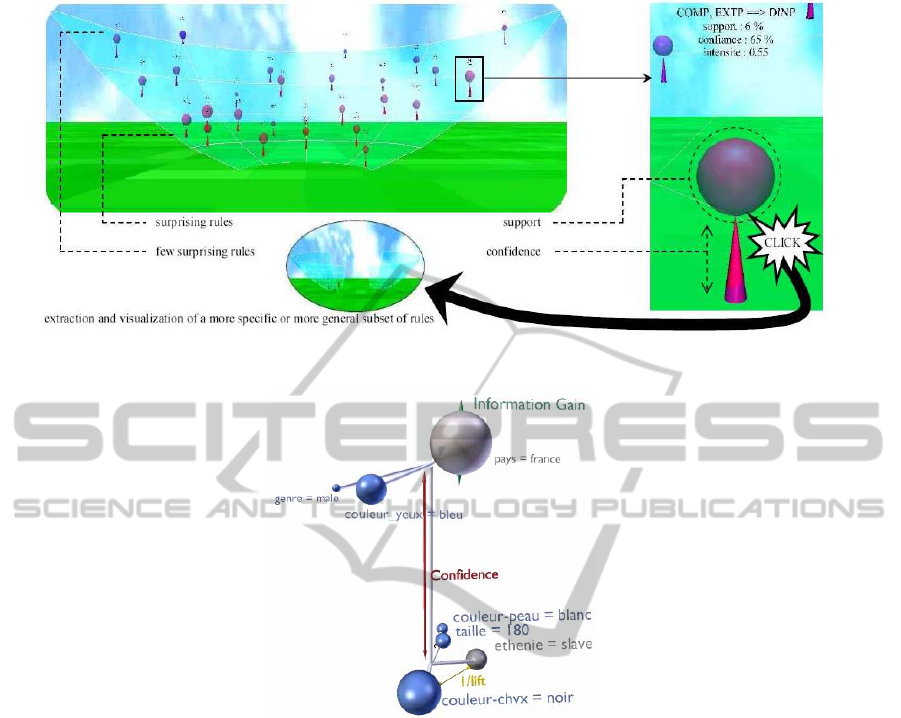
Figure 3: Illustrations of Arvis (Blanchard et al., 2007).

Figure 4: The visual association rule metaphor.

negative information gain (logically irrelevant) can

surprise the user in cases where attributes correlation

can make irrelevant item into a relevant one. This

phenomenon can be interesting to the user.

4 ASSOCIATION RULE

METAPHOR

A major default of association rule visualization

methods presented in Section 2 is the inability to show

the attributes that make up the association rule while

they are may be interesting to the user. Another limit,

some of those methods do not enhance rules

interestingness measures values. For instance,

association rules visualization methods based on

graph or matrix use color to represent some

interestingness measures. This graphic encoding

choice for quantitative variables is known to be

wrong in information visualization (Bertin, 1984).

For our association rule metaphor we refer to

Bertin’s semiology (Bertin, 1984) to encode rule

interestingness measures. As advocated by (Bertin,

1984), we choose a graphic en- coding based on

positions and sizes to enhance the most important

interestingness

measures which is: Information Gain

and correlation between attributes. To have the

greatest degree of freedom we choose to use a 3D

representation. Our metaphor (Figure 4) shows two

types of interestingness measures.

The first one matches rule attributes description

which are categorical variables from the graphic

semiology point of view. Each attribute has an

associated continuous variable corresponding to the

informative gain of each attribute. In the 3D space,

each attribute is represented by a sphere and his size

is an effective representation of this metric. We note

here that the user must know if an item belongs to

the antecedent or the consequent. Therefor, we

should separate the items of the antecedent to the

items of the consequent. in the representation space.

IVAPP 2012 - International Conference on Information Visualization Theory and Applications

806

Figure 5: Illustration of a set of association rules.

The lift is a positive measure which used to

indication how much two items are correlate. A

distance between each two items of the same group

is an effective representation of this metric. More

the items are correlate more the spheres are close. To

generate items coordinates in 3D space we use

dynamic graph (Hendley et al., 1999). The dynamic

graph algorithm enables the spheres self-

organization in the visualization area by the use of a

force system in order to find a steady state and

determine the sphere positions. Using the hyper

system allows correlated items to be near each

other, and independent items to be far away. This

visualization consists of spheres and links whose

properties are given by the association rule

parameters. Each sphere represents an item and his

size and the color represent his contribution to the

rule. The sphere size represents the Information Gain

(Freitas, 1998) of the item and color shows if the

gain is positive (blue) or negative (gray). Graphical

encoding should highlight items with high positive

contribution and those with high negative

contribution (both are interesting to the user).

The second type of interestingness measures

correspond to the metric associated with the rule

(support, confidence, etc.). This meta information

that describe the properties of the rule are quantitative

variables according to Bertin’s semiology (Bertin,

1984). Theoretically, it is possible to represent a large

number of metrics using visual variables appropriate

to the area of interest of each user. For example,

we can represent the confidence or the support by

a distance between the antecedent and the

consequence. The visual metaphor stresses the rules

with hight confidence or support (Figure 5).

Furthermore, complementary text labels appear

above each objects to give the name of the

corresponding item.

CONCLUSIONS

In this study, we propose a new association rule

metaphor allowing the visualization of attributes

com- posing the association rule. Also, it shows

attributes relationships and contribution of each one

of them. but merely developing only novel visual

metaphor id rarely sufficient to make new

discovery. In association rule extraction process, the

decision-maker is overwhelmed by the association

rule algorithms results. Representing these results as

static images limits the visualization usefulness.

This explains why the user need to be able to

interact with the association rules representation in

order to find relevant knowledge. Interaction allows

also the user integration in the association rule

extraction process. The user should be able to

manipulate the extraction rules algorithms and not

only the graphical representations. This allows to

focus on interesting knowledge from the user point

of view, in order to make the association rule methods

be more generically useful to users. Our future works

will mainly concern the development of a human-

centered tool for rules extraction and manipulation

and the implementing a new operators of interesting

association rule extraction.

REFERENCES

Agrawal, R., Imielinski, T., and Swami, A. (1993). Mining

association rules between sets of items in large

databases. In Proceedings of the 1993 ACM SIGMOD

international conference on Management of data,

pages 207 – 216.

A NEW VISUALIZATION METAPHOR FOR ASSOCIATION RULES

807

Bertin, J. (1984). Semiology of Graphics: Diagrams,

Networks, Maps. University of Wisconsin Press.

Blanchard, J., Guillet, F., and Briand, H. (2007).

Interactive visual exploration of association rules with

rule-focusing methodology. Knowledge and

Information Systems, 13(1):43–75.

Bruzzese, D. and Buono, P. (2004). Combining visual

techniques for association rules exploration. In

AVI’04: Proceedings of the working conference on

Advanced visual interfaces, pages 381–384, New

York, NY, USA. ACM.

Chanda, P., and A. Zhang, J. Y., and Ramanathan, M.

(2010). On Mining Statistically Significant Attribute

Association Information. In SDM, pages 141–152.

Couturier, O., Hamrouni, T., Yahia, S. B., and Nguifo, E.

M. (2007). A scalable association rule visualization to-

wards displaying large amounts of knowledge. In

IV’07: Proceedings of the 11th International

Conference Information Visualization, pages 657–663,

Washington, DC, USA. IEEE Computer Society.

Freitas, A. A. (1998). On objective measures of rule

surprisingness. pages 1–9.

Freitas, A. A. (2001). Understanding the crucial role of

attributeinteraction in data mining. Artif. Intell. Rev.,

16(3):177–199.

Gordal and Demiriz, A. (2006). A framework for

visualizing association mining results. Lecture Notes

in Computer Science, pages 593–602.

Hendley, R. J., Drew, N. S., Wood, A. M., and Beale, R.

(1999). Narcissus: visualising information. In

Proceedings of the IEEE Symposium on Information

Visualization (INFOVIS ’95), pages 90–96. Morgan

Kaufmann Publishers Inc.

Imielinski, T. and Virmani, A. (1998). Association rules...

and what’s next? – towards second generation data

mining systems. Advances in Databases and

Information Systems, 1475:6.

Kopanakis, I. and Theodoulidis, B. (2003). Visual data

mining modeling techniques for the visualization of

mining outcomes. Journal of Visual Languages &

Computing, 14(6):543–589.

Liu, Y. and Salvendy, G. (2006). Design and evaluation of

visualization support to facilitate association rules

modeling. International Journal of Human Computer

Interaction, 21(1):15–38.

Provost, F. J. and Aronis, J. M. (1996). Scaling up

inductive learning with massive parallelism. Machine

Learning, 3(1):33–46.

Simoff, S. J., Bo¨ hlen, M. H., and Mazeika, A. (2008).

Visual data mining. Chapter Visual Data Mining: An

Introduction and Overview, pages 1–12. Springer-

Verlag, Berlin, Heidelberg.

IVAPP 2012 - International Conference on Information Visualization Theory and Applications

808