
Parallel Finite State Machines for Very Fast Distributable Regular
Expression Matching
Luis Quesada, Fernando Berzal and Francisco J. Cortijo
Department of Computer Science and Artificial Intelligence, CITIC, University of Granada, Granada 18071, Spain
Keywords:
Parallel Finite State Machine, PFSM, Regular Expressions, Automaton, Distributable.
Abstract:
Regular expressions provide a flexible means for matching strings and they are often used in data-intensive
applications. They are formally equivalent to either deterministic finite automata (DFAs) or nondeterministic
finite automata (NFAs). Both DFAs and NFAs are affected by two problems known as amnesia and acalculia,
and DFAs are also affected by a problem known as insomnia. Existing techniques require an automata conver-
sion and compaction step that prevents the use of existing automaton databases and hinders the maintenance of
the resulting compact automata. In this paper, we propose Parallel Finite State Machines (PFSMs), which are
able to run any DFA- or NFA-like state machines without a previous conversion or compaction step. PFSMs
report, online, all the matches found within an input string and they solve the three aforementioned problems.
Parallel Finite State Machines require quadratic time and linear memory and they are distributable. Parallel
Finite State Machines make very fast distributed regular expression matching in data-intensive applications
feasible.
1 INTRODUCTION
A regular expression, commonly called regex, pro-
vides a flexible means for matching strings (Aho,
1990) often used in data-intensive applications such
as lexical analysis in language processors (Levine
et al., 1992; Quesada et al., 2011), XML tokenization
(Hosoya and Pierce, 2007), bibliographic search (Aho
and Corasick, 1975), virus detection (Lee, 2007),
and other data mining applications (Han et al., 2006;
G´omez and Vaisman, 2008).
Regex matching relies on either deterministic fi-
nite automata (DFAs) or nondeterministic finite au-
tomata (NFAs) (Hopcroft et al., 2007). Both DFAs
and NFAs suffer from amnesia and acalculia, and
DFAs also suffer from insomnia (Kumar et al., 2007).
Amnesia is the inability to consider the progress of
multiple partial matches. Acalculia is the inability to
find subexpression occurrences. Insomnia is the in-
ability to unload from memory rarely used big por-
tions of automata when not needed.
Several techniques exist that solve those problems
by converting sets of regular expressions into com-
pact state machines (Pasetto et al., 2010; Becchi and
Cadambi, 2007; Kumar et al., 2006; Ficara et al.,
2008). The required conversion or compaction step
preventsusing existing automata that could be already
available in antivirus signature databases or complex
data filters. It also makes the modification of the set of
regular expressions more difficult, as the conversion
and compactionsteps have to be performedevery time
they are modified.
In this paper, we propose Parallel Finite State Ma-
chines (PFSMs). A Parallel Finite State Machine is
an automaton that can have multiple active states. It
can be used for efficiently finding all the matches of a
set of regular expressions in a given input string, and
it solves the amnesia and acalculia problems. They
also mitigate the effect of insomnia by reducing the
number of states in the resulting automaton.
Parallel Finite State Machines do not require con-
version and compaction steps and they can, therefore,
be run on existing DFAs or NFAs. They also allow the
efficient addition or removal of regular expressions
from existing automata.
Parallel Finite State Machines can perform reg-
ular expression matching in quadratic order of effi-
ciency and have linear memory space requirements,
apart from automata storage, in the worst case. More-
over, they allow the parallelization of the regular ex-
pression matching process with almost linear scala-
bility in the practice.
105
Quesada L., Berzal F. and J. Cortijo F..
Parallel Finite State Machines for Very Fast Distributable Regular Expression Matching.
DOI: 10.5220/0003949901050110
In Proceedings of the 7th International Conference on Software Paradigm Trends (ICSOFT-2012), pages 105-110
ISBN: 978-989-8565-19-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 BACKGROUND
A DFA is a tuple (Σ, Q, q
0
, δ, F), where:
• Σ is the input alphabet (i.e. a finite, non-empty set
of symbols).
• Q is a finite, non-empty set of states.
• q
0
is an initial state, an element of Q.
• δ is the state-transition function: δ : Q× Σ → Q.
• F is the set of final states, a subset of Q.
In a NFA, the state-transition function would be
δ : Q× Σ → P (Q). That is, δ returns a set of states.
NFA-like state machines can be converted into
DFA-like machines by expanding their states and re-
moving any nondeterminism (Sipser, 2005). Each
state in the DFA will correspond to a set of states in
the NFA. Although DFAs are faster than NFAs, there
can be up to O(2
n
) states in a DFA, being n the num-
ber of states in the NFA.
Amnesia can be inefficiently solved by using a
separate state for each combination of every poten-
tially simultaneous partial match (Kumar et al., 2007).
Somehow, this is analogous the approach of con-
verting NFAs into DFAs, but much more memory-
intensive and therefore, quite impractical.
Acalculia can be solved by repeating the whole
regex matching process for each input string index as
a starting position and stopping at each possible end-
ing position (Quesada et al., 2011). This solution is
time-intensive and does not allow for the progress of
partial matches to be simultaneously considered, thus
preventing the solution of amnesia.
When the number of states in an automaton in-
creases, as a result of converting a NFA into a DFA
or considering simultaneous partial matches, mem-
ory use skyrockets and insomnia has to be taken into
consideration. Insomnia can be solved by swapping
rarely used portions of automata out to the hard drive
when they have not been used for a while (Kumar
et al., 2007). However, that approach presents two
major drawbacks. When those portions are used back
again, there might be a swapping delay. Also, au-
tomata might be so huge that even swapping it to hard
drive could be impractical. The most common ap-
proach in practice consists of avoiding the expansion
of states (Kumar et al., 2006; Ficara et al., 2008; Bec-
chi and Cadambi, 2007), thus eliminating the major
cause of insomnia.
DotStar (Pasetto et al., 2010) solves amnesia and
acalculia by converting sets of regular expressions
into compact state machines pertaining to a subclass
of DFA with status bits associated to their states.
The technique proposed in (Becchi and Cadambi,
2007) reduces the memory requirement of DFAs by
merging non-equivalent states and labelling their in-
put and output transitions.
D
2
FAs (Kumar et al., 2006) reduce the memory
requirement of DFAs by assuming default transitions
for all the states. Default transitions differ from ep-
silon transitions in that, in case a state cannot find
a transition for a specific input symbol, the default
transition will be followed and a transition with that
specific input symbol will be looked for in the target
state. Several default transitions could be followed for
processing a single symbol.
δFA (Ficara et al., 2008) is an extension of D
2
FA
that determines some of the results of chaining de-
fault transitions and non-defaulttransitions and makes
them explicit in the automaton for optimization. It
also uses local memory to store the set of transitions
going out from a state that is the source of a default
transition. If the default transition of the target state
brings to the source state, the transition set is known
without having to follow the default transition back to
the source state.
These techniques require a conversion or com-
paction step that makes them unable to run on existing
uncompacted DFA- or NFA-like state machines that
could be already available in automaton databases.
Moreover, compaction forbids regular expressions to
be added or removed from the state machine directly.
Therefore, compaction hampers the maintainability of
the automata. It should be noted that the only way to
add or remove regular expressions from the state ma-
chine would involve converting and compacting the
whole new regular expression set, which is costly in
terms of time when the set of regular expressions is
complex.
Lamb (Quesada et al., 2011) is a lexical analyzer
that partially solves acalculia by greedily matching
every pattern starting at every position of the input
string. However, it does not find all the possible
submatches, as greedily-matched regular expressions
find the longest possible matching and discard any
shorter matchings. That is, even though Lamb finds
matchings starting at any position in the input string,
it does not finds matchings ending at different posi-
tions in the input string for the same starting posi-
tion. This implies that some matchings may indeed
be missed (i.e. Lamb still suffers from acalculia).
3 PARALLEL FINITE STATE
MACHINE
In order to solve the amnesia, the acalculia, and the
insomnia problems, we propose the use of Parallel Fi-
nite State Machines (PFSMs).
ICSOFT2012-7thInternationalConferenceonSoftwareParadigmTrends
106

3.1 Definition
A PFSM is a concurrent automaton in which several
states may be active at the same time and final states
include associated labels. This feature enables match-
ing an input string at several starting positions with a
set of regular expressions in order to find all the pos-
sible matches. A PFSM generalizes all existing com-
binations of DFA- and NFA-like state machines.
A PFSM is a tuple (Σ, Q, q
0
, δ, F, L, l), where:
• Σ is the input alphabet.
• Q is a finite, non-empty set of states.
• q
0
is an initial state, an element of Q.
• δ is a NFA-like state-transition function: δ : Q ×
Σ → P (Q).
• F is the set of final states, a subset of Q.
• L is the set of labels that identify the different reg-
ular expressions.
• l is the state-label function: l : F → L.
A set of DFAs or NFAs representing different reg-
ular expressions can be put together by using an an-
cillary initial state with epsilon transitions to each of
the initial states of the different automata, and by as-
signing each final state a label identifying that iden-
tifies the regular expression it represents. The result-
ing automata, including the ancillary initial state and
the added epsilon transitions, conform the PFSM. It
should be noted that NFAs can be considered instead
of DFAs for some regular expressions in order to trade
off processing time for memory use.
For example, an automaton that considers the reg-
ular expressions “a*c”, “ac”, and “a(ca)*b” is shown
in Figure 1. When trying to match the input string
“aacacab”, that automaton returns all the matches
shown in Figure 2.
b
a
a
ε
c
a
ε
c
c
ε
qinit
aq0
aq1
a*c
bq0 bq1 bq2
ac
cq0
cq1
cq3
a(ca)*b
Figure 1: A PFSM that compiles the “a*c”, “ac”, and
“a(ca)*b” regular expressions.
As the whole automaton does not need to be con-
verted into a single DFA, it does not have to be ex-
panded with too many states, which cuts down its
INPUT: "aacacab"
"a*c" matches [0-2]: "aac"
"a*c" matches [1-2]: "ac"
"ac" matches [1-2]: "ac"
"a*c" matches [2-2]: "c"
"a*c" matches [3-4]: "ac"
"ac" matches [3-4]: "ac"
"a*c" matches [4-4]: "c"
"a(ca)*b" matches [1-6]: "acacab"
"a(ca)*b" matches [3-6]: "acab"
"a(ca)*b" matches [5-6]: "ab"
Figure 2: Results of matching the “aacacab” input string
using the PFSM in Figure 1.
memory requirements, thus mitigating the impact of
insomnia.
Also, as amnesia is solved by allowing several si-
multaneously active states that can represent parallel
partial matchings, it is unnecessary to expand the au-
tomaton with states representing different simultane-
ous partial matchings. This drastically reduces the
impact of insomnia.
Furthermore, as the automaton does not need to
be compacted, regular expressions can be efficiently
added or removed from a PFSM. This makes PFSM
maintenance easier.
3.2 Algorithm
A PFSM is initialized by activating the initial state
at the start of the input string. It is also reinitialized
every time an input symbol is going to be processed,
in order to consider simultaneous partial matchings
starting at different positions in the input string.
Whenever the automaton is initialized or reinitial-
ized, the initial state is activated and it is annotated
with a tag that represents the current input string po-
sition, which will be used when a match is completed
in order to know the starting position of the matched
substring. The tag will be propagated unmodified to
other states when applying transitions, and a state can
include several tags at any given time, which will cor-
respond to multiple simultaneous matches starting at
different input string positions. It should be noted
that, whenever the automaton is reinitialized, any ac-
tive states are kept active.
Using a PFSM, each input symbol is processed in
four steps:
1. The automaton is initialized or reinitialized by ac-
tivating the initial state and tagging it with the cur-
rent input string position.
2. All epsilon transitions from the active states (e.g.
the initial ancillary state) are iteratively applied
and the target states of those transitions are
tagged.
ParallelFiniteStateMachinesforVeryFastDistributableRegularExpressionMatching
107

3. The input symbol is consumed and, from all the
transitions from the active states, only those that
match the current symbol are traversed.
4. The traversed transitions are applied and the target
states of those transitions are tagged.
Figure 3 shows how the PFSM from Figure 1 con-
sumes the two symbols in the “ac” input string.
Whenever a transition is applied, in the second or
fourth step of the algorithm above, the target state is
checked. When it is final, a matching has been found.
The matching starting position is given by the final
state tag (or tags). The matching ending position is
the current input string position. The matched regular
expression is identified by the label of the final state.
3.3 Efficiency Analysis
Given an alphabet with s symbols and r regular ex-
pressions, being m the maximum number of states
of an automaton representing a regular expression,
a PFSM will contain mr + 1 states. A maximum of
n
2
r matchings will be performed in an input string of
length n.
If regular expressions are implemented as DFAs,
the resulting PFSM automaton may contain up to mr
states and mrs transitions. At most, r states may be
active when considering a single symbol of the input
string. As matchings starting at different input string
positions are considered, O(nr) states may be active
in the PFSM at any given time. The PFSM processes
one symbol at a time, so the process is repeated for
the n symbols in the input string. Therefore, PFSMs’
efficiency is O(n
2
r) in time and O(nr+ mrs) in space.
If regular expressions are implemented as NFAs,
the resulting PFSM automaton may contain up to mr
states and m
2
rs transitions. At most, mr states may be
active when considering a single symbol of the input
string. As matchings starting at different input string
positions are considered, O(nmr) states may be active
in the PFSM at any given time. The PFSM processes
one symbol at a time, so the process is repeated for
the n symbols in the input string. Therefore, PFSMs’
efficiency is O(n
2
mr) in time and O(nmr + m
2
rs) in
space.
Our suggested implementation of PFSMs allows
trading off time for space by expressing some of the
regular expressions as NFAs instead of DFAs.
It should be noted that PFSMs, as described here,
can be implemented as Moore-like machines. A
Mealy-like implementation would yield no reduction
on the number of states and would decrease the effi-
ciency of the PFSM implementation both in terms of
time and space.
3.4 Parallelization
The PFSM is a parallelizable automaton with an al-
most linear scalability.
3.4.1 Regular Expression Partitioning
PFSMs can be partitioned by distributing the set of
regular expressions among the different processors.
Each processor will find the matches within a subset
of regular expressions, which reduces the automaton
size at a given processor. By following this approach,
the memory use at a given processor can be reduced
just to the space that is necessary to store a single reg-
ular expression. Although the idea of PFSM partition-
ing is trivial, the fact that PFSM does not compact the
regular expression set that allows this kind of paral-
lelization on the fly, in contrast to existing techniques
that need to distribute the regular expression set and
compact each subset separately.
Furthermore, when some regular expressions are
expressed as NFAs in order to save memory, it is pos-
sible to distribute both NFA and DFA regular expres-
sions among processors in such a way that memory
use and processing time is balanced in each proces-
sor, as proposed in (Sun et al., 2010).
3.4.2 Data Partitioning
PFSMs can be partitioned by distributing the input
string among the different processor. Two different
approaches are proposed:
• Lazy Data Partitioning. The input string is scat-
tered among the different processors. Each pro-
cessor will find the matches that start within its
segment of the input string and end either in or
after that segment. To achieve this, the automa-
ton reinitialization is disabled after surpassing the
ending position of the segment, but the process-
ing does not stop until the end of the input string
is reached or there are no active states. Each pro-
cessor may need to ask other processors for their
segment in order to finish its processing.
• Chained Data Partitioning. The input string is
scattered among the different processors. Each
processor will find the matches that start and end
within its segment. The tagged active states at the
end of the processing are sent to the next proces-
sor, a different set of tagged active states are re-
ceived from the previous processor and the whole
cycle is repeated (without reinitializations) until
no more tagged active states are received from the
previous processor.
ICSOFT2012-7thInternationalConferenceonSoftwareParadigmTrends
108
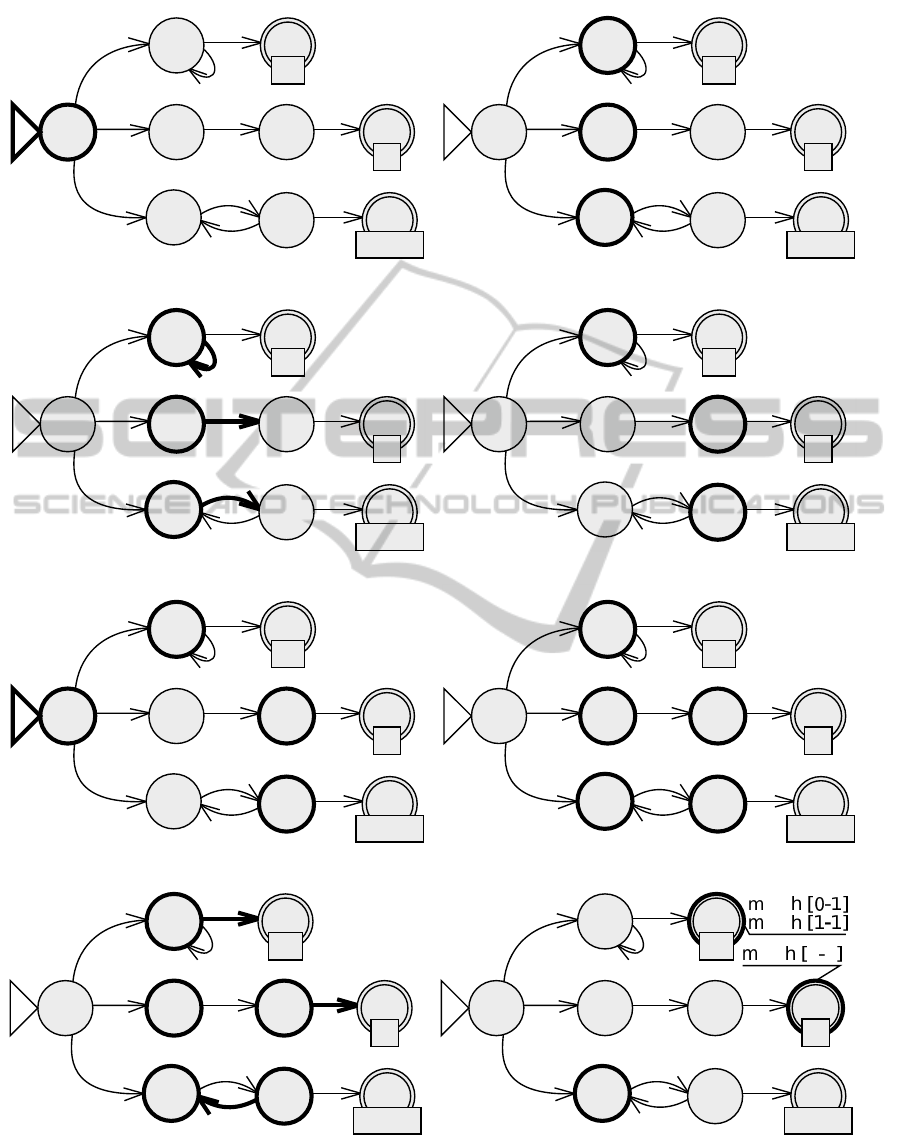
b
a
a
ε
c
a
ε
c
c
ε
qinit
aq0
aq1
a*c
bq0 bq1 bq2
ac
cq0
cq1
cq3
a(ca)*b
(0)
(a) Initialization (input[0] is ’a’).
b
a
a
ε
c
a
ε
c
c
ε
qinit
aq0
aq1
a*c
bq0 bq1 bq2
ac
cq0
cq1
cq3
a(ca)*b
(0)
(0)
(0)
(b) Application of epsilon transitions.
b
a
a
ε
c
a
ε
c
c
ε
qinit
aq0
aq1
a*c
bq0 bq1 bq2
ac
cq0
cq1
cq3
a(ca)*b
(0)
(0)
(0)
(c) Transitions matching ’a’.
b
a
a
ε
c
a
ε
c
c
ε
qinit
aq0
aq1
a*c
bq0 bq1 bq2
ac
cq0
cq1
cq3
a(ca)*b
(0)
(0)
(0)
(d) Application of transitions.
b
a
a
ε
c
a
ε
c
c
ε
qinit
aq0
aq1
a*c
bq0 bq1 bq2
ac
cq0
cq1
cq3
a(ca)*b
(0)
(0)
(0)
(1)
(e) Reinitialization (input[1] is ’c’).
b
a
a
ε
c
a
ε
c
c
ε
qinit
aq0
aq1
a*c
bq0 bq1 bq2
ac
cq0
cq1
cq3
a(ca)*b
(0,1)
(0)
(0)
(1)
(1)
(f) Application of epsilon transitions.
b
a
a
ε
c
a
ε
c
c
ε
qinit
aq0
aq1
a*c
bq0 bq1 bq2
ac
cq0
cq1
cq3
a(ca)*b
(0,1)
(0)
(0)
(1)
(1)
(g) Transitions matching ’c’.
b
a
a
ε
c
a
ε
c
c
ε
qinit
aq0
aq1
a*c
bq0 bq1 bq2
ac
cq0
cq1
cq3
a(ca)*b
(0,1)
(0)
(0)
atc 0 1
atc
atc
(h) Application of transitions. Three matches ending at in-
dex 1 are found.
Figure 3: Example PFSM running for two full cycles. The final state labels specify which regular expression that state
corresponds to. Active states and transitions are shown in bold. The numbers between parentheses are the valid starting
positions for the states.
ParallelFiniteStateMachinesforVeryFastDistributableRegularExpressionMatching
109

Data partitioning linearly reduces memory use
with respect to the number of processors. Assuming a
maximum match length of twice the segment length,
data partitioning also reduces processing time linearly
with respect to the number of processors.
4 CONCLUSIONS AND FUTURE
WORK
Regular expressions provide a flexible means for
matching strings and they are often used in data-
intensive applications.
The implementation of regular expression match-
ing typically relies on deterministic finite automata
(DFAs) or nondeterministic finite automata (NFAs).
Both DFAs and NFAs are affected by amnesia and
acalculia, and DFAs also suffer from insomnia.
Techniques exist that solve those problems by
converting sets of regular expressions into compact
state machines. This approach, however, presents two
major drawbacks: it prevents the use of existing au-
tomata that could be already available in antivirus sig-
nature databases or complexdata filters; and it hinders
the maintenance of the resulting automata, since the
whole set has to be converted and compacted again
whenever a regular expression has to be added or re-
moved from the set.
We have proposed Parallel Finite State Machines
(PFSMs), which allow multiple active states and effi-
ciently find all the matches of regular expressions in
an input string, solving amnesia and acalculia. PF-
SMs also mitigate the effect of insomnia by reducing
the number of states in the resulting automaton.
As PFSMs do not require any conversion or com-
paction step, they are able to run on existing DFA-
or NFA-like machines, and they allow the addition or
removal of regular expressions with zero downtime,
making the maintenance of the automaton easier.
PFSMs can perform regular expression matching
in quadratic time and have linear memory space re-
quirements, apart from automata storage, in the worst
case. On top of that, PFSMs support three different
approaches for parallelization with almost linear scal-
ability in the practice.
Therefore, PFSMs make very fast distributed reg-
ular expression matching in data-intensive applica-
tions feasible.
We plan to apply PFSMs to improve the Lamb
lexical analyzer and cure it from its partial acalculia.
We also plan to apply PFSMs to data-intensivepattern
matching applications.
ACKNOWLEDGEMENTS
Work partially supported by research project
TIN2009-08296.
REFERENCES
Aho, A. V. (1990). Algorithms for finding patterns in
strings, volume A, pages 255–300. MIT Press, Cam-
bridge, MA, USA.
Aho, A. V. and Corasick, M. J. (1975). Efficient string
matching: An aid to bibliographic search. Commu-
nications of the ACM, 18(6):333–340.
Becchi, M. and Cadambi, S. (2007). Memory-efficient reg-
ular expression search using state merging. In Proc.
of the IEEE INFOCOM’2007, pages 1064–1072.
Ficara, D., Giordano, S., Procissi, G., Vitucci, F., Antichi,
G., and Pietro, A. D. (2008). An improved DFA for
fast regular expression matching. ACM SIGCOMM
Computer Communication Review, 38(5):31–40.
G´omez, L. I. and Vaisman, A. A. (2008). RE-SPaM: Us-
ing regular expressions for sequential pattern min-
ing in trajectory databases. In Proc. of the IEEE
ICDMW’2008, pages 395–398.
Han, J., Kamber, M., and Pei, J. (2006). Data Mining: Con-
cepts and Techniques. Morgan Kaufmann, 2nd edi-
tion.
Hopcroft, J. E., Motwani, R., and Ullman, J. D. (2007). In-
troduction to Automata Theory, Languages, and Com-
putation. Pearson Education, 3rd edition.
Hosoya, H. and Pierce, B. (2007). Regular expression
pattern matching for XML. In Proc. of the ACM
SIGPLAN-SIGACT POPL’2007, volume 36 of ACM
SIGPLAN Notices, pages 67–80.
Kumar, S., Chandrasekaran, B., Turner, J., and Varghese,
G. (2007). Curing regular expressiong matching algo-
rithms from insomnia, amnesia and acalculia. In Proc.
of the ACM/IEEE ANCS’2007, pages 155–164.
Kumar, S., Turner, J., and Williams, J. (2006). Advanced al-
gorithms for fast and scalable deep packet inspection.
In Proc. of the ACM/IEEE ANCS’2006, pages 81–92.
Lee, T.-H. (2007). Generalized Aho-Corasick algorithm for
signature based anti-virus applications. In Proc. of the
ICCCN’2007, pages 792–797.
Levine, J. R., Mason, T., and Brown, D. (1992). lex & yacc.
O’Reilly, 2nd edition.
Pasetto, D., Petrini, F., and Agarwal, V. (2010). Tools
for very fast regular expression matching. Computer,
43(3):50–58.
Quesada, L., Berzal, F., and Cortijo, F. J. (2011). Lamb: A
lexical analyzer with ambiguity support. In Proc. of
the ICSOFT’2011, volume 1, pages 297–300.
Sipser, M. (2005). Introduction to the Theory of Computa-
tion. Course Technology, 2nd edition.
Sun, Y., Liu, H., Valgenti, V. C., and Kim, M. S. (2010).
Hybrid regular expression matching for deep packet
inspection on multi-core architecture. In Proc. of the
ICCCN’2010, pages 1–7.
ICSOFT2012-7thInternationalConferenceonSoftwareParadigmTrends
110
