
A VIRTUAL MACHINES PLACEMENT MODEL FOR ENERGY
AWARE CLOUD COMPUTING
Paolo Campegiani
University of Rome Tor Vergata, Rome, Italy
Keywords:
Cloud, Green Computing, Virtual Machines Placement, Service Level Agreements, Resources Allocation,
TCO, Genetic Algorithm, Bin Packing.
Abstract:
We present an energy aware model for virtual machines placement in cloud computing systems. Our model
manages resources of different kind (like CPU and memory) and energy costs that are depending on the kind
and amount of deployed resources, incorporating capital expenses (costs of infrastructure and amortizations),
operational expenses (electricity costs) and data center energy parameters as PUE, also with possibly different
service levels for virtual machines. We show that the resulting model could be solved via a genetic algorithm,
and we perform some sensitivity analysis on the model energy parameters.
1 INTRODUCTION
Server farms consume a significant portion of the total
electricity, with an annual cost of several billions. The
explosive growth of the cloud computing paradigm,
where the economies of scale are one of the main eco-
nomic driving forces, suggests that any general strat-
egy to reduce energy consumption should take into
account these immense cloud data centers, with the
typical usage scenarios characterizing this kind of in-
frastructures.
In this article we present a model that connects
the energy consumption of a cloud architecture to the
fees requested by the Cloud Service Provider (CSP)
and payed by the Cloud Service Customer (CSC).
The model extends some previous works, (Campe-
giani and LoPresti, 2009) and (Campegiani, 2009),
where the problem of virtual machine placement was
considered in a most general way. We build on this
generality to express and capture a fine-grain account-
ing of energy consumption.
We made the following key contributions: a) we
develop an energy model consumption for cloud ar-
chitectures that takes into account different kinds of
resources consumption; b) we connect this model
(that is more oriented towards operational expenses
control) to a model that is more focused on capital
expenses, resulting in a general model that accounts
for global Total Cost of Ownership (TCO) of a cloud
computing infrastructure, then performing some ini-
tial sensitivity analysis of the energy related parame-
ters.
This paper is organized as follows: on section 2
we present some energy models relating energy con-
sumption to resources usage, focusing first on sin-
gle systems and then on cloud systems; on section
3, we present some models for resources allocation
in cloud computing architectures; on section 4 we ex-
tend one of these model to include energy consump-
tion into it, defining an optimizationproblem that con-
siders both capital expenses (i.e., hardware procure-
ment, data center setup) and operational expenses (i.e.
electricity bill) extending a previously defined heuris-
tic and a genetic algorithm (GA) to deal with this new
optimization problem, that happens to be NP-hard; on
section 5 we present a specific instance of the prob-
lem, based on our own experience of real cloud ar-
chitectures; on section 6 we present the results, also
performing some sensitivity analysis on the energy re-
lated parameters of the model. We then briefly con-
clude on section 7.
2 SYSTEM ENERGY MODELS
We briefly present some energy consumption models,
both for single and distributed systems. (Singh et al.,
2009) has a linear powermodel based on the hardware
performance counters of the processor. Performance
counters for the model are chosen considering the ac-
tual physical implementation of the processor die, and
247
Campegiani P..
A VIRTUAL MACHINES PLACEMENT MODEL FOR ENERGY AWARE CLOUD COMPUTING.
DOI: 10.5220/0003950402470253
In Proceedings of the 1st International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2012), pages 247-253
ISBN: 978-989-8565-09-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

the power estimation error is between 0 and 15% for
many different benchmarks, including the SPEC 2006
suite. (Economou et al., 2006) models the energy
consumption of a server as a linear model of CPU,
memory, disk and network utilization. The predic-
tion error is almost below 5% for all the validation
benchmarks. (Rivoire et al., 2008) compares different
full-system power models, with the key observation
that multi-dimensional models (disk and performance
counter based) performs better that models based only
on CPU usage. (McCullogh et al., 2010) evaluates the
effectivenessof some power models. As the complex-
ity of current processors increases, linear models fits
poorly, but the article itself notes that the 2-6% error
made from linear models is well within the accuracy
for tasks like data center server consolidation.
Many models for allocating resources for cloud com-
puting have been developed to be energy aware. Al-
most all consider only CPU as the resource to be
allocated, and the power model is typically linear,
with a server idle power around 50-70% of the peak
power. Some of these models take into account the
critical Power Usage Effectiveness (PUE) parameter,
that defines the total amount of electricity required by
a data center, which is made up of what’s required
for cooling, general operations, lost on the transmis-
sion lines or by the AC/DC conversion. It’s widely
known that the lowest PUE is on Google data centers,
and is around 1.2 (which means that for each 1 kW
required to power on the computing resources, only
additional 0.2 kW are required for cooling and every-
thing else), where a typical PUE for a standard data
center is around 1.4-1.7, and for an enterprise data
center could climb up to 2.0-3.0.
(Cardosa et al., 2009) considers only CPU as the
resources to be allocated in a cloud environment, with
a fixed cost for each server turned on. With such as-
sumptions, the optimization model tries to reduce the
number of servers to be allocated. (Gandhi et al.,
2009) relates the CPU power to the frequency, with
a fixed minimum to account for idle systems. Even
if a cubic curve fits better the empirical data, a linear
fit is also deemed as sufficiently accurate. (Urgaonkar
et al., 2010) considers a quadratic model that relates
the CPU usage to the system power, considering an
offset accounting for the idle power of the system
around 65% of the peak power. (Mazzucco and Du-
mas, 2011) considers the power drained of the CPU
as a linear function of the load, with an idle power of
about 65%. (Srikanthaiah et al., 2008) develops an
empirical model that relates the system’s overall en-
ergy consumption to both CPU and disk utilization,
finding that the optimal combination that minimizes
the energy for computed transaction is around 70%
CPU and 50% disk utilization. From this on it devel-
ops an optimization problem as a multi-dimensional
bin-packing problem.
3 RESOURCE ALLOCATION FOR
CLOUD SYSTEMS
We briefly recall some strategies for resource allo-
cation on cloud computing platforms. At this level,
resource allocation is defined as a virtual machine
placement problem: considering a set of virtual ma-
chines, what is the best way to place them into some
powerful physical hosts? This consolidation process
aims to achieve operational efficiency, increasing the
usage of physical resources: each physical host typ-
ically allows for some virtual machines to be placed
into it. Even if this could result in contention of phys-
ical resources (usually mitigated by the Virtual Ma-
chine Monitor), the savings are economically sound-
ing for the CSP, which could offer a competitive price
for the use of its resources, usually with an hour gran-
ularity for the rent and without upfront costs for the
CSC. The CSP has also operational costs, including
the electricity bill, that on the contrary are affected
by this consolidation process: a physical hosts offer-
ing computing power to fewer virtual machines con-
sumes less power than an almost fully loaded hosts.
This means that the CSP must carefully balance be-
tween this somehow conflicting goals. (Beloglazov
and Buyya, 2010) considers only CPU, and models
the problem as a bin packing optimization, where the
different physical servers use Dynamic Voltage Fre-
quency Scaling (DVFS) to change their CPU frequen-
cies according to the amount of virtual machines al-
located over them. (Lu and Gu, 2011) has a multi-
dimensional model of resources allocations, and op-
timizes it using an ant-colony algorithm. (Chang
et al., 2010) considers that the available virtual ma-
chines from a CSP are fixed in size, so the problem is
to map these allowed capacities into a set of virtual
machines requirements, avoiding unnecessary over-
provisioning and reducing migration overhead. The
lack of available dataset forces the authors to compare
the different algorithms only in relative terms.
4 FORMAL MODEL
We consider the point of view of the CSP: the CSC
has submitted a lists of virtual machines requirements
(in terms of CPUs, memory, I/O and network guar-
anteed bandwidth). Some (or all) of these virtual
SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems
248

machines have different and increasing Service Level
Agreements (SLAs) for them, where the CSC is will-
ing to pay more for more resources (as an example,
more processors for an application server, or more
I/O bandwidth for the web server). This list would
change, as an example on an hourly basis, so the CSP
must react determining both the level of provided ser-
vices (more or less powerful virtual machines) and
where to allocate them, minimizing both the number
of systems and the energy consumption.
The model proposed is an extension of the multi-
dimensional model presented in (Campegiani and Lo-
Presti, 2009) and (Campegiani, 2009). We extend the
model to allow for an objective function (which is the
profit for the CSP) that takes into account the energy
consumption of the allocated virtual machines. In the
original model, the objective function was defined as:
P =
G
∑
i=1
g
i
∑
j=1
M
∑
m=1
x
ij
m
P
Ia
− C∗
M
∑
m=1
u
m
(1)
In this model, virtual machines are arranged in
tiers, labeled from 1 to g. A solution of the problem
must allocate all machines from each tier, but could
choose a different SLA for each single different ma-
chine (virtual machines from tier i have g
i
different
SLAs); in the context of this paper we have classes of
virtual machines (see table 1) instead of tiers, but the
allocation problem is similar and it will be extended
to include the energy related costs.
In eq. 1 we have that:
• P is the total profit for the CSP;
• G is the number of different classes of virtual ma-
chines;
• M is the number of different physical servers;
• x
ij
m
is a decision variable that maps if the i-th vir-
tual machines with the SLA j-th is allocated on
the physical server m;
• u
m
is an auxiliary variable that maps whether the
m server is used or not;
• C is the (amortized) hourly cost of a single physi-
cal server.
The constraints are omitted for brevity: they de-
fine the problem as a bin packing problem (we want
to minimize the number of servers), that is also
multi-dimensional (we deal with different kind of re-
sources) and also multiple-choice (we want one and
one only SLA for each virtual machine to be hosted
on the physical servers); these constraints are further
discussed in (Campegiani and LoPresti, 2009) and
(Campegiani, 2009).
To model energy costs, we start defining these
three elements:
• IDLE
total
defined as the idle power of all the M
servers (if a server is not used, it could be easily
turned off, reducing the number of physical hosts
to M − 1);
• CPU
total
defined as the power required to power
up all the CPUs required by all the allocated vir-
tual machines;
• MEM
total
defined as the power required to power
up all the memory required by all the allocated
virtual machines.
For a virtual machine (ij) (i.e., the i-th virtual ma-
chine with j-th SLA) we explicitly define CPU
ij
and
MEM
ij
as the requested amount of CPUs and mem-
ory, respectively. Also we express CPU and MEM
as the energy costs of one unit of CPU and mem-
ory, respectively. These costs are on average all over
the infrastructure; our assumption is that each virtual
machine increases the consumption of energy propor-
tionally to the amount of demanded virtual resources.
Taken all into account, we have that:
IDLE
total
= IDLE ∗
M
∑
m=1
u
m
(2)
CPU
total
= CPU ∗
G
∑
i=1
g
i
∑
j=1
CPU
ij
∗
M
∑
m=1
x
ij
m
(3)
MEM
total
= MEM ∗
G
∑
i=1
g
i
∑
j=1
MEM
ij
∗
M
∑
m=1
x
ij
m
(4)
Eq. 3 and 4 are a bit tricky; the last product term
is intended to nullify the index m, as in the context of
these equations we are only interested in evaluating
if CPU
ij
(or MEM
ij
) is allocated or not in the solu-
tion, because the energy consumption model is in fact
the same for each server. The total energy cost are
the sum of IDLE
total
, CPU
total
an MEM
total
times the
PUE times the cost of kWh (we are considering, for
simplicity, that each allocation slot lasts for one hour):
EnergyCost = PUE ∗ kWh∗
(IDLE
total
+CPU
total
+ MEM
total
) (5)
and finally the objective function that we have to
maximize is defined as:
P
′
= P− EnergyCost (6)
Eq. 6 allows the CSP to consider both capital ex-
penses (the cost C of each server) and operational
expenses (how much energy is required to power
up and cool the systems). The parameters of these
equations are discussed in the following section, and
AVIRTUALMACHINESPLACEMENTMODELFORENERGYAWARECLOUDCOMPUTING
249
they could change accordingly to market price fluc-
tuations. Other operational expenses (like personnel
costs) are omitted, but they are usually proportional
to other costs.
In order to solve this maximization problem,
we consider two energy-aware extensions of previ-
ously developed strategies, adapting and extending
the heuristic presented in (Campegiani and LoPresti,
2009) and the genetic algorithm (GA), presented in
(Campegiani and LoPresti, 2009), with some varia-
tions to account for the energy consumption and elec-
tricity costs.
5 DATASET
To the best of our knowledge, there aren’t shared
and publicly available datasets characterizing a cloud
computing architecture, so we have chosen to analyze
our model considering an hypothetical dataset (pre-
sented in tables 1, 2 and 3) that draws its origins from
authors’ on-field experience on real SME (Small and
Medium Enterprise) setups.
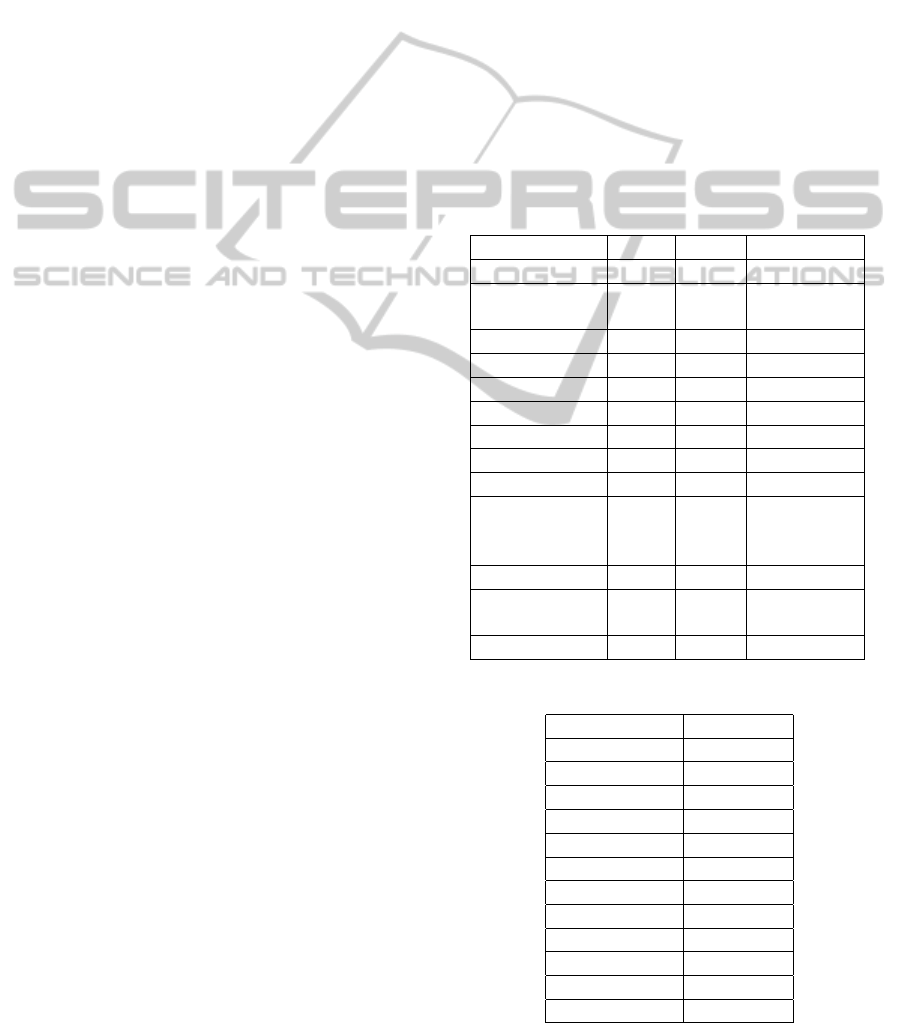
In table 1 each row captures the (possible) differ-
ent SLAs, modeled in term of CPU and memory re-
quirements, for a different kind of virtual machine.
A significant share of the total are virtualized desk-
tops, with different flavors for different kind of users
(i.e. a low level desktop would suffice for some cleri-
cal work, whilst an high level desktop is better suited
for some engineering work). Other systems are busi-
ness systems alike as application servers, email sys-
tems and so on. Some of these systems have different
possible SLAs (as an example, a low level desktop
could have 1 CPU and 1 GB of memory or 2 CPU
and 2 GB of memory). We have omitted disk re-
sources, as in a cloud computing environmentthey are
usually centralized on a NAS/SAN system, for which
we have not been able to find any sufficiently accu-
rate power consumption model. Network resources
are also omitted as they account for a very small part
of the energy consumption. In table 2 there are the
fees that the CSP earns when it allocates one virtual
machine of a specific kind with a specific SLA (i.e.,
the CSP earns 0.25 units of currency when it allocates
resources for a low level desktop with 1 CPU and 1
GB of RAM, but earns 0.5 units of currency when al-
locates resources for a low level desktop with 2 CPUs
and 2 GB of RAM). It is important to observe that
these fees are monotone non decreasing in each class
of virtual machines but not necessarily all over the
classes, and any linear relation between fees and the
number of CPUs or memory footprint is generally ap-
plicable but not always true. We have chosen these
fees considering some typical market prices from big
cloud vendors. Table 3 shows some parameters for
a medium blade system, comprised of 2 CPUs of 8
cores each, with each CPU absorbing at full power 90
W. The memory (64 GB) absorbs up to 20 W, and with
an idle power of 100 W the blade at full usage drains
300 W. PUE is set to 1.5 and 1 kWh costs 0.12 units
of currency. In our model we have 32 of these blades
to host virtual machines. As we are considering kWh
as the unit of energy cost, we are implying that the
optimization problem is evaluated on an hourly ba-
sis. On each of these allocation slots we could have a
change of some of the model parameters, as the price
of electricity during off-peak hours is quite lower than
during peak hours. We note that this istance of an NP-
hard problem as an excess of 11,000 decision vari-
ables.
Table 1: Types, numerosity and different SLAs for CPU and
memory requirements for the experimental testbed.
Class Num. CPUs Mem. (GB)
Low Desktop 70 1/2 1/2
Medium
Desktop
50 2/4 2/4
High Desktop 20 4/4 4/8
App Server 8 2/4/6 4/8/8
DB Server 2 2/4/4 4/8/8
Web Proxy 1 4/8 8/16
DSS 1 4 8
Web Server 10 2/4 2/4
File Server 1 1/1 2/4
Knowledge
Management
System
1 2/4 2/4
Intranet 1 1/2 1/2
Software Dis-
tribution
1 2/4 2/8
Email system 4 2/4 2/4
Table 2: Scenario 1: Fees for each class and SLAs.
Low Desktop 0.25/0.5
Med. Desktop 0.50/0.75
High Desktop 1/1.5
App Server 0.50/1.5/2
DB Server 0.5/1.5/1.5
Web Proxy 1.5/2.0
DSS 1.5
Web Server 0.25/0.5
File Server 0.25/0.5
Know. Mgt. 0.5/0.75
Intranet 0.2/0.5
Sw. Dist. 0.5/1.0
Email system 0.5/0.75
SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems
250

Table 3: Parameters for the server. The hourly cost of a
server is the procurement cost amortized over 5 years.
Parameter Value
Physical Host CPUs 16
Physical Host Memory 64 GB
Server Cost 15,000
Server Hourly Cost 0.34
Peak power 300 W
Idle power 100 W
CPU drained power 180 W
Memory drained power 20 W
6 SIMULATION RESULTS
We start observing that the heuristic is heavily depen-
dent on the order of the virtual machines in the prob-
lem, as the basic algorithms producing the initial so-
lutions to improve upon (Next Fit, First Fit, Best Fit)
are such. These algorithms aren’t suited for multiple-
choice knapsack optimization problems, so they find
a solution considering only the lowest SLA for each
virtual machine. Also, these algorithms doesn’t offer
any possible tuning, and each one of them produces
just a single solution to the problem. We then perform
a permutation of the virtual machines in the dataset,
because these algorithms are all particularly sensitive
to the ordering (as their names suggest) while chang-
ing it doesn’t produce a new problem but only a pos-
sible different solution. For the heuristic, we have
done 20 random permutations for each initial algo-
rithm, seeing that the resulting differences in the prof-
its are quite narrow. The heuristic is quite fast, with
a computation time of about 2 seconds on a low level
desktop system.
Figure 1 shows the results when the kWh varies
from 0.1 to 1, for PUE=1.5 and C=0.34. If we look
back at table 1, we see that the lowest number of
CPUs to be allocated is 312, requiring a minimum of
341 GBs of RAM. The allocations on figure 1 results
in 383, 399 or 400 CPUs (the number is dependent
on the permutations of initial data and the specific
basic algorithm), with respectively 494, 506 or 507
GBs of RAM. The combined resources from the 32
servers are of 512 CPUs and 1024 GBs of RAM. So
the heuristic is better than a simple First/Next/Best Fit
algorithm, as it does find some improvements, but at
some point is unable to progress, and it almost finds a
plateau.
Figure 2 shows the results for different values of
kWh and PUE, for C fixed at 0.34. Clearly, increase
in kWh cost or in PUE results in less profits, and the
surface is almost regular, confirming our analysis on
50
51
52
53
54
55
56
57
58
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Profit
kWh
Figure 1: Heuristic results with PUE=1.2 and C=0.34.
0.1
0.2
0.3
0.4
0.5
1.2
1.4
1.6
1.8
2
52
54
56
58
Profit
kWh
PUE
Profit
Figure 2: Heuristic results with C=0.34.
the limits of this solution technique.
For the GA, we have considered only 600 gen-
erations for each problem instance; a single gener-
ation requires about 3 seconds of computation on a
medium level desktop system, with a code that is not
optimized for speed; as with every genetic algorithm,
these computations are massively parallelizable, so
we don’t consider the time scale as a critical factor.
The GA starts with an initial population (i.e. a set
of solutions) constructed as for the heuristic, i.e. ap-
plying the First Fit, Best Fit and Next Fit algorithms
to the associated bin packing optimization problem
after some random permutations. Then, this popu-
lation is fed to the GA, that starts its optimization
phase. By looking at the population’s average fitness,
we see how the optimization is quite steep at the be-
ginning, then it almost reaches a plateau around 300
generations. The average fitness (which is the sum of
the objective function in eq. 6 and of an evaluation
of the slackness of the proposed allocation) starts at
about 120, then increase linearly as more better solu-
tions are found and enter in the populations removing
worse ones; finally around 300 generations the local
optimum is found, and so the average fitness of the
population starts to stabilize.
Figure 3 shows the results for different values of
kWh, for a fixed value of PUE set at 1.5. Although
the curve isn’t smooth, it clearly shows a trend: when
the price of kWh increases the profit decreases. This
could be explained both by the effect of the fixed
part of costs (idle power of servers) and by the re-
duced economic convenience in allocating resources
AVIRTUALMACHINESPLACEMENTMODELFORENERGYAWARECLOUDCOMPUTING
251

75
85
95
105
115
0.1 0.4 0.8 1.2 1.6
Profit
kWh
Figure 3: Profits for different values of kWh (PUE=1.5).
for more demanding virtual machines. We see that the
GA outperforms the heuristic almost by a factor of 2.
We lack a way to show the solutions to these dif-
ferent instances in a readable way, but by analytically
looking at them we see that the allocations change
when a model parameter changes. This means, at
first, that the GA has successfully been made energy-
aware, incorporating all the energy metrics in the
search for a local optimum (which could or could not
be the global optimum, but either way is a significant
improvement over the initial solution). The rough
edges that we see could be explained considering the
general problem is composed of a linear part (energy
costs are almost linear with respect to the amount of
resources) but also of a non-linear part (allocation of
resources does not allow for fractional allocations),
and these two different parts of the model interacts
in an way that appears unintuitive. Also, we have
defined the fees as an almost linear relation of the
resources consumption, and by doing this we have
significantly reduced the GA’s ability to leverage on
prices to find a more economically convenient alloca-
tion of resources. We don’t see this for the heuristic
because it simply fails to aggressively optimize the
allocations.
7 CONCLUSIONS
We have developed a model that deals with both oper-
ational expenses and capital expenses of a cloud com-
puting system. The Cloud Service Provider has the
economic incentive to maximize its revenues. To do
so, it must take into account all the costs related to the
infrastructure provisioning and day to day operations,
with a major part of them made by electricity costs.
On the other side, the Cloud Service Customer is in-
terested in reducing the fees it has to pay for the cloud
deployment of its infrastructure, but also wants the
biggest flexibility in choosing the right size of its sys-
tems. To successfully manage and compose these two
conflicting interests, we have to deploy comprehen-
sive model of resources allocation for a cloud archi-
tecture, where we cannot consider only CPU require-
ments to define both virtual machines properties, al-
location schema and energy power consumption. The
model should allow for more detailed negotiations be-
tween the two parties, where one or the other could
offer (or ask) for different level of services, also keep-
ing in mind the capacity of the cloud architecture to
accommodate for this and the resulting different op-
erational expenses. The resulting model that we have
developedin this paper offers all of this kind of gener-
ality, and we have developed approximate algorithms
to solve it. Results show that the heuristic fails to find
a good solution, while the genetic algorithm performs
better. Also, we consider that a GA is particularly
fitted to this kind of problems, as genetic algorithms
are both easily parallelizable (and cloud computing
has vast and scalable amount of resources) and evolu-
tionary (and cloud computing architectures offers the
ability to change the current allocation of virtual ma-
chines via live migration of them). A first analysis
of the model shows that the non-linear part (resources
allocation) interacts in complex ways with the linear
part (energy model), suggesting that more researches
and characterizations of cloud architectures should be
investigated to further analyze this problem which is
of capital importance for the economics of green and
cloud computing.
ACKNOWLEDGEMENTS
We would like to thank Emiliano Casalicchio for his
suggestions and support during the development of
this work. Ancitel SpA generously provided a travel
grant.
REFERENCES
Beloglazov, A. and Buyya, R. (2010). Energy efficient allo-
cation of virtual machines in cloud data centers.
Campegiani, P. (2009). A genetic algorithm to solve the vir-
tual machines resources allocation problem in multi-
tier distributed systems. In 2nd International Work-
shop on Virtualization Performance: Analysis, Char-
acterization and Tools (VPACT'09).
Campegiani, P. and LoPresti, F. (2009). A general model
for virtual machines resources allocation in multi-tier
distributed systems. In 5th International Conference
on Autonomic and Autonomous Systems (ICAS '09).
IARIA.
Cardosa, M., Korupolu, M. R., and Singh, A. (2009).
Shares and utilities based power consolidation in vir-
tualized server environments. In IFIP/IEEE Interna-
SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems
252

tional Symposium in Integrated Network Management
(IM '09). IEEE.
Chang, F., Ren, J., and Viswanathan, R. (2010). Optimal re-
source allocation in clouds. In 3rd IEEE International
Conference on Cloud Computing.
Economou, D., S. Rivoire, C. K., and Ranganatham, P.
(2006). Full-system power analysis and modeling
for server environments. In Workshop on Modeling
Benchmarking and Simulation (MOBS).
Gandhi, A., Harchol-Balter, M., Das, R., and Lefurgy, C.
(2009). Optimal power allocation in server farms. In
SIGMETRICS/Performance '09.
Lu, X. and Gu, Z. (2011). A load-adaptive cloud resource
scheduling algorithm model based on ant colony al-
gorithm. In IEEE Cloud Computing and Intelligent
Systems.
Mazzucco, M. and Dumas, M. (2011). Reserved or on-
demand instances? a revenue maximization model for
cloud providers. In IEEE 4th International Confer-
ence on Cloud Computing.
McCullogh, J., Agarwal, Y., and Chandrashekar, J. (2010).
Evaluating the effectiveness of model-based power
characterization. In USENIX Annual Technical Con-
ference.
Rivoire, S., Ranganathan, P., and Kozyrakis, C. (2008). A
comparison of high-level full-system power models.
In Conference on Power aware computing and sys-
tems (HOTPOWER'08). USENIX.
Singh, K., Bhadauria, M., and McKee, S. A. (2009). Real
time power estimation and thread scheduling via per-
formance counters. ACM SIGARCH Computer Archi-
tecture News, 37(2):46–55.
Srikanthaiah, S., Kansal, A., and Zhao, F. (2008). Energy
aware consolidatin for cloud computing. In Confer-
ence on Power aware computing and systems (HOT-
POWER'08). USENIX.
Urgaonkar, R., Kozat, U. C., Igarashi, K., and Neely, M. J.
(2010). Dynamic resource allocation and power man-
agement in virtualized data centers. In IEEE Network
Operations and Management Symposium (NOMS'10).
AVIRTUALMACHINESPLACEMENTMODELFORENERGYAWARECLOUDCOMPUTING
253
