SMART INTEGRATION OF ELECTRIC VEHICLES IN AN ENERGY

COMMUNITY

Ebisa Negeri and Nico Baken

Delft University of Technology, Delft, The Netherlands

Keywords:

Smart Grid, Load Balancing, Distributed Generation, Electric Vehicle.

Abstract:

With increasing penetrations of renewable distributed generations (DGs) and electriﬁed vehicles (EVs), the

volatility of the renewable sources and the huge load of the EVs induce tremendous challenges for the power

grid. The two technologies also have considerable synergetic potential to alleviate these challenges if they are

intelligently coordinated. The aim of this paper is to investigate how the (dis)charging of EVs could be intelli-

gently coordinated with the production of the local DGs to reduce the peak load on the power grid. We consider

a neighborhood energy community that is composed of prosumer households. Three EV (dis)charging scenar-

ios are compared: the dumb strategy where all EVs are charged for the next commute as soon as they return

from the previous commute, the centralized (dis)charging strategy where the EVs are managed by a central-

ized scheduling unit, and the distributed (dis)charging strategy where the households autonomously schedule

their EVs while coordination is achieved through providing dynamic pricing based incentives. Our simulation

results show that the distributed and centralized charging strategies can reduce the peak load up to 44.9%

and 75.1%, respectively, compared to the dumb charging strategy. Moreover, the relative performnce of the

algorithms with respect to environmental values.

1 INTRODUCTION

As distributed generations (DGs) are increasingly

penetrating into the lower parts of the power grid,

the end consumers, such as households, are evolv-

ing from passive consumers to active prosumers. Ac-

cording to the EU parliament, all buildings built af-

ter 2019 will have to produce their own energy on

site

. Production of own power on site leads to for-

mation of energy communities (Melo and Heinrich,

2011) that could autonomously manage their own re-

sources and locally exchange power with themselves.

On the other hand, the increasing trend in electriﬁca-

tion of the transportation sector is expected to bring

about massive presence of electriﬁed vehicles (EVs)

in the near future.

Since most of the DGs have intermittent electric-

ity production patterns, their large composition might

lead to unacceptable volatile proﬁles that disrupt the

grid stability, power quality, and infrastructure con-

straints. Likewise, presence of an EV doubles the

average power demand of a household (Ipakchi and

European Parliament, “All New Buildings to be Zero

Energy from 2019,” Committee on Industry, Research and

Energy, Brussels 2009.

Albuyeh, 2009), thus its massive presence imposes

very large load on the grid. On the other hand, the

EVs provide considerable ﬂexibility that could be ex-

ploited to minimize these challenges. Given that EVs

are idle 95% of the time, more than 90% of all ve-

hicles are parked at any given point in time with

more than 25% of them parked at home (Fluhr et al.,

2010), their charging could be conveniently shifted to

periods of surplus local production. Moreover, the

vehicle-to-grid (V2G) technology gives the possibil-

ity of discharging from the EV back to the grid dur-

ing peak demand periods. Thus, by coordinating the

(dis)charging of the EVs with the local production of

DGs, one can reduce the load of the EVs on the grid,

shield the intermittence of the DGs from the grid, and

reduce the carbon footprint of the EVs. Accordingly,

EVs and DGs seem to form a natural combination.

Although there are a few works in the litera-

ture that consider the synergy between the renewable

sources and the EVs ((Markel et al., 2009), (Lund and

Kempton, 2008), (Verzijlbergh et al., 2011)), they fo-

cus on a high-level study of the coordination of ﬂeets

of EVs and large scale renewable sources on large ge-

ographical regions, without considering the local ef-

fects on the grid constraints and the driving behaviors

of the users of the EVs. In this paper, we endeavor

Negeri E. and Baken N..

SMART INTEGRATION OF ELECTRIC VEHICLES IN AN ENERGY COMMUNITY.

DOI: 10.5220/0003952400250032

In Proceedings of the 1st International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2012), pages 25-32

ISBN: 978-989-8565-09-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

to ﬁll this gap by investigating how the (dis)charging

of EVs can be efﬁciently coordinated with the local

generation of power from DGs to minimize the peak

load while considering the local grid constraints and

the driving behaviors. We consider a model futuris-

tic residential neighborhoodenergy community that is

described in the next section. We present three differ-

ent EV (dis)charging strategies: a reference dull strat-

egy, a centralized strategy and a distributed strategy.

The relative gain of these strategies are compared.

The remainder of this paper is organized as fol-

lows. The architecture of the energy community is

presented in Section 2. After describing the system

model in Section 3, we go on to present the three co-

ordination strategies in Section 4. In Section 5, we

present and discuss the simulation results, then we ﬁ-

nalize the paper with the concluding remarks in Sec-

tion 6.

2 THE NEIGHBORHOOD

ENERGY COMMUNITY

In our work, we consider a neighborhood energycom-

munity that is connected to a single medium-voltage

to low-voltage (MV/LV) transformer. A simpliﬁed di-

agram of such a neighborhood is shown in Figure 1.

The energy community comprises of prosumer house-

holds. The prosumer households can autonomously

manage their own load proﬁle. Each household can

generate, store, import or export power. Power can be

exchanged between the prosumer households in the

community as well as between the energy community

and the MV grid in either direction.

A multi-agent based control is used to coordinate

the households. Each household has a household-

agent that coordinates its resources to optimize

the household consumption. A community-agent

watches over the overall load distribution of the com-

munity and coordinates the household-agents accord-

ingly. In addition, the community-agent manages the

energy exchange with the rest of the grid.

The energy community is assumed to have a smart

grid infrastructure in place. Each agent in the en-

ergy community has an intelligent device that can

exchange information with the other agents across a

communication infrastructure, and process the infor-

mation to make decisions.

3 THE SYSTEM MODEL

In this section, the mathematical model of the energy

Figure 1: A schematic diagram of a neighborhood energy

community.

community is presented. We consider a scheduling

time period τ (24h) that is divided into time steps, i.e.

τ = {1, 2, ..., T}, that have equal duration of ∆ time

units (15 min.).

3.1 Electric Vehicle

To characterize each EV, the parameters of its bat-

tery are important. The battery parameters of interest

for this work are the following: the maximum energy

storage capacity (Φ in kWh), the cycle efﬁciency (η

in %), the maximum depth of safe discharging to pro-

long battery life (δ

in %), and the maximum level of

safe charging to prolong battery life (δ

dch

%). Assum-

ing a symmetric cycle efﬁciency, we denote the stor-

age charging efﬁciency and discharging efﬁciency by

and η

dch

, respectively, where η

= η

dch

√

η.

The state of charge (SOC) of the battery at time step i

is denoted by ψ

. The amount of electrical power con-

sumed to charge the battery of the EV, and the amount

of electrical power supplied from the battery upon dis-

charging (V2G) in time step i are denoted by X

and

, respectively. After the EV commutes a distance

of l km, the state of charge of its battery drops by an

amount l×ω, where ω is the average amount of stored

battery energy the EV consumes per unit km travelled

(in kWh/km).

In this work, we focus on the impact of EVs on the

power grid of a residential energy community. Thus,

we consider only the case where the EVs are charged

and discharged (V2G) within the energy community

either at home or at a charging station within the com-

munity. We denote the periods of time the EV stays

within its community and away by τ

and τ

−h

, respec-

tively. The usage of EV is subject to the constraints

listed in Eq.1-8. Eq.1 states that the SOC at the end

of a time step j can be obtained from the SOC at the

end of the previous time step i by adding the net rise

in the SOC in time step j. The net rise in the SOC re-

sults from the injected energy via charging (∆η

the supplied energy via discharging (∆η

dch

) and the

SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems

battery energy used in commuting (π

). ∆ is em-

ployed here to convert power into energy. Constraints

2 and 3 represent the maximum and minimum bound-

aries, respectively, on the SOC for safety of the bat-

tery. Constraint 4 says that the battery of the EV can-

not be charging and discharging at the same time. On

the other hand, constraints 6 and 5 enforce the maxi-

mum and minimum charging and discharging rates of

the battery, respectively, where υ

and υ

dch

denote

the maximum charging and discharging rates, respec-

tively, of the charger. Constraint 7 reﬂects that we are

limiting the (dis)charging of the EVs only to the peri-

ods when they are within their community. Whenever

an EV begins to commute a distance of l km, its bat-

tery level should be large enough to commute the dis-

tance, and yet not fall below the minimum safe SOC

after commuting (constraint 8).

The deriving behavior of the EV user is derived

from a mobility data, as will be described in section

= ψ

+ ∆(η

−η

dch

) −π

, ∀i, j ∈ τ (1)

≤ δ

Φ, ∀i ∈ τ (2)

≥ δ

dch

Φ, ∀i ∈ τ (3)

= 0 or Y

= 0, ∀i ∈ τ (4)

0 ≤ Y

≤ υ

dch

, ∀i ∈τ (5)

0 ≤ X

≤ υ

, ∀i ∈ τ (6)

= 0, ∀i ∈ τ

−h

(7)

≥ δ

dch

Φ+ lw, commute of l km begins at i(8)

3.2 Household Demand and Production

The accumulated power demand of all the appliances

of the household in time step i is denoted by D

This demand does not include the demand of the EV

owned by the household, because the EV is modeled

separately. We designate the total power production

of all the DGs owned by the household in time step i

by P

. In this work, we assume that forecasts of D and

P are available for the entire scheduling period. The

net demand of a household in time step i, denoted by

, is deﬁned as the difference between the demand

(appliances and EV) and the production of the house-

hold (Eq.9). R

is upper bounded by the power capac-

ity of the line connecting the household to the grid,

(Eq.10).

= [D

+ (X

−Y

)] −P

, ∀i ∈ τ (9)

≤ L

, ∀i ∈ τ (10)

3.3 Transformer

The net power ﬂow through the transformer, that con-

nects the community to the rest of the grid, at any

time step i is equal to the net demand of the commu-

nity, P

net

given in Eq.11, and is generally constrained

by the threshold capacity of the transformer (P

), as

shown in Eq.12. In our case, we loosen the constraint

in Eq.12 and try to minimize the peak load using dif-

ferent charging strategies. Observing the resulting

peak load helps to suggest the optimal value of the

transformer rating to be installed to support the load

proﬁle in the energy community under consideration.

net

= (

∑

all houses

), ∀i ∈τ (11)

net

≤ P

, ∀i ∈ τ (12)

4 THE CHARGING STRATEGIES

In this section, we present three EV charging strate-

gies, namely, the dull strategy, the centralized strat-

egy, and the distributed strategy.

4.1 The Dull Strategy

This strategy represents a reference scenario where

the EVs are charged for their next commute as soon

as they return to the community from their previous

commute. The EVs are charged up to the target bat-

tery level without interruption at the maximum pos-

sible rate. Apparently, this strategy does not possess

any intelligence, hence the name dumb.

4.2 The Centralized Strategy

The centralized charging strategy assumes that the en-

ergy community is composed of prosumers that coop-

erate with each other to achieve communal goals. In

this case, (dis)charging of the EVs are scheduled of-

ﬂine in a centralized way by an intelligent scheduling

unit (ISU) that could be located at the community-

agent. As opposed to the dumb strategy, this strat-

egy allows charging of the EVs with variable charg-

ing rates and with possible interruptions. This strat-

egy ﬁnds optimal schedules as a solution to a linear

programming problem that is shown in Eq.13, where

peak denotes the peak value of the net demand of the

energy community (P

net

). Apparently, this strategy

aims at aligning the EVs with the local production to

minimize the peak load on the transformer.

minimize peak (13)

subject to Eq. 1-12

SMARTINTEGRATIONOFELECTRICVEHICLESINANENERGYCOMMUNITY

4.3 The Distributed Strategy

This strategy is based on the assumption that each

household tends to selﬁshly maximize its own ben-

eﬁts. The EVs are autonomously scheduled by their

respective owners. Thus, a coordination mechanism

is required to maximize utilization of the locally

generated power. Our coordination mechanism in-

volves a local electronic energy market (Kok et al.,

2005) within the community where the autonomous

households trade electricity with each other, whereby

the autonomy of the energy community allows the

community-agent to propose local price-vectors to

achieve desirable communal goals. The community-

agent provides incentives based on a novel dynamic

pricing model that aims at motivating the community

members to shift their demands to lower the peak load

on the transformer.

4.3.1 The Cost

To handle the power import and export of each house-

hold, the dynamic pricing model has two components

for each time step i: the import tariff (γ

) and the

export tariff (γ

). The cost of the household is mod-

eled in Equation 14 for each time step i, where the

terms (γ

∗R

) and (γ

∗R

) represent the monetary

cost and beneﬁt, respectively, incurred due to the net

demand of the household.



∗R

, if R

≥ 0

∗R

, if R

< 0

(14)

4.3.2 The Household Optimization

Each household schedules its EVs to minimize its cost

by solving a linear household optimization problem

that is shown in Equation 15.

minimize

∑

∀i∈τ

(15)

subject to Equations 1-9, 14.

4.3.3 The Dynamic Pricing Model

In order to ﬂatten the overall load distribution of the

neighborhood, the community-agent provides each

household with an incentive that is based on a dy-

namic pricing model. In our dynamic pricing model,

the community-agent proposes a price vector, then

each household-agent schedules the storage unit of

that household and replies with the corresponding

scheduled demand of the household. Based on the

response of all the households, the community-agent

adjusts the price vector using an intelligent learning

mechanism. This is repeated iteratively to obtain a

ﬂattened proﬁle.

In the proposed pricing model, the cost of a unit

power varies from one time step to another depending

on the net demand of the neighborhood energy com-

munity (P

net

). Our pricing model aims at encouraging

the households to shift their scheduled demands away

from the peak periods of the overall scheduled de-

mand of the neighborhood. The optimal tariff for each

time step is determined iteratively. At the (j + 1)

it-

eration cycle, the tariff for the i

time step is obtained

by adjusting the corresponding tariff in the previous

iteration cycle j using an incremental factor (γ×ξ

j,i

j+1,i

= θ

j,i

(1 + γ×ξ

j,i

) (16)

The incremental factor is composed of two terms:

the learning factor (γ) and the deviation factor (ξ

j,i

The learning factor is a constant (0 < γ ≤1) that deter-

mines to which extent the deviation factor overrides

the old price vector. The deviation factor captures the

variation of P

net

from its average value. Let P

net

the net demand of the energy community in the i

time step for the j

iteration cycle. Let mean be the

average of the net demand:

mean =

∑

i=1

net

The deviation factor, ξ

j,i

, is given by

j,i

= sign×

net

−mean)

∑

i=1

net

−mean)

(17)

where the sign determines whether the incremental

value should be positive or negative. If P

net

> mean,

then we add a positive incremental value to the tariff

to reduce consumption in this time step: sign = 1. If

net

< mean, then we substract an incremental value

from the tariff to increase consumption in this time

step: sign = −1. Clearly, ξ

j,i

reﬂects the effect of

the offset of the demand from the mean value on the

price vector. The pricing model increases tariff on

the time steps where the overall scheduled demand of

the neighborhood community (P

net

) is above the aver-

age, and reduces tariff when P

net

is below the average,

thereby providing incentives to the households to ﬂat-

ten the overall scheduled neighborhood demand.

The power feed-in tariffs are obtained by sub-

stracting the transport part of the import tariffs as sug-

gested in (Houwing et al., 2011). Consequently,

= θ

−θ

, ∀j ∈τ (18)

where θ

is the transport part of the import tariff θ

4.3.4 The Distributed Algorithm

Our proposed distributed algorithm comprises of two

types of algorithms. The ﬁrst type of algorithm (Al-

gorithm 1) is implemented at the community-agent

SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems

while the other (Algorithm 2) is implemented at each

household-agent. These algorithms iteratively solve

the household optimization problems by exchanging

information. The iteration cycles continue for a ﬁxed

number of iterations maxIteration, while searching

for an optimal price vector that yields the smallest

peak value for the overall net demand of the neigh-

borhood energy community (P

net

The block diagram describing the execution of the

algorithms is shown in Figure 2. At each iteration

step, the community-agent sends the recent tariff in-

formation to each household-agent. Then, it receives

the scheduled demand of the households subject to

the corresponding tariff. Afterwards, it computes the

tariffs for the next iteration cycle based on the overall

scheduled demand of the community (P

net

). On the

other hand, each household-agent in each iteration cy-

cle solves its household optimization problem using

the tariff information received from the community-

agent. It then sends the updated scheduled demand of

the household (R) to the community-agent.

Figure 2: Block diagram of the distributed charging strat-

egy.

Algorithm 1: Executed at neighborhood agent.

1: Initialize θ and λ, counter = 0

2: repeat

3: send θ and λ to each household

4: Receive R from each household

5: Update P

net

using Eq. 11

6: Update θ and λ using using Eq.16 and Eq.18.

7: increment counter by 1

8: until counter ≤ maxIteration

9: send a “DONE” message to each household

Algorithm 2: Executed at each household.

1: repeat

2: receive θ and λ from the neighborhood agent

3: solve the household optimization problem in Eq.15

4: update R according to the solution

5: send R to the neighborhood agent

6: until a “DONE” message is received from the neigh-

borhood agent

Solving the optimization problems is initiated at

the community-agent (Algorithm 1). The algorithm

starts by initializing the tariffs (θ and λ) to ﬂat price

vectors and the iteration cycle counter (counter) to

zero in line 1. In each iteration cycle, lines 3-7 are

executed. In line 3, the recent tariff information is

sent to each household-agent which will be used by

the household-agent to solve the household optimiza-

tion problem in the current iteration cycle. It then re-

ceives from each household-agent its scheduled de-

mand (R) resulting from the solution of the house-

hold optimization problem in the current iteration cy-

cle (line 4). After computing the overall net demand

of the neighborhood P

net

in line 5, the tariffs used in

the next iteration cycle are updated accordingly (line

6). The iteration continues until the iteration count is

equal to maxIteration. The algorithm ﬁnalizes the op-

timization process by sending the “DONE” message

to all the household-agents (line 9). The optimal tariff

is chosen by selecting tariff vectors that yielded the

lowest peak value of P

net

The algorithm at each household-agent (2) itera-

tively solves the household optimization problem. In

each iteration cycle, the algorithm receives the up-

to-date tariff information from the community-agent

(line 2), solves its optimization problem using the new

tariffs (line 3), updates the scheduled demand of the

household according to the solution (line 4) and sends

it back to the neighborhood-agent (line 5). The itera-

tion continues until a “DONE” message is received.

5 SIMULATION

5.1 Simulation Data

The data for the demand and electricity production

of a household are acquired from Alliander

. The

DGs of the household are a PV panel and a micro-

CHP. The data were obtained by ﬁeld measurements

that were taken every 15 minutes for a duration of 24

hours using smart meters installed at the households.

The micro-CHP generation is constant (1 kW) over

each period of operation, and the data speciﬁes the

start time and end time of each period of its opera-

tion. To make alternative proﬁles for each household,

we randomized the values according to a normal dis-

tribution around the measured values. A sample of the

daily production and demand proﬁle of a household is

shown in Fig. 3.

The driving behavior of the EV users are con-

structed based on the data from the 2009 mobility re-

Alliander is the largest electricity distribution network

operator company in the Netherlands owning 40% of the

distribution networks.

SMARTINTEGRATIONOFELECTRICVEHICLESINANENERGYCOMMUNITY

10 20 30 40 50 60 70 80 90

0.2

0.4

0.6

0.8

1.2

Time Steps

Power (kW)

demand

micro−CHP

PV panel

Figure 3: A sample household demand and production pro-

ﬁles.

10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

distance (km)

cummulative probability

Figure 4: Distribution of the distance travelled per day per

car driver.

search of the Netherlands (MON, 2009). Fig. 4 shows

the distribution of the distance traveled per car driver

per day as extracted from the data. The commute

distances used in the simulations are generated us-

ing a function with exponential distribution that best

ﬁts the data. For each commute, the departure and

arrival time from/at home are generated using Gaus-

sian functions that best approximate the data obtained

from (MON, 2009).

In our simulations, we involve three types of elec-

tric cars whose technical speciﬁcations and market

share are speciﬁed in (Knapen et al., 2011), as pre-

sented in Table 1. The composition of the EVs in

the energy community is in line with the market share

values in Table 1. The values of the cycle efﬁciency

of the batteries, the safe charging level and the safe

discharging level are adopted from (Lombardi et al.,

2009), with the values η = 95%, δ

= 90%, and

dch

= 30%. We conducted our simulations with com-

munity size, N = 50 households, with a conservative

assumption that each household owns one EV. The

average number of cars per household is about 1.6

according to (MON, 2009), thus our assumption of

one EV per household represents roughly 62% pene-

tration of the EVs. We assume that each household

is connected to the grid with a standard connection of

230V and 40A (the case in The Netherlands) resulting

in a line limit of L

= 9.2 kW.

Table 1: Technical characteristics for vehicles in speciﬁc

categories, and their market share (Knapen et al., 2011).

EV category small medium large

Market share 0.496 0.364 0.140

Φ [kWh] 10 20 35

Range [km] 100 130 180

ω [kWh/km] 0.1 0.15 0.19

5.2 Simulation Results

We present different cases that compose our simu-

lation scenarios. We consider two types of charg-

ers: slow charger (υ

=3.3 KVA) and fast charger

(υ

=7.2 kVA), that are compatible with the Flem-

ish grid (Knapen et al., 2011). Moreover, we con-

sider two cases: chargingwith V2G and without V2G.

While the ﬁrst case allows feeding from the EV bat-

tery back to the grid, the later does not allow it. We as-

sume that the rate of V2G discharging is constrained

by the same threshold value, i.e., υ

dch

= υ

. In ad-

dition, two cases are considered concerning the target

battery level at the start time of each commute. In the

ﬁrst case we assume that the target battery level is just

sufﬁcient to support the commute (Eq. 8), whereas in

the second case the target battery level is the maxi-

mum safe charging level of the battery (90% of Φ).

Combining these cases, we present eight simulation

scenarios to compare the performance of our charg-

ing strategies.

slow, with V2G slow, w/o V2G fast, with V2G fast, w/o V2G

community peak demand (kW)

dumb

distributed

centralized

24.6

14.6

14.7

38.8

14.2

Figure 5: Comparison of the algorithms based on the peak

demand of the community (target battery level is commute

energy).

For the case when the target battery level at the

start of each commute is the energy required for the

commute, the relative performance of the charging

strategies under four different scenarios are presented

in Fig.5. The numbers on the top of the bars represent-

ing the distributed and the centralized charging strate-

gies denote the percentage reduction in the peak load

as compared to the dumb charging strategy. As can

be observed from the ﬁgure, the distributed charging

SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems

slow, with V2G slow, w/o V2G fast, with V2G fast, w/o V2G

100

120

140

160

community peak demand (kW)

dumb

distributed

centralized

26.6

59.7

11.8

59.7

44.9

75.1

74.2

Figure 6: Comparison of the charging strategies based on

the peak demand of the community (target battery level is

90% of the battery capacity).

strategy yields a reduction in the peak load by around

14% in all the four scenarios, which averageto 14.4%.

On the other hand, the centralized charging strategy

reduces the peak by as large as 65%, with average im-

provement of 38.1%.

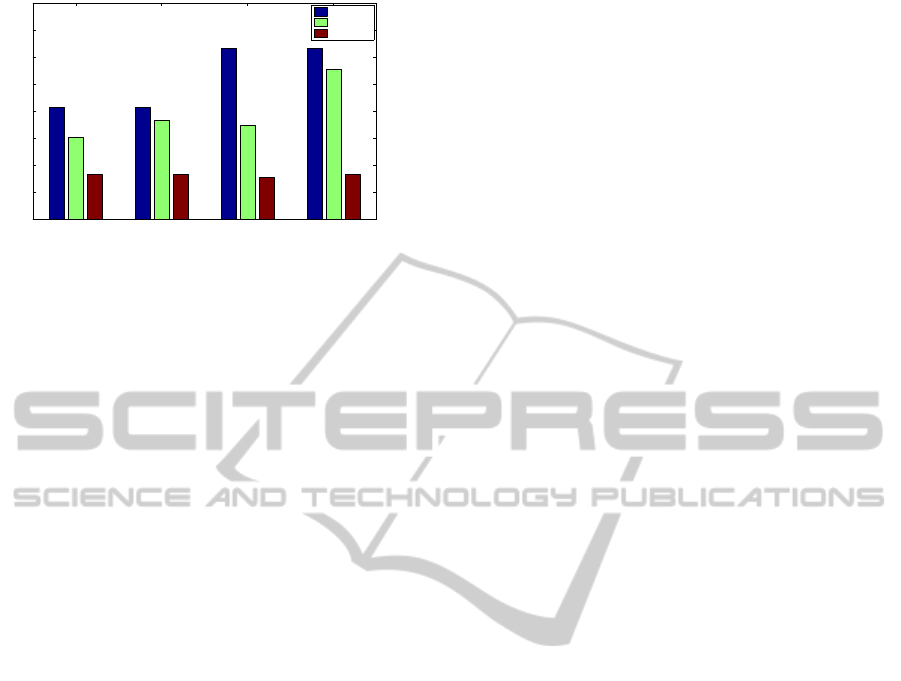
Figure 6 depicts the relative performance of the

charging strategies when the target battery level at the

start of each commute is 90% of the battery capac-

ity. In this scenario, the distributed charging strategy

achieves an average peak reduction of 23.9%, where

its largest reduction is as high as 44.9%. Whereas

the centralized charging strategy obtains 67.2%, with

75.1% largest improvement.

All the simulation results reveal that the dumb

charging strategy results in large peak demands which

arise from the simultaneous charging of EVs right af-

ter they arrive at home. In the contrary, the central-

ized charging strategy has effectively revealed the po-

tential of the synergy between the EVs and the lo-

cal production to reduce the peak load by exploiting

the ﬂexibility of the EVs. However, the centralized

charging strategy represents a situation where all the

households are cooperative to reduce the peak load

and all the EVs are managed by a centralized unit,

which might contradict the tendency of the house-

holds to autonomously manage their own EVs. On

the other hand, the distributed charging strategy de-

livers 11% to 44.9% reduction in peak demand over

the dumb charging strategy while respecting the au-

tonomy of the households to manage their own EVs.

The strength of the distributed strategy lies in the dy-

namic pricing model that is used as incentive to co-

ordinate the autonomous households that tend to self-

ishly minimize their cost. These improvements are

vital because they reduce the load on the transformer

connecting the energy community with the remain-

ing power grid. The reduction in the peak values has

the advantage of increasing the lifetime of the trans-

former as well as minimizing the need for installing

large capacity transformer.

6 CONCLUSIONS

In an energy community composed of prosumer

households that own EV, the aggregate load proﬁle

might become highly volatile due to the intermittence

of the distributed generations as well the load of the

EVs, which could lead to a large peak load that might

exceed the capacity of the transformer. We have pro-

posed a centralized and a distributed EV charging

strategies that try to minimize the peak load in such

scenario by exploiting the synergy between the lo-

cal distributed generations and the ﬂexibility of the

EVs. Our centralized charging strategy schedules the

(dis)charging of the EVs at a centralized unit assum-

ing that all the prosumers in the energy community

cooperate with each other to minimize the peak de-

mand. Our distributed charging strategy, however,

assumes that the prosumer households autonomously

manage their EVs and tend to selﬁshly minimize their

cost. Our distributed strategy coordinates the house-

holds to minimize the peak demand by providing in-

centives based on our novel dynamic pricing model.

In addition to presenting a detailed model of the sys-

tem taking into consideration the local constraints, we

have derived the driving behaviors of the EV users

from a realistic mobility data. Based on our simula-

tion results, we have shown that our centralized and

distributed charging strategies can reduce the peak by

as large as 75.1% and 44.9%, respectively, compared

to a reference dumb charging strategy. Therefore, our

proposed strategies can help to reduce the load on the

transformer connecting the energy community to the

rest of the grid, and also minimizes the need for up-

grading the capacity of the transformer.

REFERENCES

Fluhr, J., Ahlert, K., and Weinhardt, C. (2010). A stochastic

model for simulating the availability of electric vehi-

cles for services to the power grid. In 43rd HICSS,

2010, pages 1–10. IEEE.

Houwing, M., Negenborn, R., and De Schutter, B. (2011).

Demand response with micro-chp systems. Proceed-

ings of the IEEE, 99(1):200–213.

Ipakchi, A. and Albuyeh, F. (2009). Grid of the future.

Power and Energy Magazine, IEEE, 7(2):52–62.

Knapen, L., Kochan, B., Bellemans, T., Janssens, D., and

Wets, G. (2011). Activity based models for coun-

trywide electric vehicle power demand calculation.

SGMS.

Kok, J., Warmer, C., and Kamphuis, I. (2005). Power-

matcher: multiagent control in the electricity infras-

tructure. In Proceedings of the fourth international

joint conference on Autonomous agents and multia-

gent systems, pages 75–82. ACM.

SMARTINTEGRATIONOFELECTRICVEHICLESINANENERGYCOMMUNITY

Lombardi, P., Vasquez, P., and Styczynski, Z. (2009). Plug-

in electric vehicles as storage devices within an au-

tonomous power system. optimization issue. In Pow-

erTech, 2009 IEEE Bucharest, pages 1–7. IEEE.

Lund, H. and Kempton, W. (2008). Integration of renew-

able energy into the transport and electricity sectors

through v2g. Energy Policy, 36(9):3578–3587.

Markel, T., Kuss, M., and Denholm, P. (2009). Communi-

cation and control of electric drive vehicles supporting

renewables. In VPPC’09. IEEE, pages 27–34. IEEE.

Melo, H. and Heinrich, C. (2011). Energy balance in a re-

newable energy community. IEEE EEEIC.

MON (2009). Mobility research of the netherlands 2009

(mobilitietsonderzoek nederland (mon) 2009). avail-

able: http://rijkswaterstaat.nl/.

Verzijlbergh, R., Ilic, M., and Lukszo, Z. (2011). The role

of electric vehicles on a green island. In NAPS, 2011,

pages 1–7. IEEE.

SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems