VOLTAGE CONTROL ISSUES IN LOW VOLTAGE NETWORKS

WITH MICROGENERATION

Rui Castro, M. E. Almeida, Célia Jesus, Pedro M. S. Carvalho and Luís A. M. Ferreira

Centre for Innovation in Electrical and Energy Engineering (Cie

), IST – Technical University of Lisbon, Lisbon, Portugal

Keywords: Voltage Control, Microgeneration, Transformer Tap Changer, Unbalanced Load Flow.

Abstract: In the framework of the so-called microgeneration, small photovoltaic units are being installed in the roofs

of the buildings and connected to the low-voltage distribution networks. This is posing some new challenges

to the distribution network operators. On one hand, the off-service regulation of the transformer taps must

comply with a hard twofold objective: to mitigate the undervoltages during peak load periods and to

mitigate voltage rise during peak generation periods. On the other hand, the voltage profile is almost

insensitive to microgeneration injected reactive power, which forces control to actuate on active power with

the consequent impact on energy produced and also on network security. These two aspects of the problem

are addressed in this paper with help from an illustrative test network, on which several case-studies have

been built to highlight the main voltage control problems and to test different strategies to overcome such

problems.

1 INTRODUCTION

Recently, governments are encouraging the

installation of small Photovoltaic (PV) units (usually

in the roofs of the buildings), typically sized in the

range of some kW and connected to the Low

Voltage (LV) distribution network, in the framework

of the so-called microgeneration (µG). This is a way

of indirectly reduce the net load as seen from the

electrical system, because these generation units can

produce locally part of the energy consumed by the

system.

µG consists of a combination of generation

sources, usually renewable, that interface with the

LV distribution network through fast acting power

electronics. LV networks have been originally

designed to feed loads, so the introduction of

generation sources is a quite innovative aspect that

can significantly impact the flow of power and

voltage conditions.

PVs will produce electrical energy during

daylight, a period in which the load as seen from the

distribution transformer is expected to be quite low

in domestic areas. As a consequence, the power that

flows to the loads will be reduced or even be

reversed, which may cause the bus voltages to rise.

This will require some countermeasures to be

undertaken. Traditionally, this issue is dealt with by

an appropriate reactive power control. This can be

locally performed by the inverters of the PV, which

hold power factor regulation capabilities. However,

reactive power control is very ineffective in LV

networks due to the low inductive component of the

LV lines/cables. Therefore, the alternative is to

reduce the active power injected by the PVs into the

network. To cope with this purpose, the PVs must be

able to receive commands specifying the maximum

power generation level, when the voltage is out of its

range. The control of µG induced overvoltages is to

be dealt with in the scope of this paper.

Another issue related to the penetration of µG in

the LV networks concerns the tap setpoint of the

MV/LV transformer. Usually, MV/LV transformers

do not have automatic on-load tap-changing

capabilities. Instead, a fixed tap is selected with the

transformer off service. Until now, this tap has been

chosen so that the voltage along the entire feeder is

above the lower limit at peak-load hours (off-peak

generation hours). However, with embedded µG, the

chosen tap must also guarantee that the voltage

along the feeder is under the upper limit at off-peak

load hours (peak generation hours). This twofold

objective can be hard to achieve. Furthermore, it is

expected that the transformer tap changes impact

differently on voltage profile depending on the

Castro R., Almeida M., Jesus C., M. S. Carvalho P. and A. M. Ferreira L..

VOLTAGE CONTROL ISSUES IN LOW VOLTAGE NETWORKS WITH MICROGENERATION.

DOI: 10.5220/0003952700790084

In Proceedings of the 1st International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2012), pages 79-84

ISBN: 978-989-8565-09-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

elasticity of the loads and on the existence of

connected µG. The topic related to the impact of

MV/LV transformer tap changes is also addressed in

the paper.

The paper has been organized in case studies

based on the same test network. Case-studies have

been built with the aim of illustrating voltage control

problems in LV networks with µG and the

effectiveness of the proposed solutions to those

problems.

2 NETWORK MODEL

As LV networks are close to end-consumers, load

unbalance can be significant. Most small consumers

are single-phase consumers and therefore return

neutral currents can be high.

Sometimes neutral currents are even higher than

phase currents (Chen, 2001). Neutral currents

depend on the neutral earthling system in use, which

changes from utility to utility and from country to

country (Meliopoulos, 1998).

Several neutral earthling options are available.

These are usually designated by TN, TT and IT

earthing systems. The TN basic system is commonly

used in Europe and is characterized by the

transformers' neutral being earthed and the electrical

load frames being connected to the neutral.

Usually, for TN earthing systems, the earthing

impedance of the load frames grounding is high

enough to consider that all neutral current flows

back to the transformer, i.e., that the current through

the load earthing impedances is negligible during

normal operation. In such case, the system can be

well represented by a four-wire circuit (3-phases and

neutral) instead of a five-wire one (Chen, 2001);

(Ciric, 2003).

There is a scarce knowledge of the behaviour of

the LV distribution network in presence of

concurrent unbalanced generation and loads

(Chindriş, 2007); (Carvalho, 2008); (Thomson,

2007). The multidimensional stochastic dependence

structure of the joint behaviour of the generation and

load can be very complex to model. In this paper, we

assess the behaviour of unbalanced LV networks for

fixed load/generation profiles and variable load-to-

voltage elasticity with the so called three-phase,

four-wire, unbalanced power flow (Monfared,

2006); Ciric, 2003); (Teng, 2002).

3 MITIGATION OF INDUCED

OVERVOLTAGES WITH

POWER CONTROL

A small test network is used to get insight into the

voltage control problems caused by the injection of

µG into the radial LV networks. The test network is

a 5 bus network as depicted in Figure 1.

Figure 1: One-line diagram of the test network.

An unbalanced load flow study is carried out in

the following conditions: (i) the four cables are

equal with R/X = 10; (ii) the voltage in bus 1 is

considered constant and equal to 1.05 pu; (iii) the

loads were modelled as “constant current” (elasticity

equal to 1); (iv) the operating point is unbalanced,

the load complex power being presented in Table 1

(active power negative values correspond to µG).

Table 1: Unbalanced load profile, S

RST

, for the 5 bus test

network.

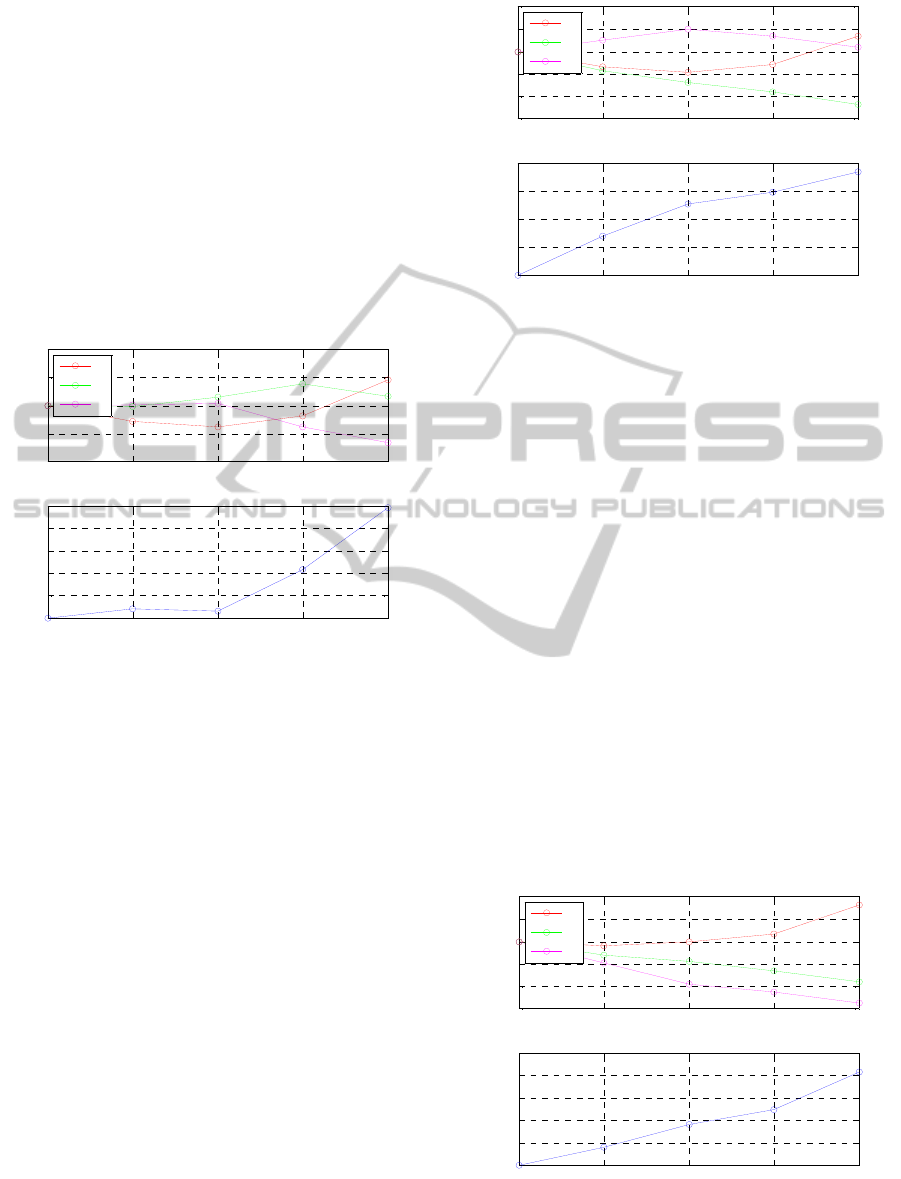
3.1 Base-case

The base-case load-flow results are presented in

Figure 2.

Figure 2: Voltage at the three phases (R, S, T) and at the

neutral for the base case.

From Figure 2 one can observe that the voltage

profile is high, namely in the phases and busbars

MV/LV

Bus 2 3 4 5

(pu)

0.10+j0.05 0.10+j0.05 0.20+j0.15 ‐0.25+j0.05

(pu)

0.10+j0.05 0.00+j0.15 ‐0.20+j0.05 0.05+j0.00

(pu) 0.05+j0.05 ‐0.20+j0.05 0.05+j0.01 0.10+j0.05

1 2 3 4 5

0.95

1.05

1.1

1.15

1.2

phase voltages (pu)

1 2 3 4 5

0.01

0.02

0.03

neutral voltage (pu)

SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems

where the µG is connected (V

, V

). For

instance, in busbar 4, phase S, the voltage is higher

than 1.1 pu. The unbalance is noticeable as the

neutral voltage magnitude is significant.

In order to improve the voltage profile, the

control system features of the µGs may be used,

namely its capability to regulate reactive power.

3.2 Case 1: Reactive Power Control

This case-study concerns the effects of controlling

µG#4 (connected in phase S) in order that it absorbs

reactive power with tg(φ)=0.4. Figure 3 shows the

unbalanced load flow results for case-study 1.

Figure 3: Voltage at the three phases (R, S, T) and at the

neutral for case-study 1.

We can see that the improvement is marginal: the

voltage V

is now about 1.09 pu, against 1.1 pu

before this control action was undertaken. However,

voltage V

, which was 1.08 pu, is now close to

1.1 pu. The increase in the unbalance of the grid is

evidenced by the neutral voltage.

As this control action has shown to be not

effective, an alternative is to disconnect the µG. This

is to be dealt with in the next section.

3.3 Case 2: On/Off Control

Case-study 2 is related to the disconnection of

µG#4. The obtained results are shown in Figure 4.

As far as busbar 4 is concerned, the consequence

is now much more effective: voltage V

has

dropped to 0.96 pu. Nonetheless, other issues

emerged: voltages V

and V

have risen to 1.1 pu

and 1.09 pu, respectively. Globally, the network is

more unbalanced, as shown by the neutral voltage.

The next step is to disconnect the µG# 3, which

will be performed in case-study 3.

Figure 4: Voltage at the three phases (R, S, T) and at the

neutral for case-study 2.

3.4 Case 3: On/Off Cascade

For case-study 3 (disconnection of µG#3), the

obtained results are shown in Figure 5.

As would be expected, the problem associated

with busbar 3 was fixed, but the issue now is related

to busbar 5, whose voltage has increased to 1.13 pu.

It should be pointed out that the unbalance of the

network is even larger than before. In order to obtain

an acceptable voltage profile, µG#5 ought to be

disconnected. Under these conditions, it could be

shown that all busbar voltages would stay below

1.05 pu.

It has been illustrated that by disconnecting a

single µG a cascade may occur. Furthermore, it has

been shown that µG induced overvoltages are to be

mitigated by limiting the active power they can

inject in the grid, the reactive power control option

being much ineffective.

It would be desirable taking less extreme

measures to control voltage. A way of doing so is to

shed µG injection in steps instead.

Figure 5: Voltage at the three phases (R, S, T) and at the

neutral for case-study 3.

1 2 3 4 5

0.95

1.05

1.1

1.15

phase voltages (pu)

1 2 3 4 5

0.01

0.02

0.03

0.04

0.05

neutral voltage (pu)

1 2 3 4 5

0.9

0.95

1.05

1.1

1.15

phase voltages (pu)

1 2 3 4 5

0.02

0.04

0.06

0.08

neutral voltage (pu)

1 2 3 4 5

0.9

0.95

1.05

1.1

1.15

phase voltages (pu)

1 2 3 4 5

0.02

0.04

0.06

0.08

0.1

neutral voltage (pu)

VOLTAGECONTROLISSUESINLOWVOLTAGENETWORKSWITHMICROGENERATION

3.5 Case 4: Active Power Control

In this case-study, the control system will issue an

order of cutting off half of the active power injected

in busbar 4, phase S. The unbalanced load flow

results for this situation may be analysed in Figure 6.

Figure 6: Voltage at the three phases (R, S, T) and at the

neutral for case-study 4.

From Figure 6, one can conclude that this more

moderated action is enough to obtain an acceptable

voltage profile at the distribution network. The

voltage V

is equal to 1.03 pu and both the voltages

and V

are below 1.1 pu. Under these

circumstances, no further corrective action is

required.

4 VOLTAGE CONTROL USING

MV/LV TRANSFORMERS TAP

CHANGING

To illustrate the problems of voltage control using

MV/LV transformer tap changers, a similar

approach based on case-studies will be followed.

4.1 Case 1: The Effect of Elasticity

This case-study addresses a peak load situation with

unbalanced load and no injection by the µG. The test

network is represented in Figure 7, in which

= 0.525+j0.1715 pu for i=2, 3, 4 and 5.

Figure 7: Test network for case-study A; load peak

situation.

Power flow results are synthetized in Figure 8 for

the phase voltage changed induced by increasing the

voltage set-point of the transformer. This Figure

shows the maximum (ΔV

max

) and minimum (ΔV

min

)

bus voltage variation when the tap of the MV/LV

transformer changes from 1.05 pu to 1.075 pu. This

study was carried out for two types of load elasticity:

2 (constant impedance) and 0 (constant power).

Figure 8: Maximum and minimum bus voltage variation,

when the tap of the transformer changes from 1.05 pu to

1.075 pu; load elasticity: 2 (top) and 0 (bottom); case-

study 1.

The figure shows that the maximum bus voltage

variation follows closely the variation in the

transformer tap changer (ΔV

ref

=0.025 pu). However,

the minimum bus voltage variation does not. If the

load elasticity is 2, the minimum bus voltage

variation is smaller than the variation in the

transformer reference voltage; if the load elasticity is

0, the opposite behaviour is observed.

4.2 Case 2: Elasticity Opposite Effect

This case-study addresses an off-peak load situation

with both unbalanced load and µG. The test network

is represented in Figure 9, in which the load was

reduced to half the previous value and µG injected

power was set equal to two thirds of the previous

load. It should be remarked that the generators are

absorbing reactive power.

Figure 9: Test network for case-study 2; off-peak load

situation with microgeneration.

A summary of the power flow results is depicted

in Figure 10 for this case. This Figure shows the

maximum (ΔV

max

) and minimum (ΔV

min

) bus

1 2 3 4 5

0.95

1.05

1.1

1.15

phase voltages (pu)

1 2 3 4 5

0.01

0.02

0.03

0.04

neutral voltage (pu)

1 2 3 4 5

3 4 5

(

)

P-32

()

Q,P32 -

SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems

voltage variation, when the tap of the transformer

changes from 1.05 pu to 1.025 pu. The reduction in

the reference voltage set-point (ΔV

ref

=–0.025 pu) is

necessary because overvoltages are expected to

occur in this situation. As before, two elasticities

were considered.

Figure 10: Maximum and minimum bus voltage variation,

when the tap of the transformer changes from 1.05 pu to

1.025 pu; load elasticity: 2 (top) and 0 (bottom); case-

study 2.

From Figure 10, the following conclusions can

be undertaken:

• Regardless of the load type, the maximum bus

voltage reduction is always smaller than the

transformer reference voltage variation.

• For loads with elasticity of 2, the minimum bus

voltage variation follows closely the maximum bus

voltage variation.

• For loads with zero elasticity, the minimum bus

voltage variation is higher than the transformer

voltage variation.

The results of cases 1 and 2 allow the conclusion

that, in LV networks, changes in the transformer tap

may impact the feeder voltages in a way that is hard

to predict. The impact in minimum voltages can be

either amplified or reduced significantly depending

on the elasticity being small or large. This, together

with the need to regulate for both high voltages in

off-peak periods and low voltage in peak periods,

makes tap changing voltage regulation a difficult

approach to voltage control in LV networks.

5 CONCLUSIONS

Up to now, it is common knowledge that voltage

decreases along the feeders in LV networks, due to

the effect of the loads. However, this might not be

the case nowadays, with the increasing penetration

of small PV generators directly connected to the LV

grids. It is expected that the voltage rises in the

daylight, when the load is low and the generation is

high. The traditional voltage control method trough

proper management of reactive power flow is

ineffective, due to the high resistive characteristics

of the LV cables/lines. Therefore, active power

control is required and the disconnection of PV

microgeneration is the straightforward solution. This

paper tries to demonstrate that this drastic measure

may be avoided, if the PVs are able to receive

commands specifying the maximum power

generation level, when the voltage is out of its

acceptable operation range. In most cases, partial

generation shedding may prove effective to control

the voltage.

The issue of proper regulation of the taps of the

MV/LV transformer is also an important one. This is

hard to achieve because it must comply with a

twofold conflicting objective: on one hand, it must

mitigate the undervoltages during peak load periods

and, on the other hand, to control the overvoltages

during off-peak load periods. Furthermore, it has

been shown in the paper that transformer tap

changes effects are difficult to predict because they

depend on the load elasticity. This makes tap

changing voltage regulation a difficult approach to

voltage control in LV networks.

ACKNOWLEDGEMENTS

This work was partially supported by EDP

Distribuição via the InovGrid project.

REFERENCES

Monfared, M., Daryani, A. M., Abedi, A. M., 2006. Three

Phase Asymmetrical Load Flow for Four-Wire

Distribution Networks, 2006 IEEE PES Power

Systems Conference and Exposition, (PSCE’06),

Atlanta.

Ciric, M., Feltrin, A., Ochoa, L., 2003. Power Flow in

Four Wire Distribution Networks – General Approach,

IEEE Transactions on Power Systems, Vol.16, No.4.

Teng, J.H., Chang, C.Y., 2002. A Novel and Fast Three-

Phase Load Flow for Unbalanced Radial Distribution

Systems, IEEE Transactions on Power Systems,

Vol.17, No.4.

Chindriş, M., Anderu, A. S., Bud, C., Tomoiaga, B., 2007.

The Load Flow Calculation in Unbalanced Radial

Electric Networks with Distributed Generation, 9th

International Conference on Electrical Power Quality

and Utilization, (EPQU’2007), Barcelona.

Carvalho, P. M. S., Correia, P. F., Ferreira, L. A. M.,

2008. Distributed Reactive Power Generation Control

for Voltage Rise Mitigation in Distribution Networks,

VOLTAGECONTROLISSUESINLOWVOLTAGENETWORKSWITHMICROGENERATION

IEEE Transactions on Power Systems, Vol.28, No.2.

Thomson, M., Infield, D. G., 2007. Impact of Widespread

Photovoltaics Generation on Distribution Systems,

IET Renewables Power Generation, Vol.1, Iss.1.

Thomson, M., Infield, D. G., 2007. Network Power-Flow

Analysis for a High Penetration of Distributed

Generation, IEEE Transactions on Power Systems,

Vol.22, No.3.

Chen, T., Yang, W., 2001. Analysis of multi-grounded

four-wire distribution systems considering the neutral

grounding, IEEE Transactions on Power Delivery,

Vol.16, No.4.

Meliopoulos, A., Kennedy, J., Nucci, C., Borghetti, A.,

Contaxis, G., 1998. Power distribution practices in

USA and Europe: Impact on power quality, 8

IEEE

International Conference on Harmonics and Quality

of Power, Vol.1.

SMARTGREENS2012-1stInternationalConferenceonSmartGridsandGreenITSystems