A UML & Spatial OCL based Approach for Handling Quality Issues

in SOLAP Systems

Kamal Boulil, Sandro Bimonte and Francois Pinet

Irstea, UR TSCF, 24 avenue des Landais, 63172 Aubière, France

Keywords: Spatial DataWarehouse, Spatial OLAP, Quality, UML, OCL, Integrity Constraints.

Abstract: Spatial Data warehouses and Spatial OLAP systems are Business Intelligence technologies allowing

efficient and interactive analysis of large geo-referenced datasets. In such a kind of systems the goodness of

analysis depends on: the warehoused data quality, how aggregations are performed, and how warehoused

data are explored. In this paper, we propose a framework based on a UML profile and OCL-defined

integrity constraints to grant quality in the whole SOLAP system. We also propose an automatic

implementation in a classical ROLAP architecture to validate our proposal.

1 INTRODUCTION AND

MOTIVATION

Spatial Data Warehouse (SDW) and Spatial OLAP

(SOLAP) systems are Business Intelligence (BI)

technologies allowing effective storage and on-line

spatio-multidimensional analysis of huge volumes of

geo-referenced data which can be collected from

multiple heterogeneous data sources (Malinowsky et

al., 2008). These systems are based on the spatio-

multidimensional model, which extends the

conventional OLAP model with spatial concepts

such as spatial measures and spatial dimensions

which provide support for the representation and

storage of spatial data, and spatial operators

allowing users to interactively explore and aggregate

warehoused data. A typical Spatial Relational OLAP

(Spatial ROLAP) architecture is composed of three

tiers: (i) the SDW tier historizes and manages

integrated (spatial) data using a spatial Relational

DBMS; (ii) the SOLAP server implements SOLAP

operators that compute and handle spatial data

cubes; (iii) the SOLAP client tier provides decision-

makers with interactive visual displays that trigger

SOLAP operators.

The heterogeneity of data sources in these

systems may lead to several data quality problems

(Boulil et al., 2011). In order to grant data quality in

SDW, some approaches have been proposed to

“repair” data by means of statistical techniques, data

mining techniques, etc. (Ribeiro et al., 2011). At the

same time, Integrity Constraints (IC) have been

recognized as effective methods to express rules that

control the consistency and completeness of

warehoused spatial data (Salehi, 2009). Moreover,

the goodness of spatio-multidimensional analysis

also depends on the correct aggregation of measures

in respect to summarizability conditions (or

aggregation constraints), which check for example

that the measure and aggregate function types are

compatible (Lenz et al., 1997). However, in SOLAP

systems the goodness of the analysis also requires

another control when exploring (aggregated) data in

order to avoid misinterpretation of meaningless

SOLAP query results (Levesque et al., 2007), e.g.,

the query "Sales per country after December 26,

1991" returns empty results for USSR that could be

interpreted by users as an absence of sales instead of

realizing that a result is impossible for this period.

On the other hand, conceptual design of complex

systems such as data warehouses has been widely

recognized as being necessary for successful BI

projects (Malinowski and Zimányi, 2008) since it

allows designers defining schemas that are easy to

understand by decision makers. In this context,

UML (Unified Modeling Language) is widely

accepted as the Object-Oriented standard for

modelling various aspects of software systems, and

also SDW systems (Pinet and Schneider, 2009).

Indeed, any approach using UML minimizes the

efforts of designers and decision-makers in

developing and implementing the data schema. It

can be also interpreted by CASE tools. In the same

Boulil K., Bimonte S. and Pinet F..

A UML & Spatial OCL based Approach for Handling Quality Issues in SOLAP Systems.

DOI: 10.5220/0003967100990104

In Proceedings of the 14th International Conference on Enterprise Information Systems (ICEIS-2012), pages 99-104

ISBN: 978-989-8565-10-5

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

way, defining IC at a conceptual level allows

handling quality issues at the early stages of

development (Boulil et al., 2011), minimizing

implementation efforts. In this context, (Ghozzi et

al., 2003) propose ad-hoc conceptual

multidimensional models allowing the expression of

some data IC by means of logical predicates.

(Malinowskiand Zimányi, 2008) propose an

extension of the ER model for the design of spatio-

temporal data warehouses. They define a set of ad-

hoc pictograms to express spatial data IC (i.e.,

spatial topological relationships between spatial

members). (Glorioand Trujillo, 2008) propose a

UML profile for SDW, but they consider a very

small number of data IC. A survey on aggregation

issues is presented in (Mazón et al., 2009). They

express simple structural constraints (e.g., facts

should be linked to dimensions with one-to-many

associations) with UML multiplicities. In (Pinetand

Schneider, 2009), complex structural aggregation

constraints are expressed with Object Constraint

Language (OCL). OCL represents an effective

solution to define data IC at the conceptual level in a

clear, non-ambiguous and platform-independent

way. Indeed, (Boulil et al.2011) present the

definition, on the top of a UML-based SDW

conceptual model, of a large number of data IC on

warehoused spatial data by means of Spatial OCL,

which is an extension of OCL for spatial data (Pinet

et al., 2007). They also propose an automatic

implementation in the Spatial DBMS Oracle Spatial

11g. (Lavesque et al., 2007) propose a framework

for identifying quality risks in ETL, and SOLAP

systems. They define 3 types of quality problems

(data sources, OLAP data cubes and GIS

functionalities) and define them by means of paper

forms. They also propose an implementation in the

JMAP SOLAP system.

Finally, to best of our knowledge, no work

proposes a unique framework to express at the

conceptual abstraction level IC on spatial

warehoused data, aggregation, and spatio-

multidimensional queries, and their automatic

implementation in a classical ROLAP architecture.

Thus, in this paper we present three main

contributions.

For first, we extend/reformulate the definition of

(S)DW IC for handling quality issues in SOLAP

systems; we use IC to perform three quality control

types:

(a) Data quality control ensures that warehoused

spatial data are valid (e.g., geometries of cities must

be topologically included in the geometries of their

states);

(b) Aggregation quality control ensures that

aggregations of measures are correct and meaningful

(e.g., the sum of the unit prices does not make sense)

(Lenz et al., 1997);

interpretation induced by meaningless SOLAP query

results (e.g., sales in USSR after 26 December 1991)

(misuse data cube risks as defined by (Levesque et

al., 2007)).

Secondly, motivated by a lack of a unique

conceptual framework to define SOLAP IC, we

propose a UML-OCL based conceptual framework.

Finally, we propose an automatic implementation of

such framework in a classical Relational SOLAP

architecture.

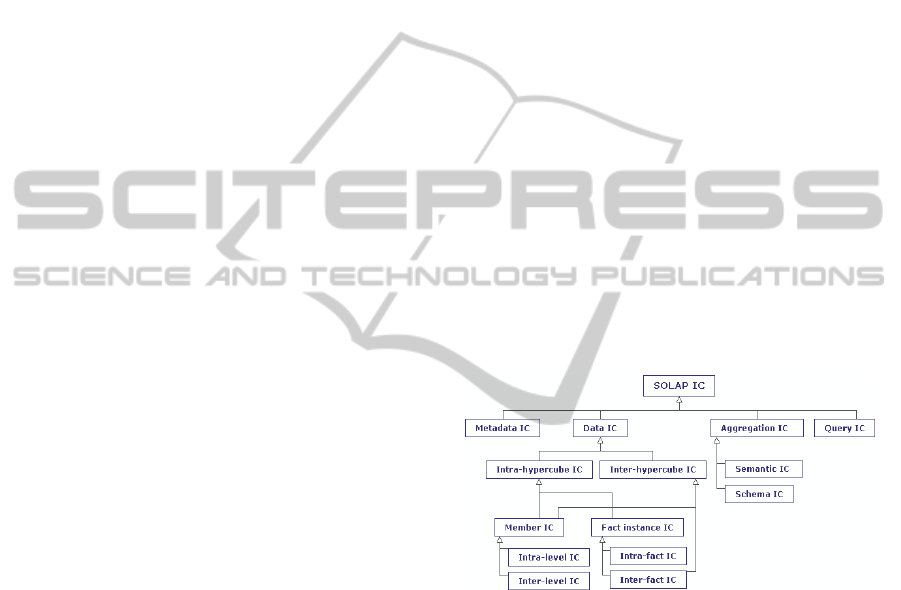
2 SOLAP IC CLASSIFICATION

In this section, we present an extension of our

previous SDW IC classification (Boulil et al., 2011)

by introducing a new class, Query IC class. This

classification (Figure 1) serves as a reference guide

for the process of handling the three types of quality

issues in a SOLAP system.

Figure 1: SOLAP IC classification.

Before detailing the classification, we present the

case study which will be used all along the paper to

describe our proposal. It concerns an environmental

SDW, with a temporal dimension that groups days

into months and months into years, and a spatial

dimension representing cities with their regions and

countries. The measure is the temperature value.

Using this SDW, decision-makers can answer to

SOLAP queries like these:”What is the minimal

temperature per year and country?” or “What is

average temperature per month and country?”. In

order to answer these queries, decision-makers use

the min and average aggregate functions to

aggregate the temperature values.

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

100

Let us now provide explanations and some

examples of these IC classes using the previously

described case study.

As shown in (Boulil et al., 2011), Metadata IC

verify the consistency of metadata of different

integrated data sources (e.g., spatial members and

measures must be defined with the same geographic

scale).

Data IC ensure the logical consistency and

completeness of warehoused spatial data, for

example:

Example 1: “the geometry of each city must be

topologically included in the geometry of its region”

Example 2: "no facts (e.g., temperature values)

should exist for USSR after 26 December 1991".

These constraints can be defined on all elements of

the SDW such as facts, members, etc.

Aggregation IC guarantee correct and

meaningful aggregations of measures. In particular,

semantic constraints address the problem of the

applicability of aggregate functions to measures

according to the semantic nature and the type of

measures, aggregate functions and dimensions. For

example:

Example 3: “Sum of temperature values does not

make sense”

Schema constraints are conditions that must be

satisfied by dimension hierarchies and dimension-

fact relationships to avoid double counting and

incomplete aggregates. For example, dimensions and

facts should be linked by one-to-many relationships

(Mazón et al., 2009).

Query IC refer to conditions that guarantee that

SOLAP queries are valid in the sense that their

results are not always empty in order to avoid

problems of misinterpretation. For example, the

SOLAP query “What are the average temperatures

in USSR in 2010?” returns an empty result since no

temperature value is stored for USSR after 26

December 1991 (the previous data IC of Example 2).

Even if this IC is implemented as data IC, classical

SOLAP tools allow decision-makers to formulate

this query by combining these two members (USSR

and 2010) returning an empty value. This leads to a

problem of interpretation: this empty value may be

perceived as if there were no temperature values

registered for USSR during 2010, instead of

realizing that this combination of members (USSR

and 2010) is invalid. Consequently, to avoid this

misinterpretation we define the following query

constraint:

Example 4: "It is incorrect to combine USSR with

days after 26 December 1991 in a SOLAP query".

Although, this query example could be resolved by

using particular spatio-multidimensional data

structures such as DW versioning structures, Query

IC allow designers to model any invalid query which

can be independent of time-versioning aspects (for

example, some products cannot be sold in certain

stores).

3 THE FRAMEWORK

Before describing our conceptual framework for

defining SOLAP IC, we present main concepts of a

UML profile and Spatial OCL.

The UML profiles are a way to customize UML

for particular domains or platforms by extending its

metaclasses (class, property, etc.). A profile is

defined using three extension mechanisms:

stereotypes, tagged values and constraints. A

stereotype is an extension of a UML metaclass.

Tagged values are properties of stereotypes. Finally,

a set of OCL constraints precise each stereotype's

application semantics. OCL provides a platform-

independent method to model constraints. It can be

interpreted by code generators to generate code

automatically. OCL constraints can be defined at the

meta-model level (e.g., UML profile) and also at the

model level (the profile instance). Spatial OCL is an

extension of OCL that supports spatial topological

relationships (inside, intersect, etc.) (Pinet et al.,

2007).

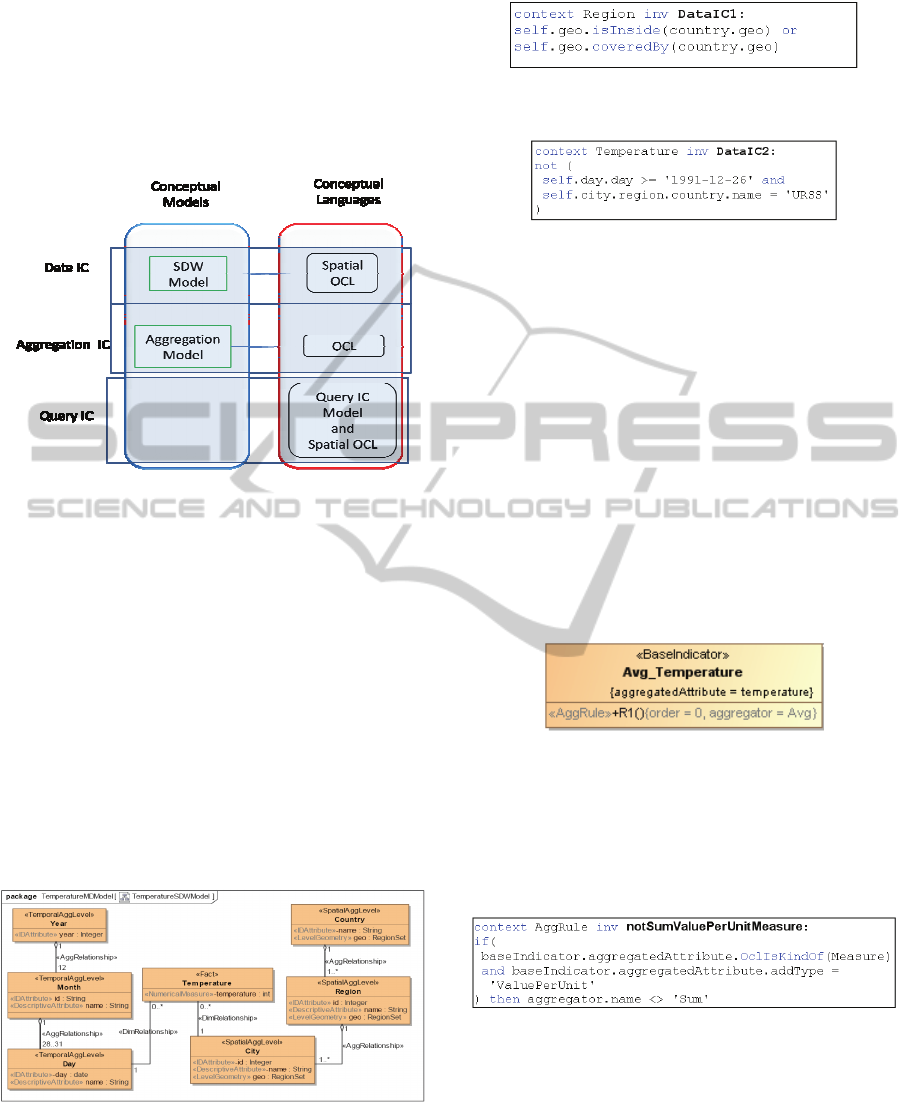
In order to define SOLAP data, aggregation and

query IC at a conceptual level, we propose a

framework based on a UML profile and Spatial OCL

(Figure 2).

The main idea is to a have a unique UML profile

that defines 3 interconnected models to conceptually

represent:

a) SDW data structures (SDW model),

b) how measures are aggregated to meet the

analysis requirements (Aggregation model), and

c) Query IC model

and then define IC with Spatial OCL using these

models. In particular Data IC are defined by

designers using Spatial OCL on the top of the

instance of SDW model, Aggregation IC are defined

as Aggregation model’s stereotypes constraints

using OCL, and Query IC are defined using the

Query IC model and Spatial OCL. Due to space

reasons we do not detail the proposed profile, but we

provide some examples. Details on the SDW and

aggregation models can be found in (Boulil et al.,

AUML&SpatialOCLbasedApproachforHandlingQualityIssuesinSOLAPSystems

101

2011). It is important to note that we have chosen to

define a UML profile instead of a metamodel since

the UML metamodel’s elements are sufficient to

capture all the SOLAP applications' semantics

including all the multidimensional data structures

(Glorioand Trujillo, 2008) and all the identified IC

types.

Figure 2: UML-OCL based conceptual framework.

The SDW model allows the definition of SDW

data structures and the expression of Data IC on the

top of these structures using Spatial OCL (Boulil et

al., 2011).

The SDW case study represented using the SDW

model is shown on Figure 3. This SDW model

instance contains two dimensions: (i) a spatial

dimension composed of 3 spatial levels (stereotyped

as <<SpatialAggLevel>>), City, Region and

Country; and (ii) a temporal dimension composed of

three temporal levels Day, Month and Year. The

numerical measure temperature

(<<NumericalMeasure>> stereotype) is defined as

an attributed of the fact class Temperature

(<<Fact>> stereotype).

Figure 3: A SDW model instance.

Once the SDW model instance has been defined,

data integrity constraints can be expressed using

Spatial OCL. For example, the Data IC of Example

1 is expressed as follows:

The Data IC of Example 2 is expressed using

OCL in the following way:

The Aggregation model represents how measures

are aggregated along dimensions according to

decision-makers' analysis needs. The instance of

Aggregation model for our case study, which

represents that the temperature measure

(aggregatedAttribute tagged value) is aggregated

along all the dimensions using the average aggregate

function (aggregator=Avg tagged value), is depicted

in Figure 4.

In (Boulil et al., 2011) we have identified a set of

aggregation constraints that grant meaningful

aggregations of measures. These constraints are

valid for all SOLAP applications. Thus, we have

implemented them as OCL constraints in the

Aggregation Model package of the profile. They are

checked by the CASE tool at the design stage when

validating the conceptual model.

Figure 4: Aggregation model instance.

For example, in order to force the user to not

aggregate non-additive (or value per unit) measures

(for example the temperature; Example 3) using the

sum aggregate function, the following OCL

statement is defined in the profile:

Finally, designers can express IC on SOLAP

queries using the Query IC model. Typically, a

SOLAP query is a combination of measures and

members from different dimensions. Thus, the

Query IC model can be used for example to define

invalid combinations of member sets. These member

sets are specified as attributes with the

<<MemberSet>> stereotype. The value domain of a

<<MemberSet>> attribute is a subset of members of

a dimension level, whose definition is precised with

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

102

the condition tagged value, which is an OCL

statement defined on the context of the dimension

level to select a subset of its members.

An example of an instance of the Query IC

model is depicted on Figure 5, where the user states

that combining days (<<MemberSet>> day) after 26

December 1991 (condition= After1991-12-26,

whose OCL expression is shown in Figure 6) with

the USSR (<<MemberSet>> country) is meaningless

in any SOLAP query.

Figure 5: Query IC model instance.

Figure 6: OCL used by the Query IC of Figure 5.

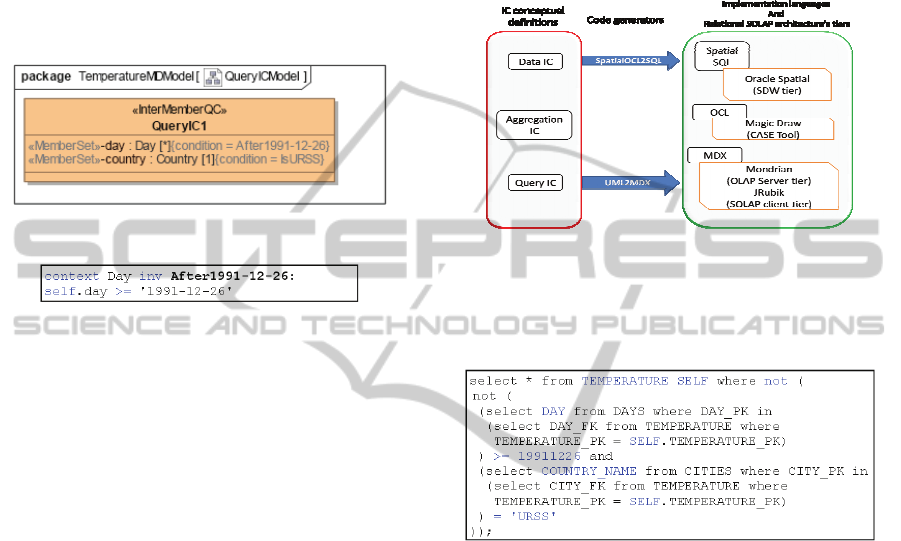
4 IMPLEMENTATION

In this section, we present our architecture to

automatically implement SOLAP IC (Figure 7). The

main idea is to automatically implement each kind

of IC in a different tier of the SOLAP architecture.

The conceptual definition of each IC is

automatically translated into the implementation

language used by each tier. In particular, Data IC are

translated using SpatialOCL2SQL and implemented

in the SDW tier; Query IC are translated by our

automatic code generator (called UML2MDX) and

implemented in the OLAP server and the SOLAP

client, and finally Aggregation IC are implemented

in our UML profile using OCL and controlled

during the design stage by the MagicDraw CASE

tool.

Our SOLAP architecture (Figure 7) is based on:

the Spatial DBMS Oracle Spatial 11g, the ROLAP

Server Mondrian and a SOLAP client JRubik.

Mondrian connects to a relational database and

enables the execution of OLAP queries expressed

using MDX (MultiDimensional eXpressions) that is

a standard language for querying multidimensional

databases. JRubik provides a graphical presentation

layer on top of Mondrian and allows cartographic

representations of OLAP queries using the SVG

format.

In order to automatically implement data IC in

the Oracle Spatial 11g, we have used the code

generator Spatial OCL2SQL. Spatial OCL2SQL is a

Java open source tool which integrates the spatial

extensions of OCL called OCL 9IM and OCL ADV

(Pinet et al., 2007). It automatically generates SQL

scripts for Oracle Spatial from Spatial OCL

conceptual constraints.

Figure 7: Automatic implementation of SOLAP IC.

In our case study, the previously defined OCL

data IC of Example 2 is transformed in the following

SQL query:

This query selects the facts (TEMPERATURE

table's tuples) that do not satisfy the constraint of

Example 2.

The Aggregation IC are implemented as OCL

profile inherent constraints in the MagicDraw CASE

tool. MagicDraw supports OCL at the meta-model

level (UML profile). In other terms, MagicDraw is

able to check OCL constraints defined on UML

stereotypes. This allows checking Aggregation IC at

design stage independently of the specific SOLAP

architecture used and without providing any

implementation efforts. For example, if the designer

defines an instance of the Aggregation model by

using the Sum for the temperature measure,

MagicDraw checks the OCL Aggregation IC of

Example 3 and informs him that the constraint is

violated.

In order to implement Query IC, we use MDX,

which is the defacto standard of OLAP Servers and

Clients. Thus, the choice of Mondrian as OLAP

server is not a limitation for our generic architecture.

The main idea is to translate the Query IC into MDX

AUML&SpatialOCLbasedApproachforHandlingQualityIssuesinSOLAPSystems

103

formula, which are stored in the OLAP Server and

then visualized in the SOLAP client. These

formulas, when executed, inform user about the

quality of query results. For each Query IC type we

have defined an MDX template. The templates are

fulfilled using a Java method (UML2MDX) that

parses the XMI files associated to the Query IC.

Different visual policies are associated with different

combinations of members from these sets to be

displayed in the SOLAP client tier: green colour for

valid cells, yellow colour for aggregated cells that

include valid and invalid cells and red colour for

invalid cells. Figure 8 shows an example of OLAP

query where these visual policies are applied

according the MDX formula implementing the

Query IC of Figure 6: valid cells such as those

combining USSR with dates before 1991-12-26 (e.g.

1991-12-01) are displayed with green colour; invalid

cells that involve for example USSR and dates after

1991-12-26 (e.g. 1991-12-27, 2010-1, 2010) are

displayed with red colour, other cells are displayed

with yellow colour, such as 1991-12 with USSR

because it is the aggregation of valid (e.g. 1991-12-

01 with USSR) and invalid cells (e.g. 1991-12-27

with USSR).

Figure 8: Query IC visualization of Example 4.

5 CONCLUSIONS

In this paper, we first show that the SOLAP analysis

goodness depends on 3 quality types: data,

aggregation and query qualities. Thus, we (i) extend

the concept of integrity constraints to consider all

these quality types; (ii) propose a framework based

on a UML profile and Spatial OCL to express these

SOLAP IC at the conceptual level; and (iii) show

their automated implementations in a typical

ROLAP architecture. Our current work is on

improving the UML2MDX tool by integrating

Spatial MDX expressions and defining cartographic-

related visualization policies in order to implement

spatial query IC.

As in our current automatic implementation only

considers the snowflake schema SDW

implementations, we are working on the

consideration of the star-schema implementations.

Finally, we will work on the formal validation of the

completeness of our classification, and the

expressiveness of our conceptual framework.

REFERENCES

Boulil, K., Bimonte, S., Pinet, F. (2011). Un modèle UML

et des contraintes OCL pour les entrepôts de données

spatiales : De la représentation conceptuelle à

l'implémentation. Ingénierie des Systèmes

d'Information, 16(6) 11-39

Ghozzi, F., Ravat, F., Teste, O., Zurfluh, G. (2003).

Constraints and Multidimensional Databases. In 5th

International Conference on Enterprise Information

Systems, 104-111

Glorio, O. and Trujillo, J. 2008. An MDA Approach for

the Development of Spatial Data Warehouses. In 10th

International Conference on Data Warehousing and

Knowledge Discovery, Berlin-Heidelberg: Springer,

23-32

Lenz, H.-J. and Shoshani, A. 1997. Summarizability in

OLAP and statistical data bases. In International

Conference on Scientific and Statistical Database

Management, IEEE, 132-143

Levesque, M.-A., Y. Bédard, M. Gervais, R. Devillers,

(2007). Towards managing the risks of data misuse for

spatial datacubes. In 5th International Symposium on

Spatial Data Quality, June 13-15, Enschede,

Netherlands

Malinowski, E. and Zimányi, E. (2008). Advanced Data

Warehouse Design: From Conventional to Spatial and

Temporal Applications. Berlin: Springer-Verlag.

Mazón, J.-N., J. Lechtenbörger, et al. (2009). A survey on

summarizability issues in multidimensional modeling.

Dataand Knowledge Engineering 68(12): 1452-1469.

Pinet, F., Duboisset, M. and Soulignac, V. (2007). Using

UML and OCL to maintain the consistency of spatial

data in environmental information systems.

Environmental modellingand software, 22(8) 1217-

1220

Pinet, F., Schneider, M. (2009) A Unified Object

Constraint Model for Designing and Implementing

Multidimensional Systems. Journal of Data Semantics

13, 37-71

Ribeiro, L., Goldschmidt, R., Cavalcanti, M. 2011.

Complementing Data in the ETL Process. In 13th

International Conference Data Warehousing and

Knowledge Discovery, Berlin-Heidelberg: Springer,

112-123

Salehi, M. (2009). Developing a Model and a Language to

Identify and Specify the Integrity Constraints in

Spatial Datacubes. Doctoral thesis. Faculté des études

supérieures de l’Université Laval, Canada.

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

104