Construction of Fuzzy Sets and Applying Aggregation Operators for

Fuzzy Queries

Miroslav Hudec

and František Sudzina

Institute of Informatics and Statistics, Dubravská cesta 3, Bratislava, Slovakia

School of Business and Social Sciences, Aarhus University, Falstersgade 50, Aarhus, Denmark

Keywords: Fuzzy Queries, Construction of Fuzzy Sets, Aggregation Operators, Database.

Abstract: Flexible query conditions could use linguistic terms described by fuzzy sets. The question is how to

properly construct fuzzy sets for each linguistic term and apply an adequate aggregation function. For

construction of fuzzy sets, the lowest value, the highest value of attribute and the distribution of data inside

its domain are used. The logarithmic transformation of domains appears to be suitable. This way leads to a

balanced distribution of tuples over fuzzy sets. In addition, users’ opinions about linguistic terms as well as

current content in database are merged. The second investigated issue is selection of an adequate

aggregation operator. Usual t-norm functions as well as compensatory γ – operator have been examined.

Finally, the interface for managing these issues has been proposed. A user can obtain an overview about

stored data before running a query; that may reduce empty or overabundant answers.

1 INTRODUCTION

Users query databases in order to obtain data needed

for analysis or decision making. The common way

how to realise such a query is to formulate a logical

condition. In general, a logical condition consists of

several atomic (elementary) conditions connected

with logical and or or operators. Querying with

imprecision allows users to implement linguistic

terms to better qualify data they wish to obtain. An

example of such a query is select small departments

with high turnover. The linguistic terms clearly

suggest that there is a smooth transition between

acceptable and unacceptable records.

The fuzzy set theory (Zadeh, 1965) is a rational

option which offers the solution. It brings a

paradigm in dealing with the graduation, uncertainty

and ambiguity described by linguistic terms. Main

reasons to use fuzzy logic in queries are discussed in

(Dubois and Prade, 1997) and advocated in

(Kacprzyk and Zadrożny, 2001).

The matching degree critically depends on

constructed membership functions of all linguistic

terms (Klir and Yuan, 1995); (Meier et al., 2005)

and chosen logical aggregation function. The former

issue has been examined in (Kacprzyk and

Zadrożny, 2001); (Tudorie, 2008); (Tudorie, 2009).

There exist many different operators which calculate

conjunctions and disjunctions of membership values

(Zimmermann, 2001). Usually, in practical

realisations, the minimum t-norm is used as an

aggregation function for and operator.

Our paper is focused on these two issues of fuzzy

queries. Section 2 shortly presents basic concepts of

fuzzy queries. Section 3 is devoted to construction of

membership functions of linguistic terms used in

queries. Section 4 is focused on calculation of query

matching degree by aggregation functions. Section 5

presents suggested user interface for managing

examined issues of fuzzy queries. Finally, some

conclusions are drawn in section 6.

2 PRELIMINARIES OF FUZZY

QUERYING

Let R be a table or relation of a relational database.

A set of tuples t is then defined as relation on

Cartesian product in the following way:

)}( )(|{

1 n

ADomxxADomttR "

∈

⊆

(1)

where A

is the database attribute (table column) and

Dom(A

) is its associated domain. In our case,

domains are set of real numbers or its subsets.

In queries based on fuzzy logic, the database

253

Hudec M. and Sudzina F..

Construction of Fuzzy Sets and Applying Aggregation Operators for Fuzzy Queries.

DOI: 10.5220/0003968802530258

In Proceedings of the 14th International Conference on Enterprise Information Systems (ICEIS-2012), pages 253-258

ISBN: 978-989-8565-10-5

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

record (tuple) can fully or partially satisfy the intent

of a query Q. Let A(Q) be the set of answers to query

Q defined in the following way:

}0)(|))(,{()( >∧

∈

= tRtttQA

(2)

where µ(t) indicates how well the selected tuple t

satisfies a query criterion. It is expressed as a

number from the [0, 1] interval.

Several fuzzy query implementations have been

proposed such as FQUERY (Kacprzyk and

Zadrożny, 1995), SQLf (Bosc and Pivert, 2000),

FQL (Wang et al, 2007), FuzzyKAA (Tudorie,

2009) and fuzzy generalized logical condition

(Hudec, 2009). “Although there are variations

according to the particularities of different

implementations, the answer to a fuzzy query

sentence is generally a list of records, ranked by the

degree of matching” (Branco et al, 2005, p. 21). The

value of matching degree depends on membership

functions constructed for each elementary query

condition and on chosen aggregation function.

3 CONSTRUCTION OF

MEMBERSHIP FUNCTIONS

If the system uses badly defined membership

functions, it will not work properly. These functions

have to be carefully defined (Galindo, 2008). This

issue has two main aspects. In the first aspect, users

define parameters of membership functions

according to their reasoning and preferences. The

second aspect is devoted to calculation of these

parameters from data stored in a database.



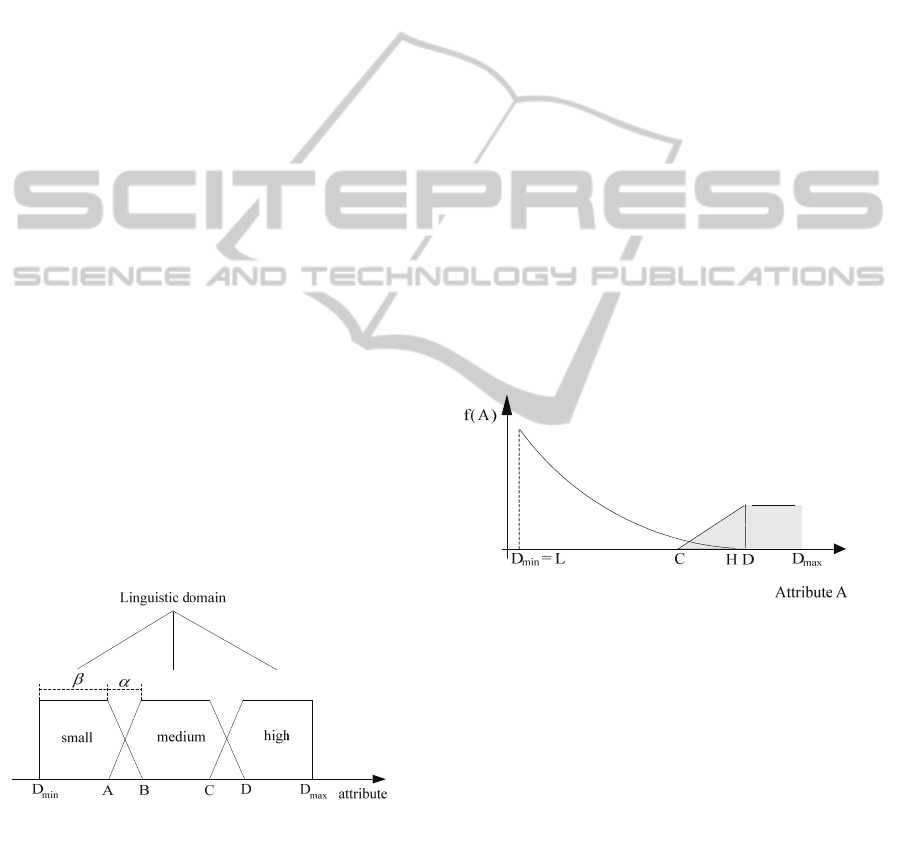
Figure 1: Linguistic and crisp domain.

Let a linguistic domain consists of linguistic

terms {small, medium, high}. Linguistic domain

covers crisp domain of attribute in a way shown in

Figure 1. Let D

mim

and D

max

be the lowest and the

highest domain values of attribute A i.e. Dom(A) =

min

, D

max

]. Let L be the lowest boundary value and

H be the upper boundary value of attribute in current

content of a database; that is, [L, H]

⊆ [D

min

max

]. In case of attribute number of days with

empty supply shelves, the domain is the [0, 365]

interval of integers. For example, empty shelves for

all spare parts are noticed between 7 and 75 days i.e.

L=5 and H=75.

3.1 Users Create Fuzzy Sets

Parameters

In this approach, users are required to choose

parameters A, B, C and D (Figure 1) according to

their reasoning and preferences. Therefore, these

parameters are applied in a query realization phase.

Detailed discussion on how to cope with this issue

can be found in (Klir and Yuan, 1995). Users usually

consider their preferences on the whole domain of

attributes. Let’s have the attribute A defined on

domain Dom(A) = [D

Amin

, D

Amax

]. Let values for all

records be non-uniformly distributed inside domain

in such a way that majority of records are

concentrated near value L whereas few records have

value of the attribute A near the value H (Figure 2).

If a user decide to set parameters C and D for the

condition attribute A is high as is depicted in the

Figure 2 only few records meet the condition.

Figure 2: Fuzzy set high for the attribute A.

If the query is more restrictive (conjunction of

several atomic conditions) and distribution of values

is highly unbalanced, it may easily end up with an

empty answer.

3.2 Fuzzy Sets Construction from the

Current Content of a Database

This problem was initially examined for fuzzy

queries where the second elementary condition

depends on the result of the first elementary

condition. It means that the second elementary

criterion requires taking into account sub domains of

the attributes domains limited by tuples already

selected by the first elementary condition (Tudorie,

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

254

2008). Two ways of fuzzy sets construction are

offered: the uniform domain covering method and

the statistical mean based algorithm. In our research,

we have examined these methods for fuzzy queries

where overall query condition consists of atomic

conditions connected by and operator.

3.2.1 Uniform Domain Covering Method

At the beginning, this method requires the values of

L and H. These values are obtained form a database

content. Length of fuzzy set core β and length of

fuzzy set slope α (Figure 1) are created in the

following way (Tudorie, 2008):

)(

LH −=

(3)

)(

LH −=

(4)

Consequently, it is easy to calculate required

parameters A, B C and D from values L, H, α and β.

The uniform domain covering method reduces

the issue depicted in Figure 2, if the distribution of

attribute values in the domain is more or less

uniform.

If it is not the case, the uniform domain coverage

could lead to a highly unbalanced distribution of

tuples over fuzzy sets. It implies that only few tuples

are in one fuzzy set, while majority of tuples is in

another one. It might lead to a conclusion that the

meaning of the linguistic term is far from real data.

Let’s have a query, which looks for sellers with a

high amount of sold items. The query condition has

to consider parameters of each region where sellers

operate. The meaning of the term high differs among

regions.

3.2.2 Statistical Mean based Algorithm

A possible solution is adding the statistical mean

into construction of fuzzy sets. The middle of the

medium fuzzy set core is the statistical mean of

attribute. In this approach, cores of all three fuzzy

sets (β) have equal size; lengths of fuzzy sets slopes

are different. Experiments on altitude above sea

level for 2877 municipalities in Slovakia reveal a

limitation of this approach. Many municipalities are

close to the value L, whereas only few municipalities

are close to H. It is similar to the distribution

depicted in Figure 2. Moreover, the value of β is

smaller in comparison with the uniform domain

covering method. This causes that only two

municipalities fully belong to the fuzzy set high. In

order to solve this limitation, we have realised

experiments with a logarithmic transformation.

3.2.3 Logarithmic Transformation

In many cases, values of attributes are close to e.g.

the value L, whereas only few are close to H and

therefore belong to the fuzzy set high or contrary.

An illustrative example is population density of

municipalities where only few big cities have high

population density. This kind of data distribution

where only few tuples highly determine fuzzy set

parameters cannot be properly evaluated by uniform

domain covering method or by the linear

transformation used in (Kacprzyk and Zadrożny,

2001). The logarithmic transformation is a rational

option which might provide a solution. After a

logarithmic transformation, the values of α and β are

not equally long for all fuzzy sets. The interval [L,

H] is transformed into the interval [log(L), log(H)].

Consequently, in this interval, logarithms of α, β and

A, B, C and D are calculated using equations (3) and

(4). Finally, obtained values are delogarithmised into

real values.

4 CALCULATION OF

MATCHING DEGREE

The most used operators are t-norm and t-conorm

functions; they are specialized for the aggregation

under uncertainty (Detyniecki, 2001). In this paper,

other aggregation operators are mentioned.

4.1 T-norm Functions

They are generalizations of the two-valued logical

aggregation operators. The associative axiom (Klir

and Yuan, 1995) ensures that all t-norm and t-

conorm functions can be used for and and or

operators respectively. Actually, it is not easy to

aggregate all these functions to arbitrary number of

elementary conditions. The following t-norm

functions can be easily aggregated for cases when

more than two attributes are used (Siler and

Buckley, 2005):

 minimum

n1,...,i ))(amin((t)

(5)

 product

∏

))(a((t)

μμ

(6)

 Lukasiewicz

ConstructionofFuzzySetsandApplyingAggregationOperatorsforFuzzyQueries

255

)1)(,0max((t)

∑

+−=

μμ

(7)

where µ

) denotes the membership degree of the

attribute a

to the i-th fuzzy set.

It is obvious that different t-norm functions

calculate different matching degrees. In addition,

they do not meet all axioms of Boolean logic. It is

consequence of generalization of {0, 1} logic into

many-valued logics (including fuzzy logic) based on

truth functionality. The two-valued logic meets all

axioms of Boolean algebra, namely excluded

middle, contradiction and idempotency whereas in

fuzzy logic it is not the case (Radojević, 2008).

From the above mentioned t-norms, only

minimum (5) is an idempotent t-norm what makes it

the most acceptable for users accustomed to the

crisp logic. On the other hand, this t-norm does not

meet the contradiction axiom. The product t-norm

(6) takes into account all membership degrees and

balances the query truth membership value across

each of elementary conditions. But the query

matching degree could be significantly lower than

the matching degree of the lowest value of

elementary conditions. In addition, this t-norm does

not meet the contradiction and the idempotency

axioms. The Lukasiewicz t-norm (7) is a nilpotent t-

norm. This t-norm satisfies the contradiction axiom

but does not satisfy the idempotency axiom.

Let’s have two records which satisfy the first

elementary condition (A) and the second elementary

condition (B) as is shown in Table 1.

Table 1: Example of matching degrees using t-norms.

tuple A B Min (5) Prod (6) Luk (7)

1 0.11 0.2 0.11 0.02 0

2 0.1 0.9 0.1 0.09 0

It is obvious that the min-t-norm prefers the tuple

1. This contradicts the human decision-making

process. Although the tuple 1 is only slightly better

according to the first elementary condition and

significantly worse according to the second

elementary condition, it is preferred. The product t-

norm prefers the second record with the membership

degree lower than 0.1. Lukasiewicz t-norm

calculates membership degrees of 0 for both records

because they do not significantly satisfy both atomic

conditions.

4.2 Other Aggregation Functions

“Several authors noticed that t-norms and t-conorms

lack compensational behaviour” (Detyniecki, 2001,

p.28). This issue can be solved using compensatory

operators to model the fuzzy or linguistic and

operator. The compensation of a bad value of one

attribute by a good value of another attribute can be

achieved e.g. by the γ - operator (Zimmermann and

Zynso, 1980) adapted to the fuzzy queries in the

following way:

γγ

μμμ

)))(1(1())(()(

∏∏

−

−−=

iii

aat

(8)

where

]1,0[

∈

, other elements have the same

meaning as in (5) – (7). Applying the γ - operator

with the value of 0.5 implies that all attributes are

equally relevant in the calculation of the matching

degree. A short discussion of applicability of γ -

operator can be found in (Werro et al, 2005).

Let’s look at the query containing two

elementary conditions. The matching degrees of all

above mentioned t-norm functions and γ - operator

are presented in Table 2.

Table 2: Matching degrees using t-norms and γ = 0.5.

tuple A B min (5) prod (6) L (7) γ (8)

1 0.1 0.1 0.1 0.01 0 0.04

5 0.11 0.2 0.11 0.02 0 0.08

3 0.1 0.9 0.1 0.09 0 0.29

8 0.33 0.42 0.33 0.14 0 0.29

4 0.1 1 0.1 0.1 0.1 0.32

7 0.2 0.9 0.2 0.18 0.1 0.41

9 0.55 0.45 0.45 0.25 0 0.43

11 0.5 0.5 0.5 0.25 0 0.43

12 0.51 0.55 0.51 0.28 0.06 0.47

10 0.9 0.5 0.5 0.45 0.4 0.65

13 0.85 0.77 0.77 0.65 0.62 0.79

14 0.9 0.9 0.9 0.81 0.8 0.9

15 1 1 1 1 1 1

The product t-norm and the γ – operator give us

the same ranking of records except the records 8 and

4. The γ – operator requires double time in

comparison with the product t-norm. On the other

hand, the product t-norm often gives values which

are significantly lower than ones obtained from the

minimum t-norm. For users, it seems that the

compensation of bad and good values is worse than

the bad value. If a user cares about “which objects

does the system get me first” the product t-norm is a

better solution. In other cases, like data examination

in official statistics “how the system does internally

rate its answers” the γ – operator is more

informative. According to results in Table 2, the γ -

operator is the most appropriate one.

Other aggregation operators could be applied,

such as Choquet integral or Ordered Weighted

Averaging (OWA) operators in order to create more

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

256

sophisticated queries. The later one is examined in

(Zadrożny and Kacprzyk, 2009). Prioritized fuzzy

constraint satisfaction problem can be applied in

queries which handle fuzzy conditions. The value

with the biggest priority has the largest impact on

the result given by the priority t-norm (Takači and

Škrbić, 2008).

5 QUERY REALIZATION

In (Bordogna and Psaila, 2008), the following

drawback of fuzzy query languages is recognized:

The proposals defined so far usually assume that

fuzzy predicates are defined “a priori” and included

in a query at need. Even when user-defined fuzzy

predicates can be specified, there are not specific

commands in the query language itself to customize

the meaning of terms. One solution to this issue is

examined in (Tudorie, 2009). The FuzzyKAA is able

to assist a user in defining linguistic terms according

the content in database.

A direct user input is an ideal case (Gurský et al,

2008). It assumes that a user has a clear idea what

data he wants to select. Moreover, it reduces

computational burden. This is often not the case and

a user needs some information about stored values

before he creates query conditions.

5.1 Proposed Interface

In order to manage querying across the approach

examined in sections 3 and 4, the interface for

desktop application depicted in Figure 3 is proposed.

The interface is decomposed into three main parts.

The first part deals with the navigation through a list

of query-able attributes (in this case, adapted to

attributes from the municipal database).

The second part is focused on creation of flexible

query conditions. All chosen attributes for the fuzzy

part of a query are situated inside the tab control.

Each tab page contains one indicator. The user can

directly input parameters of linguistic terms (A, B, C

and D) or ask for the suggestion by one of methods

recommended above (the uniform domain covering

method or the logarithmic transformation).

Third part is devoted to selection of aggregation

function (γ – operator, minimum and Lukasiewicz)

and presenting results in a tabular form.

Finally, the user request is translated into the

SQL query and processed by the database

management system. At the end of this process, the

answer is presented through the interface.

In the suggested approach, users obtain overview

of stored data before a query realization, so they

have a possibility to adjust parameters of fuzzy sets

inside each elementary condition. The suggested

approach could reduce empty answer and

overabundant answer problems. The empty answer

problem simply means that there is no data matching

the overall query condition. The query Q results in

an empty answer if Q(t) = Ø. (Bosc et al, 2008). The

overabundant answer problem is defined as an

answer where the cardinality of Q(t) is too large

(Bosc et al, 2008).

Figure 3: Proposed interface.

6 CONCLUSIONS

Although fuzzy set theory has been already

established as an adequate framework to deal with

flexible queries, there are still many ways how to

improve fuzzy queries. In our paper, we focused on

the issue of fuzzy sets construction and examination

of adequate aggregation functions.

The first issue can be satisfactorily solved if we

merge a user’s opinion about linguistic terms with

the current content in database. A user can directly

input fuzzy sets parameters or ask for suggestions.

The uniform domain coverage method is appropriate

when attribute values are more or less uniformly

distributed inside its domain. In the other case, a

logarithmic transformation is more suitable. This

information helps to reduce empty or overabundant

answer problem.

For the second issue, t-norm functions used in

fuzzy queries are discussed. As a result, the γ –

operator is suggested. This operator takes into

account all membership degrees and compensates a

bad value of one attribute with a good value of

another attribute.

ConstructionofFuzzySetsandApplyingAggregationOperatorsforFuzzyQueries

257

Finally, both above examined issues have been

incorporated into the proposed querying interface.

Integration of approaches of membership

functions construction from current content in

database and selection of appropriate aggregation

operators could bring more sophisticated querying

tool for end users.

The topic for further research is how to recognize

directly from data whether the uniform domain

method is more suitable than the logarithmic

transformation and how to offer most suitable

aggregation operator to meet users' needs.

REFERENCES

Bordogna, G., Psaila, G., 2008. Customizable Flexible

Querying for Classical Relational Databases. In:

Galindo J. (Ed.), Handbook of Research on Fuzzy

Information Processing in Databases (pp. 191-217).

IGI Global, London.

Bosc, P., HadjAli, A., Pivert, O., 2008. Empty versus

overabundant answers to flexible relational queries.

Fuzzy Sets and Systems, 159, 1450-1467.

Bosc, P., Pivert, O., 2000. SQLf query functionality on top

of a regular relational database management system.

In: Pons, M., Vila, M. A., Kacprzyk, J. (Eds.),

Knowledge Management in Fuzzy Databases (pp. 171-

190). Physica-Verlag, Heidelberg.

Branco, A., Evsukoff, A., Ebecken, N., 2005. Generating

fuzzy queries from weighted fuzzy classifier rules, In

ICDM workshop on Computational Intelligence in

Data Mining. IOS Press.

Detyniecki, M., 2001. Fundamentals on Aggregation

Operators, In AGOP International Summer School on

Aggregation Operators. Asturias.

Dubois, D., Prade, H., 1997. Using fuzzy sets in flexible

querying: Why and how? In: Andreasen, T.,

Christiansen, H., Larsen H.L. (Eds.), Flexible Query

Answering Systems (pp. 45-60). Kluwer Academic

Publishers, Dordrecht.

Galindo, J., 2008. Introduction and Trends to Fuzzy Logic

and Fuzzy Databases, In: Galindo J. (Ed.), Handbook

of Research on Fuzzy Information Processing in

Databases (pp. 1-33). IGI Global, London.

Gurský, P., Vaneková, V., Pribolová, J., 2008. Fuzzy User

Preference Model for Top-k Search. In IEEE World

Congress on Computational Intelligence (WCCI).

Hong Kong.

Hudec, M., 2009. An approach to fuzzy database

querying, analysis and realisation. Computer Science

and Information Systems, 6(2), 127-140.

Kacprzyk, J., Zadrożny, S., 2001. Computing with words

in intelligent database querying: standalone and

internet-based applications. Information Sciences, 134,

71–109.

Kacprzyk, J., Zadrożny, S., 1995. FQUERY for Access:

Fuzzy querying for windows-based DBMS, In: Bosc,

P., Kacprzyk, J. (Eds.), Fuzziness in Database

Management Systems (pp, 415-433). Physica-Verlag,

Heidelberg.

Klir, G., Yuan, B., 1995. Fuzzy sets and fuzzy logic, theory

and applications, Prentice Hall. New Jersey.

Meier, A., Werro, N., Albrecht, M., Sarakinos, M. 2005.

Using a Fuzzy Classification Query Language for

Customer Relationship Management. In Conference

on Very Large Data Bases. ACM.

Radojević, D., 2008. Interpolative realization of Boolean

algebra as a consistent frame for gradation and/or

fuzziness, In: Nikravesh, M., Kacprzyk, J., Zadeh,

L.A. (Eds.), Forging New Frontiers: Fuzzy Pioneers II

Studies in Fuzziness and Soft Computing (pp. 295-

318). Springer-Verlag, Berlin and Heidelberg.

Siler, W., Buckley, J., 2005. Fuzzy expert systems and

fuzzy reasoning, John Wiley & Sons. New Jersey.

Takači, A., Škrbić, S., 2008. Priority, Weight and

Threshold in Fuzzy SQL Systems. Acta Polytechnica

Hungarica, 5(1), 59-68.

Tudorie, C., 2008. Qualifying objects in classical

relational database querying, In: Galindo J. (Ed.),

Handbook of Research on Fuzzy Information

Processing in Databases (pp. 218-245). IGI Global,

London.

Tudorie, C., 2009. Intelligent interfaces for database fuzzy

querying, The annals of “Dunarea de Jos” University

of Galati, Fascicle III, 32(2).

Wang, T.C., Lee, H.D., Chen, C.M., 2007. Intelligent

Queries based on Fuzzy Set Theory and SQL. In Joint

Conference on Information Science, World Scientific.

Werro, N., Meier, A., Mezger, C., Schindler, G., 2005.

Concept and Implementation of a Fuzzy Classification

Query Language. In International Conference on Data

Mining. CSREA Press.

Zadeh, L. A., 1965. Fuzzy sets. Information and Control,

8, 338-353.

Zadrożny, S., Kacprzyk, J., 2009. Issues in the practical

use of the OWA operators in fuzzy querying. Journal

of Intelligent Information Systems, 33, 307-325.

Zimmermann, H.-J., 2001. Fuzzy Set Theory – and Its

Applications, Kluwer Academic Publishers. London.

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

258