Prioritization of Product Requirements using

the Analytic Hierarchy Process

Thomas Reichel and Gudula R

unger

Department of Computer Science, Chemnitz University of Technology, 09107 Chemnitz, Germany

Keywords:

Requirements Management, Prioritization, Multi-criteria Decision, Analytic Hierarchy Process.

Abstract:

The prioritization of product requirements is an essential task during the early phases of product development,

which copes with time-to-market deadlines, budgetary constraints, and personnel restrictions. Since several

decision criteria, such as cost, time, and risk, as well as the customer’s point of view and different company

divisions have to be taken into account, the prioritization of requirements corresponds to a multi-criteria,

multi-stakeholder decision problem. In this article, we propose a prioritization approach based on the analytic

hierarchy process (AHP) that creates a ranking of requirements with respect to multiple (maybe conﬂicting)

decision criteria and incorporates assessments of multiple stakeholders. The proposed approach overcomes

the scalability problem of AHP by using hierarchic checklists and an efﬁcient partitioning strategy.

1 INTRODUCTION

The prioritization of product requirements is an es-

sential task during the early phases of product devel-

opment. The priority of a requirement indicates its

importance, urgency, or value for the product to be de-

veloped (Wiegers, 2003; Karlsson and Ryan, 1997).

Prioritization supports the identiﬁcation of key re-

quirements of a product and, thus, helps to recognize

the key issues of product design. To cope with time-

to-market deadlines as well as budgetary and person-

nel restrictions during product development, a careful

prioritization of requirements supports the determina-

tion of valuable requirements which should be imple-

mented in a given product release (Duan et al., 2009).

Moreover, priorities of requirements help to create a

schedule that describes the order in which the require-

ments should be implemented (Pahl et al., 2007).

The point of view of different stakeholders, such

as different company divisions as well as the cus-

tomers and users of a product, should be incorporated

in the prioritization of product requirements (Karls-

son et al., 1997). With a huge number of require-

ments on the one hand and the different stakeholders

on the other hand, the prioritization of requirements is

a complex multi-criteria task that requires collabora-

tion between the stakeholders. To cope with the cog-

nitive limitations of the human mind, insufﬁcient time

for deliberation, limited organizational resources for

information gathering, and related problem-solving

constraints (Janis, 1989), methodological support is

necessary for such multi-criteria, multi-stakeholder

decisions.

To prioritize a huge number of requirements in a

multi-stakeholder environment, we propose a prioriti-

zation approach based on the analytic hierarchy pro-

cess (AHP). The AHP, initially developed by Saaty

(Saaty, 1980), is widely applied in science and in-

dustry and its major use is the resolution of choice

problems in multi-criteria environments (Forman and

Gass, 2001). The beneﬁts of AHP with respect to

other multi-criteria decision making methods is its

ability to incorporate intangibles (Harker, 1987), its

simplicity, ease of understanding, ﬂexibility, and ac-

curacy (Forman and Gass, 2001). Since the traditional

AHP requires a pairwise comparison of all objects

considered (which are the requirements in our case),

the number of comparisons would grow quadratically

with the number of objects.

The contribution of this article is the utilization of

hierarchic checklists to signiﬁcantly reduce the num-

ber of pairwise comparisons in the average case and

hence to overcome the scalability problem of AHP.

The next sections are structured as follows: Sec-

tion 2 presents the background of requirements man-

agement and related prioritization approaches. Sec-

tion 3 describes the AHP in detail and discusses ex-

isting approaches for the reduction of pairwise com-

parisons. The novel prioritization approach proposed

is described in Sect. 4. Finally, Sect. 5 concludes.

Reichel T. and Rünger G..

Prioritization of Product Requirements using the Analytic Hierarchy Process.

DOI: 10.5220/0003969600700076

In Proceedings of the 14th International Conference on Enterprise Information Systems (ICEIS-2012), pages 70-76

ISBN: 978-989-8565-11-2

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

In this section, key issues of the requirements man-

agement in the mechanical and software engineering

domain as well as existing methods and tools for the

prioritization of requirements are described.

2.1 Requirements Management

Design approaches in the mechanical and the software

engineering domain, such as the VDI 2221 guide-

line (VDI, 1993; Pahl et al., 2007), the axiomatic

design (Suh, 2001), and the rational uniﬁed process

(Kruchten, 2003), emphasize an in-depth analysis of

customer needs, a transformation of customer needs

into well-deﬁned product requirements, and ﬁnally

the creation of a product speciﬁcation in the early

stages of the product development process. This pro-

cess is denoted as clariﬁcation (Pahl et al., 2007).

For a prioritization that considers the customer’s

and the manufacturer’s point of view as well as other

factors, such as legal regulations, international guide-

lines, and lately the environmental impact of prod-

ucts, a collaboration between domain experts is nec-

essary. In the mechanical engineering domain, such

a collaboration is denoted as integrated product de-

velopment (Ehrlenspiel, 2009) and plays a major role

for a successful product development project. Be-

sides this human-centered collaboration, Gumienny et

al. (Gumienny et al., 2011) emphasize the necessity

for automated information exchange and information

synthesis between the collaborating experts. There-

fore, an IT-supported prioritization that incorporates

human-centered collaboration as well as information

exchange and synthesis is favourable.

2.2 Requirements Prioritization

For the prioritization of requirements, many ap-

proaches and techniques are used in practice (Duan

et al., 2009). Simple approaches separate re-

quirements into few groups, for example demands

and wishes (Pahl et al., 2007) or functional and

non-functional (qualitative) requirements (Kruchten,

2003), or directly assign weights (important rates) to

customer needs (Ehrlenspiel, 2009). However, these

techniques primarily focus on a coarse categorization

rather than prioritization.

More sophisticated value-oriented methods com-

bine selected factors to calculate a corresponding pri-

ority. For example, Wiegers (Wiegers, 2003) pro-

poses an approach in which the stakeholders rate the

value, the cost, and the technical risk each on a scale

from 1 to 9. The priority of a requirement is then

calculated by

value

(cost + risk)

. In similar approaches,

for example outlined by (Wassermann, 1993) and

(Ehrlenspiel, 2009), the requirements are prioritized

during a quality function deployment (QFD) planning

process, utilizing the expected inﬂuence of customer

needs on requirements in addition to the factors value,

cost, and risk. These value-oriented prioritization ap-

proaches can help to select core requirements (Azar

et al., 2007), but do not consider the collaboration be-

tween stakeholders.

For the prioritization of large sets of requirements,

the BST (binary search tree) is proposed (Ahl, 2005).

The BST is constructed by inserting less important

requirements as left children and more important re-

quirements as right children of a given node in the

BST (similar to the sorting with a BST). Other ap-

proaches for large sets of requirements use automatic

clustering techniques and manual prioritization of

clusters for the prioritization (Duan et al., 2009; Jiang

and Eberlein, 2006). Although these approaches scale

well for large sets of requirements, a major shortcom-

ing is the lower achievable accuracy with respect to

other prioritization approaches.

Several authors suggest the analytic hierarchy pro-

cess (AHP) (Mead, 2008; Karlsson and Ryan, 1997;

Ahl, 2005; Perini et al., 2009; Regnell et al., 2001)

to achieve a consistent, highly accurate, and ratio-

scale prioritization of requirements. Since the tra-

ditional AHP approach is primarily not adapted for

a distributed prioritization with multiple stakeholders

(Regnell et al., 2001), several methods for the incor-

poration of assessments from different stakeholders

are proposed. These include simple median, arith-

metic or geometric mean calculations (Ramanathan,

2001; Saaty, 1980) and the Delphi method (Saaty,

1980; Azani and Khorramshahgol, 1990), which is

an interaction approach between stakeholders to reach

consensus. A key issue of AHP is its lack of scala-

bility, because the prioritization of n requirements re-

quires at least n · (n − 1)/2 pairwise comparisons of

requirements. Several techniques for the reduction

of necessary comparisons have been proposed (see

Sect. 3.2). However, these techniques decrease the

accuracy of the prioritization resulting.

All mentioned prioritization techniques and meth-

ods are utilizable for the relevant issues, i.e., coarse

categorization, assignment of values to requirements,

and fast processing of large sets of requirements. But

they either lack support for collaboration between

stakeholders, accuracy of the prioritization, scalabil-

ity, or considering the multi-criteria environment of

requirements prioritization. The approach for require-

ments prioritization proposed in this article tries to

overcome all these shortcomings by a combination of

PrioritizationofProductRequirementsusingtheAnalyticHierarchyProcess

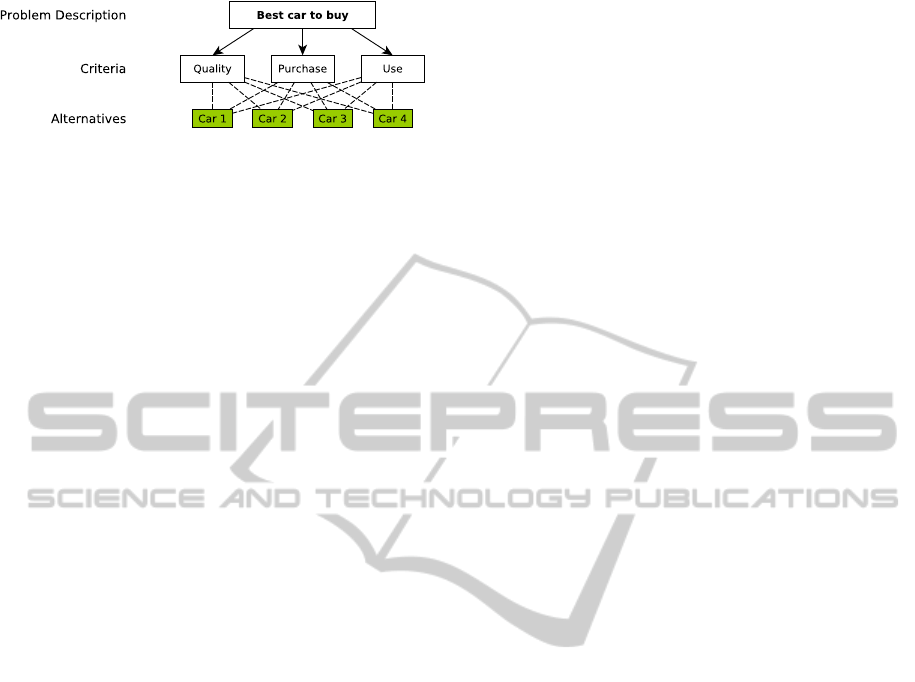
Figure 1: Example AHP criteria hierarchy for an optimal al-

ternative selection, which is choosing the most appropriate

car.

the AHP with aspects of the Delphi method and a new

technique for the reduction of pairwise comparisons.

Since the AHP is essential for this approach, it is sum-

marized in detail in the next section.

3 THE ANALYTIC HIERARCHY

PROCESS

The analytic hierarchy process (AHP), initially pro-

posed by Saaty (Saaty, 1980), is a methodology which

supports multi-criteria decisions in a widespread area

of application, e.g., optimal alternative selection, pri-

oritization, evaluation, or benchmarking (Forman and

Gass, 2001). The AHP enables a calculation of ratio-

scale weights from pairwise comparisons in a multi-

criteria environment. In the following, the major steps

of the AHP are explained in detail and existing ap-

proaches for the reduction of the number of pairwise

comparisons are discussed.

3.1 Steps of AHP

Similar to other approaches for multi-criteria decision

support, the AHP starts with the decomposition of the

problem description into subproblems, followed by

comparative assessments with respect to subproblems

and ends with a synthesis of the assessments. Fig-

ure 1 depicts an example decomposition of a selection

problem and corresponding alternatives. In general,

the AHP can be divided into ﬁve major steps.

1. Problem Decomposition and Creation of a Hi-

erarchy of Criteria. The ﬁrst step of AHP is

the identiﬁcation of the decision criteria of the

overall problem and the creation of a hierarchy of

the criteria. Each criterion may consist of several

sub-criteria. (Azani and Khorramshahgol, 1990)

and (Mendoza and Prabhu, 2009) suggest an inde-

pendent gathering of prospective criteria by each

stakeholder, followed by the creation of the hi-

erarchy in a joint meeting. A careful choice of

stakeholders is essential is this step, including ul-

timately affected (primary) stakeholders as well as

(secondary) stakeholders with intermediary roles.

This ﬁrst step also includes the determination of

possible alternatives.

2. Pairwise Comparisons. After an identiﬁcation of

possible alternatives, the pairwise comparison of

alternatives with respect to criteria on the lowest

level of the hierarchy and the pairwise compari-

son of (sub-)criteria with respect to their superior

criterion in the hierarchy starts. As a result, mul-

tiple quadratic comparison matrices are created.

In the example of Fig. 1, three 4x4 matrices, that

contain the pairwise comparisons of the cars with

respect to the criteria Quality, Purchase and Use,

and one 3x3 matrix, that contains the pairwise

comparisons of Quality, Purchase and Use with

respect to the overall selection problem, are cre-

ated. Each pairwise comparison is rated on an in-

terval scale from 1 (both comparison objects (i.e.,

alternatives or criteria) are equal with respect to

the superior criterion) to 9 (the ﬁrst comparison

object extremely dominates the second object with

respect to the superior criterion). With the recip-

rocal values

,...,1, a lower assessment of the

ﬁrst object can be speciﬁed.

3. Validation of the Consistency of Pairwise Com-

parisons. The rate of consistency is measured by

the consistency ratio CR for each comparison ma-

trix (Saaty, 1980). The CR is calculated based on

the maximal eigenvalue of the matrix. The ratio is

equal to zero for an ideal comparison matrix and

greater than zero for inconsistent matrices. Saaty

proposes a consistency be satisfying, if CR is less

than 0.1.

4. Calculation of Local Weights. For each com-

parison matrix the local weights are calculated. A

local weight speciﬁes the assessment of a compar-

ison object with respect to the superior criterion in

the interval [0,1]. The local weights are deﬁned to

be the values of the ﬁrst eigenvector of the com-

parison matrix which is calculated based on the

maximal eigenvalue of the matrix (Saaty, 1980).

5. Synthesis of Global Weights. The global weights

of alternatives (i.e., the priorities) are calculated

based on the local weights. For each alternative

the local weight of the alternative and the global

weight of the corresponding criterion are multi-

plied. These results are summed for all criteria

on the lowest level of the hierarchy in order to

calculate the global weight of an alternative. The

global weight of a criterion v

on the lowest level

of the hierarchy is calculated by multiplying the

local weights of the criteria on the path between

and the overall problem description (i.e., the

root of the hierarchy).

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

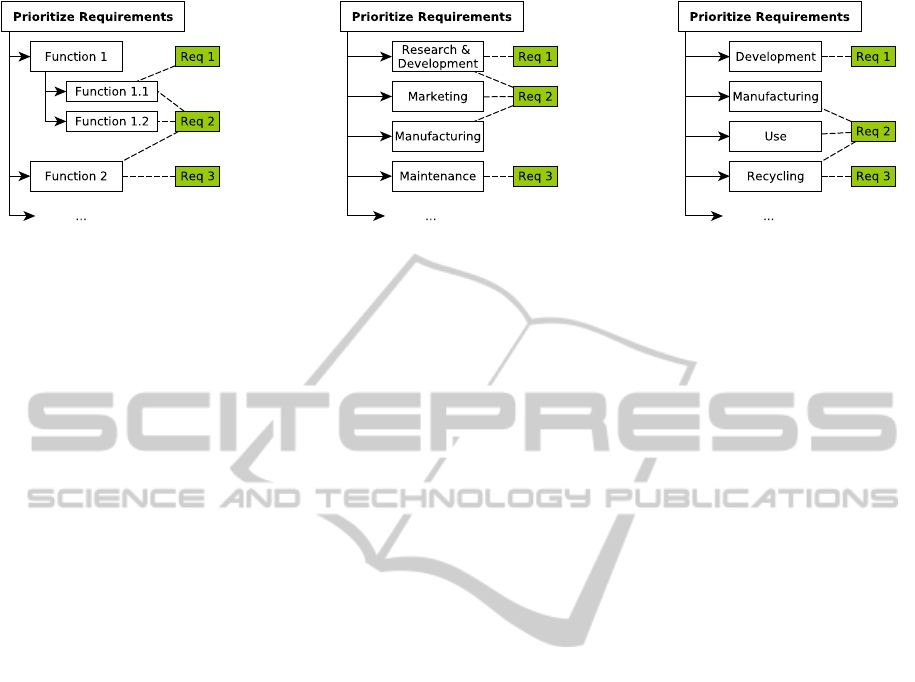
Figure 2: Examples for organizing requirements in hierarchical form. Left: Assignment to functionalities. Middle: Assign-

ment to responsible company departments. Right: Assignment to life cycle phases.

3.2 Existing Approaches for the

Reduction of Pairwise Comparisons

Wedley et al. (Wedley et al., 1993) states that there

are only n − 1 comparisons necessary for the calcu-

lation of the local weights of n comparison objects.

The remaining comparisons are derived from the n−1

comparisons. Based on a case study, the authors rec-

ommend to compare all objects with the object with

the lowest (assumed) rank to achieve the minimum

inconsistency.

Since redundant comparisons are necessary to

check the assessments and to measure the consistency,

Harker (Harker, 1987) proposes so-called local stop-

ping rules. These rules require further comparisons

(beyond Wedleys n − 1 comparisons) only if a next

comparison can signiﬁcantly contribute to the cur-

rent local weights. An extension of this approach,

described by Millet and Harker (Millet and Harker,

1990), introduces so-called global stopping rules that

take the entire decision hierarchy into account. Com-

parisons of a speciﬁc branch in the criteria hierarchy

are performed only if the entire branch signiﬁcantly

contributes to the global weights of the alternatives.

Another (local) approach is proposed by Shen et

al. (Shen et al., 1992) who suggest the partitioning

of the set of comparison objects into groups which

have one comparison object in common. While the

weights of the comparison objects in the groups are

determined with the traditional approach, the weights

for the entire set are directly derived from the group

weights and the weight of the common object.

Weiss and Rao (Weiss and Rao, 1987) propose

the so-called use of incomplete experimental design

in which each stakeholder compares a subset of the

hierarchy only and, thus, the number of comparisons

is reduced for each stakeholder. The authors also sug-

gest the deletion of certain attributes in order to re-

duce the size of the AHP hierarchy a priori.

The approaches mentioned reduce the number of

comparisons in arbitrary AHP decision problems and

accept a minimum increase of inconsistency. In con-

trast, the approach for the reduction of pairwise com-

parisons proposed in this article tries to preserve the

accuracy of the global weights. Furthermore, the

approach proposed can be combined with the ap-

proaches outlined in this section.

4 AHP APPROACH FOR THE

PRIORITIZATION OF

REQUIREMENTS

The requirements prioritization approach proposed in

this section utilizes the AHP to incorporate multiple

criteria and multiple stakeholders for the prioritiza-

tion of requirements. The approach provides tech-

niques for the effective reduction of necessary pair-

wise comparisons of requirements based on the hier-

archic structuring and partitioning of requirements.

4.1 Hierarchic Structuring of

Requirements

A partitioning of requirements into groups with sim-

ilar concerns is often used to manage a huge number

of requirements. As described by (Pahl et al., 2007;

Ehrlenspiel, 2009; Kruchten, 2003), tree structures

are appropriate for such a partitioning. A partitioning

according to the major functionalities of the product

(Fig. 2, left) is frequently used, because functionali-

ties can (hopefully) be developed independently and

integrated afterwards (for example speciﬁed by the

V-model (Boehm, 1979; VDI, 2004)). Pahl/Beitz

(Pahl et al., 2007) propose so-called partial require-

ments lists that contains requirements related to dif-

ferent company departments (Fig. 2, middle). Since

life cycle oriented development becomes mandatory

for technical products, also a partitioning into life cy-

cle phases can be helpful to structure requirements

(Fig. 2, right). Because of cross-cutting concerns,

PrioritizationofProductRequirementsusingtheAnalyticHierarchyProcess

requirements may belong to more than one concern

and, thus, should be part of several groups of require-

ments (e.g., Req 2 in Fig. 2). For example, the require-

ment ”increase energy efﬁciency”, may belong to the

life cycle phases manufacturing, use, and recycling as

well as to several company departments, such as mar-

keting, management, and Research & Development.

Ehrlenspiel (Ehrlenspiel, 2009) and Pahl/Beitz

(Pahl et al., 2007) incorporate life cycle, organiza-

tional, and functional aspects of product requirements

in order to create a hierarchic structure. These check-

lists contain general aspects of a product to be devel-

oped and can be used to validate the completeness of

a requirements speciﬁcation as described in (Reichel

et al., 2011).

For the requirements prioritization with AHP, we

propose to use checklists to efﬁciently reduce the

number of pairwise comparisons by utilizing the tree

structure of the checklist as criteria hierarchy (step 1

of the AHP). For each criterion on the lowest level of

the hierarchy, only the requirements that are directly

related to the criterion are rated (step 2 of the AHP).

The local weights of the requirements that are not re-

lated to the criterion are assumed to be zero. This as-

sumption is reasonable, since all requirements that are

not related to a criterion should be prioritized as low

as possible when only this criterion is considered. The

modiﬁed assignment of alternatives to criteria on the

lowest level of the hierarchy extends the conventional

AHP approach with the goal to reduce the number of

pairwise comparisons while preserving the accuracy

of the priorities resulting.

4.2 Prioritization of Requirements

The prioritization of requirements start with the de-

termination of a criteria hierarchy as described in

Sect. 3.1 (step 1) in order to decompose the overall

prioritization problem. The prioritization utilizes a

checklist described in Sect. 4.1 as criteria hierarchy,

since it provides the necessary problem decomposi-

tion. If such a checklist is already used for the pre-

ceding clariﬁcation of requirements, as proposed in

(Reichel et al., 2011), the reuse of the checklist for the

prioritization is beneﬁcial, especially because the hi-

erarchic structure of the checklist (i.e., the criteria hi-

erarchy) is determined by all stakeholders concerned

and the product requirements are already assigned to

the corresponding checklist items (i.e., criteria).

If a checklist is not used in the requirements clari-

ﬁcation so far, it has to be created by all stakehold-

ers concerned. The creation process of a checklist

highly depends on the product type and the num-

ber of stakeholders involved. For a small number of

stakeholders, an informal meeting can be sufﬁcient

to create the criteria hierarchy. However, for large

groups a methodological approach, such as the Del-

phi Method (Azani and Khorramshahgol, 1990) or a

value-based multi-stakeholder approach as described

by (Mendoza and Prabhu, 2009), is recommendable

to obtain the point of view of all stakeholders. After

the creation of the criteria hierarchy, all requirements

have to be assigned to corresponding (sub-)criteria.

With a huge number of requirements to be assigned it

is feasible that the stakeholders assign subsets of the

requirements simultaneously. Since the assignments

have a strong impact of the priorities resulting, all as-

signments should be reviewed by other stakeholders.

In the next step of the prioritization, pairs of re-

quirements and pairs of criteria are compared. This

step starts with the pairwise comparison of require-

ments with respect to the criteria of the lowest level,

followed by the pairwise comparison of criteria with

respect to their superior criterion. As proposed by

(Forman and Gass, 2001; Schoner and Wedley, 1989),

this bottom-up approach should be used if the in-

dependence of requirements and higher-level criteria

could not be assured, i.e., the weighting of higher-

level criteria depends on the given requirements.

In order to limit the number of pairwise compar-

isons for each stakeholder on the one hand and to

achieve a high accuracy of the prioritization on the

other hand, two strategies are used for the compar-

isons.

1. Partitioning. In the partitioning strategy, differ-

ent groups of stakeholders compare different sets

of requirements with each other. The strategy is

primarily used to reduce the number of compar-

isons for individual stakeholders and to transfer

pair comparisons of requirements of a similar do-

main to the corresponding domain experts. The

partitioning strategy may decrease the accuracy

of the prioritization, since not all stakeholders are

involved in the comparison of all requirements.

However, a pairwise comparison of requirements

related to a speciﬁc domain by an expert not fa-

miliar with the domain may also decrease the ac-

curacy. This strategy corresponds to the use of in-

complete experimental design by Weiss and Rao

(Weiss and Rao, 1987) for the prioritization of re-

quirements.

2. Consensus. In the consensus strategy, a group of

stakeholders (e.g., experts of different domains)

assess the same set of requirements (or criteria)

independently. For this well-known strategy, we

propose to use the following indicators to deter-

mine a signiﬁcant deviation of stakeholder com-

parisons.

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems

(a) The pairwise comparisons of two stakehold-

ers result in different orders (ranks) of the local

weights of the compared objects;

(b) The euclidean distance of the local weight

vector of the criterion is above a user-deﬁned

limit;

viation of stakeholder comparisons has a sig-

niﬁcant inﬂuence of the priorities resulting (the

sensitivity analysis in AHP determines the in-

ﬂuence of single pairwise comparisons on the

global weights).

While the indicators (a) and (b) can be calculated

based on the given local weights, the indicator (c)

requires pairwise comparisons for the entire hier-

archy to calculate the priorities resulting.

The independent comparisons are either uniﬁed

using the geometric mean proposed by (Mc-

Carthy, 1992) or, if the indicators exceeds a user-

deﬁned limit, an additional interaction between

the stakeholders to achieve consensus for the par-

ticular comparisons is necessary. This strategy is

primarily applied to consolidate the accuracy of

the prioritization with respect to all stakeholders.

We propose the usage of the partitioning strat-

egy for the comparison of requirements by the cor-

responding domain experts. Therefore, the task of

pairwise comparisons of requirements with respect to

criteria on the lowest level is distributed among the

domain experts. The following pairwise comparisons

of criteria with respect to the corresponding higher-

level criteria is done by using the consensus strategy.

After the completion of the pairwise comparisons,

a consistency check, according to step 3 of the AHP,

validates the consistency of the comparisons. If an

inconsistency is found (i.e., a consistency ratio above

0.1), the comparisons have to be revised by the cor-

responding stakeholder. The comparison matrices

which are created with a consensus strategy by differ-

ent stakeholders have to be uniﬁed as described in the

consensus strategy. An exceeding deviation not nec-

essarily implies that the geometric mean of dissonant

comparison matrices is not sufﬁcient for the uniﬁca-

tion of the matrices, but the corresponding stakehold-

ers should be aware of deviant comparisons and be

potentially able to correct the comparisons.

The ﬁnal steps of the requirements prioritization

are the determination of local and global weights

(steps 4 and 5 of the AHP). According to Sect. 4.1, the

local weights of requirements with respect to criteria

on the lowest level of the hierarchy are determined by

calculating the eigenvector of the corresponding com-

parison matrix for related requirements and by assum-

ing a weight of zero for unrelated requirements. The

eigenvector method is also used for the determination

of all local weights of criteria with respect to their

higher-level criterion. Based on the local weights the

global weights, i.e., the priorities of the requirements

are determined as described in Sect. 3.1.

When requirements are modiﬁed after the comple-

tion of the prioritization, the corresponding compari-

son matrices have to be revised by the stakeholders

assigned. If the modiﬁcation of requirements also af-

fects the assessment of related criteria, the compari-

son matrices of the superior criteria have to be revised

additionally.

The determination of the criteria hierarchy as well

as the determination of the relations between require-

ments and the criteria on the lowest level of the hi-

erarchy are the crucial decisions for the achievement

of valid priorities. Therefore it is arguable whether a

checklist hierarchy utilized during the clariﬁcation of

requirements (as described in Sect. 4.1) can always be

applied for the requirements prioritization. An adap-

tion of the hierarchy may be necessary. However, the

relations between requirements and checklist items

(i.e., criteria) created in the clariﬁcation are highly

consistent, since the relations are already utilized to

validate the completeness of requirements speciﬁca-

tions (Reichel et al., 2011).

5 CONCLUSIONS

The approach for the prioritization of requirements

proposed in this article utilizes the analytic hierarchy

process (AHP) for an efﬁcient and precise determina-

tion of priorities. The overall prioritization problem

is decomposed into subproblems that require the pair-

wise comparison of requirements with respect to sin-

gle decision criteria of the overall problem. Due to

this decomposition, multiple domain experts can par-

ticipate in the process, either by weighting require-

ments and criteria of their own domain only or by

weighting requirements and criteria in a corporate de-

cision to achieve consensus. We propose several in-

dicators for the determination of a signiﬁcant devia-

tion of expert assessments. In addition to both strate-

gies for the incorporation of experts, an approach for

the reduction of necessary pairwise comparisons of

requirements is proposed. The reduction approach is

based on the assumption that local weights are equal

to zero for requirements which are not related to cri-

teria on the lowest level of the AHP hierarchy. The

prioritization approach proposed improves the scala-

bility of the AHP and, thus, can be applied for the pri-

oritization of medium and large sets of requirements.

PrioritizationofProductRequirementsusingtheAnalyticHierarchyProcess

ACKNOWLEDGEMENTS

The Cluster of Excellence “Energy-Efﬁcient Prod-

uct and Process Innovation in Production Engineer-

ing” (eniPROD

) is funded by the European Union

(European Regional Development Fund) and the Free

State of Saxony.

REFERENCES

Ahl, V. (2005). An experimental comparison of ﬁve priori-

tization methods - investigating ease of use, accuracy

and scalability. Master’s thesis, Blekinge Institute of

Technology, Ronneby, Sweden.

Azani, H. and Khorramshahgol, R. (1990). Analytic Delphi

Method (ADM): A strategic decision making model

applied to location planning. Engineering Costs and

Production Economics, 20(1):23 – 28.

Azar, J., Smith, R., and Cordes, D. (2007). Value-oriented

requirements prioritization in a small development or-

ganization. Software, IEEE, 24(1):32 –37.

Boehm, B. (1979). Guidelines for verifying and validating

software requirements and design speciﬁcations. In

Proc. of European Conf. of Applied Information Tech-

nology, pages 711–719.

Duan, C., Laurent, P., Cleland-Huang, J., and Kwiatkowski,

C. (2009). Towards automated requirements pri-

oritization and triage. Requirements Engineering,

14(2):73–89.

Ehrlenspiel, K. (2009). Integrierte Produktentwick-

lung. Denkabl

aufe, Methodeneinsatz, Zusammenar-

beit. Hanser Fachbuch, 4th edition.

Forman, E. and Gass, S. (2001). The analytic hierarchy pro-

cess - an exposition. Operations Research, 49(4):469–

486.

Gumienny, R., Lindberg, T., and Meinel, C. (2011). Explor-

ing the synthesis of information in design processes -

opening the black-box. In Proc. of the 18th Int. Conf.

on Engineering Design (ICED2011), pages 446–455.

Harker, P. T. (1987). Incomplete pairwise comparisons in

the analytic hierarchy process. Mathematical Mod-

elling, 9(11):837 – 848.

Janis, I. (1989). Crucial Decisions: Leadership in Policy-

making and Crisis Management. Free Press.

Jiang, L. and Eberlein, A. (2006). Analysis of require-

ments engineering techniques using clustering. In

Proc. of the 13th IEEE Int. Conf. on the Engineering

of Computer-Based Systems (ECBS 2006).

Karlsson, J., Olsson, S., and Ryan, K. (1997). Improved

practical support for large-scale requirements priori-

tising. Requirements Engineering, 2(1):51–60.

Karlsson, J. and Ryan, K. (1997). A cost-value approach for

prioritizing requirements. Software, IEEE, 14(5):67–

74.

Kruchten, P. (2003). Rational Uniﬁed Process: An Intro-

duction. Addison-Wesley Longman, Amsterdam.

McCarthy, K. (1992). Comment on the analytic del-

phi method. Int. Journal of Production Economics,

27(2):135–136.

Mead, N. (2008). Requirements prioritization introduction.

Technical report, Carnegie Mellon University, Soft-

ware Engineering Institute.

Mendoza, G. and Prabhu, R. (2009). Evaluating multi-

stakeholder perceptions of project impacts: a partic-

ipatory value-based multi-criteria approach. Int. Jour-

nal of Sustainable Development & World Ecology,

16(3):177–190.

Millet, I. and Harker, P. (1990). Globally effective ques-

tioning in the analytic hierarchy process. European

Journal of Operational Research, 48(1):88 – 97.

Pahl, G., Beitz, W., Feldhusen, J., and Grote, K.-H. (2007).

Engineering Design. A Systematic Approach. Springer

London.

Perini, A., Ricca, F., and Susi, A. (2009). Tool-supported

requirements prioritization: Comparing the AHP and

CBRank methods. Information and Software Technol-

ogy, 51(6):1021 – 1032.

Ramanathan, R. (2001). A note on the use of the analytic hi-

erarchy process for environmental impact assessment.

Environmental Management, 63(1):27 – 35.

Regnell, B., Hst, M., och Dag, J., Beremark, P., and Hjelm,

T. (2001). An industrial case study on distributed pri-

oritisation in market-driven requirements engineering

for packaged software. Requirements Engineering,

6(1):51–62.

Reichel, T., R

unger, G., Steger, D., and Xu, H. (2011). IT

support for the creation and validation of requirements

speciﬁcations - with a case study for energy efﬁciency.

In Proc. of the 18th Int. Conf. on Engineering Design

(ICED2011), volume 10, pages 167–177.

Saaty, T. (1980). The Analytic Hierarchy Process. McGraw-

Hill, New York.

Schoner, B. and Wedley, W. (1989). Ambiguous criteria

weights in AHP: consequences and solutions. Deci-

sion Sciences, 20(3):462–475.

Shen, Y., Hoerl, A., and McConnell, W. (1992). An incom-

plete design in the analytic hierarchy process. Mathe-

matical and Computer Modelling, 16(5):121 – 129.

Suh, P. (2001). Axiomatic Design. Advances and Applica-

tions. Oxford University Press, New York.

VDI (1993). VDI 2221 - Systematic approach to the devel-

opment and design of technical systems and products.

Beuth Verlag Berlin.

VDI (2004). VDI 2206, Design methodology for mecha-

tronic systems. Beuth Verlag Berlin.

Wassermann, G. (1993). On how to prioritize design re-

quirements during the QFD planning process. IIE

Transactions, 25(3):59–65.

Wedley, W., Schoner, B., and Tang, T. (1993). Starting

rules for incomplete comparisons in the analytic hi-

erarchy process. Mathematical and Computer Mod-

elling, 17(4-5):93 – 100.

Weiss, E. and Rao, V. (1987). AHP design issues for large-

scale systems. Decision Sciences, 18(1):43–57.

Wiegers, K. (2003). Software Requirements. Microsoft

Press, 2nd edition.

ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems