
FDMM: A Formalism for Describing ADOxx Meta Models and Models
Hans-Georg Fill
1
, Timothy Redmond
2
and Dimitris Karagiannis
1
1
Research Group Knowledge Engineering, University of Vienna, Vienna, Austria
2
Stanford Center for Biomedical Informatics Research, Stanford University, Stanford, U.S.A.
Keywords:
Conceptual Modeling, Meta Modeling, Domain-specific Modeling.
Abstract:
In the paper at hand we present the FDMM formalism that can be used to describe the core constituents of
the ADOxx meta modeling approach as it is provided for the Open Models Initiative (OMI). The formalism is
based on a first-order logic setting. Thereby formal descriptions of the implementation of modeling languages
based on ADOxx can be realized in an intuitive and mathematically exact format. To illustrate the use of
the formalism it is applied to a modeling language and its instances from the area of risk management that
has been previously implemented in ADOxx. It is then analysed how the concepts of the FDMM formalism
compare to the ADOxx meta modeling concepts as well as other meta modeling approaches from the area of
domain-specific modeling.
1 INTRODUCTION
Conceptual models are today used in many areas
of enterprise information systems (Kaschek, 2008;
Karagiannis et al., 2008a; Wand and Weber, 2002).
Examples range from fields such as strategic man-
agement, business process and workflow manage-
ment to enterprise architecture and software engineer-
ing. For these purposes a large variety of modeling
languages have been developed and successfully ap-
plied in academia and industry (Borgida et al., 2009).
When it comes to the sharing of such modeling lan-
guages and their corresponding models - as it has
been recently promoted by the Open Models Intia-
tive (Koch et al., 2006; Karagiannis et al., 2008b)
- the exact description of a modeling language and
the models is one of the most important tasks. These
descriptions not only reflect the design choices made
during the implementation of the language. They also
permit to compare and learn from different implemen-
tations of a modeling language and support the inter-
pretation of the models (Hinkelmann et al., 2010).
In order to describe the building blocks of mod-
eling languages it can be reverted to several types of
meta modeling approaches (Kern et al., 2011). These
approaches provide the constructs necessary for de-
scribing the abstract and concrete syntax of a mod-
eling language (Harel and Rumpe, 2004; Karagian-
nis and Kuehn, 2002). In this way they also de-
fine constraints and correctness criteria for creating
valid models based on the definition of a modeling
language. In the context of the Open Models Initia-
tive, several projects
1
have reverted to the freely avail-
able and industry proven ADOxx
2
meta modeling ap-
proach. At its core, the ADOxx approach allows to
specify the syntax of a modeling language together
with its graphical representation. From these speci-
fications, visual model editors are then created auto-
matically (Kuehn, 2010).
For the description of ADOxx based modeling
languages, it has so far either been reverted to natural
language descriptions, e.g. (Bork and Sinz, 2010; Fill
et al., 2007), concrete implementations in the form
of source code, e.g. (Schwab et al., 2010; Nemetz,
2006) or visual representations, e.g. (Hofer, 2011;
Braun and Winter, 2005). A formal description of the
ADOxx meta modeling approach is so far not avail-
able. This is however necessary to analyze and eval-
uate how the syntax of a certain modeling language
has been realized, compare ADOxx meta models and
models to other meta modeling approaches such as
GME, Ecore or ARIS cf. (Kern et al., 2011), derive
suggestions for its enhancement and finally describe
semantics for its further processing (Demirkan et al.,
2008; Harel and Rumpe, 2004).
Therefore we propose the FDMM
3
formalism that
1
See http://www.openmodels.at/web/omi/omp
2
ADOxx is a registered trademark of BOC AG.
3
The acronym FDMM stems from: A Formalism for
133
Fill H., Redmond T. and Karagiannis D..
FDMM: A Formalism for Describing ADOxx Meta Models and Models.
DOI: 10.5220/0003971201330144
In Proceedings of the 14th International Conference on Enterprise Information Systems (ICEIS-2012), pages 133-144
ISBN: 978-989-8565-12-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
is capable of describing the core constitutents of the
ADOxx approach. FDMM aims to provide an easy to
use formalism that does not require specialized math-
ematical knowledge and that is capable of expressing
the implementation of ADOxx meta models and mod-
els. The paper is structured as follows: In section 2
we will briefly discuss the foundations of modeling
languages, meta models and models, the characteris-
tics of the ADOxx approach and describe a running
example for a modeling language from the area of en-
terprise information systems. Section 3 will describe
the formalism including the necessary constraints and
correctness criteria. In section 4 the formalism will
be applied to the sample modeling language. The re-
sult of this application is then discussed in section 5.
Work related to the approach will be part of section 6.
The paper is concluded by an outlook on the future
work in section 7.
2 FOUNDATIONS
In this section we will briefly define the terms mod-
eling language, meta model and model and describe
the main characteristics of the ADOxx meta modeling
approach. Finally, we will present a running example
by using a modeling language from the area of risk
management.
2.1 Modeling Language, Meta Model
and Model
According to a framework proposed by (Karagiannis
and Kuehn, 2002), a modeling language is composed
of a syntax, semantics and notation. The syntax spec-
ifies the elements and attributes of the language and
the semantics assigns meaning to these constructs. In
contrast to other frameworks, the notation is treated
separately and is used to specify the visual represen-
tation of the language. The syntax further consists
of an abstract syntax, which is represented by the
meta model, and the concrete syntax, which is rep-
resented by a model (Harel and Rumpe, 2000; Harel
and Rumpe, 2004; Sprinkle et al., 2010). The meta
model can itself be described by a modeling language,
i.e. the meta modeling language. Accordingly, the ab-
stract syntax of the meta modeling language is repre-
sented by a meta meta model and the concrete syntax
is represented by a meta model (Kern et al., 2011).
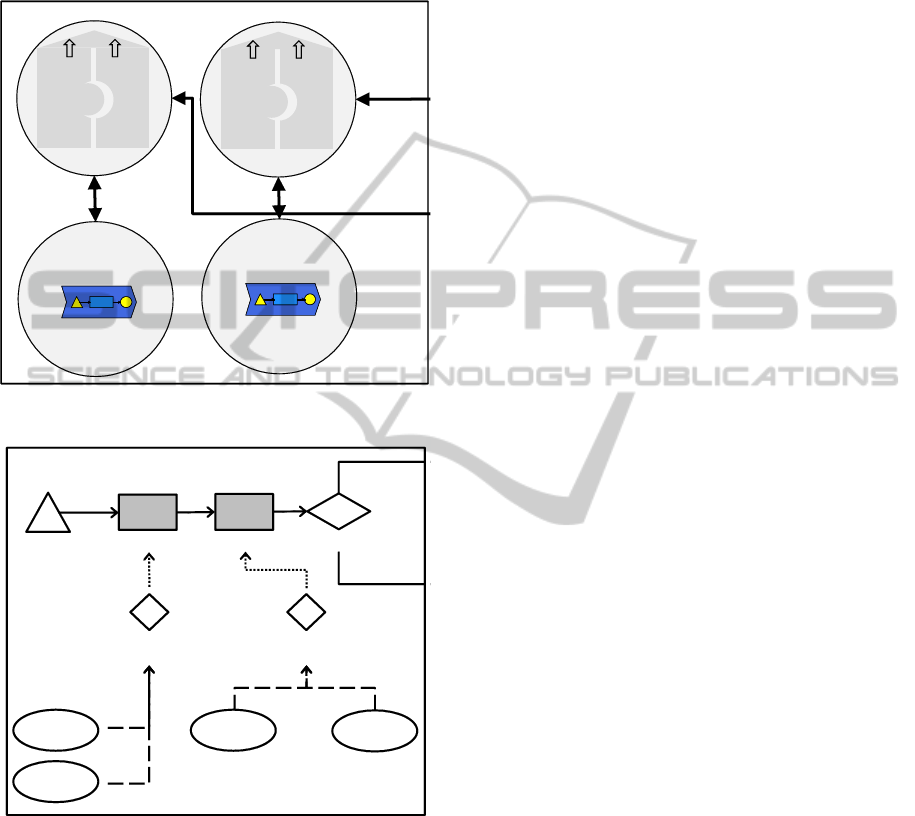
An example for these relationships is shown in fig-
ure 1: in the meta meta model the two entities element
Describing ADOxx Meta Models and Models
and attribute are defined. Additionally, a relation be-
tween the two entities is shown. On the meta model
level the E
1
entity is defined as an element and the A
1
and A
2
entities as attributes that can be related to E
1
.
Finally, on the model level the entities ε
1
and ε
2
are
defined as E
1
elements, the α
1
and α
2
entities as A
1
attributes and the β
1
and β
2
entities as A
2
attributes.
The meta meta model thus defines which entities are
provided for the specification of the abstract syntax
of a modeling language in the form of a meta model.
If the specification of the meta meta model is generic
enough it can be used to specify a multitude of differ-
ent modeling languages. A typical use case is then to
automatically create model editors based on the static
meta meta model specification and the dynamically
adaptable meta model specifications.
Element Attribute
E
1
A
1
A
2
ε
1
ε
2
α
1
α
2
β
1
β
2
Model
Meta
Model
Meta
Meta
Model
is-a
attached-to
Figure 1: Example for a Meta Meta Model, a Meta Model
and a Model.
In addition to association mechanisms for defin-
ing linkages between entities, meta meta models typi-
cally also provide inheritance and containment mech-
anisms (Sprinkle et al., 2010). By inheritance mecha-
nisms, generalization and specialization relationships
between entities of a meta model can be expressed
to provide means for effecting polymorphic behaviors
at model execution or interpretation time. This is re-
quired in particular for the design of algorithms that
shall work on multiple, similar modeling languages
without the need of particular adaptations: by defin-
ing an algorithm on a set of general entities that are
shared by different meta models, the algorithm can be
later bound automatically to entities that are inherited
from these general entities. Containment mechanisms
refer to the inclusion of a set of entities into another
entity on the model level. This is typically used to
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
134

specify model/diagram types or aggregations/nestings
that group sets of entities.
2.2 The ADOxx Meta Modeling
Approach
The ADOxx meta modeling approach has origi-
nally been conceived in the course of the develop-
ment of the ADONIS business process management
toolkit in 1995. Since then it has been successfully
used in a large number of academic and commer-
cial projects by more than 1000 customers world-
wide (Harmon, 2010; Junginger et al., 2000). The ba-
sic building blocks of its meta meta model are classes
and relationclasses that are complemented with at-
tributes (Junginger et al., 2000). Classes are orga-
nized in the form of an inheritance hierarchy so that
the attributes of a super-class are inherited by its sub-
classes in the sense of standard object orientation
principles. Relationclasses are defined by their from-
class and to-class attributes to specify valid instances
of source and target classes. These relations can be
complemented with cardinality constraints to limit the
number of participating instances.
For collections of classes and relationclasses a
containment mechanism in the form of model types is
available. Model types define the context for the in-
stantiation of classes and relationclasses in the form
of models. Therefore, when creating a model, at
first a model type has to be selected to specify which
classes and relationclasses are valid in a model. Sub-
sequently, these classes and relationclasses are instan-
tiated as part of the model.
Besides the standard data types such as integer,
string, and double, enumeration attributes are avail-
able in ADOxx that contain pre-defined values that
can only be selected but not modified by a user during
modeling. Furthermore, attributes can also be of two
special types: attributes of the type expression con-
tain strings in a proprietary expression grammar for
automatically calculating the value of an attribute. At-
tributes of the type interref allow linking the instance
of a class to another class instance of the same or of
a different model instance or linking it to the same or
a different model instance itself. The graphical rep-
resentation of the instances of classes and relation-
classes is specified via the particular string attribute
named GRAPHREP. This attribute permits to specify
context-dependent graphical representations for the
classes and relationclasses, again based on a propri-
etary grammar - cf. (Fill, 2009). Although an inherent
part of the ADOxx approach, the graphical represen-
tation can thus be modified independently from the
other entities.
With these characteristics, the following require-
ments were defined for a formalism that can describe
the concepts of the ADOxx meta modeling approach:
It should permit a formal description of the approach
that is easy to handle and thus suitable for a wide
range of users. Therefore, the formalism should fo-
cus on the core constituents to enable the description
of arbitrary modeling languages that have been imple-
mented using the ADOxx approach. It should how-
ever be extensible to allow its further development
and future refinement.
2.3 Running Example: The 4R
Modeling Language
As a running example we will revert to an existing
modeling language in enterprise information systems
from the area of governance, risk, and compliance
(GRC). This example will first illustrate how meta
models and models are typically used in information
systems to create domain conceptualizations. In sec-
tion 4 we will revert to it again for showing the appli-
cation of the FDMM formalism.
In the last years particular consideration has been
given to the management of risks and regulatory com-
pliance together with their effects on returns and cor-
responding reporting requirements of enterprises. In
line with these developments, the framework for inte-
grated enterprise balancing has been derived (Faisst
and Buhl, 2005; Fill et al., 2007; Gericke et al., 2009).
The goal of this framework is to govern business ac-
tivities with organization-wide consistent return and
risk indicators. As a foundation, it is necessary to
provide a common data basis that represents infor-
mation from the areas of risk, return, regulation, and
reporting - the so-called 4R information architecture.
For acquiring this information, the 4R modeling lan-
guage (Fill et al., 2007) and the 4R situational method
for implementing such solutions in an organization
were developed (Gericke et al., 2009). In its origi-
nal form, the central parts of the 4R modeling lan-
guage were illustrated by an extension of a graph
based formalism. The corresponding realization us-
ing the ADOxx meta modeling approach was however
described in natural language.
The meta model of the 4R modeling language,
as it was specified in ADOxx, contains the follow-
ing model types (Fill et al., 2007): the 4R portfolio
model, the 4R business process model, and the 4R or-
ganizational model. Briefly summarized, the portfo-
lio model type is used to describe multi-dimensional
aggregations of the risks, returns and correlations
of business transactions in regard to their relations
to products and customers (Faisst and Buhl, 2005).
FDMM:AFormalismforDescribingADOxxMetaModelsandModels
135

The single business transactions in this model can be
linked to instances of the 4R business process model
type. This second model type extends the process
modeling language of business graphs (Karagiannis
et al., 1996) with elements, relations, and attributes
for representing events, aggregations of events and
their influence on the properties of process activties.
The meta model is complemented with a 4R organi-
zational model for representing actors, organizational
units, resources, and roles that fulfill tasks in a busi-
ness process.
For the implementation of the 4R model types on
ADOxx the following classes and relationclasses to-
gether with several attributes were specified to rep-
resent the risk and return figures of business transac-
tions and the underlying risk-affected business pro-
cesses:
• for the portfolio model type the class business
transaction and the relationclass relates business
transaction,
• for the 4R business process model the super class
FlowObject and as sub classes of this class: Start,
Decision, SubProcess, Activity, Parallelity, Join,
and End. Additionally the classes: 4R risk aggre-
gation, and 4R event; the relationclasses: subse-
quent, 4R aggregation relation, and 4R influences
relation
• for the 4R organizational model the classes: ac-
tor, organizational unit, resource, and role; and
the relationclasses: uses resouce, belongs to unit,
has role, and has resource
To apply the FDMM formalism we will later re-
gard the 4R portfolio model and the 4R business pro-
cess model type in more detail. The classes and re-
lationclasses of these model types are represented by
the sets of symbols as shown in figure 2.
3 THE FDMM FORMALISM
As stated in the introduction, the goal of this paper
is to develop a formalism that is capable of describ-
ing the core constituents of ADOxx meta models and
models as well as the criteria for valid models based
on the meta model definitions. FDMM is therefore
not a formalization of all aspects of the ADOxx ap-
proach, but a formalism that aims to support users of
ADOxx to describe their meta models and models in a
formal way. For the development of the formalism we
reverted both to literature sources on the ADOxx meta
modeling approach as well as existing implementa-
tions (Karagiannis et al., 2008a; Fill, 2009; Kuehn,
2010). During the development we aimed for keeping
W:
RE:
RI:
WE:
RE:
RI:
BP Model
Business Transaction
[Aggregated view]
W: value; RE: return; RI: risk
Business Transaction
[Single view]
WE: value; RE: return; RI: risk
Relates business
transaction
ρ: correlation
between business
transactions
ρ:
Start
Decision
Activity
Parallelity
Join
End
4R risk
aggregation
4R event
subsequent
4R influences
relation
ʌ
4R aggregation relation
ε: probability of occurrence;
I: estimated impact
ε= I=
Figure 2: Symbols of the 4R Portfolio Model Type and the
4R Business Process Model Type.
the formalism as simple as possible while not sacri-
ficing any of the core concepts of the approach.
3.1 Definition of Meta Models
At first we define the basic constituents of meta mod-
els MM which can then be used to derive model in-
stances mt. We define a meta-model to be a tuple of
the form
MM =
MT, , domain, range, card
(1)
where
• MT is the set of model types. We have
MT =
{
MT
1
, MT
2
, . . . , MT
m
}
(2)
where MT
i
in turn is a tuple,
MT
i
=
O
T
i
, D
T
i
, A
i
(3)
consisting of the set of object types O
T
i
, a set of
data types D
T
i
, and a set of attributes A
i
. In this
way ADOxx classes and relationclasses are uni-
formly represented as object types. As will be de-
scribed below we will use the attributes A
i
also
for expressing associations between object types.
When we describe the instantiation of the meta
model in section 3.2 in model instances, the at-
tributes will map the instantiation of object types
to the instantiation of either object types or data
types. This permits us to represent the ADOxx
concepts of relationclasses and interref relations
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
136

in the same way. However, this also means that,
if for example directed relations are required, the
notions of source and target object types have
to be added when specifying a particular meta
model. The object types, data types, and attributes
are part of their respective total sets:
O
T
=
[
j
O
T
j
, D
T
=
[
D
T
i
, A =
[
A
i
(4)
• is an ordering on the set of object types, O
T
. If
o
t
1
o
t
2
we say that the object type o
t
1
is a subtype
of the object type o
t
2
. Thereby the inheritance hi-
erarchy of ADOxx classes can be expressed. Due
to the generic definition, this ordering can also
be used for relationclasses: as ADOxx requires
a from-class and a to-class attribute for relation-
classes, a generic object type with these attributes
can be defined and used for the definition of sub-
types that inherit these attributes.
• the domain function maps attributes to the power
set of all object types, i.e.
domain : A →P (
[
j
O
T
j
) (5)
The domain function will constrain what objects
an attribute can map in the model instances. It is
therefore used to attach attributes to a particular
set of object types. In regard to ADOxx this cor-
responds to the assignment of ADOxx attributes
to classes and relationclasses and the definition of
an endpoint of an ADOxx relationclass.
• The range function maps an attribute to the power
set of all pairs of object types and model types, all
data types, and all model types
range :A → (6)
P
[
j
(O
T
j
×
MT
j
) ∪ D
T
∪ MT
!
In the model instances, the range function will
constrain what values an attribute can take. For
the definition of a meta model it is thus used to
specify the type of an attribute. I.e. whether the
attribute has the function of specifying the rela-
tion of an instance of an object type in a model in-
stance to either: a. the instances of object types in
a particular model type, b. instances of data types
or c. instances of model types. Case a. thus corre-
sponds to both the relationclass and interref con-
cepts in ADOxx that have an instance of a class
as a target, case b. to the ADOxx attribute con-
cepts except interref attributes, and case c. to the
ADOxx interref attribute concept that has an in-
stance of a model type as a target.
• The card function maps pairs of object types and
attributes to pairs of integers
card : O
T
× A → P (N × (N ∪ {∞})) (7)
where N is the set of non-negative integers. In the
model instances the card function will constrain
how many attribute values a object can have. In
regard to the different types of attributes this thus
permits to specify how many instances of object
types, of data types or of model types an attribute
can contain. When comparing this to the ADOxx
approach, the card function determines whether
the value of an attribute corresponds to either: a.
a target of a relationclass - that can only be one
distinct class, b. the target of an interref attribute
that can have multiple values or c. the instance of a
datatype that can also have multiple values, which
corresponds to the enumeration attribute type in
ADOxx.
In addition we define the following correctness
criteria for meta models: The sets of object types, data
types, and attributes have to be pairwise disjoint
O
T
∩ D
T
=
/
0, O
T
∩ A =
/
0, D
T
∩ A =
/
0 (8)
This follows from the fact that in mathematical terms
we have so far only been defining various sets that
could overlap. In addition, for any attribute a that is
part of the attribute set A
i
of the i-th model type - see
equation 3, the domain function for that attribute must
point to any of the object types in that model type
a ∈ A
i
⇒domain(a) ⊆ O
T
i
(9)
That ensures that attributes that are related by the
domain function to a certain object type are part of
the same model type definition. This corresponds di-
rectly to the ADOxx approach in the way that all con-
cepts that are relevant for the definition of models are
grouped within the context of a model type.
3.2 Instantiation of Meta Models
We will now describe the instantiation of a meta
model. The instantiation of a meta model essen-
tially describes the mapping of the model types, ob-
ject types, and data types to model instances, objects,
and data values together with a set of triples. Thus, an
instantiation of a metamodel MM will be a tuple
µ
mt
, µ
O
, µ
D
, T , β
(10)
where
• µ
mt
is a one-to one mapping from model types to
the power set of model instances:
µ
mt
: MT → P (mt) (11)
FDMM:AFormalismforDescribingADOxxMetaModelsandModels
137

Thereby it is defined that a model instance must
be of one specific model type and that there may
be several instances of one model type.
• µ
O
is a function taking the object types in a given
model type to collections of objects:
µ
O
:
[
j
O
T
j
× {MT
j
}
→ P (O) (12)
where
O =
[
j
µ
O
(O
T
j
× {MT
j
}
(13)
Thereby, the objects are defined as instances of an
object type O
T
j
that is part of a particular model
type MT
j
- see also equation 3. The addition of
the model type is necessary as object types may be
part of multiple model types and in the ADOxx
approach objects can only occur within a model
instance.
Sometimes it is convenient to create an object type
which is meant to be subtyped but which is not
meant to be directly instantiated. The purpose of
such a type is to capture information that is com-
mon to all the subtypes. Such a type is called an
abstract type and we can define what it means to
be an abstract type based on the definitions above.
An object type
o
t
∈ O
T
is said to be abstract if for all model types MT
i
which contain the object type o
t
(o
t
∈ O
T
i
) we have
µ
O
(o
t
, MT
i
) =
[
o
t
1
6=o
t
,o
t
1
o
t
µ
O
(o
t
1
, MT
i
).
That is to say that all the objects that instantiate
o
t
must instantiate o
t
through one of its subtypes.
In terms of ADOxx the notion of abstract types
corresponds to super classes of which one or more
of their sub classes are included in a model type
but who cannot be instantiated themselves.
• µ
D
maps data types to a power set of data objects
µ
D
: D
T
→ P (D) (14)
The data types are not further constrained. It is
thus left to the user of the formalism to ensure the
correct content of a type, e.g. whether an ’integer’
type contains only integer numbers. The formal-
ism will only ensure that a data object is assigned
a type that is valid in a particular context.
• T ⊆ O × A × (D ∪ O ∪ mt) is a set of triples.
These triples will later be used to describe the con-
tents of model instances.
• β : mt → P (T ). This map describes how the
triples are assigned to the model instances.
We will additionally define a collection of cor-
rectness constraints on the instantiation of the meta
model. These constraints fall into two categories:
disjointness constraints that describe how a model
instance is partitioned and domain/range/cardinality
constraints that constrain how attributes can map ob-
jects to other objects and data values.
The following constraints define the disjointness
and partitioning constraints that must be enforced for
the various parts of the meta model instantiation:
• The instances of object types and the instances of
datatypes must be disjoint, i.e. instances of ob-
ject types and instances of datatypes cannot be the
same.
µ
O
(o
t
, MT
j
) ∩ µ
D
(d
t
) =
/
0 (15)
• The instances of two object types are disjoint if
either the object types are disjoint or if their model
types to which they belong are disjoint, i.e. the
formalism does not permit the instantiation from
multiple object types nor a ’reuse’ of objects of the
same object type for different model instances:
i 6= j ∨ o
t
1
6= o
t
2
⇒
µ
O
(o
t
1
, MT
i
) ∩ µ
O
(o
t
2
, MT
j
) =
/
0 (16)
• For two different model types MT
i
and MT
j
also
the corresponding model instances must be dis-
joint, i.e. also for model instances no instantia-
tions from multiple model types are allowed:
MT
i
6= MT
j
⇒
µ
mt
(MT
i
) ∩ µ
mt
(MT
j
) =
/
0 (17)
• Every element of the set of model instances mt
has to be derived from a model type, i.e. there can-
not be model instances without a corresponding
model type:
mt =
[
µ
mt
(MT
j
) (18)
• For two different data types it must follow that
also their instances are disjoint, i.e. also for data
types it is not allowed that instances can be de-
rived from multiple types:
d
t
1
6= d
t
2
⇒ µ
D
(d
t
1
) ∩ µ
D
(d
t
2
) =
/
0 (19)
• T is the disjoint union of β(mt
i
) where mt
i
∈ mt.
More colloquially every triple is contained in ex-
actly one model instance.
The following constraints define the inheritance,
domain, range and cardinality constraints that the
meta model instantiation must satisfy:
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
138

• if the object type o
t
1
∈ O
T
j
is a subtype of the ob-
ject type o
t
2
∈ O
T
j
(o
t
1
o
t
2
) then we have
µ
O
(o
t
1
, MT
j
) ⊆ µ
O
(o
t
2
, MT
j
). (20)
• Sibling object types are disjoint. More specifi-
cally if o
t
1
, o
t
2
, o
t
3
∈ O
T
j
are object types such that
o
t
2
o
t
1
, o
t
3
o
t
1
,
o
t
2
6 o
t
3
, o
t
3
6 o
t
2
then
µ
O
(o
t
2
, MT
j
) ∩ µ
O
(o
t
3
, MT
j
) =
/
0. (21)
• If the value y of a statement is an object, i.e. there
is a mapping from an object type to an object for
a concrete model type MT
j
, then the pair of an
object type and a model type have to be part of
the range definition in the meta model:
(o
t
, MT
j
) ∈ range(a) (22)
(x a y) ∈ T ∧ y ∈ O ⇒
∃o
t
, MT
j
, y ∈ µ
O
(o
t
, MT
j
) (23)
The second equation further defines that if y
points to an object, then there must exist an ob-
ject type o
t
and a model type MT
j
that are part of
an µ
O
mapping for y.
• If the value y of a statement is a data object then
there must exist a datatype that is part of the range
definition of the attribute in the meta model and
there must be a mapping between the data type
and the data object:
(x a y) ∈ T ∧ y ∈ D ⇒
∃d
t
∈ D
T
d
t
∈ range(a) ∧ y ∈ µ
D
(d
t
) (24)
• If the value y of a statement is a model instance
mt, then a model type MT
j
must be part of the
range definition and the y value must correspond
to the mapping of that model type to the model
instance:
(x a y) ∈ T ∧ y ∈ mt ⇒
∃MT
j
∈ range(a), y ∈ µ
mt
(MT
j
) (25)
• For each statement the attribute a of that statement
must be part of the same model type from which
the object x has been mapped:
(x a y) ∈ T ⇒
∃ j a ∈ A
j
∧ ∃o
t
∈ domain(a), x ∈ µ
O
(o
t
, MT
j
)
(26)
• If the value y of a statement is a data object then
the data type must be part of the same model type
as the attribute:
(x a y) ∈ T , a ∈ A
i
, y ∈ D ⇒
∃d
t
∈ D
T
i
, y ∈ µ
D
(d
t
) (27)
• And for the cardinality constraints:
if x ∈ µ
O
(o
t
, MT
j
), a ∈ A
i
where
h
m, n
i
= card(o
t
, a) then m ≤
|{
y : (x a y) ∈ T ∧ y ∈ (O ∪ D ∪ mt)
}|
≤ n.
4 APPLICATION OF FDMM TO
THE 4R MODELING
LANGUAGE
To illustrate the usage of the FDMM formalism we
will show in the following how the modeling language
from the running example in section 2.3 and instances
of this modeling language can be formally described.
We start by defining the model types that will repre-
sent the 4R portfolio models and 4R business process
models by MT
PO
and MT
BP
:
MT
PO
=
O
T
PO
, D
T
PO
, A
PO
(28)
MT
BP
=
O
T
BP
, D
T
BP
, A
BP
(29)
Next, we detail the sets of object types O
T
SUP
,
O
T
PO
and O
T
BP
for expressing what corresponds to the
classes and relationclasses in ADOxx by:
O
T
PO
=
{
Business-transaction,
relates-business-transaction
}
O
T
BP
=
{
FlowOb ject, Start, Decision, Activity,
Parallelity, Join, End, 4R-event,
4R-risk-aggregation, subsequent, aggregation,
in f luences
}
(30)
Thereby, the object type FlowOb ject is defined as an
abstract type that has to be instantiated through one
of its sub types. In addition the following subtype
relationships hold between the following object types:
Start FlowOb ject
Decision FlowOb ject
Activity FlowOb ject
Parallelity FlowOb ject
Join FlowOb ject
End FlowOb ject (31)
The same is applied for detailing the sets of data
types D
T
PO
and D
T
BP
. Thereby, the Enum
view
and
Enum
in f luence
types are used to represent the ADOxx
enumeration attribute types with pre-defined values:
FDMM:AFormalismforDescribingADOxxMetaModelsandModels
139

D
T
PO
=
{
String, Float, Enum
view
}
Enum
view
=
{
Aggregated, Single
}
D
T
BP
=
String, Float, Enum
in f luence
Enum
in f luence
=
{
Time-in f luence, Cost-in f luence,
Return-in f luence,
Quality-in f luence
}
(32)
We continue by detailing the sets of attributes A
PO
and A
BP
. :
A
PO
=
{
ID, W, RE, RI, W E, ρ, relates- f rom,
relates-to, Process, View
}
A
BP
=
{
Name, ε, I, Time, Cost, Return, Quality,
In f luence-type, subsequent- f rom,
subsequent-to, aggregation- f rom,
aggregation-to, in f luences- f rom,
in f luences-to
}
(33)
For attaching the attributes to the object types and
defining their value range, we add according domain
and range definitions. This can be done for example
by attaching the Name attribute to the required object
type and then defining its range to be of the data type
String. By using the FlowOb ject abstract type we
can do this for all object types that are defined as its
subtypes:
domain(Name) =
{
FlowOb ject, 4R-risk-aggregation,
4R-event
}
range(Name) =
{
String
}
(34)
We then add the cardinality definitions for each of the
object types and their attributes as shown here exem-
plarily for the name attribute:
card(FlowOb ject, Name) =
h
1, 1
i
,
card(4R-risk-aggregation, Name) =
h
1, 1
i
,
card(4R-event, Name) =
h
1, 1
i
(35)
As it has been done for the attributes of the data type
String we can similarly define the domain, range, and
cardinality functions for an attribute of the type Float.
As already mentioned above, the FDMM formalism
does not further specify the data types so that we
would have for example:
domain(W ) =
{
Business-transaction
}
range(W ) =
{
Float
}
card(Business-transaction, W ) =
h
0, 1
i
(36)
In the same way, ADOxx attributes with pre-defined
values can be represented in FDMM as shown in the
following by inserting the data type set Enum
view
in
the range definition to specify the type of view that is
used for a business transaction:
domain(View) =
{
Business-transaction
}
range(View) =
{
Enum
view
}
card(Business-transaction, View) =
h
1, 1
i
(37)
To permit references from one object to another
model instance, e.g. to reference business transactions
to corresponding 4R business process models, the fol-
lowing domain and range definitions are needed:
domain(Process) =
{
Business-transaction
}
range(Process) =
{
MT
BP
}
card(Business-transaction, Process) =
h
0, 1
i
(38)
Finally, we also give an example for defininig the
equivalent of a relationclass based on an object type
that connects to two other object types via ”to” and
”from” attributes:
domain(in f luences- f rom) =
{
in f luences
}
range(in f luences- f rom) =
{
4R-risk-aggregation
}
card(in f luences, in f luences- f rom) =
h
1, 1
i
domain(in f luences-to) =
{
in f luences
}
range(in f luences-to) =
{
Activity
}
card(in f luences, in f luences-to) =
h
1, 1
i
(39)
Also for such an object type, that corresponds to a
relationclass, attributes can be added in the same way
as shown above:
domain(In f luence-type) =
{
in f luences
}
range(In f luence-type) =
Enum
in f luence
card(in f luences, In f luence-type) =
h
1, 1
i
(40)
When defining relationclasses that can be used to con-
nect multiple classes, the definition can be simplified
by reverting to a supertype class as for example the
FlowOb ject class and the subsequent relationclass:
domain(subsequent- f rom) =
{
subsequent
}
range(subsequent- f rom) =
{
FlowOb ject
}
card(subsequent, subsequent- f rom) =
h
1, 1
i
domain(subsequent-to) =
{
subsequent
}
range(subsequent-to) =
{
FlowOb ject
}
card(subsequent, subsequent-to) =
h
1, 1
i
(41)
Based on these definitions for the model type we
can describe the instantiation of a concrete model. As
an example we use two models that have been de-
scribed in (Fill et al., 2007) - see figures 3 and 4. They
represent sample instances of a 4R portfolio model
type and a 4R business process model type that shows
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
140
how 4R events and 4R risk aggregations are used to
represent the influence of risks on the accomplish-
ment of activities. We will use these models to de-
scribe some of its contents by using the FDMM for-
malism.
W: 25,00
RE:
55,00
RI:
60,00
WE: 23,00
RE: 35,00
RI: 24,00
2_Sample_Process
ρ:0,400
WE: -2,50
RE: 10,00
RI: 25,00
4_Sample_Process
W: 25,00
RE:
45,00
RI:
40,00
ρ:1,00
P Q
2
4
ρ:0,500
ρ:0,600
Figure 3: Excerpt of a 4R Portfolio Model (Fill et al., 2007).
Process
Start
Decision
Activity A
Sick
employee
Activity B
Acquired
staff costs
ʌ
Acquired
waiting time
ʌ
Increase of
taxes
Delayed
supplies
Machine
failure
ε=0,200
I=5,000
ε=0,020
I=3,000
ε=0,020
I=10,0
ε=0,050
I=8,0
Figure 4: Excerpt of a 4R Business Process Model - trans-
lated from (Fill et al., 2007).
First we instantiate concrete models for the model
types MT
PO
and MT
BP
based on a mapping from the
meta model definition:
µ
MT
(MT
PO
) =
{
mt
po1
}
µ
MT
(MT
BP
) =
mt
bp1
(42)
Next, we instantiate objects based on mappings from
the object types. We show this exemplarily for some
instances of the business transaction, activity, 4R
event, and 4R aggregation object types:
µ
O
(Business-transaction, MT
PO
) =
{
BT
P
, BT
Q
}
µ
O
(Activity, MT
BP
) =
{
Activity
A
,
Activity
B
}
µ
O
(4R-event, MT
BP
) =
{
Machine- f ailure,
Delayed-supplies
}
µ
O
(4R-aggregation, MT
BP
) =
{
Acquired
-waiting-time
}
(43)
Similarly we can instantiate object types that can
later act as relations such as the influences type:
µ
O
(in f luences, MT
BP
) =
{
in f luences
1
, in f luences
2
}
(44)
Subsequently, we also show the mappings of some
data types to data objects in order to later assign them
as values for attributes:
µ
D
(String) =
0
ActivityA
0
,
0
ActivityB
0
,
0
DelayedSupplies
0
,
0
Machine f ailure
0
,
Acquired-waiting-time
}
µ
D
(Float) =
{
25.00, 55.00, 60.00
}
µ
D
(Time-in f luence) =
0
time-in f luence
0
(45)
And finally we can define the relationships between
the objects and the data object by using the attributes
in the form of triple statements, e.g. to express the
names of concrete objects and the values of attributes
and defining relations:
(Activity
A
Name
0
ActivityA
0
) ∈ β(mt
bp1
),
(BT
P
W 25.00) ∈ β(mt
po1
),
(in f luences
1
in f luences- f rom
Acquired-waiting-time) ∈ β(mt
bp1
),
(in f luences
1
in f luences-to Activity
B
) ∈ β(mt
bp1
)
(46)
And for detailing the type of influence by specifying
the attribute value that is available based on a pre-
defined data type:
(in f luences
1
In f luence-type
0
time-in f luence
0
)
∈ β(mt
bp1
)
(47)
5 DISCUSSION
With the description of the FDMM formalism it be-
came possible for the first time to formally describe
FDMM:AFormalismforDescribingADOxxMetaModelsandModels
141

the core constituents of ADOxx based modeling lan-
guages. Thereby, the particular ways for defining
meta models in ADOxx can now be analyzed and
made available for comparisons with other meta mod-
eling approaches. This concerns in particular the
way how model types and relations between differ-
ent model and class instances are represented. As
a result, also mappings and transformations to other
meta modeling approaches can now be facilitated us-
ing FDMM. In addition, FDMM can be of benefit
especially for the further development of the Open
Models Initiative and the numerous ADOxx modeling
languages that are being developed by its projects.
As FDMM is able to formally describe the core
ADOxx constituents but does not formalize the
ADOxx approach as such, it has to be distinguished
between the concepts as they are used within the
ADOxx platform and the concepts as they are speci-
fied in the FDMM formalism. Due to the limitation of
space we will here only discuss the main distinguish-
ing features based on the set of eight categories of
meta modeling concepts by (Kern et al., 2011). These
categories are: characteristics of first class concepts,
relationships, attributes, inheritance, links to models,
groupings, and the type of constraint language used.
In table 1 the values for the characteristics are shown.
It thus becomes obvious that concerning the first
class concepts and the use of inheritance, FDMM is
more generic than ADOxx. As the relationships are
not described by first class objects in FDMM but by
combinations of object types and attributes together
will cardinalities – as shown e.g. in equation 39 –
their arity is also set to n-ary. In ADOxx this is re-
alized using interref attributes to connect to multiple
objects. ADOxx further provides the constraint lan-
guage ADOscript for checking and analyzing com-
plex semantic constraints in models, which is cur-
rently not available in FDMM. Based on these char-
acteristics ADOxx and FDMM can now also be com-
pared to other meta modeling approaches. This will
be discussed in section 6.
The application of FDMM to the 4R modeling lan-
guage showed how the formalism can be used for
a concrete example. Due to small number of con-
structs that are required for describing meta models
and models in FDMM this could be easily accom-
plished. At the same time all parts of the modeling
language could be successfully represented. Further-
more, in the context of the 4R modeling language the
availability of a formal description is particularly ben-
eficial for the definition of algorithms. It can now be
easily determined which data types and structures are
required for designing algorithms that perform calcu-
lations on the risk and return figures laid down in the
4R modeling language, and how they relate to the ele-
ments in the models. Based on the FDMM formalism
such algorithms can now also be described indepen-
dently of a concrete implementation.
6 RELATED WORK
When comparing FDMM and ADOxx to similar ap-
proaches in the literature, two directions can be taken.
The first is the comparison to other meta model-
ing approaches and the second is the comparison to
other kinds of formalizations for meta modeling ap-
proaches.
Based on the classification proposed by (Sprinkle
et al., 2010), the FDMM and the ADOxx meta mod-
eling approach directly compare to domain-specific
modeling approaches that view meta models as lan-
guage specifications. This is in contrast to approaches
that treat meta models as software structure specifi-
cations, which is the typical use case for approaches
such as EMOF (Object Management Group, 2011),
EMF (McNeill, 2008) or KM3 (Jouault and Bezivin,
2006). A common aspect of domain-specific mod-
eling approaches is the creation of visual model ed-
itors from meta models that are based on one pre-
defined meta meta model and that use a graphical rep-
resentation for the concrete syntax of the defined lan-
guage. (Kern et al., 2011) also denote this direction
as heavyweight approaches of language definition and
distinguish it from lightweight approaches that adapt
a generic meta model with domain-specific concepts.
An example for the latter direction would be the use
of the profile package in UML, e.g. to extend existing
meta classes with the stereotyping mechanism (OMG,
2004).
In regard to the meta modeling concepts as shown
in table 1, FDMM and ADOxx can be directly com-
pared to the approaches analyzed in (Kern et al.,
2011): thereby a core feature of ADOxx and FDMM
that is shared with the GME and ARIS meta modeling
approaches is the use of model types for defining the
grouping of object types and their instances. In con-
trast to all approaches compared by Kern et al. and
ADOxx, FDMM does not use any relation concept
as a first class concept. Neither ADOxx nor FDMM
use explicit role type concepts that provide further
mechanisms for specifying relationships such as se-
mantic dependencies between object types. However,
in ADOxx such concepts can be expressed using the
ADOscript language and enforced during modeling.
For the meta modeling approaches mentioned
above, formalizations have been discussed for
EMOF e.g. (Poernomo, 2006; Favre, 2010) and
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
142

Table 1: Comparison of Meta Modeling Concepts of ADOxx and FDMM.
ADOxx FDMM
First Class Concepts Model Type, Class, Relationclass Model Type, Object Type, Data Type, Attribute
Arity of Relationships n-ary (using interref) n-ary
Attributes single-value/multi-value single-value/multi-value
Inheritance single (Class only) single (Object Types only)
Links to Models yes yes
Grouping Model Types Model Types
Constraint Language ADOscript none
KM3 (Jouault and Bezivin, 2006). However, they dif-
fer from ADOxx in regard to their focus on the spec-
ification of software structures. Another approach
that shows some similarities to the way the FDMM
formalism has been conceived can also be found in
the specification of the Object Constraint Language
(OCL) (OMG, 2010)[Annex A]. However, the main
difference is that FDMM is directed towards support-
ing the representation of meta models and models.
The OCL specification does not describe a meta mod-
eling approach but rather an approach to formalize
one particular modeling language, i.e. UML together
with constraints.
Furthermore, the domain, range, and card func-
tions and the associated constraints described for
them have a similarity with the notions of domain,
range and cardinality restrictions used in in descrip-
tion logics (Baader, 2003). In contrast to the descrip-
tion logic case, our work is not intended to give a se-
mantics for some formal language. Instead it is in-
tended to provide a formal description of an existing
system that has been effectively used in several appli-
cation domains.
7 CONCLUSIONS AND
OUTLOOK
In this paper we presented a formalism to describe the
core constituents of the ADOxx meta modeling ap-
proach and showed its application to a concrete mod-
eling language. It is the first formal definition for
ADOxx meta modeling concepts and is therefore ex-
pected to be of benefit also for other projects using the
ADOxx approach. Future work will therefore include
the application to further modeling languages and the
evaluation of the usability of the formalism. This con-
cerns in particular the definition of algorithms, e.g. for
describing analyses and simulations of models. Fi-
nally, it will also be investigated how the formalism
can be represented visually to enhance the interac-
tion with it and enable the easy re-use of formal meta
model and model statements.
ACKNOWLEDGEMENTS
Parts of the work on this paper have been funded by
the Austrian Science Fund (FWF) in the course of an
Erwin-Schr
¨
odinger fellowship project number J3028-
N23.
REFERENCES
Baader, F. (2003). The description logic handbook: theory,
implementation, and applications. Cambridge Univ
Pr.
Borgida, A., Chaudhri, V., Giorgini, P., and Yu, E. (2009).
Conceptual Modeling: Foundations and Applications.
Springer.
Bork, D. and Sinz, E. (2010). Design of a SOM Business
Process Modelling Tool based on the ADOxx meta-
modelling Platform. In De Lara, J. and Varro, D., ed-
itors, Proceedings of the Fourth International Work-
shop on Graph-Based Tools. EASST.
Braun, C. and Winter, R. (2005). A comprehensive en-
terprise architecture metamodel and its implementa-
tion using a metamodeling platform. In Desel, J. and
Frank, U., editors, Enterprise Modelling and Informa-
tion Systems Architectures, pages 64–79. Gesellschaft
fuer Informatik, Bonn.
Demirkan, H., Kauffman, R. J., Vayghan, J. A., Fill, H.-
G., Karagiannis, D., and Maglio, P. (2008). Service-
oriented technology and management: Perspectives
on research and practice for the coming decade.
Electronic Commerce Research and Applications,
7(4):356–376.
Faisst, U. and Buhl, H. (2005). Integrated Enter-
prise Balancing mit integrierten Ertrags- und Risiko-
datenbanken (German: Integrated Enterprise Bal-
ancing with integrated Return and Risk Databases).
Wirtschaftsinformatik, 47(6):403–412.
Favre, L. M. (2010). Formalization of MOF-Based Meta-
models. In Favre, L. M., editor, Model Driven Archi-
FDMM:AFormalismforDescribingADOxxMetaModelsandModels
143

tecture for Reverse Engineering Technologies. Infor-
mation Resources Management Association.
Fill, H.-G. (2009). Visualisation for Semantic Information
Systems. Gabler.
Fill, H.-G., Gericke, A., Karagiannis, D., and Winter, R.
(2007). Modellierung fuer Integrated Enterprise Bal-
ancing (German: Modeling for Integrated Enterprise
Balancing). Wirtschaftsinformatik, 06/2007:419–429.
Gericke, A., Fill, H.-G., Karagiannis, D., and Winter, R.
(2009). Situational Method Engineering for Gover-
nance, Risk and Compliance Information Systems. In
DESRIST. ACM.
Harel, D. and Rumpe, B. (2000). Modeling languages: Syn-
tax, semantics and all that stuff - part i: The basic stuff.
Technical Report MCS00-16, The Weizmann Institute
of Science.
Harel, D. and Rumpe, B. (2004). Meaningful modeling:
What’s the semantics of ”semantics”? IEEE Com-
puter, October 2004:64–72.
Harmon, P. (2010). The BPTrends 2010 BPM Soft-
ware Tools Report on BOC’s Adonis Version 4.0.
http://www.bptrends.com/publicationfiles/2010%
20BPM%20Tools%20Report-BOCph.pdf last ac-
cessed 10-10-2011.
Hinkelmann, K., Nikles, S., Wache, H., and Wolff, D.
(2010). An enterprise architecture framework to or-
ganize model repositories. In Woitsch, R. and Micsik,
A., editors, OKM Open Knowledge Models, Workshop
W3 at EKAW 2010.
Hofer, S. (2011). Instances over algorithms: A different ap-
proach to business process modeling. In Johannesson,
P., Krogstie, J., and Opdahl, A., editors, The Prac-
tice of Enterprise Modeling. 4th IFIP WG 8.1 Working
Conference, Oslo. Springer.
Jouault, F. and Bezivin, J. (2006). KM3: a DSL for Meta-
model Specification. In Proceedings of 8th IFIP In-
ternational Conference on Formal Methods for Open
Object-Based Distributed Systems, pages 171–185.
Springer.
Junginger, S., Kuehn, H., Strobl, R., and Karagian-
nis, D. (2000). Ein Geschaeftsprozessmanagement-
Werkzeug der naechsten Generation - ADONIS:
Konzeption und Anwendungen (German: ADONIS:
A next generation business process management tool
- Concepts and Applications). Wirtschaftsinformatik,
42(5):392–401.
Karagiannis, D., Fill, H.-G., Hoefferer, P., and Nemetz, M.
(2008a). Metamodeling: Some application areas in in-
formation systems. In Kaschek, R. and et al., editors,
UNISCON, pages 175–188. Springer.
Karagiannis, D., Grossmann, W., and Hoefferer, P.
(2008b). Open model initiative - a feasibility study.
http://cms.dke.univie.ac.at/uploads/media/Open
Models Feasibility Study SEPT 2008.pdf.
Karagiannis, D., Junginger, S., and Strobl, R. (1996). In-
troduction to Business Process Management Systems
Concepts. In Scholz-Reiter, B. and Stickel, E., editors,
Business Process Modelling, pages 81–106. Springer,
Berlin et al.
Karagiannis, D. and Kuehn, H. (2002). Metamod-
eling platforms. In Bauknecht, K., Min Tjoa,
A., and Quirchmayr, G., editors, EC-Web 2002
at Dexa 2002, page 182. Springer, Aix-en-
Provence, France. Full version available at:
http://www.dke.univie.ac.at/mmp/FullVersion MMP
DexaECWeb2002.pdf.
Kaschek, R. (2008). On the evolution of conceptual model-
ing. In Dagstuhl Seminar Proceedings, volume 08181.
Kern, H., Hummel, A., and Kuehne, S. (2011).
Towards a comparative analysis of meta-
metamodels. In The 11th Workshop on
Domain-Specific Modeling, Portland, USA.
http://www.dsmforum.org/events/DSM11/Papers/
kern.pdf (last access 05-01-2012).
Koch, S., Strecker, S., and Frank, U. (2006). Conceptual
Modelling as a New Entry in the Bazaar: The Open
Model Approach. In Open Source Systems, volume
203/2006, pages 9–20. IFIP International Federation
for Information Processing.
Kuehn, H. (2010). The ADOxx Metamodelling
Platform. In Workshop on Methods as Plug-
Ins for Meta-Modelling, Klagenfurt, Austria.
http://www.openmodel.at/c/document library/get
file?uuid=7516b7c5-a525-4d92-929e-
6c11e5da9d39&groupId=10122.
McNeill, K. (2008). Metamodeling with EMF:
Generating concrete, reusable Java snippets.
http://www.ibm.com/developerworks/library/os-
eclipse-emfmetamodel/index.html?S TACT=105AG
X44&S CMP=EDU.
Nemetz, M. (2006). A meta-model for intellectual capi-
tal reports. In Karagiannis, D. and Reimer, U., ed-
itors, Proceedings of the 6th International Confer-
ence on Practical Aspects of Knowledge Management.
Springer.
Object Management Group (2011). Omg meta ob-
ject facility (mof) core specification version 2.4.1.
http://www.omg.org/spec/MOF/2.4.1/PDF/.
OMG, O. M. G. (2004). Unified modeling language (uml)
specification: Infrastructure version 2.0. Technical re-
port. http://www.omg.org/docs/ptc/04-10-14.pdf ac-
cessed 12-03-2006.
OMG, O. M. G. (2010). Object constraint lan-
guage specification version 2.2. Technical report.
http://www.omg.org/spec/OCL/2.2 accessed 11-01-
2012.
Poernomo, I. (2006). The Meta-Object Facility Typed. In
SAC’06, pages 1845–1849, Dijon, France. ACM.
Schwab, M., Karagiannis, D., and Bergmayr, A. (2010).
i* on ADOxx(R): A Case Study. In Proceedings of
the 4th International i* Workshop - iStar10 - CAiSE
Workshop Proceedings, pages 92–97. Springer.
Sprinkle, J., Rumpe, B., Vangheluwe, H., and Karsai, G.
(2010). Metamodelling - state of the art and research
challenges. In Giese, H. et al. , editor, MBEERTS,
volume LNCS 6100, pages 57–76. Springer.
Wand, Y. and Weber, R. (2002). Research commen-
tary: Information systems and conceptual modeling
- a research agenda. Information Systems Research,
13(4):363–376.
ICEIS2012-14thInternationalConferenceonEnterpriseInformationSystems
144
