The Improved SSR Electromagnetic Simulation Model

and Its Comparison with Field Measurements

Xiaorong Xie

, Yipeng Dong

, Kai Bai

, Xun Gao

and Ping Liu

State Key Lab. of Power System, Department of Electrical Engineering, Tsinghua University, Beijing 100084, China

North China Electric Power Research Institute Co., Ltd, Xicheng District, Beijing 100045, China

North China Grid Co., Ltd, Power Dispatch Center, Xicheng District, Beijing 100053, China

Keywords: Subsynchronous Resonance, Electromagnetic Simulation, Series Compensation.

Abstract: Electromagnetic simulation (EMS) plays an important role in the evaluation of subsynchronous resonance

(SSR). To meet the requirement of practical engineering, this paper discusses how to improve the modeling

method of SSR-EMS in three important aspects, i.e., the shaft system of turbine generator, the series

compensation and the supplementary excitation damping controller (SEDC). Thus a systematically

improved EMS model was put forward, which includes a lumped mass-spring model with adjustable and

non-linear mechanical damping, a series compensation model incorporating MOV with the gap protection

logic and an engineering model of SEDC to reflect the dynamics of the power-electronic exciter. The

developed model overcomes the shortage of the traditional one and is applicable to the accurate analysis on

SSR stability, transient torque and fatigue expenditure when the system experiences large disturbances. The

proposed method is then used for the simulation of a real SSR event caused by a short-circuit fault in the

Shangdu series-compensated power system. The simulation results are compared with the field

measurements and a good consistence is found. Consequently, the improved EMS model is proved to be

applicable, accurate and effective for SSR analysis in practical engineering.

1 INTRODUCTION

With the wide application of series compensation in

power systems, the SSR issue attracts more and

more attentions (SSR W.G., 1992). SSR analysis

plays an important role in evaluating its risks and

selecting countermeasures. Currently, such methods

as frequency-scanning, complex torque coefficient,

eigenvalue analysis and electromagnetic simulation

(EMS) are widely applied (Yu et al., 2006; Canay,

1982; Hara et al., 1994). Among these methods, the

time-domain EMS, despite of its complicated

modeling and heavy computation, possesses obvious

advantages as follows:

1) Capable of modeling system nonlinearities;

2) Applicable to the analysis of multi-mode

torsional oscillation in multi-machine systems;

3) Able to analyze either large or small

disturbances, and to provide dynamic response and

output in the sense of electromagnetic transients;

4) Suitable for the evaluation of various

SSR-damping devices, such as the supplementary

excitation damping control (SEDC).

Therefore, EMS becomes an indispensible tool

for SSR analysis in engineering application.

Currently, this analysis method is mainly depend on

commercial software like PSCAD/EMTDC

(Kajoijilertsakul et al., 2011), which can provide the

basic models and numerical method required by

SSR analysis and meet the general analysis demand.

However, there are some problems requiring

attention and improvement. To meet the requirement

of practical engineering, this paper mainly focuses

on the modeling improvement in three aspects:

1) The mechanical damping of the T-G shaft

system, assumed in many studies to be a fixed value,

should be modeled as a function of the T-G’s

working condition (Xie and Zhang et al., 2011).

2) The nonlinearities of the metal oxide varistor

(MOV), the gap and other protective devices should

be incorporated for accurate modeling of a

real-world series compensation.

3) The power-electronic circuit of the excitation

system is regarded as an “instantly” established

circuit during electromechanical transients. However,

there is a time-delay, which will affect the dynamics

419

Xie X., Dong Y., Bai K., Gao X. and Liu P..

The Improved SSR Electromagnetic Simulation Model and Its Comparison with Field Measurements.

DOI: 10.5220/0003973704190424

In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2012),

pages 419-424

ISBN: 978-989-8565-20-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

of exciter-based SEDC control system, thus making

it necessary to refine its modeling.

This paper attaches great emphasis on the

modeling improvement in the mentioned aspects,

and applies it in a real electric network, i.e., the

Shangdu series-compensated power system. Then,

EMS results are compared with the actually

recorded data to prove its accuracy, applicability and

efficiency of the improved simulation method.

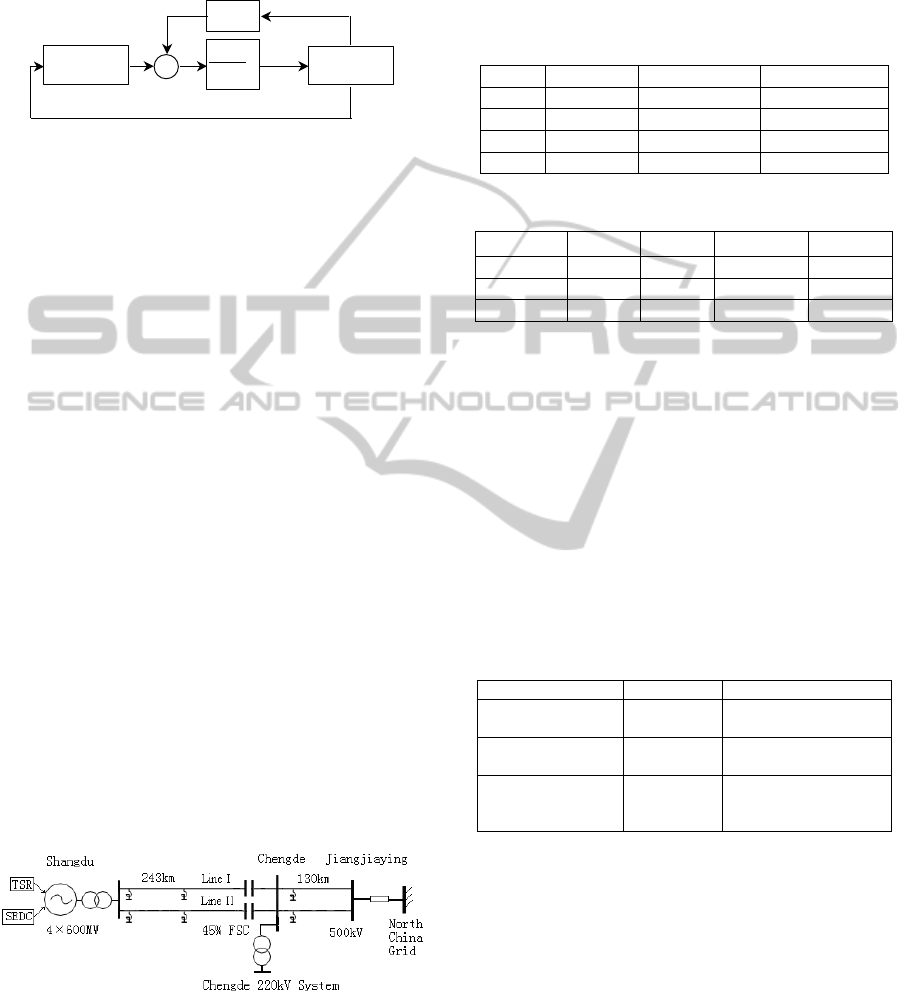
2 THE IMPROVED MASS-

SPRING SHAFT MODEL OF

THE TURBINE-GENERATOR

For SSR evaluation, a turbine-generator (T-G) is

represented as a lumped mass-spring model (IEEE

Committee report, 1977, 1985; Baker et al., 2005).

For instance, the widely used 600MW T-G in China

is expressed by a 4-mass spring model, as in Figure

1. It has 4 rotors, i.e., a high-and-

intermediate-pressure turbine (HIP), two low-

pressure turbines (LPA/LPB), and a generator rotor.

Figure 1: The lumped T-G shaft system.

Representing the T-G as inertias connected by

shafts of appropriate stiffness, the dynamic equation

for the spring-mass system may be written as (1)

   Mδ Dδ Kδ TT

(1)

Where:

is the torsional angle displacements

column matrix;

is a diagonal matrix

representing the inertias of masses;

is the

damping coefficient matrix;

is a tri-diagonal

matrix of torsional stiffness;

are vectors of

mechanical and electrical torques respectively.

Model (1) is widely adopted in EMS softwares

like PSCAD/EMTDC. However, it has several

drawbacks in practice: The damping matrix

can

neither be provided by the manufacturer nor be

measured through test directly. Actually it is a

nonlinear function of system condition and cannot

be interpreted by model (1). But in PSCAD/EMTDC,

its value can only be set fixed rather than

self-adjustable. As a result, when operating status

changes, it is impossible to achieve accurate EMS.

Model (1) is improved in view of these

shortages. Specifically, implement model

decoupling transformation to model (1). That is,

have

δ Qδ

, and have equation (1) left multiplied

, where the model decoupling matrix

the right eigenvector of

-1

. Then, model (1)

can be transformed into the canonical form as (2):

m m m m m m m

   M δ D δ K δ T

(2)

Where

δ Qδ

m m e

= ( )T Q T T

M Q MQ

K Q KQ

D Q DQ

In model (2), although the coefficient matrices

and

are decoupled into diagonal

matrices, it is still impossible for the damping

coefficient matrix

to achieve complete

decoupling since it is not a diagonal matrix.

However, as the coupling damping between modes

is usually assumed to be small and can be almost

contained within the damping of each mode, the

non-diagonal elements of

are ignored. This

means to have

 

m md 1 2 3

diag , , , 0

m m m

d d dDD

(where 0 represents the damping of

electromechanical mode), thus realizing the

decoupling among torsional modes. So each natural

mode is governed by an equation of the form:

m mm m m m m m

, 1,...,

k k k k k k k

M d K T k N

  

    

(3)

where the subscript

denotes each of the

decoupled torsional modes.

Compared with model (1), model (3) is

advantageous in achieving decoupling of torsional

mode, and replacing the complicated

with

modal damping

, which can be measurable via

various methods, e.g., the excitation-injection test

and the system-side disturbance test. Furthermore, it

is possible to set

as a nonlinear function of

generator variables and to simulate its actual

variation with the constantly changing system

conditions in EMS. According to our actual

measurements, the modal mechanical damping can

be expressed by the non-linear function:

m0 m

m m0 m

ed k P c







  

(4)

Where





is the modal speed deviation,

the power of the unit, and

m0 m0 m

, , , kc



are

coefficients, which can be determined with a method

like that proposed in literatures (Xie and Zhang et al.,

2011).

SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

420

3 THE IMPROVED MODEL OF

SERIES COMPENSATION

The fixed series compensation (FSC), as shown in

Figure 1, consists of series capacitor banks and

corresponding protection devices such as MOV,

current-limiting damping elements, protective gap

and by-pass switch. MOV and the protective gap,

though exert no impact on SSR stability during

small disturbances, have significant impact on the

transient torque, especially during the fault

occurrence and a period of time after the fault.

Therefore, it is necessary for EMS to take the

nonlinear characteristics of MOV, the protective

gap and the by-pass switch into account,

especially when there’s a need to analyze the

transient torque and the consequent fatigue

expenditure of the generator shaft following large

disturbances. Figure 3 is the improved modelling

of FSC in our EMS method, among which:

1) MOV is expressed by the series circuit

composed of controllable voltage source and

non-linear resistance. Its V-I characteristic is

described with an external file.

2) The protective gap and the by-pass switch

are replaced by an ideal switch with specific logic

of protection to simulate MOV’s various

protective actions: a delayed monostable trigger

signal is output when the current or the energy of

MOV exceeds the set value, and thus the switch

for controlling the ideal by-pass is turned on for a

set time period and then turned off again.

The FSC model in Figure 2 is able to simulate

the general actual logic of the practical series

capacitor as well as its protective circuit when

experiencing large disturbances. Since the energy

exchange between the series capacitor and the

generator determines the SSR dynamic, especially

the transient torque of the shaft, this model can

accurately reflect the actual dynamics of FSC.

Figure 2: Schematic of FSC.

Figure 3: Electromagnetic model of FSC.

4 THE ELECTROMAGNETIC

MODEL OF SEDC

SEDC is a real-time control system that works

through the excitation system by modulating the

field voltage at torsional frequencies. Figure 4

illustrates the relationship of the SEDC (Xie and

Guo et al., 2011), the excitation regulator, the

generators and the grid. As a supplementary control,

SEDC uses the mechanical speed of the HIP turbine

(



) to generate the subsynchronous control output

(

SEDC

). However, the well-established

electromechanical transient model of the

excitation system cannot be applied directly in

SSR-EMS, because the control frequency (300Hz)

of the thyristor in the power-electronic circuit, i.e.,

the three-phase fully-bridge controlled rectifier

bridge, is much higher than that of DC and

low-frequency components, on which the

electromechanical transient analysis focuses. In

other words, it is reasonable to ignore the

dynamics of the power-electronic circuit in

electromechanic analysis and regard it as an ideal

“algebraic” converter. But in SSR-EMS, the

dynamic characteristics of the power-electronic

exciter must be considered because the torsional

frequencies (generally from 10 to 40Hz) and the

control frequency of thyristor are comparable.

Based on tests on the exciters of large generators,

a refined EMS model of the excitation system with

SEDC is proposed, as shown in Figure 4, in which,

the power-electronic circuit of the exciter is

expressed by a first-order-plus-time-delay transfer

function. The dead time delay (

) represents the

computational delay of the control law and the

transport delay of the thyristor, while the first-order

function is used to approximate the dynamics of the

power-electronic circuit. Although

, generally

from several to a dozen milliseconds, are very

The Improved SSR Electromagnetic Simulation Model and Its Comparison with Field Measurements

421

small compared with electromechanical transients,

they are comparable with the period of torsional

modes and thus have significant impact on the

tuning of SEDC parameters.





GEN

AVR/PSS



, P



SEDC



Figure 4: EMS model of the SEDC and excitation system.

5 VERIFICATION OF THE

IMPROVED MODEL

The improved EMS model proposed above has been

applied in many practical SSR studies. Here a

short-circuit fault that occurred in a real system is

used to verify its effectiveness.

5.1 The Shangdu System

Shangdu Power Plant (SPP) is located in Inner

Mongolia Autonomous Region, about 300km north

of Beijing. It has four 600MW turbine-generators

connected to North China Power Grid through 500

kV lines, as shown in Figure 5. To improve transfer

capability and system stability, FSCs are applied to

the two lines between SPP and Chengde substation

with 45% compensation degree. Each turbine-

generator consists of four rotors, as shown in Figure

1, resulting in three torsional modes, of which the

frequencies (in Hz) are listed in Table 1. Previous

study indicated that the generator suffered serious

SSR if one of the two Shangdu-Chengde lines is

switched off for any reason (Xie and Guo et al.,

2011). Thus SEDC and torsional stress relay (TSR)

were developed to solve the problem. SEDCs, TSRs

and FSCs were put into practical operation in 2007.

Figure 5: The one-line diagram of the Shangdu system.

5.2 Parameters of the Improved

Models

1) The turbine-generator shaft

The torsional frequencies of the four generators

are shown in Table 1. The typical coefficients of the

mechanical damping model (3) were obtained with

field-test data and listed in Table 2. To save place,

other shaft model parameter won’t be listed here.

Table 1: Modal Frequencies of the Shangdu T-Gs.

Gen.#

mode #1

mode #2

mode #3

15.33

26.12

30.54

15.32

26.12

30.52

15.22

26.04

30.51

15.19

26.01

30.25

Table 2: Coefficients of the mechanical damping model.

Mode #





0.010

25.2

0.005

0.135

0.007

31.0

0.006

0.135

0.005

20.0

0.012

0.180

2) The excitation system with SEDC

The standard IEEE ST4B AVR and IEEE PSS2B

PSS models (Kamwa et al., 2005) are modified to

represent the excitation system with SEDC included,

of which the critical time constants are measured

through filed tests, i.e.,

8.0 ms, 4.0 ms

TT

3) MOV and the protective gap

MOV has three types of protection, as shown in

Table 3. Once MOV protection is triggered, the gap

is controlled to spark within 2 ms and then

capacitors are bypassed for a time period (generally

3 seconds) or until the fault is completely cleared.

Table 3: The settings of MOV and the protective gap.

MOV protection

Settings

Actions

Over-current

12 kApeak

Gap spark and

single-phase bypassed

Excess-energy

bypass

22 MJ

Gap spark and

single-phase bypassed

Excess-energy

bypass without

reclosing

26 MJ

Gap spark, 3-phase

bypassed with the

recloser locked

5.3 The Short-circuit Fault

On August 8, 2010, the system operated normally

before the fault. At 20:16:58, a phase-to-ground

fault happened on phase-A due to a lightning strike

on Line II at 88km from Shangdu. The faulted line

was tripped from Chengde and Shangdu sides after

55 and 63 milliseconds respectively. The recloser at

Shangdu side reclosed successfully. However, the

recloser at Chengde side failed and then phases B

and C were tripped off about 89 milliseconds after

the fault. Consequently, Line II was disconnected at

SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

422

Chengde side. Divergent SSR appeared at Units #1

and #2. TSR then tripped Unit #1 about 3.546

seconds following the fault. Thus SSR converged

rapidly. However, 6.388 seconds later, Unit #2 was

tripped by its TSR because the accumulated fatigue

loss-of-life exceeded its setting values. During the

process, the shaft speed data were recorded.

5.4 Actual Measurements Vs.

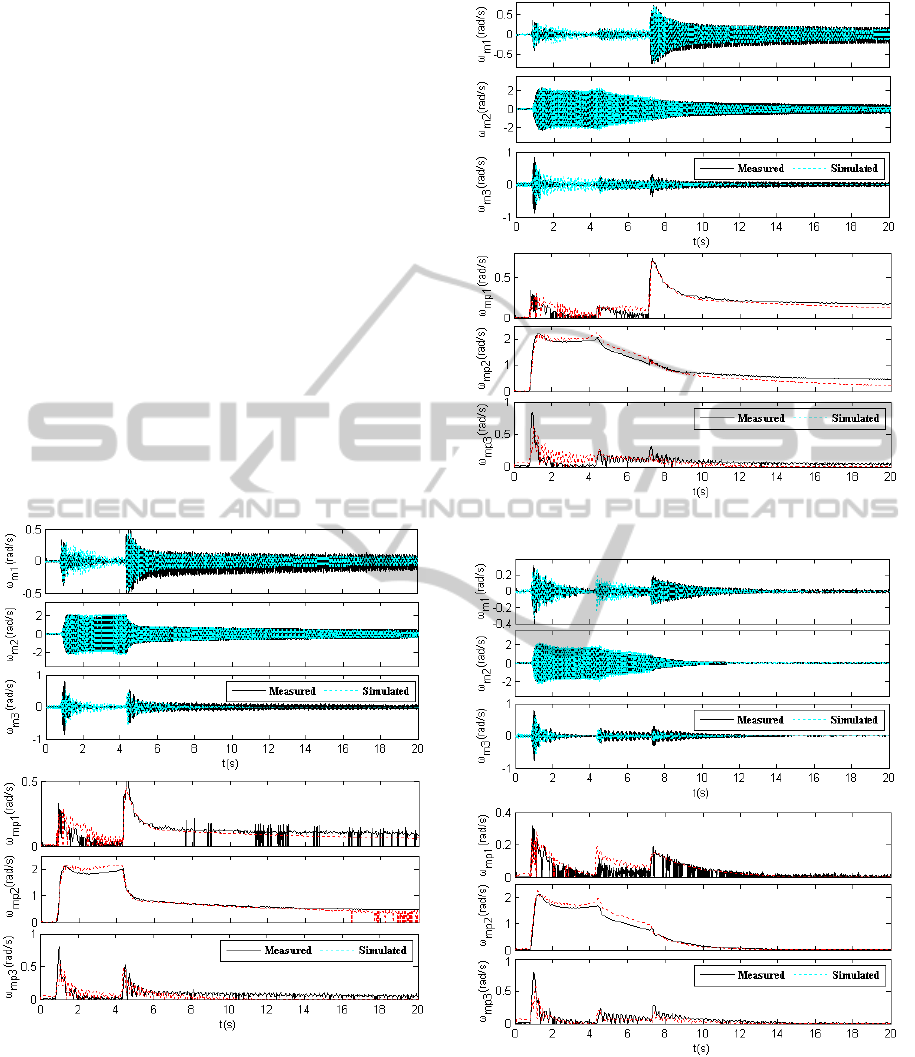
Simulations

A specific analysis on the above-mentioned fault

was carried out with the improved SSR-EMS model.

The simulation results are compared with actual

measurements, as illustrated in Figures 6-9, in which

the modal speeds of each generator as well as its

corresponding upper envelope are plotted. It can be

obviously observed that the actual measurements are

basically in accordance with the simulated curves.

Of course, there are some inconsistent “burs” on the

upper envelopes for actual measurement due to

noises in the obtained signals.

Figure 6: Measured vs. simulated SSR dynamics (unit #1).

Figure 7: Measured vs. simulated SSR dynamics (unit #2).

Figure 8: Measured vs. simulated SSR dynamics (unit #3).

The Improved SSR Electromagnetic Simulation Model and Its Comparison with Field Measurements

423

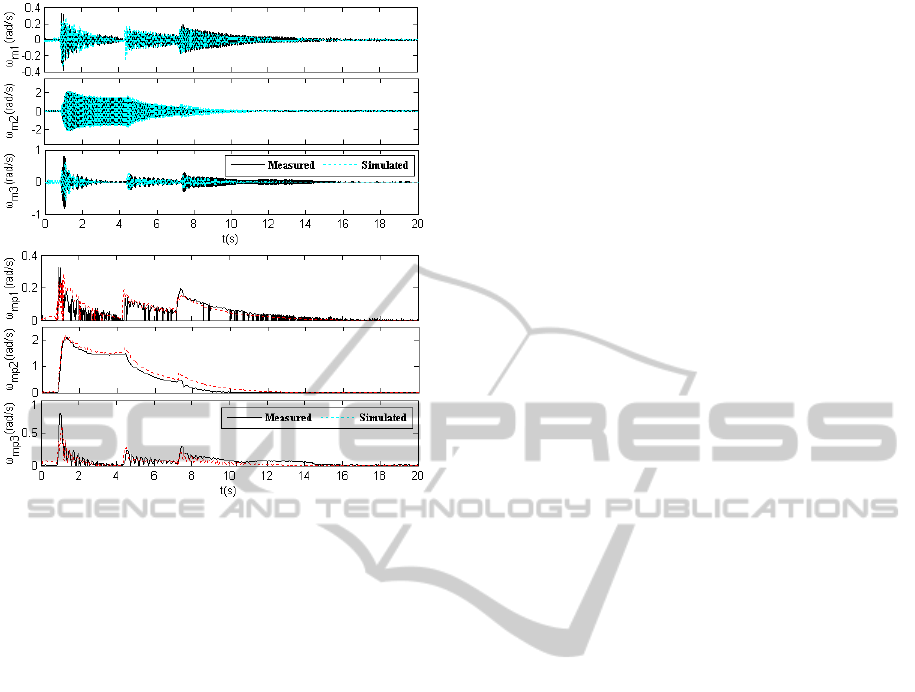
Figure 9: Measured vs. simulated SSR dynamics (unit #4).

6 CONCLUSIONS

Electromagnetic simulation is critical to SSR

analysis and control-design. This paper presents

several improvements in the modeling of SSR-EMS:

i) the lumped mass-spring model with adjustable and

nonlinear mechanical damping to simulate the

variation of mechanical damping under different

operating conditions and system disturbances; ii) a

series compensation model incorporating MOV and

the gap protection logic for accurate modeling of

practical FSC when confronted with serious faults;

iii) an EMS model of SEDC to reflect the dynamics

of the power-electronic exciter. To verify the

effectiveness, the improved model is used to analyze

a short-circuit fault that occurred in a real system,

i.e., the Shangdu series-compensated power system.

The simulation results are compared with the field

measurements and a good consistency is discovered.

ACKNOWLEDGEMENTS

This work is supported by National Natural Science

Foundation of China (51077080 and 51037002) and

State Key Lab. of Power System (SKLD11M02).

REFERENCES

SSR W.G. (1992). Reader’s guide to subsynchronous

resonance. IEEE Trans. on Power Systems, 7(1),

150-157.

Yu, C., Cai, Z., Ni, Y., et al. (2006). Generalized

eigenvalue and complex torque coefficient analysis for

SSR study based on LDAE model．IEE Proc. Gener.

Transm. Distrib, 150(1), 25-34．

Canay I. M. (1982). A novel approach to the torsional

interaction and electrical damping of the synchronous

machine Part I: Theory． IEEE Trans. on Power

Apparatus and Systems, 101(10): 3630-3638．

Hara, T., Kobayashi, N., Takei, A., et al. (1994).

Development of a damping analysis program for

multi-generator power systems ． IEEE Trans. on

Power Systems, 9(4), 1803-1810.

Kajoijilertsakul, P., Asawasripongtorn, S., Sanposh, P., et

al. (2011). Modeling and simulation of 500 kV

transmission network for numerical fault calculation,

detection using PSCAD/EMTDC. In APPEEC, 2011

Asia-Pacific Power and Energy Engineering

Conference, 1- 4.

Xie X., Zhang X., Dong X., et al. (2011). Nonlinearity of

torsional damping and its effect on SSR characteristics

of turbine generators. In GIGRE Colloquium on New

Development of Rotating Electrical Machines,

163-170.

IEEE Committee. (1977). First benchmark model for

computer simulation of subsynchronous resonance.

IEEE Trans. on Power Apparatus and Systems, 96(1),

1565-1572.

IEEE Committee. (1985). Second benchmark model for

computer simulation of subsynchronous resonance.

IEEE Trans. on Power Apparatus and Systems,

104(5), 1057-1066.

Baker, D. H., Boukarim, G. E., D'Aquila, R. (2005).

Subsynchronous resonance studies and mitigation

methods for series capacitor applications. In PES

2005, PES Inaugural Conference and Exposition in

Africa, 386-392.

Xie X., Guo X., Han Y. (2011). Mitigation of

multimodal SSR using SEDC in the Shangdu

series-compensated power system. IEEE Trans. Power

Systems, 26(1), 384-391.

Kamwa, I., Grondin, R., Trudel G. (2005). IEEE PSS2B

versus PSS4B: the limits of performance of modern

power system stabilizers. IEEE Trans. on Power

Systems, 20(2), 903-915.

SIMULTECH 2012 - 2nd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

424