
Efficient Coupled PHY and MAC Use of Physical Bursts
in WiMAX/IEEE 802.16e Networks
Oran Sharon
1
, Gassan Tabajah
2
and Yaron Alpert
2
1
Department of Computer Science, Netanya Academic College, 1 University St., Netanya 42365, Israel
2
Intel Corporation, Haifa, Israel
Keywords:
WiMAX, Bursts, FEC Blocks, Scheduling, Goodput.
Abstract:
We address several issues related to the efficient use of Bursts in WiMAX/IEEE 802.16e systems. We look
on the relation between the PHY layer budding blocks (FEC blocks ) and the allocation of MAC level frames
(PDUs) over these FEC blocks. In particular, we show how to transmit a given amount of MAC level data bits
over a given Burst in order to maximize the number of successfully transmitted data bits in the Burst. We also
compute, given an amount of data bits to transmit, what is the Burst size that maximizes each of the following
three performance criterion: the number of successfully transmitted data bits in the Burst, the maximum ratio
between the number of successfully transmitted data bits to the Burst size, and the number of successfully
transmitted data bits per PHY slot. For the first problem the paper shows how to optimally divide the Burst
into PDUs and shows that sometimes it is more efficient to use less reliable Modulation/Coding schemes. For
the second problem the paper shows that using the PHY slots efficiently is the best criterion to consider.
1 INTRODUCTION
Broadband Wireless Access (BWA) networks consti-
tute one of the greatest challenges for the telecom-
munication industry in the near future. These net-
works fulfill the need for range, capacity, mobil-
ity and QoS support from wireless networks. IEEE
802.16e (IEEE, 2005), also known as WiMAX (
Worldwide Interoperabilityfor Microwave Access ) is
the industry name for the standards being developed
for broadband access.
IEEE 802.16e/WiMAX system is composed of a
Base Station (BS) and subscribers, denoted Mobile
Stations (MSs), in a cellular architecture. The trans-
missions in a cell are usually Point-to-Multipoint,
where the BS transmits to the subscribers on a Down-
link channel and the subscribers transmit to the BS on
an Uplink channel.
A common PHY layer used in IEEE 802.16e
is Orthogonal Frequency Division Multiple Access
(OFDMA) in which transmissions are carried in
transmission frames (IEEE, 2005). Every frame is a
matrix in which one dimension is a sub-channel (band
of frequencies) and the other dimension is time. A
cell in the matrix is denoted as a slot. The number of
data bits that can be transmitted in a slot is a function
of the Modulation and Coding scheme (MCS) that is
used in the slot.
A Burst in a frame is a subset of consecutive slots
sharing the same MCS, which is designated to a MS
for its transmission on the Uplink, or to the BS for
a transmission on the Downlink. In this paper we
assume that the Convolutional Turbo Code (CTC) is
used as the coding scheme, and in this case a Burst
also maps Forward Error Correction (FEC) blocks to
the slots. All the data bits in a FEC block have some
probability p to arrive successfully at the receiver.
The BS and the MSs transmit Protocol Data Units
(PDU) within Bursts. Within PDUs the BS and the
MSs transmit their application packets that are de-
noted Service Data Units (SDU). Each PDU has a
fixed header, denoted Generic MAC Header (GMH).
Optionally, a PDU also has a CRC field. The GMH,
CRC and other (sub)headers, not mentioned here,
within a PDU, are considered to be PDU overhead.
The probability Q that a PDU arrives correctly at
the receiver is the probability that all its bits arrive
correctly. This is also the probability that all the FEC
blocks that contain a part of the PDU arrive correctly.
Thus, if a PDU is transmitted within X FEC blocks,
and every FEC block has a success probability p, then
Q = p
X
.
In this paper we assume the transmission of a bit
stream in the PDUs, and not SDUs. The first problem
343
Sharon O., Tabajah G. and Alpert Y..
Efficient Coupled PHY and MAC Use of Physical Bursts in WiMAX/IEEE 802.16e Networks.
DOI: 10.5220/0003975003430348
In Proceedings of the International Conference on Signal Processing and Multimedia Applications and Wireless Information Networks and Systems
(WINSYS-2012), pages 343-348
ISBN: 978-989-8565-25-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

that we investigate is as follows: Given a Signal-to-
Noise-Ratio (SNR), a Burst and an amount of N data
bits to transmit in the Burst, what is the most efficient
way to allocate PDUs in the Burst so that the num-
ber of data bits that are transmitted successfully in the
Burst is maximized. In the second problem we are
given an SNR and N data bits to transmit. We look for
the optimal Burst size in relation to three performance
criterion. In the first one we look for the Burst size
that maximizes the number of successfully transmit-
ted data bits. In the second criterion we look for the
Burst size that is most efficiently used, i.e. the relation
between the number of successfully transmitted data
bits in the Burst, to the Burst size, is maximized. In
the third criterion we look for the Burst size that max-
imizes the number of successfully transmitted data
bits per transmission slot. The above problems can
arise, for example, when a MS is allocated a Burst
and wants to use it in the most efficient way, and when
the BS needs to allocate Bursts to MSs after receiving
their traffic needs. Notice that a solution to the above
problems is important in relation to a PHY layer that
is based on CTC because the Burst length determines
the FEC blocks that it contains. Next, PDUs are de-
fined over these FEC blocks. Therefore, there is a di-
rect correlation between the Burst size, the PHY layer
and the MAC layer, which influences the efficiency of
the transmissions.
The performance of IEEE 802.16e/WiMAX sys-
tems has been extensively investigated. Due to a
space limit we do not give examples for relevant stud-
ies. The interested reader can find in (So-In et al.,
2009) and (Sekercioglu et al., 2009) a very good sur-
vey on WiMAX performance. Most of the papers deal
with scheduling methods and the efficiency of trans-
port layer protocols in IEEE 802.16e systems. These
papers assume the assignment of Bursts to MSs.
However, they do not consider the issue of efficient
transmissions in the Bursts. The only works that we
are aware of, and that deal with the mutual influence
between the PHY layer budding blocks (FEC blocks)
and the MAC layer PDUs in IEEE 802.16e/WiMAX
systems are (Martikainen et al., 2008), (Alpert et al.,
2012b),(Alpert et al., 2010) and (Alpert et al., 2012a).
These papers however, handle different problems than
those in this paper.
The rest of the paper is organized as follows: In
Section 2 we answer the question of which is the most
efficient way to transmit a given amount of data bits in
a given Burst. In Section 3, given an amount of data
bits to transmit, we look for the optimal Burst sizes
according to the criterion mentioned above.
2 THE OPTIMAL
TRANSMISSION OF DATA IN A
GIVEN BURST
2.1 Problem Description
We are given an SNR, a Burst of S slots, an amount
of N data bits to transmit and the number of the PDU
overhead bits. We want to decide on the best MCS
to use in the Burst, and how to allocate PDUs in the
Burst, such that an efficiency criterion, denoted D-
Goodput, that we define next, is maximized. In Sec-
tions 2.2-2.4 we assume all the above parameters, and
also a MCS. These parameters, all together, determine
the number L of FEC blocks in the Burst, their size
F in bits and a FEC success probability p. Then, in
Sections 2.5 and 2.6 we show how to choose the best
MCS.
2.2 Definition of the D-Goodput
We are given: A Burst of L FEC blocks, every FEC
block contains F bits, every FEC block has proba-
bility p to arrive successfully at the receiver, N data
bits to transmit in the Burst and every PDU has O
overhead bits. We assume that O < F since according
to the IEEE 802.16e/WiMAX standard (IEEE, 2005),
the total length of the overheadfields in a PDU is most
likely to be smaller than one FEC block.
We want to transmit the N data bits in the Burst
such that the Data Goodput (D-Goodput) is maxi-
mized. The D-Goodput is defined as follows. Let S
be the number of data bits in the Burst, out of the N
bits, that arrive successfully at the receiver. Then: D-
Goodput =
S
N
. Notice that the D-Goodput it computed
using N in the denominator,because the Burst is given
and we want to use it to transmit to the receiver as
many data bits as possible.
Data bits are transmitted within PDUs and so we
need to decide on how many PDUs shall be allocated
in the Burst, their length and their location. We call
these decisions the division of the Burst into PDUs.
2.3 Optimal Division into PDUs
In order to find the optimal division of the Burst into
PDUs, we prove the following 5 Theorems. We omit
their proofs due to a space limit.
Theorem 1. There is an optimal division of the Burst
into PDUs such that every PDU begins and ends at
exact boundaries of FEC blocks.
Theorem 2. Assume that for a given N > L(F − O)
an optimal division of the Burst contains I PDUs. Let
WINSYS2012-InternationalConferenceonWirelessInformationNetworksandSystems
344

l be the size of the longest PDU such that l ≥ 2. Then,
it is possible to locate all the free bits in the Burst, if
such exist, in one PDU of length l.
Theorem 3. In an optimal division of the Burst into
PDUs where N > L(F − O) there are at most O− 1
free bits.
Theorem 4. In an optimal division of a Burst into
PDUs, either all the PDUs are of the same length or
the difference in length between the longest and the
shortest PDUs is one FEC block.
Theorem 5. Assume an optimal division of a Burst
into PDUs such that there are I PDUs in the divi-
sion. Then, there is only one possibility to optimally
divide the Burst into I PDUs such that the difference
in length between the longest and the shortest PDUs
is at most one FEC block.
2.4 The Optimal D-Goodput
Following Theorems 1- 5 we now show how to find
the unique division of the Burst into I PDUs such that
the difference in length between the longest and the
shortest PDUs is at most one FEC block. If I divides
L and L = I · Z then the I PDUs are all of the same
length of Z =
L
I
FEC blocks. If I does not divide L
then L = I · Z + r = (I − r) · Z + r· (Z + 1) such that
Z =
L
I
and r = L mod I, 1 ≤ r ≤ I − 1. Therefore,
the I PDUs are divided into (I − r) PDUs of Z FEC
blocks each, and r PDUs of Z + 1 FEC blocks each.
For example, for L = 13 and I = 3 we get that 13 =
3· 4+ 1 = 2· 4+ 1· 5, i.e. Z = 4 and r = 1. We get 2
PDUs of 4 FEC blocks and 1 PDU of 5 FEC blocks.
Following Theorems 1-5 Algorithm D-Goodput to
find the maximum D-Goodput is as follows:
Algorithm D-Goodput(L, F, O, p, N):
• Compute:
X
max
=
j
ln(0.8)
ln(p)
k
, I
min
=
l
L
X
max
m
, N
′
= L· F − I
min
·
O, if (N > N
′
) N ← N
′
, I
max
=
L·F−N
O
, I =
min{I
max
, L}
• Compute:
L = I · Z + r, 0 ≤ r < I.
• D-Goodput(L,F,O,p,N) =
p
L
I
r = 0
(I−r)·(F·Z−O)p
Z
N
+
[N−(I−r)·(F·Z−O)]p
Z+1
N
otherwise
In the expression above for the D-Goodput, the term
(I − r) · (F · Z − O)p
Z
denotes the contribution of the
data bits in the short PDUs to the D-Goodput. The
term [N − (I − r) · (F · Z − O)]p
Z+1
denotes the con-
tribution of the data bits in the long PDUs to the D-
Goodput.
2.5 Determining the
Modulation/Coding Scheme in the
Burst
IEEE 802.16e/WiMAX enables the use of the fol-
lowing Modulation/Coding schemes (MCSs) (IEEE,
2005): QPSK-1/2, QPSK-3/4, 16QAM-1/2, 16QAM-
3/4, 64QAM-1/2, 64QAM-2/3, 64QAM-3/4 and
64QAM-5/6.
Recall that when a Burst is defined, actually it uses
slots in the Physical layer. In any MCS the set of
slots in a Burst is divided into groups such that any
group is a FEC block. In every MCS it is possible to
define groups of slots of different sizes, resulting in
FEC blocks of different sizes. In general, the number
of FEC blocks in a given Burst, and the number of
data bits that can be transmitted in a Burst, becomes
smaller as the reliability of the MCSs increases.
It turns out that there is a trade-off in using the set
of slots of a Burst. On one hand it is possible to decide
on a reliable MCS to be used in the Burst. However,
the number of FEC blocks, and so the number of bits
in the Burst, is low. On the other hand, a less reli-
able MCS results in more FEC blocks and bits in the
Burst, but with a smaller success probability of the
FEC blocks. A question arises now: Given a number
N of data bits and a Burst of S slots, what is the best
MCS to use in the Burst such that the D-Goodput is
maximized. Due to space limits we omit numeric re-
sults for the question. In general however, it turns out
that sometimes it is more efficient to use less reliable
MCSs. There are two reasons for this outcome: First,
less reliable MCSs sometimes enable the transmission
of all the N data bits while more reliable MCSs do
not enable this transmission. Second, the larger num-
ber of bits in the less reliable MCSs enables to define
smaller PDUs, with a larger success probability than
the PDUs in more reliable MCSs. This compensates
for the smaller success probability of a single FEC
block in the former MCSs.
2.6 Summary of Results
Combining the discussion in Section 2.5 together with
Algorithm D-Goodput from section 2.4 and given an
SNR, a Burst of S slots and an amount of N data bits
to transmit, the following procedure should be used in
order to maximize the D-Goodput:
1. For every MCS applicable in the given SNR:
EfficientCoupledPHYandMACUseofPhysicalBurstsinWiMAX/IEEE802.16eNetworks
345

1.1. Compute the number of FEC blocks in the
Burst L, their size F and their success probability
p.
1.2. If (L · F − I
min
· O − N < 0) then it is not
possible to transmit the given N data bits in the
Burst. Otherwise, compute the D-Goodput by Al-
gorithm D-Goodput (I
min
is taken from Algorithm
D-Goodput).
2. Choose the MCS that yields the largest D-
Goodput, if such exists.
Remark: if there is no MCS in which it is possible
to transmit all the data bits, then one can reduce this
number as it is shown in Algorithm D-Goodput.
3 THE OPTIMAL BURST SIZE
FOR DATA TRANSMISSION
In this section we are given an SNR, an amount of N
data bits to transmit and the number of the PDU over-
head bits. We are looking for the optimal Burst size
to transmit these data bits. We suggest 3 possible per-
formance criterion, and for each criterion we decide
on the best MCS to use in the given SNR and on the
optimal Burst size.
The first performance criterion is Max-Bits which
maximizes the number of successfully transmitted
data bits in the Burst. The second criterion is Burst-
Goodput that maximizes the ratio between the num-
ber of successfully transmitted data bits in the Burst,
to the Burst size. The third criterion, Slot-Goodput,
maximizes the number of successfully transmitted
data bits per transmission slot.
When we consider a MCS in the given SNR, we
are actually being given a FEC block size F and a
FEC block success probability p. This probability is
determined by the given SNR. Thus, for every MCS
the input we have is: N data bits to transmit in a Burst,
FEC blocks that contain F bits each, every FEC block
has probability p to arrive successfully at the receiver,
and every PDU has O overhead bits. O < F from the
same reasons as in Section 2.
For each of the performance criterion we look for
the Burst size that maximizes the criterion in the con-
sidered MCS. Then, the MCS in which the best re-
sult is achieved, is the one to use in the given SNR.
Finally, we compare between the three criterion. The
outcome is that using the Slot-Goodput criterion is the
best since on one hand it enables the transmission of
data bits almost as Max-Bits, but on the other hand it
uses much less resources.
3.1 The Max-bits Criterion
In this section we look for the Burst size that maxi-
mizes the number of successfully transmitted data bits
in a Burst. Consider a Burst of L
max
FEC blocks such
that L
max
=
N
F−O
. With this number of FEC blocks
in a Burst, every FEC block is a separate PDU, and
the number of successfully transmitted data bits in the
Burst is N · p. Clearly, this is the maximum possible.
Given an SNR, the MCS with the highest FEC
block success probability p is the best to use.
3.2 The Burst-Goodput Criterion
3.2.1 Finding the Shortest and Longest Burst
Sizes
In this section we look for the Burst size that is most
efficiently used. In other words, we want to maximize
the Burst Goodput (B-Goodput) that is defined as fol-
lows. Let S be the number of data bits, out of the
N bits, that are successfully transmitted in a Burst.
Let B be the length of the Burst in bits. Then, the B-
Goodput is defined as B-Goodput=
S
B
. In this section
we are looking for the optimal number of FEC blocks,
L, such that
S
B
=
S
L·F
is maximal.
Notice that the Burst size in this case is not an
input to the problem, and we look for the Burst that is
most efficiently used. Therefore, the denominator of
the B-Goodput is the Burst size.
First recall the value L
max
such that L
max
=
N
F−O
. With this number of FEC blocks in a Burst,
one can define every FEC block to be a separate PDU.
In this case the B-Goodput is
N·p
B
. Using more FEC
blocks only enlarges the denominator but the numer-
ator remains the same. Therefore, there is no merit to
consider Bursts with more than L
max
FEC blocks.
We now compute L
min
, the minimum number of
FEC blocks that are needed to transmit the N bits. We
want the success probability of a PDU to be at least
0.8 and so the maximal number of FEC blocks in a
PDU is X
max
=
j
ln(0.8)
ln(p)
k
. We now compute L
min
by
defining X
1
and X
2
as follows:
1. X
1
=
j
N
X
max
·F−O
k
. X
1
is the number of PDUs of
length X
max
FEC blocks that is needed for the
transmission of the N data bits.
2. X
2
=
l
N−X
1
·(X
max
·F−O)+O
F
m
·
l
N−X
1
·(X
max
·F−O)
N−X
1
·(X
max
·F−O)+O
m
.
X
2
< X
max
and it is the number of FEC blocks in a
PDU that contains the remaining data bits that are
not transmitted in a PDU of length X
max
.
Also notice that if all the N bits can be transmitted in
one PDU of length smaller than X
max
then X
1
= 0.
WINSYS2012-InternationalConferenceonWirelessInformationNetworksandSystems
346

Then, L
min
is given by :
L
min
= X
1
· X
max
+ X
2
3.2.2 Finding the Optimal Burst Size
From Section 3.2.1 we can conclude that the optimal
L is between L
min
and L
max
. For a given L the B-
Goodput can be computed by Algorithm D-Goodput
in Section 2.4, except that the denominator N in the
expression for the D-Goodput is replaced by L· F.
The following algorithm, Compute L-Goodput,
computes the maximum B-Goodput for a given
L, L
min
≤ L ≤ L
max
− 1:
Compute L-Goodput(L, F, O, p, N):
• Compute:
I =
L·F−N
O
, L = I · Z + r, 0 ≤ r < I.
• B-Goodput(L,F,O,p,N) =
N·p
L
I
L·F
r = 0
(I−r)·(F·Z−O)p
Z
L·F
+
[N−(I−r)·(F·Z−O)]p
Z+1
L·F
otherwise
The B-Goodput for L = L
max
is always
N·p
L
max
·F
.
Therefore, we now define Algorithm B-Goodput that
computes the optimal Burst size given F, O, p, N.
Algorithm B-Goodput(F,O,p,N):
1. Compute:
L
max
=
N
F−O
, X
max
=
j
ln(0.8)
ln(p)
k
, X
1
=
j
N
X
max
·F−O
k
, X
2
=
l
N−X
1
(X
max
·F−O)+O
F
m
·
l
N−X
1
·(X
max
·F−O)
N−X
1
·(X
max
·F−O)+O
m
, L
min
= X
max
· X
1
+ X
2
,
MaxGoodput = 0, OptimalL = NIL
2. For every L
min
≤ L ≤ L
max
− 1 if Compute L −
Goodput(L, F,O, p, N) > MaxGoodput
then { MaxGoodput = Compute L −
Goodput(L, F,O, p, N);OptimalL = L }.
3. If
N·p
L
max
·F
> MaxGoodput then { MaxGoodput =
N·p
L
max
·F
;OptimalL = L
max
}.
4. return(OptimalL, MaxGoodput)
3.2.3 Determining the Modulation/Coding
Scheme in the Burst
The question of which is the best MCS to use, given
an SNR, in order to receive the maximum B-Goodput
depends on F,O,p and N. We do not have a closed
term for the B-Goodput and so one needs to check all
the applicable MCSs.
3.3 The Slot-Goodput Criterion
3.3.1 The Criterion Definition
In this section we define another performance crite-
rion, denoted Slot-Goodput. This criterion counts,
given a Burst and a MCS, the number of successfully
transmitted data bits per slot. Or, in other words, we
measure the contribution of the physical resource di-
rectly.
Given an SNR and a MCS, i.e. F and p, the num-
ber N of data bits to transmit and the number of PDU
overhead bits O, the sizes of the possible Bursts are
limited, as before, by L
min
and L
max
. The optimal L is
computed by Algorithm B-Goodput since the differ-
ence between the B-Goodput and the Slot-Goodput is
by a constant factor,
F
j
, where j is the number of slots
in a FEC block.
3.3.2 Determining the Modulation/Coding
Scheme in the Burst
Same as in the Burst-Goodput criterion.
3.4 Comparison between the
Performance Criterion
The Max-Bits performance criterion maximizes the
number of successfully transmitted data bits in a
Burst. Therefore, from a single user perspective, it
is the best one. However, this criterion consumes
many resources because it uses many FEC blocks.
This can lead to un-fairness among users if the sys-
tem resources are limited. Therefore, if the system
is not overloaded, the Max-Bits criterion is applica-
ble. However, if the system is overloaded, the Slot-
Goodput criterion shall be used because it uses the
transmission slots in the most efficient way, as we
show next.
In Figures 1 and 2 we check the following for two
SNR values and different values of N: Given an SNR
and N, we compute the optimal Burst size accord-
ing to each of the three performance criterion. Then,
for each such Block size we compute the number of
successfully transmitted data bits, and the number of
transmission slots that such a Burst occupies. No-
tice that in order to find the optimal Burst size for
the Burst-Goodput and for the Slot-Goodput criterion,
given an SNR and N, we check all the applicable
MCSs, and choose the best among them.
From Figure 1 it turns out that using the optimal
Burst sizes according to the Burst-Goodput and the
Slot-Goodput criterion does not reduce significantly
EfficientCoupledPHYandMACUseofPhysicalBurstsinWiMAX/IEEE802.16eNetworks
347
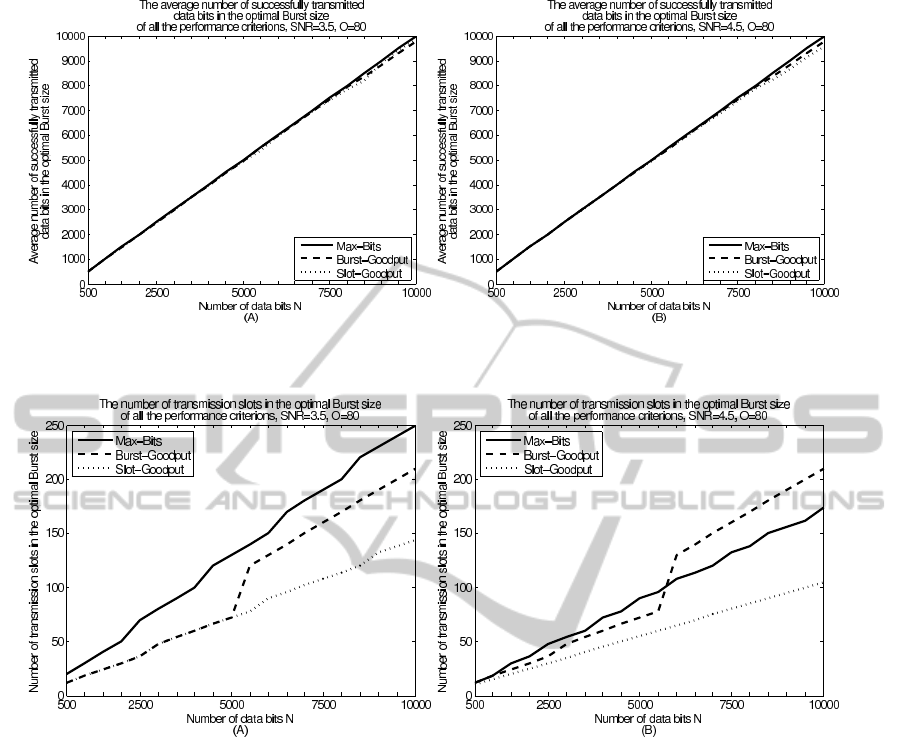
Figure 1: The number of successfully transmitted data bits in the optimal Burst size of the various performance criterion, for
various SNRs(dB) and for a various number of data bits, O = 80 bits.
Figure 2: The number of slots in the optimal Burst size of the various performance criterion, for various SNRs(dB) and for a
various number of data bits, O = 80 bits.
the number of successfully transmitted data bits, com-
pared to the optimal Burst size of the Max-Bits crite-
rion. On the other hand, from Figure 2 one can see
that the saving in the number of the transmission slots
is very significant. Therefore, the Slot-Goodput is the
most attractive performance criterion to use.
REFERENCES
Alpert, Y., Segev, J., and Sharon, O. (2010). Advanced cou-
pled phy and mac scheduling in ieee 802.16 wimax
systems. Physical Communication, 3:287–298.
Alpert, Y., Segev, J., and Sharon, O. (2012a). Coupled phy,
mac and repetition in ieee 802.16 wimax systems. To
be published, Physical Communication.
Alpert, Y., Segev, J., and Sharon, O. (2012b). Towards an
optimal transmission of sdus by msc in ieee 802.16
wimax systems. Submitted, Physical Communication.
IEEE (2005). IEEE 802.16e, Part 16: Air Interface for
Fixed and Mobile Broadband Wireless Access Sys-
tems. IEEE Standards for Local and Metroplitan Area
Networks.
Martikainen, H., Sayenko, A., Alanen, O., and Tykomy-
rov, V. (2008). Optimal mac pdu size in ieee 802.16.
In Telecomunication networking Workshop on QoS in
Multiservice IP Networks, pages 66–71.
Sekercioglu, Y. A., Ivanovich, M., and Yegin, A. (2009).
A survey of mac based qos implemetation for wimax
networks. Computer Networks.
So-In, C., Jain, R., and Tamami, A. K. (2009). Schedul-
ing in ieee 802.16e mobile wimax networks: Key is-
sues and a survey. IEEE Journal on Selected Areas in
Communication, 27.
WINSYS2012-InternationalConferenceonWirelessInformationNetworksandSystems
348
