
Reversible Steganographic Scheme with High Embedding Capacity
using Dual Cover Images
Nagaraj V. Dharwadkar and B. B. Amberker
Department of Computer Science and Engg., National Institute of Technology, Warangal, 506004, India
Keywords:
Reversible, Steganography, Dual Cover Images, Embedding Capacity, Stegoimage, Stego-key, Secret
Communication.
Abstract:
The advances in Internet technology and digital image representation helped the user to easily exchange the
secret message. On Internet the transmission of the secret message is conducted using digital images which
created new needs, issues and opportunities to the researcher. The basic objective of secret message commu-
nication is to transmit a message securely by embedding it into a cover-image such that unintended observers
are unable to detect it. The image steganographic schemes are used in secret message communication. In
this paper, we have proposed reversible steganographic scheme for gray-scale images. This scheme uses dual
cover images to hide secret image and generates the perceptually similar dual stegoimages. Further, to extract
the secret image the knowledge of dual stegoimages and stego-key are necessary which improved the security
of this scheme. The experimental results show that the scheme provides a higher embedding capacity and
robustness with un-noticeable distortions in the stegoimages. The performance of the scheme is analyzed for
various types of image processing attacks on stegoimage. The proposed scheme was found rigid to the image
processing attacks.
1 INTRODUCTION
In many countries of the world the political dissent
is not tolerable and illegal. Hence, to exchange the
secret messages the dissident organization must exer-
cise extreme caution (Nagaraj V. Dharwadkar, 2010).
The dissidents always use the Internet to exchange
secret messages and face the security threats (Zou
et al., 2003). To conceal secret communications
the dissidents may use encryption or steganography
methods. Using encryption the dissidents will en-
sure the privacy of their communications. Unfortu-
nately, the very important fact is that two people are
exchanging encrypted messages indicates that they
have something to conceal. An alternate solution to
this problem is the use of steganography for secret
communication(Lee and Chen, 2000a; Katzenbesser
and Petitcolas, 2004; Artz, 2001). Steganography is
the art of hidden writing. First documented exam-
ple of steganography was found in the Histories of
Herodotus, where the father of history relates sev-
eral stories from the times of ancient Greece (Kahn,
1967). There are stories of secret messages written
in invisible ink or hidden in letters such that the first
character of each sentence is used to spell a secret
message (Cox et al., 2008). In recent days, digital
steganographic schemes are widely used by prison-
ers, spies, terrorists and soldiers. Most of the recent
secret communications occurs electronically, where
the digital multimedia representations techniques are
used as the carrier for secret communication (W et al.,
1996). The Internet is increasingly becoming the pop-
ular communication channel for secret communica-
tion. The image Steganographic schemes are widely
used in the transmission of secret messages via the
Internet to provide secured communication (Artz.,
2001; Lee and Chen, 2000b).
In 2001, T. Sharp (Sharp, 2001) proposed one bit
LSB substitution scheme. In this scheme the secret
message is embedded into cover image by substitut-
ing the LSB of each pixel with encrypted secret bit
stream. Only the authorised receiver will extract the
secret bits by decrypting every LSB of pixel of the
cover image using a shared key. The embedding ca-
pacity of this scheme is 1 bit/pixel. This scheme gen-
erates visually imperceptible stegoimage which can
be statistically analyzed by unauthorised entity with-
out knowledge of the shared key. The random LSB
bit jumbling attack on stegoimage makes it difficult
to extract the secret message. To address this prob-
15
V. Dharwadkar N. and B. Amberker B..
Reversible Steganographic Scheme with High Embedding Capacity using Dual Cover Images.
DOI: 10.5220/0003975700150024
In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2012), pages 15-24
ISBN: 978-989-8565-24-2
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

lem, A. Ker (Ker, 2005) proposed the LSB match-
ing scheme, but this scheme is vulnerable to detec-
tion algorithms. In order to minimize the effect of
detectability Rehab H. (Alwan et al., 2006) proposed
a novel scheme of image embedding which detects
the edge of the image using Sobel mask filters. On
the LSB of each edge pixels, a gray level connectiv-
ity is applied using fuzzy logic and the ASCII code
information is embedded into the edge pixels. The
well known steganographic scheme is Least Signifi-
cant Bit (LSB) substitution scheme. This scheme di-
vides the secret message into n bit blocks and em-
beds each of these n bits by directly replacing the
n LSBs of a pixel of the cover image (Wang et al.,
2001; Thien and Lin, 2003). Using LSB substitution
schemes, more number of secret bits can be hidden
into cover image with low computational complex-
ity (Chan and Chen, 2004; Nagaraj V. Dharwadkar,
2010). Based on the ability of the steganographic
schemes to recover the cover images during extrac-
tion, the schemes are classified as reversible (Hon-
singer et al., 2001; Fridrich et al., 2002; Tian, 2003)
and irreversible(Chan and Cheng, 2004; Mielikainen,
2006). The reversible steganographic schemes are
able to recover the original cover image during ex-
traction of the secret message; where as in the irre-
versible steganographic scheme the secret message is
extracted from the stegoimages with no capability of
recovering the cover image into its original state.
The embedding capacity, visual quality and secu-
rity are three important issues concerned to a success-
ful steganographic schemes (Wang et al., 2001). The
crucial issue of the steganographic scheme is rigidity
of scheme to different types of attacks. To address is-
sues like embedding capacity, visual quality and secu-
rity of stegoimage, Chin-Feng et.al.(Lee et al., 2009).
In 2010, to address similar issues we have proposed
a scheme (Nagaraj V.Dharwadkar, 2010) which is an
improved reversible steganographic scheme based on
dual stegoimages. In Chin-Feng et.al. scheme, a max-
imum of two secret bits are embedded into a pair of
pixels which are originated from one original cover
image and its copy. This scheme achieves an embed-
ding capacity of 0.75 bpp. Where as the earlier pro-
posed our scheme embeds the three secret bits into
pair of pixels (Nagaraj V.Dharwadkar, 2010). This
scheme achieves an embedding capacity of 1.21 bpp.
This scheme is purely blind scheme and it will not use
any auxiliary array in extraction algorithm.
After analysing these schemes it was found that
the embedding capacity of these scheme can be pos-
sible to further increase using auxiliary array. To
achieve the high embedding capacity, in this paper
we propose an improved reversible steganographic
scheme using two cover images. In this scheme,
five bits of secret image are embedded into a pixel
pair which are alternatively selected from the orig-
inal cover image and its copy. We have used aux-
iliary array known as stego-key which increases the
embedding capacity and security of the scheme. This
scheme provides reversibility and high security with
less distortion in stegoimage. We have analyzed the
proposed scheme for its embedding capacity and its
robustness to different types of image processing at-
tacks.
The rest of the paper is organized as follows. The
proposed steganographic scheme is explained in Sec-
tion 2. Section 3 gives details of the experimental re-
sults. Section 4 gives the comparison of the proposed
scheme with the Chin-Feng Lee et. al and our own
earlier proposed scheme. The effect of image pro-
cessing attacks on dual stegoimages is discussed in
Section 5. Section 6 concludes the paper.
2 PROPOSED SCHEME
In the gray-scale image the intensity value of pixel
is represented by 8 bits value. The proposed scheme
relies on binary stream of intensity of pixel to de-
fine space for embedding the secret bits. We con-
sider two identical cover images P and Q each of
size m × n. In Figure 1, the cover images P and Q
are represented as a matrices (P
i, j
)
1≤i≤m;1≤ j≤n
and
(Q
i, j
)
1≤i≤m;1≤ j≤n
. For embedding data we choose
a pair of pixels (P
i, j
,Q
i, j
) each from P and Q. If
P
i, j
is used for embedding secret, then P
i, j
is re-
ferred as the Embed pixel and Q
i, j
is referred as the
Ref pixel. For the next pair (P
i+1, j
,Q
i+1, j
), P
i+1, j
is Ref pixel and Q
i+1, j
is Embed pixel. Likewise,
pair of pixels are chosen row-wise from each cover
image P and Q. The proposed scheme embeds five
bits into a pair of pixels by maintaining the negligi-
ble difference between the original pixel and modi-
fied pixel. To achieve negligible difference the mod-
ified pixel is scaled up or down. The scale factors
which are used to preserve the difference narrow is
encoded in a location-map which is known as stego-
key. The hidden message is encoded in two places
: the image and the location-map. The secret bits
S
k
are selected and embedded into Embed pix
k
for
0 ≤ k ≤ 4 using look-up table as shown in Figure
2 to generate resultant Res pix.Later, the difference
d = Embed pix− Res pix is computed. If the differ-
ence |d| > 3 and d > 0 and to make Res pix equal
to Embed pix 4 is added count number of times and
stored in Res pix. Otherwise if d < 0 to make Res pix
equal to Embed pix 4 is subtracted count number of
SECRYPT2012-InternationalConferenceonSecurityandCryptography
16

times and stored into Res pix. Store the count in to
Stego− key element such that the LSB of Stego− key
element represents addition or subtraction operation.
The remaining bits represents the count value. The
embedding algorithm is given in Algorithm : 1 and
continued in Algorithm : 2.
(a) Cover image P. (b) Cover image Q.
Figure 1: Selection of alternate pixels from dual cover im-
ages P and Q where P = Q.
In extraction algorithm consider two embedded
images P
′
and Q
′
each of size m × n. From the em-
bedded image P
′
and Q
′
we choose a pair of pixels
(P
′
i, j
,Q
′
i, j
) each from P
′
and Q
′
. If P
′
i, j
is used for ex-
tracting secret, then P
′
i, j
is assigned to the Embed pix
and Q
′
i, j
is assigned to the Ref pixel. For the next
pair (P
′
i+1, j
,Q
′
i+1, j
), P
′
i+1, j
is Embed pixel and Q
′
i+1, j
is Ref pixel. Likewise, pair of pixels are chosen row-
wise from each stegoimage image P
′
and Q
′
. This
scheme extracts five bits from pair of pixels using the
location-map known as the stego-key. The stego-key
content is used to decide the scale factor by which the
embedded pixel values to be increased or decreased.
The altered embedded pixel and reference are used
to recover the hidden data.The original cover pixel is
recovered from the reference pixel. The extraction al-
gorithm is given in Algorithm: 3 and 4.
2.1 Illustration with Example
Let’s explain the scheme with a simple example.
Assume that we have two cover images I
1
, I
2
of size
3× 3, where I
1
= I
2
and secret image S of size 4× 4
I
1
= I
2
=
20 5 9
1 7 15
37 2 52
S =
0 0 0 0
1 1 1 0
1 0 1 1
0 0 1 0
The execution of embedding steps for cover image
I
1
,I
2
and secret image S will generate the following
output: Select the pixel p
1
1
= 20 = (00010100)
2
of cover image I
1
and 00001 the first 5 bits of
S. Using look-up table as given in Figure 2 we
Figure 2: Look-up table used to map the cover image pixels
into stegoimages.
get r = (00011110) = 30 as modified pixel. The
difference |d| = |p
1
1
− r| = |20 − 30| = 10 is cal-
culated. As |d| > 3 r = r − 4 = 26 and set c
0
= 1.
Iteratively we calculate |d| = |p
1
1
− r| = |20− 26| = 6
until |d| > 3 therefore we get r = 26 − 4 = 22.
Then, we calculate |d| = |p
1
1
− r| = |20 − 22| = 2,
|d| < 3 therefore q
1
1
= r = 22. Thus, in this com-
plete iterations as 4 is subtracted 2 times we get
(c
3
,c
2
,c
1
) = (0,1,0) as the first element of stego-
key. Consider next pixel p
2
2
= 5 = (00000101)
2
from I
2
and next 5 bits (11010)
2
of S. Us-
ing look-up table we get r = (00000101)
2
= 5,
|d| = |p
2
2
− r| = |5 − 5| = 0 and |d| < 3 therefore
c0 = 0 and (c
3
,c
2
,c
1
)=(0,0, 0) as the next element of
stego-key. Then the pixel p
1
3
= 9 = (00001001)
2
is
selected from I
1
, next 5 secret bits (11001)
2
from S.
We get r = (00000110)
2
= 6. Compute the difference
|d| = |p
1
3
− r| = |9 − 6| = 3 therefore c
0
= 0 and
(c
3
,c
2
,c
1
) = (0,0, 0) will be the next element of
stego-key. The remaining secret bit in S is 0 and pixel
p
2
4
= 1 = (00000001)
2
, using look-up table we get
r = (00000001)
2
= 1 and |d| = |p
2
4
− r| = |1− 1| = 0.
As |d| < 3 therefore append 0 to stego-key. The
resultant stegoimages are I
′
1
=
22 5 6
1 7 15
37 2 52
,
I
′
2
=
20 5 9
1 7 15
37 2 52
and Stego-
key=(0101,0000,0000,0)
2
The execution of extraction steps on dual stegoim-
ages I
′
1
, I
′
2
using Stego-keywill generate the following
output: I
′
1
=
22 5 6
1 7 15
37 2 52
,
I
′
2
=
20 5 9
1 7 15
37 2 52
and Stego-
key=(0101,0000,0000,0)
2
Select the first pixel
from cover image p
1
1
= 22 from I
′
1
and first 4 bits
of Stego-key (c
3
,c
2
,c
1
,c
0
) = (0,1,0,1). From
the bits of first stego-key element we separate
c
0
bit to get (c
3
,c
2
,c
1
) = (0,1,0) = 2 & c
0
= 1.
As c
0
= 1 hence we need to add 4 twice to p
1
1
.
Thus, we get r
′
= 22 + 4 + 4 = 30 = (00011110)
2
.
ReversibleSteganographicSchemewithHighEmbeddingCapacityusingDualCoverImages
17

Matching the 5 LSB bits of the reference pixel
p
2
1
= 20 = (00010100)
2
and look-up table we get
(00001)
2
as the first five secret bits. Select the next
pixel p
2
2
= 5 = (00000101) from I
′
2
and next 4 bits
of Stego-key element (c
3
,c
2
,c
1
,c
0
) = (0, 0,0,0).
We get (c
3
,c
2
,c
1
) = (0,0, 0) = 0 & c
0
= 0. Using
reference pixel p
1
2
= 5 = (00000101)
2
and look-up
table we get secret bits (11010)
2
. Select the next
pixel p
1
3
= 6 = (00000110)
2
from I
′
1
and 4 bits
of Stego-key element. Using the reference pixel
p
2
3
= 9 = (00001001)
2
we get secret bits (11001)
2
.
Select the last pixel p
2
4
= 1 = (00000001)
2
from I
′
2
and stego-key element value is c
0
= 0. using the
reference pixel p
1
4
= 1 = (00000001)
2
and look-up
table we get 0 as the secret bit.
3 RESULTS AND DISCUSSION
For the experimental analysis, we implemented the
proposed scheme using JAVA package. In the series
of experiments, the perceptual quality of stegoimage
is measured using Peak Signal to Noise (PSNR) and
Mean Square Error (MSE) between the two stegoim-
ages and cover image respectively. The experimental
values of PSNR and MSE between stegoimages and
cover image shows that both stegoimage are percep-
tually similar to cover image. In order to analyze the
embedding capacity of the proposed scheme, we con-
sidered different secret images for embedding on dif-
ferent cover images. The experimental setup used in
measuring perceptual quality and embeddingcapacity
are explained in the following sections. For the ex-
perimental determination of the embedding capacity,
we considered the Lena, Peppers, Baboon and Chess-
board images of size 300× 420, 225×225, 250×250
and 256×256 respectivelyas shown in Figure 3. Four
different monochrome secret images of different sizes
are used in the embedding algorithm. Figure 4 and
Figure 5 show the dual stegoimages generated by pro-
posed scheme. Figure 6 to Figure 9 show the orig-
inal monochrome secret image and extracted secret
images from Lena, Peppers, Baboon and Chessboard
cover images.
3.1 Perceptual Quality of Stegoimages
Table 1 shows the perceptual quality measures be-
tween cover image and the stegoimages. For each
cover image, the amount of noise added into the ste-
goimage is calculated by using PSNR and MSE be-
tween cover image and both stegoimages using fol-
lowing equation.
Algorithm 1: Embedding Algorithm.
Input : Grayscale image I
1
of size m× n and its
copy I
2
, where I
1
= {p
1
1
, p
1
2
,..., p
1
m×n
},
I
2
= {p
2
1
, p
2
2
,..., p
2
m×n
}, I
1
= I
2
and secret
image S of size h× w, where
S = {s
1
,s
2
,...,s
h×w
} and s
k
∈ {0,1}
Output: Dual stegoimages, I
′
1
= {q
1
1
,q
1
2
,...,q
1
m×n
}
and I
′
2
= {q
2
1
,q
2
2
,...,q
2
m×n
} such that I
′
1
6= I
′
2
and stegokey of size (4× h× w)/5, where
C = {C
0
,C
1
,...,C
(4×h×w)/5
− 1},
C
t
= {c
3
,c
2
,c
1
,c
0
} and c
k
∈ {0,1}
1. Set i=1; k=1; x = h× w; t=0; ;
2. Set Embed pixel = p
1
i
; Ref pixel = p
2
i
;
3. if (x < 5) then goto step 8
else Set x=x-5; Count=0; r = Embed pixel;
{b
7
,b
6
,b
5
,b
4
,b
3
,b
2
,b
1
,b
0
} = (Embed pixel)
2
.
Secret bits {s
k
,s
k+1
,s
k+2
,s
k+3
,s
k+4
} ∈ S are embed
into r using the following steps ;
4. for j ← 0 to 4 do
Switch(b
j
,s
k+4− j
)
Case(0,0) : r
j
= 1;break;
Case(0,1) : r
j
= 0;break;
Case(1,0) : r
j
= 1;break;
Case(1,1) : r
j
= 0;break;
5. Compute d = Ref pixel −r
6. if (|d| ≤ 3) then q
1
1
= r goto step 7
if (|d| > 3 & d > 0) then r = r+ 4;
Count = Count + 1; flag = 1; goto step 5
if (|d| > 3 & d < 0) then r = r − 4;
Count = Count + 1; flag = 0; goto step 5
7. Indicate the modification of r into stego-key
C
t
= {c
3
,c
2
,c
1
,c
0
} using following steps.
(a) if ( f lag == 1) then c
0
= 0
(b) if ( f lag == 0) then c
0
= 1
(c) The remaining bits c
3
,c
2
,c
1
are assigned using
following cases: Switch(Count)
Case0 : (c
3
,c
2
,c
1
) = (0,0,0) break;
Case1 : (c
3
,c
2
,c
1
) = (0,0,1) break;
Case2 : (c
3
,c
2
,c
1
) = (0,1,0) break;
Case3 : (c
3
,c
2
,c
1
) = (0,1,1) break;
Case4 : (c
3
,c
2
,c
1
) = (1,0,0) break;
Case5 : (c
3
,c
2
,c
1
) = (1,0,1) break;
Case6 : (c
3
,c
2
,c
1
) = (1,1,0) break;
Case7 : (c3,c2,c1) = (1,1, 1) break;
8. Set i = i+ 1; k = k+ 5 x = x− 5;t = t +1;
9. if (i%2 == 1) then goto step 3;
else Set Embed pixel = p
2
i
and Ref pixel = p
1
i
,
Select next five secret bits (s
k
,s
k+1
,s
k+2
,s
k+3
,s
k+4
)
from S and repeat step 3 to step 7.
MSE =
∑
M
i=1
∑
N
j=1
(C[i, j] − I[i, j])
2
MN
(1)
Here, M and N are the height and width of image
respectively. C(i, j) is the (i, j)
th
pixel value of the
SECRYPT2012-InternationalConferenceonSecurityandCryptography
18

Algorithm 2: Embedding Algorithm continued.
10 if (x < 5) then Embed pixel = p
2
i
convert it into
binary stream {b
7
,b
6
,b
5
,b
4
,b
3
,b
2
,b
1
,b
0
} and
select x secret bits from S and Count1=0;
a for j ← 0 to x− 1 do
Switch(b
j
,s
k+4− j
)
Case(0,0) : r
j
= 1;break;
Case(0,1) : r
j
= 0;break;
Case(1,0) : r
j
= 1;break;
Case(1,1) : r
j
= 0;break;
b Compute d
′
= Ref pixel − r;
if (|d
′
| ≤ 3) then q
1
1
= r goto step c
if (|d
′
| > 3 & d
′
> 0) then r = r+ 4;
Count1 = Count1+ 1; flag = 1; goto step b
if (|d
′
| > 3 & d
′
< 0) then r = r− 4;
Count1 = Count1+ 1; flag = 0; goto step b
c Indicate the modification of r into stegokey using
following steps.
if (x == 1) then C
t
= {c
0
};c
0
= 0;
if (x == 2) then C
t
= {c
0
};c
0
= 1;
if (x == 3)&( flag == 1) then
C
t
= {c
1
,c
0
};c
0
= 0;c
1
= 1;
if (x == 3)&( flag == 0) then
C
t
= {c
1
,c
0
};c
0
= 1;c
1
= 1;
if (x == 4)&( flag == 0) then c
0
= 1; if
(x == 4)&( flag == 1) then c
0
= 0;
Switch(Count1) Case0 : (c
2
,c
1
) = (0, 0)
Case1 : (c2, c1) = (0,1) Case2 : (c2,c1) = (1,0)
Case3 : (c2, c1) = (1,1)
(a) Lena. (b) Baboon. (c) Peppers. (d) Chessboard.
Figure 3: Cover Images.
(a) Lena. (b) Baboon. (c) Peppers. (d) Chessboard.
Figure 4: Stegoimage1 generated by proposed scheme.
cover image and I(i, j) is the (i, j)
th
pixel value of
stegoimage.
PSNR = 10log
(2
n
− 1)
2
MSE
(2)
Where n is the number of bits used for color represen-
(a) Lena. (b) Baboon. (c) Peppers. (d) Chessboard.
Figure 5: Stegoimage2 generated by proposed scheme.
(a) Original Secret
image.
(b) Extracted Secret
image.
Figure 6: Secret image used in Lena cover image.
(a) Original Secret
image.
(b) Extracted Secret
image.
Figure 7: Secret image used in Baboon cover image.
(a) Original Secret
image.
(b) Extracted Secret
image.
Figure 8: Secret image used in peppers cover image.
(a) Original Secret
image.
(b) Extracted Secret
image.
Figure 9: Secret image used in chessboard cover image.
tation. From these experimental results it was found
that the PSNR between the stegoimage and cover im-
age is in the range of 44 to 46 dB, which is the nearest
to the PSNR value of the perceptual images consider-
ing the Human Visual System.
The quality of extracted secret image is measured
by taking four different cover images. The qual-
ity measures like Normalized Cross Correlation (NC)
and Standard Correlation (SC) are calculated between
extracted image and secret image using following
equations.
(3)
SC =
∑
M
i=1
∑
N
j=1
(I[i, j] − I
′
)(J[i, j] − J
′
)
q
∑
M
i=1
∑
N
j=1
(I[i, j] − I
′
)
q
∑
M
i=1
∑
N
j=1
(J[i, j] − J
′
)
ReversibleSteganographicSchemewithHighEmbeddingCapacityusingDualCoverImages
19

Table 1: The PSNR and MSE between the cover image and stegoimage.
Properties Lena Baboon Peppers Chessboard
Size of cover image 300× 420 250× 250 225× 225 256 × 256
Size of secret image 1000× 630 625× 500 625× 405 1280× 256
MSE between 1.65 1.74 1.74 2.24
cover & stegoimage1
PSNR between 45.93 45.72 45.70 44.62
cover & stegoimage1 (dB)
MSE between 1.67 1.75 1.73 2.24
cover & stegoimage2
PSNR between 45.88 45.69 45.74 44.62
cover & stegoimage2 (dB)
Here, I(i, j) is original secret image, J(i, j) is ex-
tracted secret image, I
′
is the mean of original secret
image and J
′
is mean of extracted secret image.
NC =
∑
M
i=1
∑
N
j=1
(I[i, j]I
′
[i, j])
∑
M
i=1
∑
N
j=1
(I[i, j])
2
(4)
Where I(i, j) is original secret image and I
′
(i, j) is ex-
tracted secret image, M is height of image and N is
width of image. Table 2 shows the NC and SC be-
tween extracted and original secret images for differ-
ent cover images. The experimental results show that
the NC and SC for all images are equal to 1 which
show that the extracted secret image is completely
correlated to the original secret image.
3.2 Embedding Capacity
In steganography the most important issue is achiev-
ing higher embedding capacity. The embedding ca-
pacity of the cover image is the number of secret
bits that can be embedded into a cover image (Na-
garaj V.Dharwadkar, 2010). The embedding capacity
is measured as bits per pixel (bpp). The embedding
capacity of image of size m× n is calculated as
C =
|T|
mn
(5)
where |T| is the total number of secret bits embedded
into cover image of size m × n. Equation (5) is used
when the scheme uses only one cover image. Since
our proposed scheme uses dual cover images, each of
size m× n, we calculate the embedding capacity as
C =
|T|
2mn
(6)
To estimate the embedding capacity of proposed
scheme, consider two cover images C
1
and C
2
each of
size m× n such that C
2
is copy of C
1
. Assume hat all
distinct consecutive pairs of pixels are embeddable.
Under these assumptions we estimate the embedding
capacity achieved by proposed scheme. There are
(mn)/2 embeddable pairs of pixels in each cover im-
age C
1
and C
2
. So there are mn pairs of pixels among
two cover images. The proposed scheme embeds 5
secret bits into pair of pixels. Thus, the total number
of secret bits that can be embedded is 5mn. According
to (5), the embedding capacity is
C =
5mn
2mn
=
5
2
= 2.5 (7)
From the experimental results we found all pairs of
pixels are embeddable and proposed scheme achieves
on average an embedding capacity of 2.5 bpp.
4 COMPARISON
We can compare our proposed scheme with T Sharp,
Chin-Feng steganographic schemes and our own ear-
lier proposed scheme (Nagaraj V.Dharwadkar, 2010).
The steganographic schemes proposed by T. Sharp
and Chin-Feng achieve an embedding capacity of 1
bpp and 0.75 bpp respectively. Where as our earlier
proposed improved reversible steganographic scheme
using dual images can able to achieve an embedding
capacity of 1.12 bpp. The earlier proposed scheme is
entirely different scheme which will not use any aux-
iliary array information in embedding and extraction.
The earlier scheme is purely blind scheme. Where as
to achieve high embedding capacity the current pro-
posed scheme use an auxiliary array known as the
stego-key. Thus, the secret message is encoded in
both auxiliary array and stegoimage. Using stego-key
we can able to achieve an embedding capacity of 2.5
bpp. Thus, compared to T. Sharp scheme, proposed
scheme achieved150 % increase in the embeddingca-
pacity and compared to Chin-Feng scheme proposed
scheme achieves 233 % increase in embedding capac-
ity with high perceptible stegoimages. Table 3 shows
the comparisons of embedding capacity of proposed
scheme with references.
5 EFFECT OF IMAGE
PROCESSING ATTACKS
Secret image communication over insecure channel
may lead to intentional or unintentional tampering of
steganoimages. The alterations of steganoimage con-
tent is considered to be the attack on steganoimages.
SECRYPT2012-InternationalConferenceonSecurityandCryptography
20

Table 2: The NC and SC between the extracted and original secret images.
Properties Lena Baboon Peppers Chessboard
NC 1.00 1.00 1.00 1.00
SC 1.00 1.00 1.00 1.00
Table 3: Comparison of proposed scheme with Chin-Feng scheme (Lee et al., 2009) and our earlier scheme (Na-
garaj V.Dharwadkar, 2010) in terms of embedding capacity (bpp).
Lena Peppers Baboon Chessboard Security
/Barbara
Proposed 2.5 2.5 2.5 2.5 Dual stegoimages
scheme & stegokey
Our earlier scheme 1 1.12 1.1 1.20 Dual stegoimages
Chin-Feng 0.75 0.75 0.749 0.749 Dual stegoimages
scheme
(a) Gaussian
Noise density 30%
on stegoimage1.
(b) Gaussian
Noise density 30%
on stegoimage2.
(c) Gaussian filter
with 30 %stegoim-
age1.
(d) Gaussian filter
with 30 % on ste-
goimage2.
(e) Gaussian Blurr
radius of 30 pixels
on stegoimage1.
(f) Gaussian Blurr
radius of 30 pixels
on stegoimage2.
(g) Radial Blurr
radius of 30 pixels
on stegoimage1.
(h) Radial Blurr
radius of 30 pixels
on stegoimage2.
Figure 10: Effect of image processing attacks on Lena image.
In this section, we discuss the reasons for hostile and
coincidental attack on a steganoimage. The hostile
attack is an attempt to weaken, remove or alter the
hidden image. Where as the coincidental attack can
occur during common image processing and commu-
nication process. These attacks are not aimed at tam-
pering the secret image. In hostile or malicious attack,
the goal is to distort or add noise to the steganoim-
age in order to render the secret image unreadable (W
et al., 1996). The attack is successful if the secret im-
age cannot be extracted anymore. In coincidental at-
tacks, while transmission of image via Internet the im-
age is noise is added and filtered which leads to fail-
ure in the extraction of secret image. We discuss the
effect of attacks on steganoimages. For experimen-
tal analysis we have considered the image processing
attacks like filtration, adding noise and blurring. Fig-
ure 10 shows the effect of filtration, adding noise and
blurring attacks on Lena image. Figure 11 shows the
extracted secret image from attacked Lena stegoim-
age with the NC between the extracted and original
secret image.
5.1 Effect of Gaussian Filter
The effect of filtering attacks on steganoimage is an-
alyzed by applying Gaussian filter on steganoimage.
The two dimensional Gaussian filter is applied on
both stegoimage with standard deviation sigma (posi-
tive) varied from 10 to 100 %. The effect of Gaussian
filter is analyzed by calculating NC between extracted
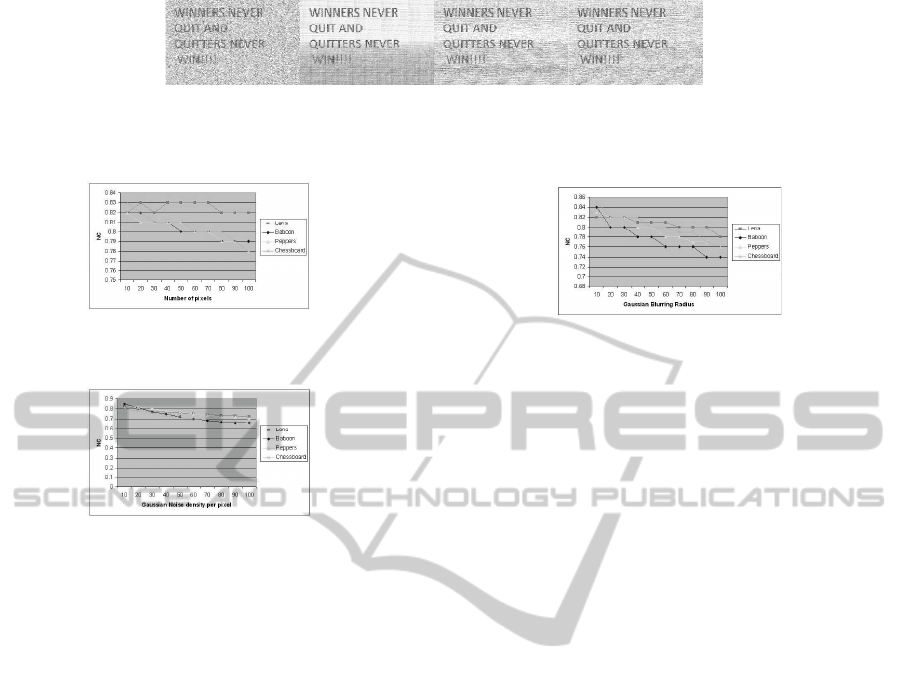
and original secret image. Figure 12 shows the effect
of Gaussian filter on extraction algorithm. The results
show that the extraction of secret image from all im-
ages produce NC between extracted and secret orig-
inal images in the range of 0.8 to 0.7 for Gaussian
filtered stegoimage with 100 % standard deviation.
From the results it was found that as the filtration fac-
tor increases, the normalized correlation between ex-
tracted and original secret image decreases. To design
a robust steganography scheme against known group
of filters, the secret image should be hidden into high
energy components of the cover image for which fil-
ters change the least.
ReversibleSteganographicSchemewithHighEmbeddingCapacityusingDualCoverImages
21
(a) Gaussian Noise
with NC= 0.68.
(b) Gaussian filter with
NC= 0.70.
(c) Gaussian Blurr with
NC=0.68.
(d) Radial Blurr with
NC= 0.70.
Figure 11: Extracted secret image from attacked Lena image.
(a) NC.
Figure 12: Effect of Gaussian filters on steganoimages.
(a) NC.
Figure 13: Effect of Gaussian noise on steganoimages.
5.2 Effect of Gaussian Noise
To analyze the effect of adding noise to stegoiamge, a
random signal with a given distribution (eg Gaussian,
uniform, Poisson, Bernoulli) is added to the image.
In certain applications the additive noise may origi-
nate from Digital-to Analog (D/A) and A/D convert-
ers, or as a consequence of transmission errors. How-
ever, an attacker may introduce perceptually shaped
noise (image-dependent mask) with maximum unno-
ticeable power. This will typically force the increase
of threshold at which the correlation of the detector
operates. The Gaussian noise is added to the stegoim-
ages with noise density d which affects approximately
d×(size(I)) pixels. The performance of extraction al-
gorithm is analyzed by increasing noise density start-
ing from 10 up to 100 pixels. The quality of ex-
tracted secret image is measured in terms of NC be-
tween original and extracted secret image. Figure 13
shows the effect of adding noise on both Stegoimage
by varying the noise density from 10 to 100 pixels.
In this experiment it is found that extraction of se-
cret image from stegoimages produces NC between
the extracted and the secret image is nearly equal to
0.80. These results show that the proposed scheme is
robust against the addition of noise.
(a) NC.
Figure 14: Effect of Gaussian blurring on steganoimages.
5.3 Effect of Gaussian Blurring
To analyze the effect of blurring on stegoiamges, a
Gaussian blurring is applied with varying blurring ra-
dius from 10 to 100 pixels. The disk radius is varied
from 10 to 100 pixels. The effect of blurring on ex-
traction algorithm is analyzed by calculating NC be-
tween secret image and extracted secret image. Figure
14 shows the effect of blurring on stegoimage in terms
of NC between secret image and extracted secret im-
age. Experimental results shows that extraction algo-
rithm produces an image which is highly correlated to
the secret image.
5.4 Effect of Radial Blurring
A Special type of circular averaging filter (pillbox fil-
ter) is applied on the both stegoimage to analyze the
effect of blurring. This filter filters the stegoimage
within the square matrix of size 2×(DiskRadius)+1.
The disk radius is varied from 10 to 100 pixels. The
effect of blurring on extraction algorithm is analyzed
by calculating NC between secret image and extracted
secret image. Figure 15 shows the effect of blurring
on stegoimage in terms of NC between secret im-
age and extracted secret image. Experimental results
shows that even at DiskRadius = 100 pixels the ex-
traction algorithm produces an image which is highly
correlated to the secret image. Thus, the proposed
scheme is robust against the blurring attack.
6 CONCLUSIONS
We have proposed a reversible dual coverimage based
steganographic scheme. The proposed scheme produ-
SECRYPT2012-InternationalConferenceonSecurityandCryptography
22

Algorithm 3: Extraction Algorithm.
input : Dual stegoimages, I
′
1
= {q
1
1
,q
1
2
,...,q
1
m×n
}
and I
′
2
= {q
2
1
,q
2
2
,...,q
2
m×n
} such that I
′
1
6= I
′
2
and stego-key of size (4× h× w)/5, where
C = {C
0
,C
1
,...,C
(4×h×w)/5
},
C
o
= {c
3
,c
2
,c
1
,c
0
} and c
k
∈ {0,1}
output: Secret image S of size h× w where
S = {s
1
,s
2
,...,s
h×w)
} and two identical
grayscale images I
1
and I
2
of size m× n
1. Set i=1; l=0; k=1; x = h× w ;
2. if (numbe of bits(stego− key) < 4) then
goto step 7.
3. if (i%2 == 1) then Embedd pexel = p
1
i
and
Ref pixel = p
2
i
else Embedd pexel = p
2
i
and
Ref pixel = p
1
i
4. select two pixels Ref pixel and Embedd pexel
and four bits of key {c
k
,c
k+1
,c
k+2
,c
k+3
}.
Switch(c
k
,c
k+1
,c
k+2
)
Case(0,0,0) : count = 0;break;
Case(0,0,1) : count = 1;break;
Case(0,1,0) : count = 2;break;
Case(0,1,1) : count = 3;break;
Case(1,0,0) : count = 4;break;
Case(1,0,1) : count = 5;break;
Case(1,1,0) : count = 6;break;
Case(1,1,1) : count = 7;break;
if (c
k+3
== 1) then p
1
i
= p
1
i
+ 4× count. else
p
1
i
= p
1
i
− 4× count
5. Select Ref pixel = (b
1
7
,b
1
6
,...,b0
1
) and
Embedd pexel = (b
2
7
,b
2
6
,...,b0
2
) respectively and
apply the following operations.
6. for j ← 0 to 4 do
Switch(b
1
j
,b
2
j
) Case(0,0) : s
j
= 1;break;
Case(0,1) : s
j
= 0;break;
Case(1,0) : s
j
= 1;break;
Case(1,1) : s
j
= 0;break;
Thus, the extracted secret bits are
(s
j−4
,s
j−3
,s
j−2
,s
j−1
,s
j
) x = x− 5.
7. set i = i+ 1;k = k+ 4;
Repeat step 3 to step 6 until x < 4.
8. if (x == 1) then if (c
k
== 0) then p = 0;
goto step 12 if (x == 2)&(c
k
== 1) then p = 0;
goto step 12
if (x == 3) then p = 1 goto step 9 else p = 2
ces perceptual good quality stegoimages with an em-
bedding capacity of 2.5 bpp. The usage of dual ste-
gaoimages and stego-key enhances the security of the
secret image. Without complete knowledge of both
stegoimages and stego-key it is difficult to determine
the secret image. From the experimental results it was
found that proposed scheme preserves the perceptual
quality of stegoimages. The proposed scheme has the
advantage of higher embedding capacity and good
Algorithm 4: Extraction Algorithm continued.
9 Select two pixels p
1
i
and p
2
i
and bits of stegokey
(c
k
,c
k+1
,c
k+2
). l = c
k+2
; Switch(c
k
,c
k+1
)
Case(0,0) : count = 0;break;
Case(0,1) : count = 1;break;
Case(1,0) : count = 2;break;
Case(1,1) : count = 3;break;
10 select two pixels p
1
i
and p
2
i
and stegokey bits
(c
k
,c
k+1
) if (c
k
== 1) then count = 1;l = c
k+1
else count = 0;
if (l == 1) then p
2
i
= p
2
i
+ 4× count else
p
2
i
= p
2
i
− 4× count
11 Select p
1
i
= (b
1
7
,b
1
6
,...,b
1
0
) and p
2
i
= (b
2
7
,b
2
6
,...,b
2
0
)
apply the following operations.
for j ← 0 to p do
Switch(b
1
j
,b
2
j
) Case(0,0) : s
j
= 1;break;
Case(0,1) : s
j
= 0;break;
Case(1,0) : s
j
= 1;break;
Case(1,1) : s
j
= 0;break;
The secret bits {s
0
,s
1
,...,s
p
} are extracted.
12 set i=1;
13 if (i%2 == 1) then p
1
i
= p
2
i
; else p
2
i
= p
1
i
;
14 i = i+ 1; Repeat step 12 to step 13
until i == m× n
aaa
(a) NC.
Figure 15: Effect of radial blurring on steganoimages.
visual quality of stegoimages. The performance of
the steganography scheme is analyzed by consider-
ing various types of image processing attacks and the
scheme was found robust to various types of image
processing attacks.
REFERENCES
Alwan, R. H., Kadhim, F. J., and Al-Taani, A. T. (2006).
Data embedding based on better use of bits in im-
age pixels. International journal of Signal Processing,
2(2):104–107.
Artz., D. (2001). Digital steganographic: Hiding data
within data. IEEE Journal on Internet Computing,
5(3):75–80.
Artz, D. (2001). Digital steganography: Hiding data within
data. IEEE Internet Computing, 5(3):75–80.
Chan, C. K. and Chen, L. M. (2004). Hiding data in images
ReversibleSteganographicSchemewithHighEmbeddingCapacityusingDualCoverImages
23

by simple lsb substitution. Elsevier Pattern Recogni-
tion, 37(3):469–474.
Chan, C. K. and Cheng, L. M. (2004). Hiding data in images
by simple lsb substitution. Elsevier Pattern Recogni-
tion, 37(3):469–474.
Cox, I., Miller, M., Bloom, J. A., Fridrich, J., and Kalker,
T. (2008). Digital Watermarking and Steganography.
Morgan Kaufmann Publishers, USA, second edition
edition.
Fridrich, J., Goljan, M., and Du, R. (2002). Lossless
data embedding new paradigm in digital watermark-
ing. EURASIP Journal on Advances in Signal Pro-
cessing, 2002(2):185–196.
Honsinger, C. W., Jones, P. W., Rabbani, M., and Stoffel,
J. C. (2001). Lossless recovery of an original image
containing embedded data.
Kahn, D. (1967). The Codebreakers The story of secret writ-
ing. Scribner, New York.
Katzenbesser, S. and Petitcolas, F. (2004). Information Hid-
ing Techniques for Steganography and Watermarking.
Artech House, Inc.Norwood, MA, USA.
Ker, A. (2005). Steganalysis of lsb matching in grayscale
images. IEEE Signal Processing Letters, 12(6):441–
444.
Lee, C.-F., Wang, K.-H., Chang, C.-C., and Huang, Y.-L.
(2009). A reversible data hiding scheme based on dual
steganographic images. In ACM proceedings of Inter-
national Conference On Ubiquitous Information Man-
agement And Communication (ICUIMC-09),Suwon,
Korea, pages 228–237.
Lee, Y. K. and Chen, L. H. (2000a). High capacity image
steganographic model. In IEE Proceedings Vision, Im-
age and Signal Processing, volume 147, pages 288–
294.
Lee, Y. K. and Chen, L. H. (2000b). High capacity im-
age steganography model. In IEEE Proceedings of Vi-
sion,Image and Signal Processing, volume 147, pages
288–294.
Mielikainen, J. (2006). Lsb matching revisited. IEEESignal
Processing Letters, 13(5):285–287.
Nagaraj V. Dharwadkar, B. B. A. (2010). Steganographic
scheme for gray-level image using pixel neighborhood
and lsb substitution. 10(4):589–607.
Nagaraj V.Dharwadkar, B. B. A. (2010). An improved re-
versible steganography scheme based on dual cover
images. International Journal of Multimedia Intelli-
gence and Security, 1(4):336–349.
Sharp, T. (2001). An implementation of key-based digital
signal steganography. In IEEE Proceedings of Infor-
mation Hiding Workshop, volume 2137, pages 13–26.
Springer LNCS.
Thien, C. C. and Lin, J. C. (2003). A simple and high-
hiding capacity method for hiding digit-by-digit data
in images based on modulus function. Elsevier Pattern
Recognition, 36(12):2875–2881.
Tian (2003). Reversible data embedding using a difference
expansion. IEEE Transactions on Circuits and Sys-
tems for Video Technology, 13(8):890–893.
W, B., D, G., N, M., and A, L. (1996). Techniques for data
hiding. 35(3-4):313–336.
Wang, R. Z., Lin, C. F., and Lin, J. C. (2001). Image hid-
ing by optimal lsb substitution and genetic algorithm.
Elsevier Pattern Recognition, 34(3):671–683.
Zou, D., Wu, C. W., Xuan, G., and Shi, Y. Q. (2003). A
content based image authentication system with loss-
less data hiding. In Proceedings of Multimedia Expo
International Conference, volume 2, pages 213–216.
IEEE.
SECRYPT2012-InternationalConferenceonSecurityandCryptography
24
