On Specification Informatics in Discrete-event Systems
State-transparency for Clarity of Finite Automata as Control Specifications
Amrith Dhananjayan and Kiam Tian Seow
School of Computer Engineering, Nanyang Technological University, 639798, Singapore, Singapore
Keywords:
Discrete-event Systems, Supervisory Control, Finite Automata, Specification Informatics, State Transparency,
Human Perception.
Abstract:
In control of discrete-event systems (DES’s), the formalization of control requirements from natural language
statements is essentially a human endeavor. Without automated support tools, human designers often face
the uncertainty of not knowing if the control requirements formalized in the rudimentary DES formalism of
automata are as intended, motivating the automata-theoretic study of specification informatics in the field of
DES’s. A specification automaton that renders its linguistic description more transparent should help design-
ers ascertain the prescribed requirement. Such transparency may be formalized in either the state space or
the event space of the DES. In this paper, treating the former as fundamental, a state-transparent specification
automaton is conceptualized with respect to a full specification automaton (‘full’ in the sense of having all
the a priori transitional constraints of the DES embedded in it). It contains only specification relevant states
called specification epochs. Each epoch denotes a “well-defined” disjoint subset of states of the full specifica-
tion automaton in the same phase of execution, meaningfully aggregated such that the resultant specification
automaton retains the original restrictiveness on the DES. The problem of maximizing the state-transparency
of specification automata for DES’s is then theoretically formulated. Subject to human perceptive or cognition
limits, we believe that such a maximally state-transparent specification automaton could be more compre-
hensible, showing clearly the compliant execution of the system through a minimum number of specification
epochs, and should aid designers in clarifying if the requirement prescribed is the one intended.
1 INTRODUCTION
Many man-made systems can be modeled as discrete-
event systems (DES’s). Supervisory control theory
for DES’s (Ramadge and Wonham, 1987) provides
a theoretical framework for synthesizing controllers
(called supervisors) for DES’s. A DES is modeled as
a finite automaton, with its possible executions gener-
ating a formal language over a finite event set. A su-
pervisor, also modeled as a finite automaton, restricts
the DES to certain sequences of events or states such
that a given set of control specifications is conjunc-
tively satisfied.
In practice, control requirements are first given
in natural language statements. In our opinion, the
potential benefits of supervisory control theory could
be better harnessed provided the specifications in au-
tomata correctly formalize these verbal or textual
statements (Ou and Hu, 2000). The translation from a
natural language statement of a control requirement
to a specification in automata is often a non-trivial
task requiring the working knowledge of the entire
DES (Cassandras and Lafortune, 2008). Often, de-
signers understand the control requirements in natu-
ral language and manually prescribe the correspond-
ing specification automata. The lack of formal tools
to help designers in turn interpret and comprehend
the specifications prescribed has been identified as a
factor limiting the effective use of supervisory con-
trol theory (Grigorov et al., 2011). Without auto-
mated support tools, designers are generally faced
with the uncertainty of whether a prescribed speci-
fication is as intended. This has been encountered in
many applications of the automata-based DES frame-
work (Grigorov et al., 2010) – in automated manu-
facturing (Magnusson et al., 2011; Cheriaux et al.,
2010), robotics (Koˇseck´a and Bajcsy, 1994; Ricker
et al., 1996), communicating transaction processes
(Feng et al., 2007), information systems (Hinze et al.,
2006) and intelligent service transportation (Seow and
Pasquier, 2004), to name a few. In fact, with advances
in computing technologies mitigating complexity to a
practically feasible extent, human comprehensibility
is turning out to be more challenging than computa-
357
Dhananjayan A. and Seow K..
On Specification Informatics in Discrete-event Systems - State-transparency for Clarity of Finite Automata as Control Specifications.
DOI: 10.5220/0003977403570367
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 357-367
ISBN: 978-989-8565-21-1
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

tional issues in solving industrial problems using su-
pervisory control theory (Wonham, 2003). This moti-
vates the automata-theoretic study of specification in-
formatics in the field of DES’s.
Psychological studies have shown that human be-
ings tend to first abstract the representation of a prob-
lem when addressing complex real world problems
(Rasmussen, 1986). In studying a problem, an on-the-
fly model abstraction of the problem could often help
a human’s limited mental capacity better understand
the essence of the problem (Bredereke and Lanke-
nau, 2005). From this empirical study, we infer that it
might be useful to have an algorithm that can abstract
an input specification automaton, and present human
designers with an output automaton that is structurally
clearer and thus easier to comprehend, but retains the
essential expressions of the requirement prescribed by
the original automaton. Such clarity or transparency
comes from accentuating specification epochal infor-
mation, and correctly suppressing information irrele-
vant to the specification without oversimplifying that
could lead to ambiguity. The development of a sys-
tematic approach to obtain such transparent specifi-
cation automata is the aim of this paper. Not unlike
any study involving human cognition, the proposed
approach is assistive and provides a necessity basis to
individual designers for understanding specification
automata.
Research on specification transparency for DES’s
originates with the work of (Pham et al., 2010).
Therein, the specification transparency maximization
problem introduced attempts to highlight the prece-
dence ordering among a minimal set of events deemed
relevant to the specification, by ‘hiding’ in self-loops
all the events that are considered irrelevant to the
specification but can occur in the DES. For many ap-
plications, it might be more desirable to specify for
the DES in terms of state sequences or trajectories
(Du and Wang, 1988; Ou and Hu, 2000; Faraut et al.,
2011). In fact, it has been noted that while design-
ers of communicationsystems would prefer to specify
restrictions on event sequences generated by a DES
model, designers of manufacturing systems would
prefer to specify restrictions as constraints on state
trajectories traced by the DES (Cao and Ho, 1990).
A specification automaton in conjunction with a DES
can equivalently be viewed as prescribing a set of
‘legal’ state trajectories of the DES. A specification
automaton that traces state trajectories suitably pro-
jected from this legal set might thus furnish a clearer
state-linguistic description that aids in easier interpre-
tation of the prescribed control requirement. This mo-
tivates an alternative but complementary formulation
of the specification transparency maximization prob-
lem studied in (Pham et al., 2010), namely, one that is
based on states rather than events.
In our theoretical development, we first introduce
the concept of state-transparency of control spec-
ifications prescribed in finite automata. A state-
transparent specification automaton is an abstraction
of a full specification automaton (‘full’ in the sense
of having all the a priori transitional constraints of the
DES embedded in it), with each of its states represent-
ing a unique epoch (or execution phase) of the DES
that is relevant to the specification. As will be formal-
ized and explained, each relevant epoch distills a dis-
joint subset of states of the full specification automa-
ton that is intraconnected. By such intraconnectivity,
any pair of states in each disjoint subset is “graphi-
cally connected” by the automaton via only the states
in the subset, such that the member states reached
by an automaton transition from the same nonmem-
ber state are all temporally strung by a DES string of
events transiting through only the states in the subset.
It is postulated that specification epochs defined and
constructed this way would have well-defined mean-
ings for a state-transparent specification automaton.
For an intuitive understanding, the reader might want
to skip ahead to Section 5 for an example of abstract-
ing the states of a full specification automaton [Fig.
4(a)] into specification epochs, and yielding a state-
transparent specification automaton [Fig. 4(b)].
Different state-transparent specification automata
resulting from a full specification automaton can rep-
resent the control requirement using different sets of
specification epochs; and any specification automaton
is said to be the most (or maximally) state-transparent
if it can retain the original restrictiveness of the speci-
fication on the DES using the least number of specifi-
cation epochs. Subject to human perceptive or cogni-
tion limits, we believe that such a maximally state-
transparent specification automaton could be more
human comprehensible. Constructing such an au-
tomaton is a state-transparency maximization prob-
lem. In this paper, we formalize this problem, which
is shown to be NP-hard elsewhere. As a polynomial
time algorithm cannot be expected for this problem,
we propose an algorithm that can run in polynomial
time and achieve maximal state-transparency in indi-
vidual cases but not in general.
The rest of this paper is organized as follows. Sec-
tion 2 reviews relevant concepts in languages and
automata theory, and in some graph basics. The
new concept of state-transparency is defined, and the
problem and NP-hardness of finding a maximally
state-transparentspecification automaton are formally
stated in Section 3. A polynomial time algorithm that
can compute state-transparent specification automata
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
358

is proposed in Section 4. An illustrative example is
presented in Section 5 to demonstrate the concept of
a state-transparent specification automaton. Section 6
presents some related work. Section 7 concludes the
paper.
2 PRELIMINARIES
2.1 Formal Languages and Automata
We follow the framework of Ramadge and Wonham
(Ramadge and Wonham, 1987). Let Σ be a finite set
of events. A string denotes a finite sequence of events
from Σ. Let Σ
∗
be the set of all finite strings from Σ
including the empty string ε. A string t
′
is a prefix of
t, if there exists a string s such that t
′
s = t.
A language L over Σ is a subset of Σ
∗
. We say L
1
is a sublanguage of L
2
if L
1
⊆ L
2
. For a language L,
its prefix closure
¯
L is the language consisting of all
prefixes of its strings. As any string s in Σ
∗
is a prefix
of itself, we have L ⊆
¯
L. A language L is considered
prefixed-closed if L =
¯
L.
Any regular language can be generated by
an automaton. An automaton G is a 5-tuple
(Q,Σ,δ, q
0
,Q
m
), where Q is the finite set of discrete
states, Σ is the finite set of discrete events, δ : Σ×Q →
Q is the (partial) transition function, q
0
is the initial
state and Q
m
⊆ Q is the set of marker states.
Write δ(σ,q)! to mean that δ(σ,q) is defined and
¬δ(σ,q)! to mean otherwise. The definition of δ can
be extended to Σ
∗
× Q in the usual way as follows.
δ(ε,q) = q,
(∀σ ∈ Σ)(∀s ∈ (Σ)
∗
)δ(sσ,q) = δ(σ,δ(s,q)).
The prefix-closed language L(G) and the marked
language L
m
(G) describe the behavior of automaton
G. Formally,
L(G) = {s ∈ Σ
∗
| δ(s,q
0
)!},
L
m
(G) = {s ∈ L(G) | δ(s,q
0
) ∈ Q
m
}.
A state q ∈ Q is reachable if (∃s ∈ Σ
∗
) δ(s,q
0
) = q,
and coreachable if (∃s ∈ Σ
∗
) δ(s,q) ∈ Q
m
. Automa-
ton G is reachable if all its states are reachable, and
is coreachable if all its states are coreachable, i.e.,
L
m
(G) = L(G). If G is both reachable and coreach-
able then it is said to be trim.
2.2 Graph Basics
Following (Diestel, 2006), an undirected graph J is
a 2-tuple (V
J
,E
J
), where V
J
is the set of nodes and
E
J
⊆ V
J
× V
J
is the set of edges. A path from node
u ∈ V
J
to node v ∈ V
J
in J is a sequence of edges in
E
J
, starting at node u and ending at node v:
(u,u
1
),(u
1
,u
2
)...(u
k−1
,u
k
)(u
k
,v).
Two nodes u and v are said to be connected if such
a path exists. A graph is connected if every pair of
nodes in V
J
is connected.
Finally, let |P| denote the cardinality of the set P.
3 PROBLEM CONCEPTS AND
DESCRIPTION
3.1 Specification Automaton and
State-transparency
Definition 1. (Pham et al., 2010) Given a DES G =
(Q,Σ,δ, q
0
,Q
m
), and a regular language L such that
L = L
m
(A), where automaton A = (X,F, ξ,x
0
,X
m
). If
A is said to be a specification automaton (of L for DES
G), then 1) F = Σ, 2) L
m
(A) ∩ L
m
(G) = L(A) ∩ L(G),
and 3) A is trim.
Intuitively, a specification automaton for DES G
models a (marked) sublanguage of G over event set
Σ. The sublanguage L
m
(A) ∩ L
m
(G) is well modeled
such that every common prefix string in L(A) ∩ L(G)
can be extended to a marked string in L
m
(A)∩ L
m
(G),
thereby specifying an uninhibited sequence of execu-
tions to complete some task.
Given a specification automaton A for G, a trim
automaton H such that L
m
(H) = L
m
(A) ∩ L
m
(G) is
said to be a full automaton, in that it embodies the
a priori transitional constraints of G, and thus repre-
sents the full nonblocking behavioral specification for
G under A. By Definition 1, H can be called a speci-
fication automaton.
Given a full specification automaton H =
(Y,Σ,ζ,y
0
,Y
m
) for DES G = (Q,Σ,δ, q
0
,Q
m
), we de-
fine the following (cf. (Su and Wonham, 2004)).
Let E :Y → 2
Σ
be the set of events defined at y ∈Y
such that E(y) = {σ ∈ Σ | ζ(σ,y)!}.
Let D : Y → 2
Σ
be the set of events not permitted
by the specification at y ∈ Y such that D(y) = {σ ∈ Σ |
¬ζ(σ,y)! and (∃s ∈ Σ
∗
)[ζ(s,y
0
) = y and δ(sσ,q
0
)!]}.
Let T : Y → {true, false} with T(y) =
true if (∃s ∈ Σ
∗
)[ζ(s,y
0
) = y and δ(s,q
0
) ∈ Q
m
].
T(y) is true if y is reachable by a string in the marked
language of G.
Let M :Y → {true, false} with M(y) = true if y ∈
Y
m
. M(y) is true if y is a marker state.
We say two states in a full specification automa-
ton H are specification compatible with each other if
their associated event permission and nonpermission
OnSpecificationInformaticsinDiscrete-eventSystems-State-transparencyforClarityofFiniteAutomataasControl
Specifications
359

in a DES G as well as their markings are consistent,
formally defined as follows.
Definition 2. Given a full specification automaton
H = (Y, Σ,ζ,y
0
,Y
m
) for a DES G, let C ⊆ Y × Y be
the set of pairs of specification compatible states of H
on G. Then:
For y, y
′
∈ Y, (y,y
′
) ∈ C iff
1. E(y) ∩ D(y
′
) = E(y
′
) ∩ D(y) =
/
0;
2. T(y) = T(y
′
) ⇒ M(y) = M(y
′
).
Condition 1 states that for (y,y
′
) ∈ C, an event
permitted at y should not be denied permission at
y
′
and vice versa. According to Condition 2, states
y,y
′
∈ Y of H such that (y, y
′
) ∈ C are consistently
marked true or false if both states are reachable
by some strings in the marked language of G (i.e.,
when T(y) = T(y
′
) = true), or if neither is reachable
by a string in the marked language of G (i.e., when
T(y) = T(y
′
) = false).
In what follows, a procedure called 13 is devel-
oped to check if a state pair is specification compati-
ble. Lemma 1 is immediate.
Procedure : ChkI fInC(y, y
′
).
Input: Two states y,y
′
∈ Y of H = (Y,Σ,ζ,y
0
,Y
m
);
Output: true if (y,y
′
) ∈ C; f alse, otherwise;
1 begin
2 if (E(y) ∩ D(y
′
)) ∪ (E(y
′
) ∩ D(y)) =
/
0 then
3 if T(y) = T(y
′
) then
4 if M(y) = M(y
′
) then
5 return true;
6 end
7 end
8 else
9 return true;
10 end
11 end
12 return false;
13 end
Lemma 1. Let C be the set of pairs of specification
compatible states of a full specification automaton
H = (Y,Σ,ζ,y
0
,Y
m
) for a DES G. Then for a pair of
input states y,y
′
∈ Y, Procedure 13(y,y
′
) returns true
iff (y,y
′
) ∈ C.
A cover of a setY is a family of subsets ofY whose
union is Y. Each element of a cover is called a cell. A
cover is a partition if its cells are pairwise disjoint.
We now define what is called a specification-
equivalent partition P over the state set of a full spec-
ification automaton H.
Definition 3. Let C be the set of pairs of specifica-
tion compatible states of a full specification automa-
ton H = (Y,Σ,ζ,y
0
,Y
m
) for a DES G. For an index
set X, a partition P = {Y
x
⊆ Y | x ∈ X} is said to be a
specification-equivalent partition of H if
1. (∀x ∈ X)(∀y,y
′
∈ Y
x
)(y, y
′
) ∈ C;
2. (∀x ∈ X)(∀σ ∈ Σ)(∃x
′
∈ X)[(∀y ∈ Y
x
)ζ(σ,y)! ⇒
ζ(σ,y) ∈ Y
x
′
].
For an index set X and a state y ∈ Y, we denote the
cell of P = {Y
x
⊆ Y | x ∈ X} containing y as [y], i.e.,
for y ∈ Y
x
, we have [y] = Y
x
.
Condition 1 of Definition 3 states that all pairs
of states within the same cell must be specification
compatible. Condition 2 asserts that, for two arbitrary
cells Y
x
and Y
x
′
of P, the states reachable via the same
event from states of the same cell Y
x
must all belong
to the same cell Y
x
′
.
According to Definition 3, two states y, y
′
∈ Y
are to be placed together in a cell of a specification-
equivalent partition if the state pair is specifiation
compatible and all the state pairs reachable by iden-
tical strings from y and y
′
are also specification com-
patible. Any two states y and y
′
that can be placed
within a cell as such are said to be pairable. It follows
that all state pairs reachable by identical strings from
pairable y and y
′
are also pairable. State pairability is
formally defined as follows.
Definition 4. Let C be the set of pairs of specification
compatible states of a full specification automaton
H = (Y,Σ,ζ,y
0
,Y
m
) for a DES G. Two states y,y
′
∈ Y
are said to be pairable if
1. (y,y
′
) ∈ C
2. (∀s ∈ Σ
∗
)[ζ(s,y)! and ζ(s,y
′
)! ⇒
(ζ(s,y),ζ(s,y
′
)) ∈ C]
In what follows, we present a procedure (cf.
(Su and Wonham, 2004)) called : PTran that
computes and returns an induced automaton A =
(X,Σ,ξ,x
0
,X
m
) from a given specification-equivalent
partition P = {Y
x
⊆ Y | x∈ X} defined on a full specifi-
cation automaton H = (Y,Σ, ζ,y
0
,Y
m
), such that each
state x ∈ X of A uniquely corresponds to cell Y
x
of P.
The initial state of A corresponds to the cell contain-
ing the initial state of H. A state of A is marked if the
corresponding cell contains any marked state of H. In
A, a transition of event σ ∈ Σ from a state x to a state
x
′
is defined if there is a transition of the same event
in H, from a state inY
x
to a state in Y
x
′
. The procedure
has a worst case complexity of O(|Y||Σ|).
Theorem 1. Given a full specification automaton H
for a DES G and a specification-equivalent parti-
tion P of H. Then under G, A = PTran(H, P) is a
specification automaton modeling L
m
(H) such that
L
m
(H) = L
m
(A) ∩ L
m
(G).
Remark 1. A specification-equivalent partition (of
Definition 3), though mathematically similar, is con-
ceptually different from a control congruence (Su and
Wonham, 2004). For a different purpose as will be
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
360

discussed in Section 6, the latter notion requires H
to be controllable; and we note that for a control con-
gruence P
c
defined on a controllable H, PTran(H, P
c
)
becomes a procedure that returns a nonblocking and
possibly state-reduced supervisor (Su and Wonham,
2004) realizing L
m
(H) for DES G. Exposing this tech-
nical correspondence, it is not unexpected that cer-
tain definitions in this paper have some similarity with
those in (Su and Wonham, 2004).
Procedure : PTran(H,P).
Input: A full specification automaton H = (Y,Σ,ζ,y
0
,Y
m
)
and a specification-equivalent partition
P = {Y
x
⊆ Y | x ∈ X} of H;
Output: An induced specification automaton A such that
each state of A uniquely represents a cell of P;
1 begin
2 x
0
= x ∈ X such that y
0
∈ Y
x
;
3 X
m
= {x ∈ X | Y
x
∩Y
m
6=
/
0};
4 ξ : Σ× X → X(pfn) with ξ(σ,x) = x
′
for (x,x
′
∈ X) and
(σ ∈ Σ), such that (∃y ∈ Y
x
)ζ(σ,y) ∈ Y
x
′ ;
5 return A = (X,Σ,ξ, x
0
,X
m
);
6 end
Given an automaton H = (Y,Σ, ζ,y
0
,Y
m
) and a
subset Y
′
⊆ Y of states, an undirected graph de-
noted by I(H,Y
′
) can be induced such that I(H,Y
′
) =
(Y
′
,E
′
) with E
′
= {(y,y
′
) | (y,y
′
∈ Y
′
) and (∃σ ∈
Σ)[ζ(σ,y) = y
′
]}.
For a partition P of the state set Y of H, we say
a cell p ∈ P is intraconnected if the states it contains
are all “graphically connected” in the automaton via
only the states within the cell, i.e., the induced graph
I(H, p) is connected.
For any given input cell p ∈ P, Procedure
CheckI fConnected conducts a breadth-first search on
the graph I(H, p) and returns true if I(H, p) is con-
nected. The procedure starts by adding a random
node of I(H, p) to a list con nodelist. The procedure
then adds to con nodelist all nodes in p that share
an edge with the selected node. This step is repeated
for each node that is added to con nodelist. Once af-
ter all nodes in con nodelist are considered and there
are no further nodes to be added to con nodelist, if
con nodelist equals p, then I(H, p) is connected. The
procedure has a complexity of O(|p||Σ|).
In what follows is the important definition of a
state-transparent partition over a full specification au-
tomaton.
Definition 5. Let X be an index set. Given a full spec-
ification automaton H = (Y,Σ,ζ,y
0
,Y
m
) for a DES G,
a state-transparent partition of H is a specification-
equivalent partition P = {Y
x
⊆ Y|x ∈ X} of H with
the following cell intraconnectivity property: (∀x ∈
X)[I(H,Y
x
) is connected].
Procedure : CheckI fConnected(p).
Input: A cell p of a partition on the state set of an
automaton H;
Output: true, if p is intraconnected; false, otherwise;
1 begin
2 (p,E
′
) = I(H, p);
3 Select any y
′′
∈ p;
4 Add y
′′
to a queue u;
5 con nodelist := {y
′′
};
6 while u is not empty do
7 Dequeue y from u;
8 foreach (y
1
,y
2
) ∈ E
′
such that y ∈ {y
1
,y
2
} do
9 Let y
′
= {y
1
,y
2
} − {y};
10 if y
′
/∈ con nodelist then
11 con nodelist := con nodelist ∪ {y
′
};
12 Add y
′
to u;
13 end
14 end
15 end
16 if p = con nodelist then
17 return true;
18 end
19 else
20 return false;
21 end
22 end
According to Definition 5, a state-transparent par-
tition is a specification-equivalent partition contain-
ing only intraconnected cells over a full specification
automaton. We postulate that these cells can be ab-
stracted to reveal well-defined specification-relevant
epochs, in what is defined as a state-transparent spec-
ification automaton.
Definition 6. Given a full specification automaton H
for a DES G. Let P be the set of all state-transparent
partitions on H. Then for P ∈ P , a specification au-
tomaton A = PTran(H,P) (for DES G) is said to be a
P-transparent specification automaton of H.
A P-transparent specification automaton formal-
izes a state-transparent specification. Intuitively, un-
der DES G, a P-transparent specification automaton A
is an abstract representation of a full specification H,
and each state of A is a specification epoch abstract-
ing a cell of the state-transparent partition P of H. By
Theorem 1, A possesses the same restrictiveness on G
as H.
We postulate that the most (or maximally) state-
transparent specification automaton A should express
the control requirement using the least number of
specification epochs, i.e., the state-transparent parti-
tion P should be of minimal cardinality.
3.2 Problem Statement
The problem of finding a maximally state-transparent
OnSpecificationInformaticsinDiscrete-eventSystems-State-transparencyforClarityofFiniteAutomataasControl
Specifications
361

specification automaton A for a full specification au-
tomaton H on DES G can now be formally stated.
Problem 1. Given a full specification automaton H
for a DES G. Let P be the set of all state-transparent
partitions on H. Construct a P-transparent specifi-
cation automaton A = PTran(H,P) of H such that
(∀P
′
∈ P )|P
′
| ≥ |P|.
Theorem 2. Problem 1 is NP-hard.
4 PROCEDURES AND SOLUTION
ALGORITHM
Since the state-transparency maximization problem is
NP-hard, a polynomial-time algorithm that can al-
ways return a specification automaton of maximal
state-transparency is not expected. In this section,
a polynomial-time algorithm that cannot guarantee
maximal state-transparency, but can often produce
maximal solution in individual cases is proposed.
By Theorem 1 and Definition 6, a state-
transparent partition induces a state-transparent spec-
ification automaton. A procedure to compute a state-
transparent partition is, therefore, essential for com-
puting a state-transparent specification automaton.
Such a procedure, : GetSTPartition, is presented in
Section 4.3. The procedure utilizes another procedure
(Section 4.1) to check for state pairability and yet an-
other procedure (Section 4.2) for checking the cell in-
traconnectivity property. In Section 4.4, a solution
algorithm for Problem 1 is then presented.
4.1 Checking of State Pairability
For two states y, y
′
∈ Y of a full specification automa-
ton H = (Y,Σ,ζ, y
0
,Y
m
), Procedure : ChkI fPairable
checks if the input states y and y
′
are pairable. For
this, initially, the procedure checks if the input state
pair is specification compatible (Condition 1 of Defi-
nition 4) by invoking Procedure 13 and thereafter re-
cursively checks if all state pairs reachable by iden-
tical strings from the input state pair are also specifi-
cation compatible (Condition 2 of Definition 4). The
procedure returns true if all the state pairs considered
are specification compatible; and false, otherwise. A
list waitlist (that is initialized to the empty set
/
0 when-
ever Procedure : ChkI fPairable is invoked by Proce-
dure : GetSTPartition) is updated with each state pair
that is considered. The procedure has a complexity of
O(|Y|
2
)
Procedure : ChkI fPairable(y,y
′
,waitlist).
Input: Two states y,y
′
of input specification automaton H, a
list waitlist of states pairs considered so far;
Output: true, if y and y
′
are pairable; false, otherwise;
with waitlist updated;
1 begin
2 Let W(y) = {y
′′
| {(y,y
′′
),(y
′′
,y)} ∩ waitlist 6=
/
0};
3 foreach y
1
∈ [y]∪
S
y
′
1
∈W(y)
[y
′
1
] do
4 foreach y
2
∈ [y′]∪
S
y
′
2
∈W(y′)
[y
′
2
] do
5 if {(y
1
,y
2
),(y
2
,y
1
)} ∩ waitlist =
/
0 and [y
1
] 6= [y
2
] then
6 if ChkI f InC(y
1
,y
2
) = false then
7 return false;
8 end
9 waitlist := waitlist ∪{(y
1
,y
2
)};
10 foreach
σ ∈ Σ such that ζ(σ,y
1
)! and ζ(σ,y
2
)!
do
11 flag = ChkI f Pairable(ζ(σ,y
1
),
ζ(σ,y
2
),waitlist);
12 if f lag = false then
13 return false;
14 end
15 end
16 end
17 end
18 end
19 return true;
20 end
Procedure : GetCnctPartition(waitlist,P).
Input: A list waitlist of pairable state pairs and a
state-transparent partition P;
Output: A partition P
′
that augments P such that the states
paired in waitlist are placed within same cells,
whenever P
′
has only intraconnected cells; P,
otherwise;
1 begin
2 Let W(y) = {y
′′
| {(y,y
′′
),(y
′′
,y)} ∩ waitlist 6=
/
0};
3 P
′
= {[y]∪
S
y
′
∈W(y)
[y
′
] | [y],[y
′
] ∈ P};
4 foreach p ∈ P
′
do
5 flag = CheckI fConnected(p);
6 if f lag = f alse then
7 return P;
8 end
9 end
10 return P
′
;
11 end
4.2 Checking of Cell Intraconnectivity
For a list waitlist of pairable state pairs and a state-
transparent partition P, Procedure : GetCnctPartition
augments P to a partition of states of H such that the
state pairs in waitlist are placed within same cells
of the partition. Each cell of the newly computed
partition is checked for intraconnectivity by invoking
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
362

Procedure : CheckI fConnected. If each of its cells
is intraconnected, the newly computed partition is a
state-transparent partition and is returned by Proce-
dure : GetCnctPartition. Otherwise, the input state-
transparent partition is returned without any modifi-
cation. The procedure has a complexity of O(|Y|
2
).
Procedure : GetSTPartition(H, G).
Input: A full specification automaton H = (Y,Σ,ζ,y
0
,Y
m
)
on DES G;
Output: A state-transparent partition P of H;
1 begin
2 P = {[y] | [y] = {y} for y ∈ Y};
3 foreach y ∈ Y do
4 foreach σ ∈ Σ do
5 if ζ(σ,y)! then
6 Let y
′
= ζ(σ,y);
7 waitlist :=
/
0;
8 flag = ChkI f Pairable(y,y
′
,waitlist);
9 if f lag = true then
10 P = GetCnctPartition(waitlist, P);
11 end
12 end
13 end
14 end
15 return P;
16 end
4.3 Computation of a State-transparent
Partition
For an input full specification automaton H on DES
G, Procedure : GetSTPartition computes a state-
transparent partition P of H. Initially, the proce-
dure defines P such that each state belongs to a dis-
tinct cell. Then, for each pair of states that are con-
nected in H by a transition, the procedure invokes
Procedure ChkI fPairable to check if the state pair
is pairable. Procedure : ChkI fPairable returns true
if its input state pair is pairable, with waitlist hav-
ing a list of state pairs that are reachable by iden-
tical strings from the input state pair. Whenever,
Procedure : ChkI fPairable returns true, Procedure
: GetCnctPartition is invoked. As explained in the
preceding subsection, Procedure : GetCnctPartition
updates P by placing within same cells those states
that are paired in waitlist, provided the cell intracon-
nectivity property is satisfied. Otherwise, the state-
transparent partition is not updated. The procedure
terminates after it has considered all pairs of states in
H connected by a transition. The complexity of the
procedure is O(|Y|
3
|Σ|)
4.4 Solution Algorithm
For an input full specification automaton H on DES
Algorithm 1: Computation of a state-transparent
specification automaton.
Input: A full specification automaton H on DES G;
Output: A state-transparent specification automaton A of
H;
1 begin
2 P = GetSTPartition(H,G);
3 A = PTran(H,P);
4 return A;
5 end
G, Algorithm 1 computes a state-transparent specifi-
cation automaton A of H. Procedure : GetSTPartition
computes and returns a state-transparent partition
P of H. The algorithm returns automaton A =
PTran(H,P), which by Definition 6, is a P-
transparent specification automaton of H. The com-
plexity of Algorithm 1 is O(|Y|
3
|Σ|). The complexity
of Algorithm 1 is the sum of complexities of proce-
dures : GetSTPartition and : PTran, i.e., O(|Y|
3
|Σ|+
|Y||Σ|) ≈ O(|Y|
3
|Σ|).
Theorem 3. For a full specification automaton H
on DES G, Algorithm 1 returns a state-transparent
specification automaton A of H such that L
m
(H) =
L
m
(A) ∩ L
m
(G).
I/O
X
I/O
Y
M1 M2
1load
X
1release
X
2load
X
1release
Y
2release
X
R
2load
Y
2release
Y
1load
Y
Figure 1: FMS layout.
5 ILLUSTRATIVE EXAMPLE
In this section, we illustrate the concept of state-
transparency using an example of a flexible manufac-
turing system (FMS) adapted from (Uzam, 2004). As
shown in Fig. 1, the FMS consists of two machines
M1 and M2, and a robot R, all capable of handling
parts of two different types X and Y. Parts of type
X enter and leave the FMS through an infinite-size
buffer I/O
X
and those of type Y through an infinite-
size buffer I/O
Y
. Each machine can process only one
part at a time, and the robot can hold only one part at
a time. The production cycles for part types X and Y
are as follows.
X : M1 → R → M2
Y : M2 → R → M1
In the former cycle, a part of type X is first loaded into
machine M1 for initial-stage processing, before robot
R takes and loads it into machine M2 for final-stage
processing. In the latter cycle, a part of type Y is first
OnSpecificationInformaticsinDiscrete-eventSystems-State-transparencyforClarityofFiniteAutomataasControl
Specifications
363

1load
X
m
I
1
m
X
1
m
Y
1
1release
X
1load
Y
1release
Y
(a) Machine M1
2load
X
m
I
2
m
X
2
m
Y
2
2release
X
2load
Y
2release
Y
(b) Machine M2
2release
Y
r
I
r
Y
r
X
1load
Y
1release
X
2load
X
(c) Robot R
Figure 2: FMS models.
loaded into machine M2 for initial-stage processing,
before robot R takes and loads into machine M1 for
final-stage processing.
As depicted in Figs. 2(a) and 2(b), machines M1
and M2 transit among states idling (m
1
I
, m
2
I
), process-
ing X (m
1
X
, m
2
X
) and processing Y (m
1
Y
, m
2
Y
), respec-
tively. The robot R transits among states idling (r
I
),
holding X (r
X
) and holding Y (r
Y
), as depicted in Fig.
2(c). Note that in the directed graph representation
of an automaton, a state is represented by a node,
and a state-to-state transition by a directed edge la-
beled with an event. The initial state is represented
by a node with an entering arrow, and a marker state
by a node drawn as a double-concentric circle. For
i ∈ {1, 2}, event iload
X
represents the loading of X
into Mi for processing and event irelease
X
represents
the release of X by Mi after processing. Similarly,
event iload
Y
represents the loading of Y into Mi and
event irelease
Y
represents the release of Y by Mi.
The DES G for the FMS is formed by the syn-
chronous product (Cassandras and Lafortune, 2008)
of M1, M2 and R. A control requirement for G is
that, once the processing of a part of type X starts,
the processing of a part of type Y cannot start un-
til the processing of the part of type X is completed,
and vice versa. The full specification automaton H
of this requirement for G is shown in both Figs. 3(a)
and 4(a). It is derived from some specification au-
tomaton B prescribed by a system designer such that
L
m
(B) ∩ L
m
(G) = L
m
(H) ⊆ L
m
(G).
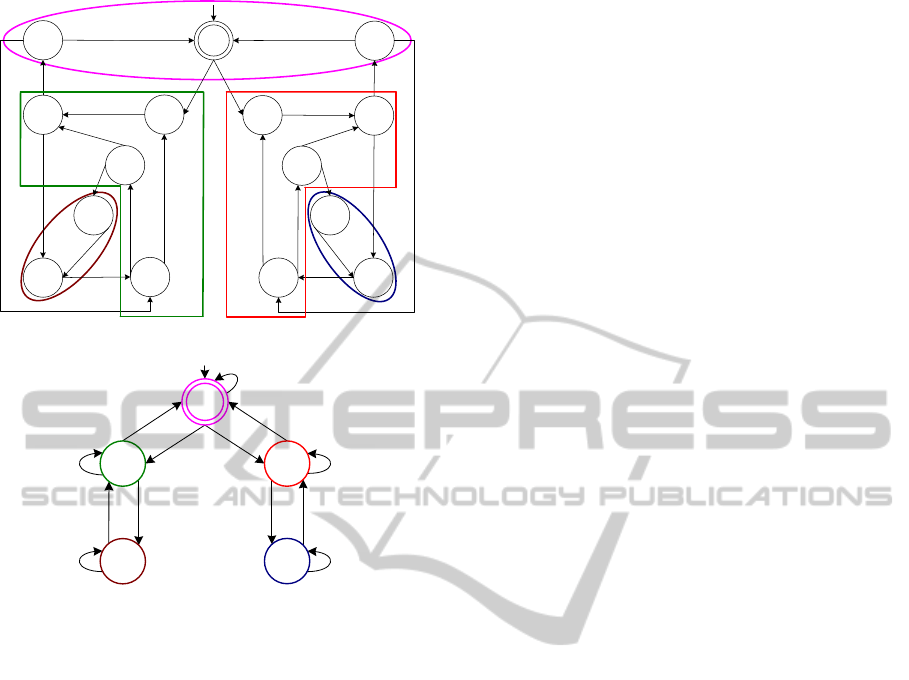
Fig. 3 shows a specification-equivalent partition
of minimal cardinality [Fig. 3(a)] over H that induces
a minimal-state specification automaton MIN [Fig.
3(b)] of H. It has been pointed out in (Wonham, 2003)
that the control requirement prescribed in MIN is
not easy to comprehend. The specification-equivalent
partition in Fig. 3(a) used to construct MIN is not a
state-transparent partition. Notice that the cell that in-
duces state 1 of MIN does not satisfy the cell intracon-
nectivity property; intuitively, it means the cell con-
tains states in clearly different phases of execution,
such as m
1
X
r
I
m
2
I
that occurs when a part of type X is
processed, and m
1
I
r
I
m
2
Y
that occurs when a part of type
Y is processed. Due to this, both the events 1load
X
m
X
1
r
I
m
I
2
m
I
1
r
I
m
Y
2
m
I
1
r
X
m
I
2
m
I
1
r
I
m
X
2
m
X
1
r
X
m
I
2
m
X
1
r
I
m
X
2
m
I
1
r
X
m
X
2
m
X
1
r
X
m
X
2
m
I
1
r
Y
m
I
2
m
Y
1
r
I
m
I
2
m
Y
1
r
I
m
Y
2
m
I
1
r
Y
m
Y
2
m
Y
1
r
Y
m
I
2
m
Y
1
r
Y
m
Y
2
2 r e l e a s e
X
1load
X
2load
Y
2release
Y
1load
Y
2load
X
1release
X
1load
X
2load
X
1release
X
2release
X
1load
X
2release
X
2release
X
1release
Y
1load
Y
2load
Y
2load
Y
1release
Y
2load
Y
1load
X
m
I
1
r
I
m
I
2
1release
Y
2release
Y
1release
Y
(a) Minimal specification-equivalent partition over the full specification au-
tomaton H
0
2 1 3
1load
X
, 2load
Y
1release
X
2release
Y
2load
Y
1load
X
2load
X
1load
Y
1release
Y
2load
X
, 2release
X
,
1load
Y,
1release
Y
2release
X
2release
X
,
1release
Y
(b) The resultant minimal state specification automaton MIN
Figure 3: Specification state minimization.
and 2load
Y
, that initiate respectively the processing
of parts of type X and Y, lead to state 1 in MIN. As a
result, this state does not form a meaningful specifica-
tion epoch in MIN as it represents either “type-X part
processing” or “type-Y part processing”. This is am-
biguous, in that type-X part processing could be con-
fused with executing event 1load
X
followed by event
2release
Y
, when the latter event should be executed
only following a type-Y part processing.
Algorithm 1 returns a state-transparent specifica-
tion automaton A (which incidentally is maximal)
over H, as shown in Fig. 4(b). The state-transparent
partition computed on H is shown in Fig. 4(a). Each
state of A abstracts a cell of the computed state-
transparent partition of H. As will be explained, each
such cell has states in the same phase of execution.
Note in Fig. 4(a) that when event 1load
X
brings the
system from the initial state m
1
I
r
I
m
2
I
of H to state
m
1
X
r
I
m
2
I
, it means that the system has started process-
ing a part of type X. To help better understand speci-
fication H, in conformance with Definition 5, our al-
gorithm aggregates the state m
1
X
r
I
m
2
I
with other states
in H, forming a cell of pairable and intraconnected
states, to distill a well-defined specification epoch
meaningfully interpreted as “Processing X”. Other
specification epochs that result can also be interpreted
meaningfully. Effectively, the output state-transparent
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
364

m
X
1
r
I
m
I
2
m
I
1
r
I
m
Y
2
m
I
1
r
X
m
I
2
m
I
1
r
I
m
X
2
m
X
1
r
X
m
I
2
m
X
1
r
I
m
X
2
m
I
1
r
X
m
X
2
m
X
1
r
X
m
X
2
m
I
1
r
Y
m
I
2
m
Y
1
r
I
m
I
2
m
Y
1
r
I
m
Y
2
m
I
1
r
Y
m
Y
2
m
Y
1
r
Y
m
I
2
m
Y
1
r
Y
m
Y
2
2 r e l e a s e
X
1load
X
2load
Y
2release
Y
1load
Y
2load
X
1release
X
1load
X
2load
X
1release
X
2release
X
1load
X
2release
X
2release
X
1release
Y
1load
Y
2load
Y
2load
Y
1release
Y
2load
Y
1load
X
m
I
1
r
I
m
I
2
1release
Y
Processing X
Processing Y
Another X
Another Y
Idling
2release
Y
1release
Y
(a) Minimal state-transparent partition over the full specification automaton
H
1load
X
2load
Y
1load
Y
2load
X
1load
X
2load
Y
2load
X
1load
Y
1release
X
,
2release
X
2release
Y
,
1release
Y
2release
X
2release
X
,
1release
Y
Idling
1release
Y
Processing
Y
Processing
another Y
Processing
X
Processing
another X
(b) The resultant maximally state-transparent specification au-
tomaton A
Figure 4: Specification state-transparency maximization.
specification automaton A ‘summarizes’ state infor-
mation in H as specification epochs, highlighting only
the essential restrictions on the DES. The specifica-
tion automaton A is easier to comprehend, since the
temporal essence of the specification - that once the
processing of a part of type X starts, the processing of
a part of type Y cannot start until the processing of the
part of type X is completed, and vice versa - is clearly
depicted in A.
6 RELATED WORK
Within the DES control community, design compre-
hensibility is receivingincreasing attention and recog-
nition. Current efforts focus primarily on clarifying
supervisor design, whereas our work focuses on clar-
ifying given specifications:
• In the former line of research, state reduction of
synthesized supervisors has been proposed as a
technique that might render the control actions
due to a specification more readily comprehensi-
ble to designers (e.g., (Su and Wonham, 2004)).
Over a controllable specification automaton gen-
erating a sublanguage of the DES, the supervisor
reduction algorithm in (Su and Wonham, 2004)
constructs a control congruence,which essentially
is a partition of states of the input automaton, and
uses it to compute a state-reduced supervisor au-
tomaton. By “virtually setting” all events as con-
trollable, one could adapt the algorithm to achieve
state size reductionfor a full specification automa-
ton. In some cases a state-reduced automaton con-
structed may be easier to understand, but the out-
put of such a state reduction procedure (Su and
Wonham, 2004) is usually not appealing to human
engineers (Wonham, 2003). The reason is that
the output often also abstracts away those a pri-
ori DES constraints essential for interpreting the
specification. The fact of the matter is that the
main aim in (Su and Wonham, 2004) is to con-
struct a supervisor automaton to achieve economy
of implementation, using the least possible num-
ber of control states by removing constraints al-
ready enforced by the DES. Also related is the re-
search (Miremadi et al., 2008) that generates and
attaches propositional formulae called guards to a
given supervisor to aid in design clarity.
• In this paper, along our latter and complementary
line of research, state-transparency is introduced
and developed. Our aim is to re-express a speci-
fication automaton using the minimum number of
specification relevant states manifesting as speci-
fication epochs, so as to aid in clarifying if it spec-
ifies the intended requirement.
Finally, the concept of state-transparency provides a
different language perspective to clarifying specifica-
tions from that of event-transparency introduced in
(Pham et al., 2010). This is manifested by two main
differences as follows. First, in the case of maxi-
mal state-transparency, a specification is recast us-
ing the least possible number of specification rele-
vant states, with each state representing some unique
specification epoch. In the case of maximal event-
transparency, the precedence ordering among a mini-
mal set of events deemed relevant to the specification
is highlighted. Second, states in a state-transparent
specification automaton correspond to a state parti-
tion of a full specification, but are not so for an
event-transparentspecification automaton. The event-
transparency maximization algorithm developed in
(Pham et al., 2010) allows unrestricted state splitting,
causing in some cases, an event that is not permit-
ted and therefore undefined in a state of a given in-
put full specification automaton to be undefined at
several states of the output event-transparent automa-
ton. This could result in a cluttered state structure
OnSpecificationInformaticsinDiscrete-eventSystems-State-transparencyforClarityofFiniteAutomataasControl
Specifications
365

of the automaton. In other words, event-transparency
tends to facilitate clarity in event ordering informa-
tion, whereas state-transparency facilitates clarity in
temporal state information.
7 CONCLUSIONS
The study of informatics for the clarification of
discrete-event control specifications in automata is
motivated, and the informatics notion of state-
transparency is developed. A state-transparent speci-
fication automaton is formally defined and a solution
algorithm to construct a specification automaton of
significant state-transparency is proposed. An illus-
trative example is given to highlight how such an au-
tomaton can enhance the intuitive understanding of a
specification in automata.
To enhance specification comprehensibility, our
future work will incorporate temporal logic to ex-
tend our state-transparency specification framework
to a dual-language framework. Temporal logic is a
natural language readable and expressive formalism
for writing specifications (Manna and Pnueli, 1992).
An algorithm is proposed in (Seow, 2007) to trans-
late a state-based (finitary) temporal logic specifica-
tion for a DES G to a full specification automaton
H. An algorithm that directly translates such a tem-
poral logic specification to a state-transparent spec-
ification automaton A for which L
m
(H) = L
m
(A) ∩
L
m
(G) should be of great practical utility to design-
ers prescribing specification for DES’s. Such a dual-
language framework can give designers added confi-
dence in ascertaining whether a prescribed specifica-
tion is as intended by rendering the control require-
ment of the translated specification automaton eas-
ier to understand from the integrated perspective of
automaton state-transparency clarified with readable
temporal state information.
ACKNOWLEDGEMENTS
This research is funded by the Singapore Ministry
of Education, under NTU-AcRF Tier 1 Grant No:
RG65/07.
REFERENCES
Bredereke, J. and Lankenau, A. (2005). Safety-relevant
mode confusions–modelling and reducing them. Reli-
ability Engineering & System Safety, 88(3):229 – 245.
Cao, X.-R. and Ho, Y.-C. (1990). Models of discrete event
dynamic systems. IEEE Control Systems Magazine,
10(4):69 – 76.
Cassandras, C. G. and Lafortune, S. (2008). Introduction to
Discrete Event Systems. Springer.
Cheriaux, F., Picci, L., Provost, J., and Faure, J.-M. (2010).
Conformance test of logic controllers of critical sys-
tems from industrial specifications. In Proceedings of
the European Conference on Safety and Reliability.
Diestel, R. (2006). Graph theory. Springer.
Du, Y. and Wang, S. H. (1988). Translation of output con-
straint into event constraint in the control of discrete
event systems. In Proceedings of the IEEE Confer-
ence on Decision and Control, volume 2, pages 1119
–1124.
Faraut, G., Pi´etrac, L., and Niel, E. (2011). Process track-
ing by equivalent states in modal supervisory control.
In Proceedings of the IEEE Conference on Emerging
Technologies & Factory Automation, pages 1 – 8.
Feng, L., M.Wonham, W., and Thiagarajan (2007). Design-
ing communicating transaction processes by supervi-
sory control theory. Formal Methods in System De-
sign, 30:117–141.
Grigorov, L., Butler, B., Cury, J., and Rudie, K. (2010).
Conceptual design of discrete-event systems using
templates. Discrete Event Dynamic Systems, pages
1–47.
Grigorov, L., Butler, B., Cury, J., and Rudie, K. (2011).
Conceptual design of discrete-event systems using
templates. Discrete Event Dynamic Systems, 21:257–
303.
Hinze, A., Malik, P., and Malik, R. (2006). Interaction de-
sign for a mobile context-aware system using discrete
event modelling. In Proceedings of the Australasian
Computer Science Conference, pages 257–266.
Koˇseck´a, J. and Bajcsy, R. (1994). Discrete event sys-
tems for autonomous mobile agents. Robotics and Au-
tonomous Systems, 12(3-4):187–198.
Magnusson, P., Sundstr¨om, N., Bengtsson, K., Lennart-
son, B., Falkman, P., and Fabian, M. (2011). Plan-
ning transport sequences for flexible manufacturing
systems. In Proceedings of the IFAC World Congress.
Manna, Z. and Pnueli, A. (1992). The temporal logic of
reactive and concurrent systems. Springer-Verlag.
Miremadi, S., Akesson, K., and Lennartson, B. (2008).
Extraction and representation of a supervisor using
guards in extended finite automata. In International
Workshop on Discrete Event Systems, pages 193 –199.
Ou, Y.-C. and Hu, J. (2000). A modified method for super-
visor specification and synthesis of a class of discrete
event systems. Asian Journal of Control, 2(4):263–
273.
Pham, M. T., Dhananjayan, A., and Seow, K. T. (2010). On
the transparency of automata as discrete-event control
specifications. In Proceedings of the IEEE Interna-
tional Conference on Robotics and Automation, pages
1474–1479.
Ramadge, P. J. and Wonham, W. M. (1987). Supervisory
control of a class of discrete event processes. SIAM
Journal of Control and Optimization, 25(1):206–230.
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
366

Rasmussen, J. (1986). Information processing and human-
machine interaction: an approach to cognitive engi-
neering. North-Holland.
Ricker, S. L., Sarkar, N., and Rudie, K. (1996). A discrete
event systems approach to modeling dextrous manip-
ulation. Robotica, 14(5):515–525.
Seow, K. T. (2007). Integrating temporal logic as a state-
based specification language for discrete-event control
design in finite automata. IEEE Transactions on Au-
tomation Science and Engineering, 4(3):451–464.
Seow, K. T. and Pasquier, M. (2004). Supervising passenger
land-transport systems. IEEE Transactions on Intelli-
gent Transportation Systems, 5(3):165–176.
Su, R. and Wonham, W. M. (2004). Supervisor reduction
for discrete-event systems. Discrete Event Dynamic
Systems: Theory and Applications, 14(1):31–53.
Uzam, M. (2004). An optimal deadlock prevention pol-
icy for flexible manufacturing systems using petri
net models with resources and the theory of regions.
The International Journal of Advanced Manufactur-
ing Technology, 19(3):192–208.
Wonham, W. M. (2003). Supervisory control theory: Mod-
els and methods. In Proc. ATPN - Workshop on Dis-
crete Event Systems Control, International Confer-
ence on Application Theory of Petri Nets, pages 1–14.
OnSpecificationInformaticsinDiscrete-eventSystems-State-transparencyforClarityofFiniteAutomataasControl
Specifications
367