Differential Space Time Block Codes for High Mobility Scenarios
Benigno Rodr´ıguez
Institute of Electrical Engineering, Universidad de la Rep´ublica, Julio Herrera y Reissig 565, Montevideo, Uruguay
Keywords:
OFDM, MIMO, DSTBCs, WiMAX, LTE, Wireless Broadband Mobile Networks.
Abstract:
In this paper the advantages of using a particular class of Differential Space Time Block Codes (DSTBCs)
in high mobility scenarios are reported. This is a high bandwidth efficiency technique with specially good
performance when the mobile terminal velocity is high.
For Orthogonal Frequency Division Multiplexing (OFDM) based systems in high mobility scenarios, as the
ones that can be considered for Worldwide Interoperability for Microwave Access (WiMAX) and Long Term
Evolution (LTE), the analyzed technique reports improvements of up to 14 dB with respect to the use of 64PSK
in DSTBCs.
1 INTRODUCTION
Space diversity produces well known benefits over
the performance of wireless systems. One alternative
to achieve it, is by using Space Time Block Codes
(STBCs) (Alamouti, 1998), (Tarokh et al., 1999),
which were quite successful and very well accepted
as an interesting solution for improving the trans-
mission quality in wireless systems. More precisely
STBC is one of the three operation modes considered
in IEEE802.16e (Matrix A, Matrix B and Beamform-
ing). STBC (Matrix A operation mode) provides in
this case a robust transmission mode useful in low
SNR scenarios.
But space diversity schemes have a price, as in
all Multiple Input Multiple Output (MIMO) systems.
The price is a more complex channel estimation pro-
cess, because more channels are involved in the com-
munication. This complexity grows with the order of
the MIMO system. If we consider a MIMO system
with two transmit antennas and three receive anten-
nas (MIMO 2x3), then six channels must be estimated
and corrected in order to have an acceptable qual-
ity in the transmission. Therefore, differential coding
schemes as DSTBCs have been proposed (Tarokh and
Jafarkhani, 2000; Tao and Cheng, 2001; Xia, 2002;
Chen et al., 2003; Hwang et al., 2003; Bauch, 2004;
Bauch and Mengi, 2005), which do not need any in-
formation about the radio channel. The information
is transmitted in this case as the quotient between two
adjacent modulation symbols which are equally af-
fected by the channel. That allows the elimination
of the channel influence in the receiver and for this
reason is not necessary to cope with complex channel
estimation and correction procedures. That become
the DSTBC schemes a quite attractive technique to
increase the number of antennas in the system in order
to obtain better performance.
In (Rodr´ıguez and Rohling, 2006), (Rodr´ıguez
and Rohling, 2007) and (Rodr´ıguez, 2007) a new
class of DSTBC was proposed and exhaustively an-
alyzed. This paper discusses the system performance
of this particular class of DSTBCs for high mobility
scenarios.
2 DESCRIPTION OF AN
IMPROVED DSTBC SCHEME
In all this work a flat radio channel transfer function
is considered, which is an acceptable assumption for
each subcarrier in a multicarrier system, in particular
for OFDM systems.
As it was described in (Rodr´ıguez and Rohling,
2006), the first step is to obtain the information matrix
S
k
which contains the two complexvalued modulation
symbols s1
k
and s2
k
.
S
k
=

s1
k
s2
k
−s2
∗
k
s1
∗
k

(1)
Then the rule to obtain the differential modulation is
shown in the next equation.
C
k
= S
k
·C
k−1
=

c1
k
c2
k
−c2
∗
k
c1
∗
k

(2)
377
Rodríguez B..
Differential Space Time Block Codes for High Mobility Scenarios.
DOI: 10.5220/0003980903770381
In Proceedings of the International Conference on Signal Processing and Multimedia Applications and Wireless Information Networks and Systems
(WINSYS-2012), pages 377-381
ISBN: 978-989-8565-25-9
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

Where C
k
is the matrix to be transmitted.
In the receiver the following matrix R
k
is obtained:

r1
k
−r2
∗
k
r2
k
r1
∗
k

=

c1
k
c2
k
−c2
∗
k
c1
∗
k

·

h1
k
−h2
∗
k
h2
k
h1
∗
k

+

n1
k
−n2
∗
k
n2
k
n1
∗
k

(3)
in a summarized form
R
k
= C
k
·H
k
+ N
k
(4)
Where C
k
is the transmitted matrix, H
k
is the chan-
nel matrix and N
k
is the noise matrix -Additive
White Gaussian Noise (AWGN) mainly added in the
receiver-.
The incoherent decoding procedure is performed
as indicated in the next equation
D
k
= R
k
·R
−1
k−1
≃C
k
·H
k
·(C
k−1
·H
k−1
)
−1
= C
k
·H
k
·H
−1
k−1
·C
−1
k−1
(5)
where the noise influence was ignored.
By assuming that the channel does not vary in a
short time interval, i.e.
H
k
= H
k−1
the following result can be obtained (see (2))
D
k
≃C
k
·C
−1
k−1
= S
k
(6)
The used modulation scheme was “4A16PSK”
defined in (Rodr´ıguez and Rohling, 2006). This mod-
ulation scheme has two subconstellations, a small
and a big one. It has 4 amplitude values and 16 phase
values for each subconstellation. Each constellation
has 2 subconstellations with one amplitude value
in common (a1 =
√
0.5); 7 different amplitudes for
the whole constellation (see Fig. 1). In “4A16PSK”
modulation scheme the set of possible amplitudes
A is determined by a parameter a = 1.4 (optimum
value) as follows:
A ∈ {(
√
0.5) ·[1/a
3
,1/a
2
,1/a, 1, a,a
2
,a
3
]}
(coding [01,11, 10,00, 01,11, 10] respectively)
and the phases are 16 equal spaced phase states
starting in 0
◦
. These phases map 4 bits onto one
modulation symbol in a Gray coding way. The small
subconstellation is composed by those constellation
points with amplitude smaller or equal to a1 =
√
0.5
(“·” and “+” in Fig. 1) and the big one by those
constellation points with amplitude bigger or equal to
a1 =
√
0.5 (“+” and “∗” in the same figure).
In the transmitter a Power Control Mechanism
(PCM) decides which of both subconstellations
−2 −1.5 −1 −0.5 0 0.5 1 1.5 2
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
Figure 1: “4A16PSK” modulation scheme used in DSTBC.
should be used in order to control the transmit power.
When the small subconstellation is used the trans-
mit power is decreased or maintained. To increase or
maintain the transmit power the big subconstellation
is used.
In (Rodr´ıguez and Rohling, 2006) it was sug-
gested a PCM (PCM1) based in the observation of
the spectral norm of the previous transmit matrix
(kC
k−1
k
2
). kC
k
k
2
≡ (maximum eigenvalue (C
H
k
·
C
k
))
1/2
, where H means Hermitian. For matrices
as the C
k
matrix defined in (2) it can be written as
kC
k
k
2
= (|c1
k
|
2
+ |c2
k
|
2
)
1/2
.
This is basically the procedure, which has been
proposed in (Rodr´ıguez and Rohling, 2006). Later it
was found that better performance can be achieved,
by taking the decision of what subconstellation to
use (the small or the big one), after calculating the
kC
k
k
2
values that the use of these subconstellations -
for mapping s1
k
and s2
k
- would produce (Rodr´ıguez,
2007). This is a PCM (PCM2) based in the obser-
vation of the possible values of kC
k
k
2
, rather than in
the observation of the spectral norm of the previous
transmitted matrix (kC
k−1
k
2
).
The main difference here is that this PCM is not
any more based in C
k−1
(the previous transmitted ma-
trix) but in the possible C
k
matrices to transmit. The
objective of the PCMs is to maintain kC
k
k
2
fluctuat-
ing around a given value. In (Rodr´ıguez, 2007) and
(Jiang et al., 2010) the performance of “4A16PSK”
with PCM2 in a Rayleigh fading channel can be ob-
served and compared with 64-PSK in DSTBC.
A variation of these control power mechanisms,
based also in two subconstellations, was later consid-
ered in (Fellenberg and Rohling, 2009). In this case a
64-QAM scheme is considered and evaluated.
WINSYS2012-InternationalConferenceonWirelessInformationNetworksandSystems
378

For a comparative evaluation of “4A16PSK
PCM2” the reader can check (Xia, 2002), (Bauch,
2004), (Vanaev and Rohling, 2006), and (Fellenberg
and Rohling, 2009); there different Amplitude and
Phase Shift Keying (APSK) modulation schemes for
DSTBC are analyzed.
3 SIMULATION RESULTS
Considering typical parameters for a WiMAX system
in a Wide Sense Stationary Uncorrelated Scattering
(WSSUS) channel, the performance of “4A16PSK
PCM2” for different velocities of the mobile terminal
was evaluated and compared with the use of 64-PSK
in DSTBC.
When the simulations are performed for a single
subcarrier (f
0
), the time variance is described as fol-
lows (Hoeher, 1992)
h(τ,t) =
1
√
P
·
P
∑
p=1
δ(τ−τ
p
) ·e
j(2π f
D,p
t+θ
p
)
(7)
by making a Fourier transform of (7) in the direction
of τ and using the time as discrete (t = nT), (8) is
obtained
H( f,nT) =
1
√
P
·
P
∑
p=1
e
j2πf
D,p
nT
·e
jθ
p
·e
−j2π fτ
p
(8)
then by evaluating (8) in f = f
0
the used equation is
obtained
H( f
0
,nT) =
1
√
P
·
P
∑
p=1
e
j2πf
D,p
nT
·e
jθ
p
·e
−j2π f
0
τ
p
(9)
Where θ
p
, τ
p
and f
D,p
are obtained by using their re-
spective probability density functions.
The set of parameters used in order to perform the
simulations was inspired in a WiMAX standard and is
contained in Table 1.
For successive transmitted matrices (C
k
andC
k−1
),
successive samples of the WSSUS channel (H
k
and
H
k−1
) were used. Then it is valid H
k
≈ H
k−1
instead
of H
k
= H
k−1
(sometimes used), which is a much
more realistic assumption.
In Fig. 2 the performance of the average of
64-PSK in DSTBC with the one corresponding to
“4A16PSK PCM2” in DSTBC for a mobile terminal
velocity of 100 km/h is compared. There, it can be ob-
served that the improvement for “4A16PSK PCM2”
is approx. 4.82 dB at BER = 1x10
−1
.
In Fig. 3 the results obtained for the refer-
ence system (64-PSK in DSTBC) and for “4A16PSK
PCM2”, when the mobile terminal velocity is 150
km/h, are shown. As it can be observed in Fig. 3,
Table 1: Simulation parameters.
Parameter Value
Carrier Frequency f
c
= 5 GHz
Bandwidth B = 10 MHz
Number of subcarriers N
FFT
= 128
Subcarrier spacing ∆f =
B
N
FFT
= 78125 Hz
Symbol Duration T
s
= 12.8 µs
Guard interval T
G
=
T
s
8
= 1.6 µs
Symbol interval T
S+G
= T
s
+ T
G
= 14.4 µs
Number of paths P = 30
Number of clusters (groups of paths) N
c
= 1
Maximum time delay τ
max
= 1 µs
Mobile velocity v = 5, 50, 100,150,200,300 km/h
Maximum Doppler shift f
Dmax
= f
0
·
v
c
≈ 23,231, 463, 694, 926,1389 Hz
using f
0
= f
c
Time Delay distribution b =
τ
max
ln(1000)
= 0.1448 µs
15 20 25 30 35
10
−4
10
−3
10
−2
10
−1
10
0
SNR [dB]
BER
64−PSK average
4A16PSK PCM2 realizations
4A16PSK PCM2 average
Figure 2: Performance of “4A16PSK PCM2” used in
DSTBC under WSSUS channels (H
k
≈ H
k−1
,v = 100
km/h).
the degradation due to the velocity increment is not
equal for both systems, being higher for the first one.
That increases the improvement obtained by using
“4A16PSK PCM2” instead of 64-PSK in DSTBC; it
is approx. 5.71 dB at BER = 1x10
−1
for this case.
In Fig. 4 the performance for 64-PSK in DSTBC
and “4A16PSK PCM2” in DSTBC were evaluated
for a mobile terminal velocity of 200 km/h. By
comparing the average results for both techniques,
an improvement of 6.65 dB at BER = 1x10
−1
for
“4A16PSK PCM2” technique is obtained. For 005
km/h, 050 km/h and 300 km/h, the improvements are
4.73 dB, 4.76 dB and 14.06 dB respectively. That
means that the improvement is significantly increased
with the increment of the mobile terminal velocity. It
DifferentialSpaceTimeBlockCodesforHighMobilityScenarios
379

15 20 25 30 35
10
−3
10
−2
10
−1
10
0
SNR [dB]
BER
64−PSK average
4A16PSK PCM2 realizations
4A16PSK PCM2 average
Figure 3: Performance of “4A16PSK PCM2” used in
DSTBC under WSSUS channels (H
k
≈ H
k−1
,v = 150
km/h).
shows that “4A16PSK PCM2” is particularly conve-
nient for high mobility scenarios.
15 20 25 30 35
10
−3
10
−2
10
−1
10
0
SNR [dB]
BER
64−PSK average
4A16PSK PCM2 realizations
4A16PSK PCM2 average
Figure 4: Performance of “4A16PSK PCM2” used in
DSTBC under WSSUS channels (H
k
≈ H
k−1
,v = 200
km/h).
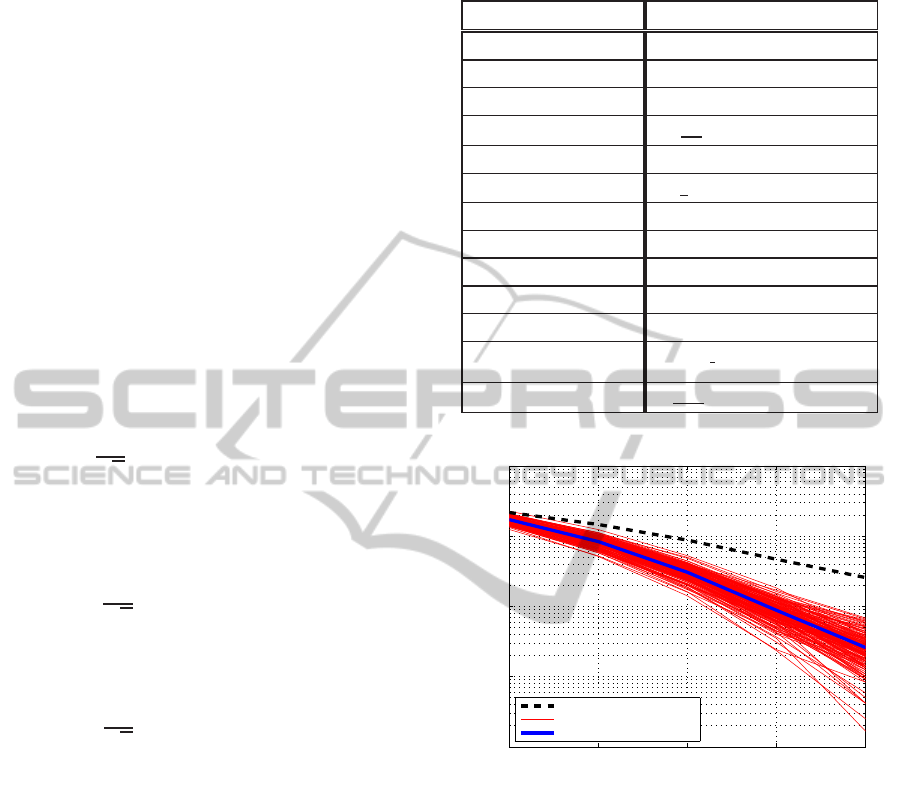
In Fig. 5 the variation of the improvement for
“4A16PSK PCM2” with the velocity of the mobile
terminal is summarized. Observe that the previ-
ous discussion is about the improvement in perfor-
mance of “4A16PSK PCM2” with respect to 64-PSK
in DSTBC, not about the absolute performance of
“4A16PSK PCM2”. For sure it diminishes when the
velocity of the mobile terminal is increased; but it di-
minishes less than for 64-PSK in DSTBC.
4 CONCLUSIONS
In this paper the performance of a new technique re-
ported in (Rodr´ıguez and Rohling, 2006) is analyzed
0 50 100 150 200 250 300
0
5
10
15
Mobile terminal velocity [km/h]
Improvement respect to 64−PSK in DSTBC [dB]
Figure 5: Relative improvement of “4A16PSK PCM2” with
respect to 64-PSK -used in DSTBC- versus mobile terminal
velocity, under WSSUS channels (H
k
≈ H
k−1
).
for different mobile terminal velocities. The results
show that this technique is particularly convenient for
high mobility scenarios. It is also known that this in-
teresting characteristic is also shared, at least, by other
APSK technique (“2L-APSK”) (Vanaev and Rohling,
2006), (Rodr´ıguez, 2007).
In (Rodr´ıguez and Rohling, 2007) the improve-
ment obtained for “4A16PSK PCM2” by using re-
ceive diversity is reported, which is a simple alterna-
tive to improve the performance of this technique.
It is important to note the low system complexity
of “4A16PSK PCM2’ used in DSTBCs, even when
receive diversity is used.
Finally, it is also important to highlight the advan-
tages of OFDM, MIMO and DSTBC associated to
this technique. By being applicable to OFDM tech-
niques, the robustness in multipath fading scenarios
is assured. By being a MIMO technique, better band-
width efficiency can be achieved, and as a differen-
tial modulation technique a low computational com-
plexity can be maintained. As a summary, this is a
technique with very high potential for high mobility
scenarios.
REFERENCES
Alamouti, S. M. (1998). A simple transmit diversity tech-
nique for wireless communications. IEEE Journal on
Selected Areas in Communications, 16(8):1451–1458.
Bauch, G. (2004). Differential amplitude and unitary space-
time modulation. In Proc. of the 5
th
International ITG
Conference on Source and Channel Coding, Erlangen,
Germany.
Bauch, G. and Mengi, A. (2005). Non-unitary orthogonal
differential space-time modulation with non-coherent
WINSYS2012-InternationalConferenceonWirelessInformationNetworksandSystems
380

soft-output detection. In Proc. of the IEEE 62
nd
Ve-
hicular Technology Conference (VTC’05-Fall), Dal-
las, USA.
Chen, Z., Zhu, G., Shen, J., and Liu, Y. (2003). Differential
space-time block codes from amicable orthogonal de-
signs. In Proc. of the IEEE Wireless Communications.
Fellenberg, C. and Rohling, H. (2009). Quadrature am-
plitude modulation for differential space-time block
codes. Wireless Personal Communications, 50:247–
255.
Hoeher, P. (1992). A statistical discrete-time model for the
WSSUS multipath channel. IEEE Transactions on Ve-
hicular Technology, 41(4):461–468.
Hwang, C.-S., Nam, S.H., Chung, J., and Tarokh, V. (2003).
Differential space-time block codes using nonconstant
modulus constellations. IEEE Transactions on Signal
Processing, 51(11).
Jiang, T., Song, L., and Zhang, Y. (2010). Orthogonal Fre-
quency Division Multiple Access Fundamentals and
Applications. CRC Press, Taylor and Francis, Florida,
USA.
Rodr´ıguez, B. (2007). Differential STBC for OFDM based
Wireless Systems. PhD thesis, Technische Universit¨at
Hamburg-Harburg (TUHH), Department of Telecom-
munications.
Rodr´ıguez, B. and Rohling, H. (2006). A new class of
differential space time block codes. In Proc. of the
11
th
International OFDM-Workshop, pages 106–110,
Hamburg, Germany.
Rodr´ıguez, B. and Rohling, H. (2007). Receive diversity in
DSTBC using APSK modulation schemes. In Proc. of
the 12
nd
International OFDM-Workshop, pages 90–
94, Hamburg, Germany.
Tao, M. and Cheng, R. S. (2001). Differential space-time
block codes. In Proc. of the IEEE Globecom.
Tarokh, V. and Jafarkhani, H. (2000). A differential detec-
tion scheme for transmit diversity. IEEE Journal on
Selected Areas in Communications, 18:1169–1174.
Tarokh, V., Jafarkhani, H., and Calderbank, A. (1999).
Space-time block codes from orthogonal designs.
IEEE Transactions on Information Theory, 45:1456–
1467.
Vanaev, A. and Rohling, H. (2006). Design of amplitude
and phase modulated signals for differential space-
time block codes. Wireless Personal Communications,
39(4):401–413.
Xia, X.-G. (2002). Differentially en/decoded orthogonal
space-time block codes with APSK signals. IEEE
Communications Letters, 6:150–152.
DifferentialSpaceTimeBlockCodesforHighMobilityScenarios
381